基于启发式算法的生物机器人成本优化问题

Cost Optimization Problem of Biorobot Based on Heuristic Algorithm

摘要: 随着微机电科技的发展，血管机器人被研发出来用于携带药物放入血管里定点治疗与血管有关的疾病，还可以充当血管清道夫，清除病毒，保持人体健康。因而血管机器人的研究和发展越来越受到人们的关注。本研究结合启发式贪心算法与粒子群算法，以血管机器人购买和保养成本为目标函数，考虑实际每周血管机器人需求数量，提出约束条件，建立机器人购买优化模型。结果显示，结合贪心算法和粒子群算法相比于传统求解寻优能力有了较高的提升，效率更高，结果更准确，适用于血管机器人成本优化问题。

Abstract: With the development of micro-electromechanical technology, vascular robots have been developed to carry drugs into blood vessels to treat vascular-related diseases. They can also act as vascular scavengers, remove viruses, and maintain human health. Therefore, the research and development of vascular robots have attracted more and more attention. This study combines heuristic greedy algorithm and particle swarm optimization algorithm, takes the purchase and maintenance cost of vascular robots as the objective function, considers the actual weekly demand for vascular robots, proposes constraints, and establishes a robot purchase optimization model. The results show that the combination of greedy algorithm and particle swarm optimization algorithm has a higher improvement than the traditional solution optimization ability, higher efficiency, more accurate results, and is suitable for the cost optimization problem of vascular robots.

1. 引言

随着微机电系统的发展，人类制造出的血管机器人可以携带药物放入血管里定点治疗与血管有关的疾病，还可以充当血管清道夫，清除病毒，保持人体健康。目前学界内对血管内运动机器人研究目前大致可以分成两个方向：一是微观生物机器人，该类课题隶属生命科学工程研究范畴，例如美国哥伦比亚大学科学家研制出的一种“纳米蜘蛛”机器人。二是仿生微小型管道机器人。生物具有人工机械无法比拟的优越性能，因此仿生学一直为科学家研究的热点。血管介入机器人就是仿生微小型管道机器人，其实质是外科手术机器人与血管介入技术的有机结合。机器人操纵介入手术器械，它可以工作在对医生不利的环境，参照医疗图像精确定位，能够没有颤动地执行持续动作，同时快速、准确地通过复杂的轨迹，精确定位到达目标血管，最后在医生的指挥下或自主地完成血管介入手术。

虽然现有的微型机器人技术相对成熟，通过微型机器人进行血管治疗的临床效果显著提高，但是昂贵的价格让部分医院难以承受。为了让更多的医院可以掌握此项技术，通过调度研究以最小的成本实现血管内运动机器人的技术扩充和临床实践，解决部分医院机器人使用最优化成本问题 [1] [2] 。

2. 微型机器人购买最优策略分析

本研究以某医院血管机器人的订购与生物学习为例，医院使用的是ABLVR型号的血管机器人。目前ABLVR的机械结构可以由两个部分组成，分别是容器艇(操作组件一)有动力，可在血液中游动，与操作手(操作组件二)有生物大脑和机械臂，生物大脑控制着机械臂进行工作，操作手可以从容器艇上拆卸、安装、更换。血管机器人在患者血管中工作时间为一周，在完成相应的医疗任务之后必须取出。

ABLVR微型机器人的投入使用需要满足一定的条件，首先每个容器艇四周安装4个操作手以实现临床操作，这就要求在进行ABLVR微型机器人的投入和使用时要按照现有可用的操作部件进行预购决策在满足临床操作的同时尽可能压缩使用成本。

表1与表2给出医院104周血管机器人的需求数量以及相关的使用成本。

ABLVR机器人的使用需要遵循使用环境标准，机器人在每次完成工作后，容器艇(操作组件一)与操作手(操作组件二)必须拆卸进行相应的保养和维护。取出后的容器艇(操作组件一)不必须要保养，可以连续使用，但如果没有使用则需要进行保养；操作手(操作组件二)在取出后必须进行保养才能再次开展工作，保养时间为一周。

Table 1. Vascular robot demand quantity table

表1. 血管机器人需求数量表

Table 2. Costs associated with the use of vascular robots

表2. 血管机器人相关使用成本

血管机器人在投入使用前需要进行特定的生物学习，由于没有直接的信息复制功能，新购买的操作手在工作之前需要提前进行训练，类似于人脑学习，训练的过程需要在特定的环境中由已经学习好的操作手(熟练工)“指导”若干个生物大脑芯片空白的操作手(新手)在仿真血管中进行学习，直到“新手”能够达到“熟练工”的水平为止，每个熟练操作手可以作为指导者“指导”10个购买的新操作手进行生物学习，时间为一周。

2.1. 目标函数与约束条件

通过已知的条件，对研究问题进行梳理。目标问题是使用条件下的微型机器人最优购买决策问题，针对于最优化问题，本节采用贪心算法求解。经典贪心算法 [3] 求解过程需要建立数学模型描述问题，把求解的问题分成若干子问题，对每个子问题进行求解，得到子问题的局部最优解，最后把子问题的局部最优解合成原问题的一个可行解 [4] ，进而得到全局最优解。机器人需求数量柱状图如图1所示。

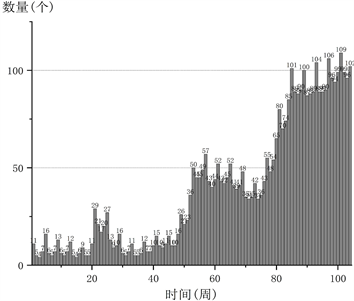
Figure 1. Bar chart of the number of robots required

图1. 机器人需求数量柱状图

为了更好地约束最优问题的目标函数范围，本次研究针对最小化成本函数添加启发式算法，由容器艇和操作手的工作机制可知，刚购买的容器艇需要一周时间调试，刚购买的操作手也需要一周时间学习，基于贪心算法，每周开始时恰好购买下一周需要使用和这周正在休息的差值即可。

2.1.1. 操作组件一相关求解过程

基于局部最优解为全局最优解的考量，根据容器艇购买情况建立模型。可以得到如下目标函数，相关符号见附表1：

$\min \left({\displaystyle \underset{i=1}{\overset{7}{\sum }}\left(b_{ci}\cdot 200+\left({\displaystyle \underset{k=0}{\overset{i}{\sum }}{b}_{ck}+13-w_{ci+1}}\right)\cdot 10\right)}\right),i=1,2,\cdots ,8$ (1)

约束条件s.t.

${\displaystyle \underset{k=0}{\overset{i}{\sum }}{b}_{ck}}+13\ge w_{ci+1},i=1,2,\cdots ,8$ (2)

显然通过以上公式可以得到其计算过程，将M_ci−1 + W_ci−1与W_ci的值进行比较，可以得到：

$\begin{array}{l}\text{if}{M}_{ci-1}+W_{ci-1}\ge W_{ci}则B_{ci-1}=0,M_{ci}=M_{ci-1}+W_{ci-1}-W_{ci}\\ \text{if}{M}_{ci-1}+W_{ci-1}<W_{ci}则B_{ci-1}=W_{ci}-\left(M_{ci-1}+W_{ci-1}\right)\end{array}$

2.1.2. 操作组件二相关求解过程

同理基于局部最优解为全局最优解的考量，根据机器手部件购买情况建立模型。得到如下目标函数，相关符号见附表1：

$\min \left({\displaystyle \underset{i=1}{\overset{7}{\sum }}\left(b_{hi}\cdot 100+5\left(50+{\displaystyle \underset{k=0}{\overset{i}{\sum }}{b}_{hk}-w_{hi}-\lceil b_{hi}/10\rceil }\right)+10\left(b_{hi}+\lceil b_{hi}/10\rceil \right)\right)}\right),i=1,2,\cdots ,8$ (3)

约束条件s.t.

$50+{\displaystyle \underset{k=0}{\overset{i}{\sum }}{b}_{hk}-w_{hi}}\ge w_{hi+1},i=1,2,\cdots ,8$ (4)

其中 $\lceil \rceil$ 代表向上取整符号。对以上公式整理可以得到其计算过程，将M_hi−1与W_hi值进行比较，同时考虑到W_hi+1与M_hi的大小可以得到如下四种情况，分别进行讨论得到：

$\text{if}{M}_{hi-1}\ge W_{hi}\text{and}{W}_{hi+1}\le M_{hi}则\{\begin{array}{l}{M}_{hi}=M_{hi-1}-W_{hi}+W_{hi-1}\hfill \\ B_{hi}=0\hfill \\ P_{hi}=0\hfill \\ M_{hi+1}=W_{hi}+M_{hi}-W_{hi+1}\hfill \\ M{M}_{hi+1}=M_{hi}-P_{hi}\hfill \end{array}$

$\text{if}{M}_{hi-1}\ge W_{hi}\text{and}{W}_{hi+1}>M_{hi}则\{\begin{array}{l}{M}_{hi}=M_{hi-1}-W_{hi}+W_{hi-1}\hfill \\ B_{hi}=W_{hi+1}-M_{hi}\hfill \\ P_{hi}=ceiling\left(\left(W_{hi+1}-M_{hi}\right)/10\right)\hfill \\ M_{hi+1}=W_{hi}\hfill \\ M{M}_{hi+1}=M_{hi}-P_{hi}\hfill \end{array}$

$\text{if}{M}_{hi-1}<W_{hi}\text{and}{W}_{hi+1}\le M_{hi}则\{\begin{array}{l}{B}_{hi}=0\hfill \\ P_{hi}=0\hfill \\ M_{hi+1}=W_{hi}+M_{hi}-W_{hi+1}\hfill \\ M{M}_{hi+1}=M_{hi}-P_{hi}\hfill \\ B_{hi-1}=W_{hi}-M_{hi-1}\hfill \\ P_{hi-1}=ceiling\left(\left(W_{hi}-M_{hi-1}\right)/10\right)\hfill \\ M_{hi}=W_{hi}-1\hfill \\ M{M}_{hi-1}=M_{hi-1}-P_{hi-1}\hfill \end{array}$

$\text{if}{M}_{hi-1}<W_{hi}\text{and}{W}_{hi+1}>M_{hi}则\{\begin{array}{l}{B}_{hi}=W_{hi+1}-M_{hi}\hfill \\ P_{hi}=ceiling\left(\left(W_{hi+1}-M_{hi}\right)/10\right)\hfill \\ M{M}_{hi}=M_{hi}-P_{hi}\hfill \\ B_{hi-1}=W_{hi}-M_{hi-1}\hfill \\ P_{hi-1}=ceiling\left(\left(W_{hi}-M_{hi-1}\right)/10\right)\hfill \\ M_{hi}=W_{hi}-1\hfill \\ M{M}_{hi-1}=M_{hi-1}-P_{hi-1}\hfill \end{array}$

2.2. 结果分析

根据上述目标函数求解局部最优，再通过局部最优得到全局最优后的结果分析，可以得到操作部件一与操作部件二在104周的需求数量。其中需要的操作部件一数量与需要的操作部件二数量如图2所示。

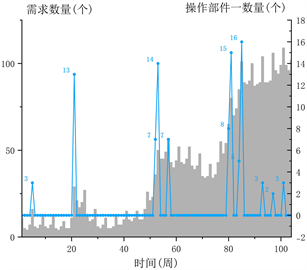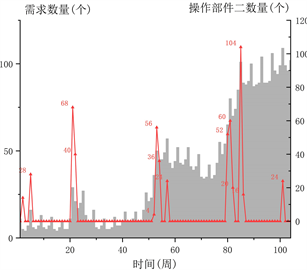(a) (b)

Figure 2. Required number of operating components

图2. 操作部件需求数量

从图2中的结果来看需求数量的增加分别在第5周、第21周、第52周、第80周、第101周左右开始，操作组件一与操作组件二在最小化成本的目标下得到具体的需求数据。

Table 3. 1~8 week usage and cost of container boats

表3. 1~8周容器艇使用情况和成本费用

Table 4. 1~8 week usage and cost of operators

表4. 1~8周操作手使用情况和成本费用

尽管两个操作部件在保养限制条件、训练限制条件上有所不同，从图3中的操作部件需求趋势曲线中可以明显看到尽管在数量上的增量没有一致，操作部件一与操作部件二却有着相同的变化趋势，医院微型机器人的在一周内增加的数量越多，影响预计操作部件购买数量越大，可以看到在表3和表4中，操作手的需求数量远大于容器艇，在这种情况下操作手购买成本与训练保养成本都是远高于容器艇的购买成本与保养成本。

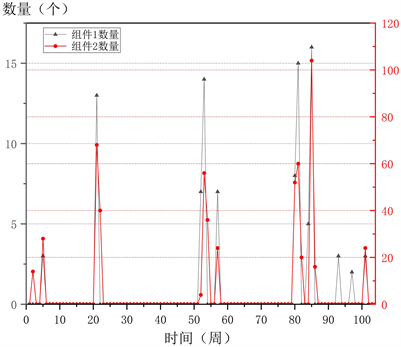
Figure 3. Trend diagram of different components purchase quantity

图3. 不同组件购买数量趋势图

以上结果表明在在保养限制条件、训练限制条件下，通过启发式的贪心算法可以得到容器艇和操作手的购买数量以及成本费用，在有限的限制条件下通过启发式的贪心算法计算出局部最优解从而得到全局最优解，最优目标函数的值分别是78,510元和292,620元。

3. 多条件限制下的购买决策分析

本节在上述购买条件下加入多个条件，其中改变章节2中每个熟练操作手可以作为指导者“指导”10个购买的新操作手进行生物学习的假设条件，另为每个熟练操作手可以作为指导者“指导”不超过20个购买的新操作手进行生物学习。根据相关内容，血管机器人在患者血管中工作有风险，一旦碰上巨噬细胞，如果躲避不及，将会完全损毁，所以在本节加入限制条件假设每周有10%的血管机器人损毁(损毁的个数按四舍五入取整)。

同时假设医院在购买容器艇与操作手时有优惠政策。即容器艇一次性购买量不超过5个时的单价为200元/个；容器艇一次性购买量超过5个但不超过10个时，超过5个的那部分单价为180元/个；容器艇一次性购买量超过10个时，超过10个的那部分单价为160元/个。同样，操作手一次性购买量不超过20个时的单价为100元/个；操作手一次性购买量超过20个但不超过40个时，超过20个的那部分单价为90元/个；操作手一次性购买量超过40个时，超过40个的那部分单价为80元/个。

3.1. 研究方法

加入上述假设后虽然限制条件增多，但原有的最优化问题由过去的贪心算法可寻最优解变为在全局最优解的情况下并不一定是每一步的局部最优解，求出每一步的局部最优并不能得到最终的全局最优，在此情况下，为了得到全局最优解，针对本问题采用了启发式的粒子群算法，通过每一步的启发式最优解，进行粒子群搜索，进而得到最后的全局最优解。

3.1.1. 启发式算法相关目标函数与约束条件

根据本节假设条件建立多条件限制下的目标函数，可以得到：

$\min \left({\displaystyle \underset{i=1}{\overset{104}{\sum }}\left(A+5\cdot \left(13+{\displaystyle \underset{k=1}{\overset{i}{\sum }}{b}_{ck}-w_{ci}-round\left(0.1\cdot {\displaystyle \underset{k=1}{\overset{i}{\sum }}{w}_{ck}}\right)}\right)\right)}\right),i=1,2,\cdots ,104$ (5)

$\min \left({\displaystyle \underset{i=1}{\overset{104}{\sum }}\left(B+10\cdot \left(b_{hi}+\lceil b_{hi}/20\rceil \right)+5\cdot \left(50+{\displaystyle \underset{k=1}{\overset{i}{\sum }}{b}_{hk}-w_{hi+1}-4\cdot round\left(0.1\cdot {\displaystyle \underset{k=1}{\overset{i}{\sum }}{w}_{ck}}\right)}-\lceil b_{hi}/20\rceil \right)\right)}\right),i=1,2,\cdots ,104$ (6)

其中A、B分别表示：

$I_{b_{ci}\le 5}\cdot 200\cdot b_{ci}+I_{5<b_{ci}\le 10}\cdot \left[b_{ci}\cdot 180+100\right]+I_{10<b_{ci}}\cdot \left[b_{ci}\cdot 160+300\right]$ (7)

$I_{b_{hi}\le 20}\cdot 100\cdot b_{hi}+I_{20<b_{hi}\le 40}\cdot \left[b_{hi}\cdot 90+200\right]+I_{10<b_{hi}}\cdot \left[b_{hi}\cdot 80+600\right]$ (8)

约束条件s.t.

$13+{\displaystyle \underset{k=1}{\overset{i}{\sum }}{b}_{ck}}-round\left(0.1\cdot {\displaystyle \underset{k=1}{\overset{i}{\sum }}{w}_{ck}}\right)\ge w_{ci+1},i=1,2,\cdots ,104$ (9)

$50+{\displaystyle \underset{k=1}{\overset{i}{\sum }}{b}_{hk}}-round\left(w_{ci}\cdot 0.9\right)\cdot 4-4\cdot round\left(0.1\cdot {\displaystyle \underset{k=1}{\overset{i}{\sum }}{w}_{ck}}\right)\ge w_{hi+1},i=1,2,\cdots ,104$ (10)

3.1.2. 粒子群算法

粒子群算法 [5] [6] (PSO: Particle swarm optimization)通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。

本次研究采用的粒子群算法是经过改良后的粒子群算法 [7] ，针对不同周的情况不同给定了粒子群的可移动范围缩小了整体的搜索环境，同时给定范围的边界值，表5展示了改进PSO的各项参数设置。虽然在前期生成粒子群的计算过程较为繁琐，但改进后粒子在边界值与局部最优值之间进行搜索，确保粒子群寻找最优结果的有效性 [8] 。为了加快粒子群的搜索速度，初始化参数时，粒子群的步长以改进的对数函数进行收敛，这种改进方法将打打提高模型的收敛速度，得到最终结果。

Table 5. Improved PSO parameter table

表5. 改进PSO参数表

3.1.3. 对需求序列的分析与预测

在这一小节中，运用经典的时间序列分析方法，对医院微型机器人需求序列进行分析，通过已知的数据，采用ARIMA模型进行预测。考虑到数据个数与性质，对需求序列数据采用单位根检验。

Table 6. Unit root test of time series data

表6. 时间序列数据单位根检验

由表6可知，P值大于0.05，说明接受原假设，时间序列不平稳。为了序列平稳，对数据进行一阶差分，差分后的数据由图4所示。

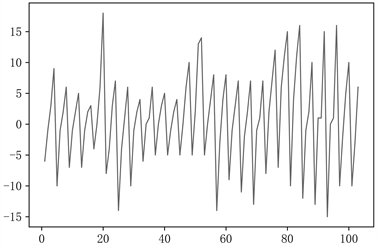
Figure 4. First-order difference data diagram

图4. 一阶差分数据图

可见一阶差分后的数据波动近似于白噪声，均值趋近于0并且方差无异常，符合时间序列的预测假设，根据以上结果，实验在一阶差分的基础上进行时间序列的预测，通过对比不同参数下ARIMA模型的拟合参数值，得到最优的预测模型为ARIMA(5, 1, 0)，利用ARIMA(5, 1, 0)拟合曲线得到最终的预测结果如表7和图5。

Table 7. Demand sequence prediction results

表7. 需求序列预测结果

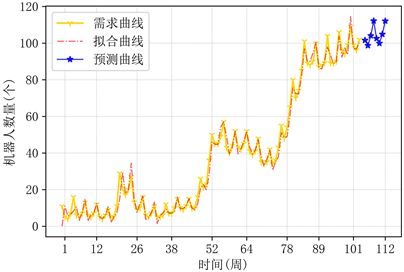
Figure 5. Vascular robot demand prediction curve

图5. 血管机器人需求预测曲线

通过对比图可以得到需求的预测曲线与拟合曲线基本一致，模型的预测效果达到了理想的结果。

3.2. 结果分析

根据粒子群算法迭代后的结果，得到图6。可以看到相比较第二节结果，由于每一周在进行血管治疗的机器人都有百分比的损耗，随着时间的增加，购买的数量也在逐步增在，原本在无机器损耗的情况下可以不进行购买的时间段，也要对血管机器人做到必要的补充，弥补消耗带来的损失。在这种情况下，保养的数量相比较上节结果有所减少，对应的保养总成本减少，补充购买机器人却使得成本相比较无损耗的情况下大幅增加。

分别对两个组件满足需求的情况下做出相应的成本累积柱状图，图7中的结果表明成本的主要部分来自组件一的成本，初始阶段总成本曲线相当比较平稳，在50周后，成本曲线的上下波动较大，主要是因为在机器人有损耗的情况下，过多的需求量将影响下一周的机器人补充购买数量，相应的增加了下一周的购买成本与训练成本。最终组件一成本目标函数值为96,830元，组件二成本目标函数值为334,095元。

4. 结论

本文针对某医院现有的血管机器人需求问题，在最小化成本函数的目标下，运用了启发式的贪心算法，根据现有的需求条件将多步局部最优解组合为全局最优解，通过计算得到全局最优解，有效解决了

Figure 6. Comparison of purchase quantity and maintenance quantity

图6. 购买数量与保养数量结果对比图

Figure 7. Bar chart of component costs

图7. 组件成本柱状图

现有相关背景下医院对血管机器人购买的最优化问题。在此基础上，利用ARIMA模型预测了需求曲线，加入血管机器人损耗条件与购买优惠政策，利用启发式的粒子群算法寻找到全局最优解，提供相应的最优决策。

基金项目

国家自然科学基金地区基金(72261004)；贵州省科技重大专项计划(20183002)。

附录

Table S1. Symbol description

附表1. 符号说明

NOTES

^*通讯作者。