基于箝位矩阵的公钥密码

Public Key Cryptography Based on Clamping Matrix

摘要: 箝位矩阵是一类以一定范围内的非负整数作为构成元素的矩阵，且在运算过程中这些元素始终被钳制在该范围内。构造两组在箝位运算下互逆的方阵，由此生成一对密钥。在一阶矩阵情形下，箝位设计的密码系统只具多项式复杂度的破解强度，当二阶以上时，原先的破解成因不复存在，从而陡然升级为NP复杂度的强度，且随着矩阵阶数的增大而呈指数增强。箝位矩阵的公钥密码具有独特的批处理加解密形式，虽然涉及矩阵乘法，但对每个明文处理单位而言，平均计算占有并不高。和传统的RSA、Elgamal和椭圆密码等基于大素数（或基于由大素数参与构造的有限域）不同，箝位矩阵的公钥密码的密钥获取极其容易，不需要耗费资源作素数检验，而且箝位矩阵的公钥密码系统具有自然的随机性效应，不像RSA需要专门设计的附加随机填充的模式，或者不像Elgamal引入临时性的随机密钥那样的协议交互的设计。由此可以证明，箝位矩阵密码系统具有像离散对数困难性那样的归约到枚举未定矩阵形式的NP复杂度强度。

Abstract: Clamping matrix was a kind of matrix whose elements were non-negative integers within a certain range, and these elements were always clamped within this range during the operation. Be constructed to two sets of square matrices that were mutually inverse under the clamp operation, thereby generating a pair of keys. In the case of a first-order matrix, the clamp-designed cryptosys-tem only had the cracking strength of polynomial complexity. When it was higher than the second order, the original cracking causes no longer exists, so it was suddenly upgraded to the strength of NP-complexity, and with the matrix, it increased exponentially as the order increases. The public key cryptography of the clamping matrix had a unique form of batch encryption and decryption. Although matrix multiplication was involved, the average computational occupancy for each plaintext processing unit was not high. Different from traditional RSA, Elgamal and elliptic ciphers based on large prime numbers (or based on finite fields constructed by large prime numbers), the key acquisition of public key cryptography with a clamping matrix was extremely easy, and it did not need to spend resources for prime number checking. Moreover, the public key cryptosystem of the clamping matrix had a natural randomness effect, unlike RSA which required a specially designed pattern of additional random padding, or the design of protocol interaction like Elgamal introduced a temporary random key. Clamping-matrix cryptosystems could be shown to have NP-complexity strengths like discrete log difficulty reduction to enumerated indeterminate matrix form.

1. 问题背景

经典的非对称密钥系统RSA (Rivest-Shamir-Adleman)、Elgamal和椭圆密码 [1] [2] [3] [4] [5] 是基于大素数来构造的：例如RSA是通过两个大素数相乘获得一个半素数，通过基于半素数的欧拉数的同余运算构造一对互逆指数实现加解密运算；Elgamal是使用一个大素数构造的有限域上的循环群的离散对数计算困难性实现保密机制；椭圆密码则是利用有限域上的椭圆曲线的点加运算实现加解密，本质上还是一类离散对数计算困难性问题，相对于一般有限域循环群的离散对数问题，椭圆密钥构造需要的素数可以更小一些。

以上算法的构造无一例外都需要大素数的支持，而大素数是稀缺资源，寻找合适的大素数是和素数检验有密切的关系的。Miller-Rabin素数检验是概率素数检验，一种确定给定数是否可能为素数的算法 [6] [7] [8] 。可见，这些算法的应用在安全性较高的前提下，其本身的密钥生成的不易程度也是一个制约因素。此外，这些密码系统都是基于数域可交换运算来实现的，对未来量子计算而言，具有一定的无法抵御攻击的风险。专利 [9] 是一类基于箝位矩阵结构而设计的非对称密码，专利阐述了该方法的步骤并给出应用的示例。本文分析该专利的公钥密码系统的原理和安全性，以及数值实验比较，它突出的特点是密钥生成极其简单，另外，由于矩阵乘法的不可交换性，对于抵御未来量子计算攻击也是具一定的趋好因素。

后文首先介绍该密钥的设计原理和加解密模式，然后再证明密钥的安全性，最后是加解密数据实验。

2. 密钥设计原理

引入记号 $z_N{z}_{N-1}\cdots z_2{z}_1$ 表示一N位的整数，其中 $z_i$ 为 $0,1,2,\cdots ,9$ ( $\forall 1\le i\le N$ )的任意数字，即

$z_N{z}_{N-1}\cdots z_2{z}_1={\displaystyle \underset{i=1}{\overset{N-1}{\sum }}{z}_i\cdot {10}^{i-1}}$ (1)

对任意 $1\le 2k+1\le N$ 显然有拆分 $z_N{z}_{N-1}\cdots z_2{z}_1=z_N{z}_{N-1}\cdots z_{2k+2}\cdot {10}^{2k+1}+z_{2k+\text{1}}{z}_{\text{2}k}\cdots z_2{z}_1$ (对 $2k+1=N$ ，有 $z_N{z}_{N-1}\cdots z_{2k+2}=0$ )。再定义取该整数末2k + 1位数的箝位运算，即 $\underset{\_}{z_N{z}_{N-1}\cdots z_2{z}_1}=z_{\text{2}k+1}{z}_{2k}\cdots z_2{z}_1$ (k为任意大于等于零的整数)，参数2k + 1为箝位指数。下面先从整数开始探讨箝位运算的一些性质，最后引申到矩阵也具备这些箝位特点。

引理1. 设正整数a，b，k，则高斯取整函数满足性质 $\left[\frac{a\cdot b}{{\text{10}}^k}\right]\ge \left[\frac{a}{{\text{10}}^k}\right]\cdot b$ 。

证明：设 $a={\displaystyle \underset{i=0}{\overset{N}{\sum }}{a}_i}\cdot {10}^i$ , $b={\displaystyle \underset{i=0}{\overset{M}{\sum }}{b}_i}\cdot {10}^i$ 其中N、M为非负整数，于是 $a\cdot b={\displaystyle \underset{i+j=0}{\overset{i+j=N+M}{\sum }}\left(a_i{b}_j\right){10}^{i+j}}$ ， $\left[\frac{a\cdot b}{{\text{10}}^k}\right]={\displaystyle \underset{i+j=k}{\overset{i+j=N+M}{\sum }}\left(a_i{b}_j\right){10}^{i+j-k}}$ 。而 $\left[\frac{a}{{\text{10}}^k}\right]\cdot b={\displaystyle \underset{i=k}{\overset{N}{\sum }}{a}_i}\cdot {10}^{i-k}\cdot {\displaystyle \underset{i=0}{\overset{M}{\sum }}{b}_i}\cdot {10}^i={\displaystyle \underset{i\ge k,i+j=k}{\overset{i+j=N+M}{\sum }}\left(a_i{b}_j\right){10}^{i+j-k}}$ 。对于每个固定的幂次 $i+j-k$ ，均有 ${\displaystyle \underset{i+j\ge k}{\sum }{a}_i{b}_j}\ge {\displaystyle \underset{i\ge k}{\sum }{a}_i{b}_j}$ (因为 $i\ge k\Rightarrow i+j\ge k$ 故右边的组合选项数少于左边)，例如对于 $i+j-k=\text{2}$ ，左边为 $\left(a_0{b}_{k+2}+\cdots +a_k{b}_2+a_{k+1}{b}_1+a_{k+2}{b}_0\right)$ ，右边为 $\left(a_k{b}_2+a_{k+1}{b}_1+a_{k+2}{b}_0\right)$ 。故 $\left[\frac{a\cdot b}{{\text{10}}^k}\right]\ge \left[\frac{a}{{\text{10}}^k}\right]\cdot b$ 。

引理2. 低位保持原理。设整数u、v、a的乘积为N位整数，u、a乘积为M位整数，v、a乘积为T位整数，即

$uva=z_N{z}_{N-1}\cdots z_2{z}_1$ (2)

$ua=x_M{x}_{M-1}\cdots x_2{x}_1$ (3)

$va=y_T{y}_{T-1}\cdots y_2{y}_1$ (4)

并且 $N\ge 2k+1$ ， $M\ge 2k+1$ 以及 $M\ge 2k+1$ ，k为某确定的正整数。则有

$\underset{\_}{uva}=\underset{\_}{\underset{\_}{ua}v}=\underset{\_}{\underset{\_}{va}u}$ (5)

证明：首先由式(2)得

$\underset{\_}{uva}=z_{\text{2}k+1}{z}_{2k}\cdots z_2{z}_1$ (6)

由式(3)得到

$\underset{\_}{ua}=x_{2k+1}{x}_{2k}\cdots x_2{x}_1$ (7)

于是

$\begin{array}{c}\underset{\_}{ua}v=x_{2k+1}{x}_{2k}\cdots x_2{x}_1\cdot v\\ =\left(x_M{x}_M\cdots x_{2k+\text{2}}{x}_{2k+1}{x}_{2k}\cdots x_2{x}_1-x_M{x}_M\cdots x_{2k+\text{2}}\cdot {10}^{2k+1}\right)\cdot v\\ =x_M{x}_M\cdots x_{2k+\text{2}}{x}_{2k+1}{x}_{2k}\cdots x_2{x}_1\cdot v-x_M{x}_M\cdots x_{2k+\text{2}}\cdot {10}^{2k+1}\cdot v\\ =uav-x_M{x}_M\cdots x_{2k+\text{2}}\cdot {10}^{2k+1}\cdot v\\ =z_N{z}_{N-1}\cdots z_2{z}_1-x_M{x}_M\cdots x_{2k+\text{2}}\cdot {10}^{2k+1}\cdot v\\ =z_N{z}_{N-1}\cdots z_{2k+3}{z}_{2k+2}\cdot {10}^{2k+1}+z_{2k+1}{z}_{2k}\cdots z_2{z}_1-x_M{x}_M\cdots x_{2k+\text{2}}\cdot {10}^{2k+1}\cdot v\\ =\left(z_N{z}_{N-1}\cdots z_{2k+3}{z}_{2k+2}-x_M{x}_M\cdots x_{2k+\text{2}}\cdot v\right)\cdot {10}^{2k+1}+z_{2k+1}{z}_{2k}\cdots z_2{z}_1\end{array}$

又根据引理1得

$z_N{z}_{N-1}\cdots z_{2k+3}{z}_{2k+2}=\left[\frac{uav}{{10}^{2k+1}}\right]\ge \left[\frac{ua}{{10}^{2k+1}}\right]v=x_M{x}_M\cdots x_{2k+\text{2}}\cdot v$

即式中 $z_N{z}_{N-1}\cdots z_{2k+3}{z}_{2k+2}-x_M{x}_M\cdots x_{2k+\text{2}}\cdot v$ 为非负整数，

所以

$\underset{\_}{\underset{\_}{ua}v}=z_{2k+1}{z}_{2k}\cdots z_2{z}_1$ (8)

类似地

$\begin{array}{c}\underset{\_}{va}u=y_{2k+1}{y}_{2k}\cdots y_1\cdot u\\ =y_T{y}_{T-1}\cdots y_{2k+2}{y}_{2k+1}{y}_{2k}\cdots y_1\cdot u-y_T{y}_{T-1}\cdots y_{2k+2}\cdot {10}^{2k+1}\cdot u\\ =vau-y_T{y}_{T-1}\cdots y_{2k+2}\cdot {10}^{2k+1}\cdot u\\ =z_N{z}_{N-1}\cdots z_2{z}_1-y_T{y}_{T-1}\cdots y_{2k+2}\cdot {10}^{2k+1}\cdot u\\ =z_N{z}_{N-1}\cdots z_{2k+3}{z}_{2k+2}\cdot {10}^{2k+1}+z_{2k+1}{z}_{2k}\cdots z_2{z}_1-y_T{y}_{T-1}\cdots y_{2k+2}\cdot {10}^{2k+1}\cdot u\\ =\left(z_N{z}_{N-1}\cdots z_{2k+3}{z}_{2k+2}-y_T{y}_{T-1}\cdots y_{2k+2}\cdot u\right)\cdot {10}^{2k+1}+z_{2k+1}{z}_{2k}\cdots z_2{z}_1\end{array}$

根据引理1得到

$\underset{\_}{\underset{\_}{va}u}=z_{2k+1}{z}_{2k}\cdots z_2{z}_1$ (9)

由式(6)、(8)、(9)得式(5)的结论。证毕。

该引理说明任意三个整数乘积的末连续几位的数字可以由仅仅取中间结果的末连续几位来乘积得到，而根据整数乘法满足交换律，中间结果有两种可能形式，均符合这种性质。我们称这种性质为低位保持原理，很明显多于三个数的乘积也满足这种原理。

引入对n阶非负整数方阵的箝位运算， $\underset{\_}{A}$ 表示A的每个元素钳制到箝位指数控制的范围内，而 $\underset{\_}{AB}$ 表示矩阵A和B先做矩阵乘法再做箝位运算，类似地，可以证明：

$\underset{\_}{AB}=\underset{\_}{A}\underset{\_}{B}$ 且 $\underset{\_}{\underset{\_}{AB}\underset{\_}{C}}=\underset{\_}{ABC}=\underset{\_}{\underset{\_}{A}\underset{\_}{BC}}$ (10)

定理2. 加密解密原理。由从0到 ${10}^{2k+1}-1$ 整数的随机数构成的n阶方阵A，设E为单位矩阵，根据

$\begin{array}{c}\left[A^{2k+1}{10}^{2k+1}+E\right]=\left[{\left(10A\right)}^{2k+1}+E\right]\\ =\left(10A+E\right)\left[{\left(10A\right)}^{2k}-{\left(10A\right)}^{2k-1}+\cdots +{\left(10A\right)}^2-\left(10A\right)+E\right]\\ =\left(10A+E\right)\left\{\left(10A-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10A\right)}^{2i-1}}+E\right\}\end{array}$ (11)

在箝位运算机制下有

$\underset{\_}{\left(10A+E\right)}\underset{\_}{\left\{\left(10A-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10A\right)}^{2i-1}}+E\right\}}=\underset{\_}{\left\{\left(10A-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10A\right)}^{2i-1}}+E\right\}}\underset{\_}{\left(10A+E\right)}=E$ (12)

即 $10A+E$ 与 $\left(10A-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10A\right)}^{2i-1}}+E$ 在箝位运算机制下互逆。

证明：由式(11)和式(10)箝位运算的机制，结论是显然的。证毕。

定理3. 密钥生成。由从0到 ${10}^{2k+1}-1$ 整数的随机数构成的n阶方阵A和B，令

$U=\left(10A+E\right)\left\{\left(10B-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10B\right)}^{2i-1}}+E\right\}$ (13)

及

$V=\left(10B+E\right)\left\{\left(10A-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10A\right)}^{2i-1}}+{\rm E}\right\}$ (14)

则 $\underset{\_}{UV}=\underset{\_}{VU}=E$ ，即U和V在箝位运算下是一对互逆矩阵。

证明：由矩阵乘法和箝位运算的结合律，结论是显然的。

3. 加解密方法

由定理2和3，得到

$\underset{\_}{\left(VU\right)X}=\underset{\_}{V\left(UX\right)}=X$ (15)

利用U、V的互逆性，可以实现加解密。密钥U、V的角色是对称的，如果U作为公钥，那么V作为私钥，或者反之；用作加密与用作数字签名，在计算上没有差异，只是由收、发方加密处理的不同。而且明文(在签名时就是明文的摘要)、密钥和明文均是n阶箝位矩阵，所有元素可以取到0到 ${10}^{2k+1}-1$ 的整数，密钥是随机整数。

又由于密钥

$\begin{array}{c}U=\left(10A+E\right)\left\{\left(10B-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10B\right)}^{2i-1}}+E\right\}\\ =10A\left\{\left(10B-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10B\right)}^{2i-1}}+E\right\}+10\left\{\left(10B-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}\left({10}^{2i-2}{B}^{2i-\text{1}}\right)}\right\}+E\end{array}$ (16)

前两项都含因子10，导致该矩阵除对角线外所有元素末位为0，于是直接用明文矩阵X计算，得到

$UX=10A\left\{\left(10B-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\left(10B\right)}^{2i-2}}+E\right\}X+10\left\{\left(10B-E\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}\left({10}^{2i-2}{B}^{2i-\text{1}}\right)}\right\}X+X$ (17)

则密文矩阵 $\underset{\_}{UX}$ 的所有元素的末尾是X的元素的末位数字。为此，X在加密时先作一种预处理，每个元素的数字右移一位，将个位数设置一个随机数,然后加密，即与密钥作箝位机制下的矩阵乘法。这样处理一举两得，一方面可以避免末位泄露，另一方面自然地引入了随机性，即对相同的明文使用同一密钥生成的密文不同。

由此每个明文单位可对应取到的整数在0到 ${10}^{2k}-1$ 之间。每次进行加密的文本单位的规模是矩阵的阶数平方 $n^2$，这是一种批处理模式，它和RSA、Elgamal等算法的点处理模式明显不同。由于矩阵乘法的复杂度是 $O\left(n^3\right)$ ，平均到每个文本单位的计算复杂度是 $O\left(n\right)$ ，即依密钥尺度呈线性增长，这样的加解密计算的消耗与RSA之类算法相仿。图1给出箝位矩阵加密和签名的算法流程。

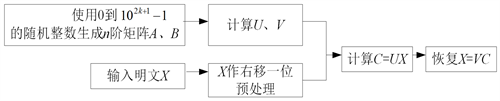
Figure 1. Application of public key cryptography with clamping matrix

图1. 箝位矩阵的公钥密码的运用

4. 密钥安全性分析

破解箝位矩阵的公钥密码，并不意味着直接去计算箝位运算限制下密钥矩阵的逆，因为那意味着关于整数矩阵求解整数形式的箝位逆。更一般的等价形式是求如下的方程

$F\cdot U=G\cdot {10}^{2k+1}+E$ (18)

式(18)中，U是已发布的受攻击的密钥，F就是待定的在箝位运算限制下的U的整数逆。方程右边是一个未定的适配矩阵G，而之所以写成 $G\cdot {10}^{2k+1}+E$ ，是由于右端在箝位限制下变成单位阵的需要。显然，式(18)已经包含了直接求U的箝位逆的情形。事实上，式(18)是一个典型的整系数不定方程如何求取整数解的问题。

首先考虑一个特例，当箝位矩阵的阶数n = 1时，由于方程(18)中U是末位1的整数，与 ${10}^{2k+1}$ 互素，因而可以使用欧几里德辗转相除法，得到确定的整数F、G满足

$F\cdot U=G\cdot {10}^{2k+1}+1$ (19)

辗转相除法的计算复杂度是在 $O\left(\log {10}^{2k+1}\right)=O\left(k\right)$ 级别。但当箝位矩阵的阶数大于1时，对于整数矩阵没有带余除法，且矩阵乘法具不可交换性，因此也没有辗转相除法。式(18)只有从一般的解线性方程组的角度去分析。

一般整系数线性不定方程求取整数解在理论上是可解的 [10] ，通常把一部分变量视作已知量，其余变量写成这些视作已知的变量的表达式。但显然，这样的形式解在这里没有用处，式(18)中必须确定F的具体数字(因而也可确定G的数字)才能破解

$\underset{\_}{F\underset{\_}{UX}}=\underset{\_}{\underset{\_}{FU}X}=X$ (20)

由于式(18)是不定方程，要确定具体的数字解，必须令视作已知的变量取作具体的数字，由于箝位运算导致变量F、G的元素取值在箝位指数控制的范围内(0到 ${10}^{2k}-1$ 之间)，所以尝试取值的可能数目是 ${10}^{2k}$ 。又由于矩阵的元素数目为 $n^2$ ，所以总的取值尝试次数为 ${10}^{2k{n}^2}$ 。当k = 3、n = 10时，这个数目就是10⁶⁰⁰。显然，箝位矩阵公钥的破解难度是依参数k、n呈指数增加的。这里把破解算法归约到枚举该未定矩阵G的所有元素，得出破解强度是NP的结论，就像Elgamal之类的算法是基于离散对数计算归结为枚举所有对数值的困难性一样。

顺便指出，在式(18)中如果直接使用U的常规逆，则F未必为整数矩阵，如此 $F\cdot U$ 的元素的取值必受高于2k + 1位数数字的影响。于是 $F\cdot U$ 虽然为单位阵，但显然 $\underset{\_}{F\cdot \underset{\_}{U\cdot X}}\ne \underset{\_}{\underset{\_}{F\cdot U}\cdot X}=X$ 即不满足结合律式(10)。

综上所述，箝位矩阵公钥系统满足计算复杂性意义下的强度和安全性。

5. 与RSA、Elgamal密码的比较

首先，一个重要的不同是密钥生成的难易程度的差异，RSA需要寻找两个大素数，Elgamal的有限域依赖大素数来构造；其次，RSA的一对公私钥是关于欧拉数模余运算互逆的，当已知一个密钥，求另外一个密钥需要使用辗转相除法来计算。而本文算法在密钥生成时，不需要依赖大素数，只要生成一个指定位长的随机数方阵作为种子，进行若干次矩阵乘法即可获得。最后，RSA、Elgamal对明文加密处理是逐点式的，而本文算法是批处理模式。

RSA密钥长度与选定的大素数数字长短有关，且为增加破解强度而延长密钥长度的代价是搜寻更大的素数；本文算法的密钥长度增长有两个维度，其中以增加矩阵的阶数的方式扩充密钥，增加破解强度，是较容易做到的。在加密解密运算方面，RSA、Elgamal都是运算可交换的，而本文算法基于矩阵乘法，运算有左乘右乘之分。在量子计算里，由于量子的物理性态决定了量子适合对称作用的并发模拟，对非交换的矩阵乘法的并行性模拟反而是其弱项，因此基于矩阵乘法的密码有适应后量子密码时代的特征 [11] [12] [13] [14] [15] 。表1总结了与RSA、Elgamal比较的分析。

Table 1. Comparison with RSA and Elgamal

表1. 与RSA、Elgamal的比较

6. 加解密实验

算法的数据试验采用k = 3、n = 10的参数，即运用箝位指数为7的10阶矩阵作实验，则定理3中的A、B作为种子是10阶7位(十进制位)长随机数构成的矩阵。由于MSVC系统库里的rand()算法的随机数上界的限制，实际使用的是6位长随机数的种子，而生成的其中一个密钥如图2所示。

Figure 2. Key example

图2. 密钥示例

对如图3所示的明文进行加密，加密结果如图4所示。

Figure 3. Plaintext example

图3. 明文示例

Figure 4. Encrypted result

图4. 加密结果

对该密文解密后的结果如图5所示。

Figure 5. Decryption result

图5. 解密结果

为验证末位随机化预处理的效果，考虑上面明文的另一预处理版本(即仅末位不同)，见图6。

Figure 6. Another version of the plaintext example with randomization at the end

图6. 末尾随机化的明文示例的另一版本

使用上面相同的密钥加密后的密文，如图7所示。

Figure 7. Ciphertext encrypted using the key in Figure 2

图7. 使用图2密钥加密后的密文

可见上面两段仅末位不同的明文在相同密钥处理后的密文差异极大，这个反映了箝位密码具有一定的随机性效应。将上面这段密文解密后的明文如下，见图8。

Figure 8. Decryption after encryption of another version of the plaintext example

图8. 明文示例另一版本加密后的解密

使用RSA与本文算法作运算时效对比实验。RSA算法运行不包含大素数选取、密钥生成，只从明文加密再解密恢复的一轮运算时间着手，并且代码经过优化 [16] ；而本文算法包含生成两个随机种子矩阵，再进行密钥生成，然后对明文加密、再解密的一轮运算的时间总和，但代码未经过优化。由于双方对明文处理的长度都不一样，所以本文算法处理时间除以n²，这样可以显示在某个相同基准上衡量两个算法的运算占时(图9的纵轴)。从图9可以看出，对选取的5个算例(图9的横轴)，本文算法比RSA运算占时少了三十多倍。实验结果表明，本文算法在单位明文长度的计算效率上比RSA算法高三十倍。

Figure 9. Comparison of running time between RSA and the algorithm in this paper

图9. RSA和本文算法的运行时效比较

7. 结语

传统的基于有限域或素数的密码系统都有依赖大素数的密钥生成的不易性，本文提出一个密钥生成极其容易的公钥密码系统，且具有因使用矩阵乘法而不易被未来的量子计算产生攻陷危机的优势。由于钳位矩阵与二维码维数匹配的自然特性，下一步拟探索将钳位公钥用于二维码的数字签名的研究。