1. 引言
可控源音频大地电磁法(controlled source audio electromagnetic, CSAMT)是一种重要的地球物理勘探方法,具有抗干扰能力强、分辨力高、勘探深度大等优点,已被广泛应用于矿产资源勘探、油气勘探、地热勘探、地下水文调查等领域 [1] 。CSAMT法沿用了大地电磁法(Magnetotelluric sounding, MT)的观测方式,在远区测量一对正交的水平电磁信号,同时继续使用卡尼亚视电阻率公式。为满足远区测量要求,通常需要在距离发射源数千米到数十千米的区域接收电磁信号,来获得视电阻率和相位信息。但是在实际的野外测量中,由于各方面因素限制,有时不能满足远区测量的要求;其次,远区测量的信号微弱,当存在较强人文干扰时,远区测量的数据信噪比会降低,数据质量得不到保证。
广域电磁法是在CSAMT基础上发展起来的一种人工源频率域电磁测深方法。广域电磁法一方面继承了CSAMT法使用人工源克服场源随机性的优点,采用适合于全域的公式计算广域视电阻率,突破了CSAMT法远区测量的限制,大大拓展了人工源电磁法的观测范围;另一方面,广域电磁法摒弃了CSAMT法变频法的做法,发射源一次发射的是含多个主频成分的伪随机电流信号,而且在测量时只需测量电磁场的一个分量,大大提高了观测速度、野外工作效率 [2] 。何继善等人的研究明确了单分量也具有较好的探测效果。
目前,无论是CSAMT还是广域电磁法,数据解释仍然主要采用一维和二维反演技术。但是随着电磁勘探越来越多地进入复杂地质构造环境中,地下电阻率结构很可能是三维的,一维和二维反演已经很难得到可靠的反演结果,为了充分利用勘探数据信息和提升数据解释精度,发展三维反演技术势在必行。随着计算机技术的飞快进步,三维反演进入实用化已成为可能。反演的基础是正演,正演的计算通常是反演算法里最耗时的部分。前人花费了大量精力开发既能在现有计算机硬件条件下运行,又能准确恢复地下电导率分布的算法 [3] [4] [5] [6] 。
目前广域电磁法的三维正演方面,李帝铨等2013年采用积分方程法实现了广域电磁法三维正演,彭荣华等2018年采用基于二次耦合势的有限体积法实现了广域电磁法三维数值模拟,周印明等2021年基于矢量位和标量位的有限元法实现了广域电磁法三维正演计算,徐锦通等2022年基于谱元法实现了广域电磁法三维数值模拟 [7] [8] [9] [10] [11] 。频率域可控源三维反演方面,目前用的最多的也是最有效的有非线性共轭梯度法(NLCG) [12] - [20] 、有限内存拟牛顿法(LBFGS) [21] [22] [23] [24] [25] 、高斯牛顿法(GN) [26] [27] 等。目前专门针对广域电磁法三维反演还较少有人研究,反演参数如何选择也鲜有报导。
本文开发了基于矢量有限元的三维非线性共轭梯度反演算法,采用的是六面体网格。首先简要介绍了WFEM矢量有限元三维正演算法,然后详细阐述了本文反演算法的细节,包括:目标函数的构建,灵敏度矩阵的计算,正则化策略,反演流程。通过合成算例证明了本文算法的有效性。本文运用Fortran代码,编写了基于矢量有限元的NLCG反演代码,计算使用的处理器型号为AMD Ryzen 5 5600H with Radeon Graphics,主频为3.30 GHz,16G个人PC机。
2. 三维正演计算
从微分形式的麦克斯韦方程组出发,取时谐因子为
,可得电性源广域电磁法满足的麦克斯韦方程组
(1)
(2)
上式中:
为电场强度,单位为V/m;
为磁场强度,单位为A/m;
,
为角频率(rad/s),
为磁导率(H/m),
为电导率(S/m),
为介电常数(F/m),
为外界激发的电性源的电流密度(A/m2),电流强度为I,长度为dl的电偶极子源的电流密度为
(3)
其中
为场源所在位置,
为空间任一点所在位置,
为狄拉克函数,其表达式为
(4)
因此电流密度在非场源点处为0,而在源点处可以取
,为麦克斯韦方程组的“奇异点”。为了避免源点处的奇异性,通常有两种策略,本文使用总场算法,采用伪
函数,将源点分布到一个小的区域,消除源点奇异性。忽略位移电流,消去磁场,推导了总场满足的电场双旋度控制方程
(5)
其中,k为准静态条件下的波数,
。
为了保证电场的唯一性,本文使用迪利克雷边界条件,在正演时对计算区域进行扩边处理。利用矢量有限元法对上式进行离散化得到待求解的线性方程组
(6)
其中,系数矩阵
为大型稀疏复对称矩阵,
为待求解的整个计算域的网格单元棱边上的电场值列向量,
为右端源向量。本文使用直接解法,通过调用直接求解器Pardiso对上式进行高精度求解。
3. 三维反演理论
3.1. 目标函数的构建
本文中,广域电磁法三维反演目标函数采用Tikhonov正则化 [28] 方式来构建,目标函数可定义为,即:
(7)
上式中,
为数据拟合差函数,
为模型正则化函数,
为正则化因子,为保证求取的电阻率有意义,减少虚假异常,对反演过程中的电阻率添加了上下限约束 [29] ,反演过程中的模型参数
设为:
(8)
上式中
和
分别为第k个六面体单元的转换域模型参数和真实模型参数,b和a分别表示模型的上限和下限。
数据拟合差函数可表示为:
(9)
其中,
为观测数据,本文的观测数据采用的是
的振幅,
为正演预测数据,
为数据加权矩阵,可表示为
(10)
其中
为第j个数据的误差,模型正则化函数为
(11)
上式中
为包含地球物理先验信息的参考模型,
为模型粗糙度矩阵。本文采用最平滑模型约束,
由三维拉普拉斯矩阵的近似得到,常表示为以下形式 [30] :
(12)
其中
,
和
分别为离散拉普拉斯矩阵x,y和z方向的平滑参数,
、
、
分别为x,y和z方向上的二阶差分矩阵。目标函数确立后,反演问题就转为极小化目标函数的问题。
3.2. 梯度的计算
因为本文主要采用的是
的振幅(实数)反演,若是观测数据使用的是复数,则目标函数及相应的梯度皆要有所改变,对目标函数求梯度得
(13)
上式中
为灵敏度矩阵,也称为雅可比矩阵,是由模型响应函数对模型参数的一阶微分构成。具体的公式推导在附录中给出。本文的正则化参数采用冷却法更新正则化参数,即
(14)
上式中,k一般取为0.1,正则化参数在反演的初始阶段选取较大的参数来保证反演的稳定性,随着反演的进行,逐渐减小正则化参数来降低模型正则化项的权重,使得反演集中在数据的拟合上,直到达到最佳的数据拟合差。
3.3. 反演流程
广域电磁法三维非线性共轭梯度反演算法的大致流程为
1) 设置迭代次数k = 0,读取反演的初始模型、观测数据、网格参数、反演控制参数等;
2) 三维正演,计算正演预测数据
、当前模型参数下的目标函数
、均方根误差rms;若rms达到设定的精度,则退出循环,结束程序,否则继续;
3) 伴随正演,计算当前模型参数下的目标函数梯度
;
4) 计算搜索方向
,第一次迭代的搜索方向为负梯度方向;
5) 线搜索相对最佳步长
,使得
满足Armijo条件则退出线搜索;
6) 更新模型参数
,更新负梯度向量
;
7) 更新预条件矩阵
、参数
;
8) k = k + 1,回到步骤(2)。
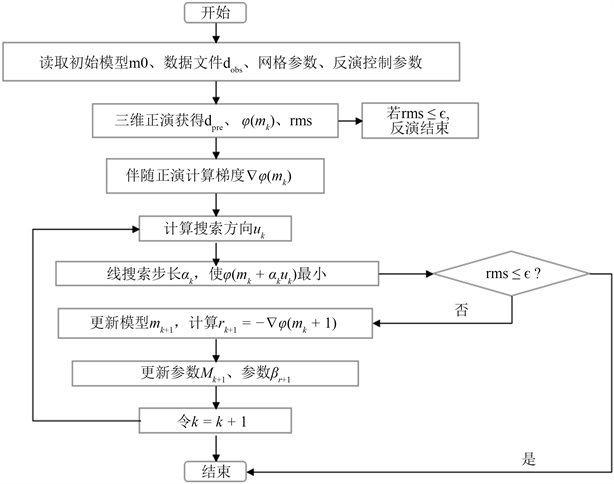
Figure 1. Three-dimensional NLCG inversion flowchart
图1. 三维NLCG反演流程图
由上图1可知,三维非线性共轭梯度反演算法主要的计算量在于梯度的计算和步长的搜索。NLCG算法对于初始模型的依赖程度较高,一个好的初始模型能让反演更快地收敛。同时预条件算子起到了加速反演的作用。
4. 理论模型合成数据反演算例
模型一:设计了如图2所示的低阻异常体模型,低阻异常体大小为1000 m*1000 m*500 m,它的中心坐标为(0, 5000, 750) m。低阻体的电阻率为10 Ωm,位于电阻率为100 Ωm的均匀半空间中。线源沿着x方向布置,长度为100 m,电流大小为1 A,线源的中心坐标为(0, 0, 0) m,选取8 Hz~512 Hz呈对数分布的七个频点的数据。布设了21 × 21个测点,点距100 m,线距也是100 m,均匀的分布在地表,测区范围为
,
。正演网格剖分为58 × 64 × 50个六面体单元,反演网格剖分为30 × 45 × 22个六面体单元。所输入的观测数据为Ex的振幅,总共获得了3087个添加了3%高斯噪声的合成数据。反演区域为:
,
,
。
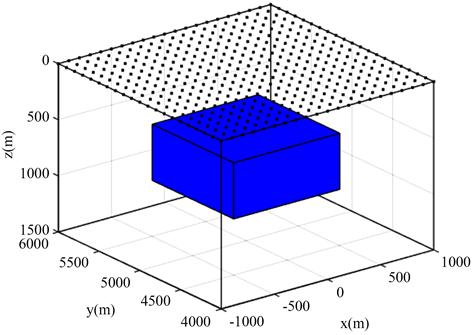
Figure 2. Schematic diagram of the low-resistance body model
图2. 低阻体模型示意图

Figure 3. Profile view of the 3D inversion results of the low-resistance body model
图3. 低阻体模型三维反演结果剖面图
反演的目标拟合差设为1.02,反演初始正则化参数设为100,反演的初始模型和参考模型均设为100 Ωm的均匀半空间,反演迭代16次收敛到目标拟合差。上图3给出了三维反演所得到的最后地电模型结果,对比各切片图可知,低阻异常体的位置比较好的被刻画出来,低阻异常体的电阻率值恢复到40左右,但是由y方向切片可知,在低阻异常体边缘位置,出现了明显高阻假异常。可能的原因是只使用Ex反演,缺少y方向数据信息,导致在y方向信息不足,反演多解性增强。
为了比较反演得到的最终模型和真实模型之间的差异,将频率为8 Hz时模型一的合成数据及反演得到的最终模型的正演数据做比较,可得下图4,图4中黑色的小点代表测点,结果显示预测数据很好的拟合了合成数据,合成数据不光滑的原因是因为被加了3%的高斯噪声。同时反演的rms收敛曲线如下。
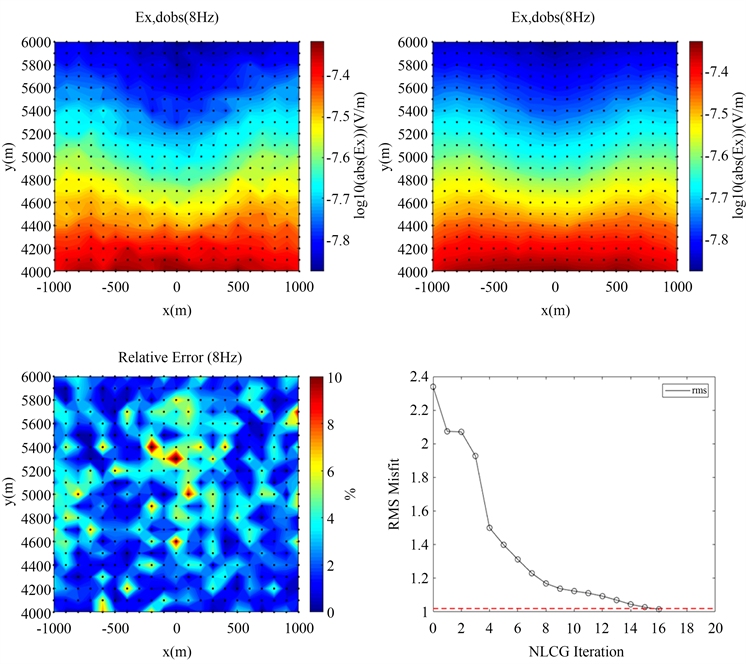
Figure 4. Model 1 forward response comparison chart and inversion fitting difference convergence curve
图4. 模型一正演响应对比图及反演拟合差收敛曲线图
为了探究广域电磁法的可测量区域,对比了不同收发距情况下的反演效果。在模型一的基础上设计了异常体中心与源的收发距与异常体底部埋深之比为3倍、5倍及7倍的不同模型,即收发距3000 m、5000 m、7000 m,其他条件不变,反演结果如下(见图5)。
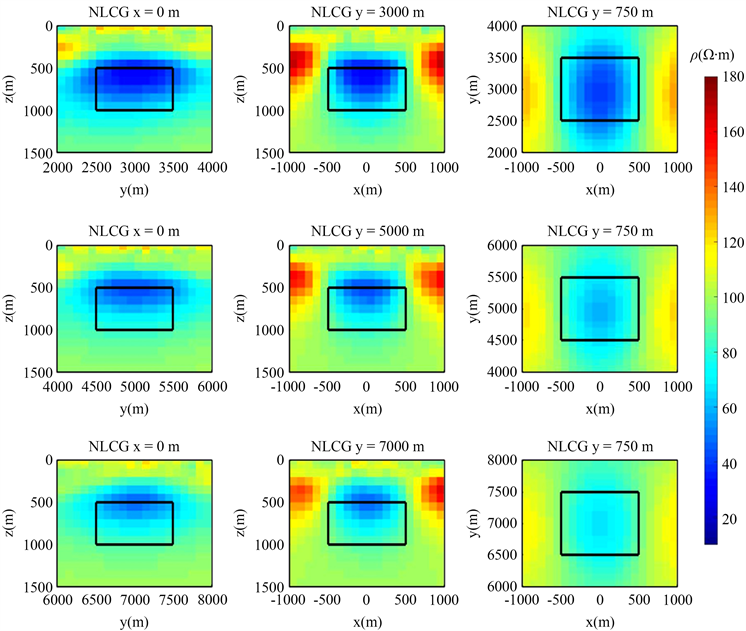
Figure 5. Profile view of 3D inversion results of low-resistance body models with different transmit and reception distances (First line, sending and receiving distance 3000 m; the second line, the sending and receiving distance is 5000 m; Third line, sending and receiving distance 7000 m)
图5. 不同收发距低阻体模型三维反演结果剖面图(第一行,收发距3000 m;第二行,收发距5000 m;第三行,收发距7000 m)
由图5可以看出,不同收发距的反演都把异常体的位置比较好的被刻画出来,结果表明,广域单分量测深效果在较大的收发距范围内都有效果,证实了即使在不满足远区条件下,广域电磁法仍能取得较好的探测效果,验证了广域电磁法三维反演的优势。
模型二:为了进一步测试反演算法的准确性,设计了如图6所示的棋盘模型,异常体大小均为400 m*400 m*400 m,异常体中心埋深均为400 m。低阻体的电阻率为10 Ωm,高阻体的电阻率为1000 Ωm,位于电阻率为100 Ωm的均匀半空间中。线源沿着x方向布置,长度为100 m,电流大小为1 A,线源的中心坐标为(0, 0, 0) m,选取8 Hz~512 Hz七个呈对数分布频点的数据。布设了21 × 21个测点,点距100 m,线距也是100 m,均匀的分布在地表,测区范围为
,
。正演网格剖分为63 × 64 × 51个六面体单元,反演网格剖分为30 × 45 × 22个六面体单元。所输入的观测数据为Ex的振幅,总共获得了3087个添加了3%高斯噪声的合成数据。反演区域设为:
,
,
。
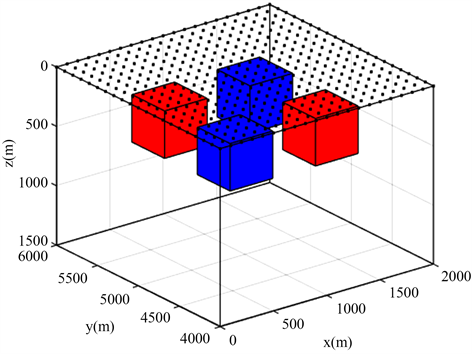
Figure 6. Schematic diagram of the checkerboard model
图6. 棋盘模型示意图
反演结果如下图7所示,由图7可知,不同剖面的反演结果都比较好地刻画出高低阻异常体的位置,对于异常体电阻率的恢复,低阻异常体的电阻率最小值约为40 Ωm,高阻异常体的电阻率最大值约为200 Ωm。可以看出低阻异常体的恢复更接近真实模型。这反映了电磁法对低阻体和高阻体不同的分辨率。

Figure 7. Schematic diagram of the checkerboard model plan
图7. 棋盘模型平面示意图
反演结果如下图8所示。

Figure 8. A profile view of the checkerboard model inversion result
图8. 棋盘模型反演结果剖面图
反演的rms收敛曲线如下,为了揭示合成数据和预测数据的差异,反演合成数据与初始模型响应数据和反演最终模型响应数据振幅比率统计图如下,如果振幅比是接近1,则观测数据和预测数据的差距接近为0。由图9可知,我们在给合成数据加了5%高斯噪声的基础上,获得了不错的拟合差。
将反演的观测数据从Ex振幅换成复数,重新反演模型四,反演结果如下(见图10),可以看出反演Ex与只反演Ex振幅相比,二者的反演结果非常相似。但是在细节上,反演Ex的结果要优于只反演振幅的结果,得到的高阻体电阻率最大值约为250 Ωm,低阻体电阻率最小值约为18 Ωm,对异常体电阻率的恢复要优于只反演振幅的结果。

Figure 9. Checkerboard model fitting difference convergence curve
图9. 棋盘模型拟合差收敛曲线图
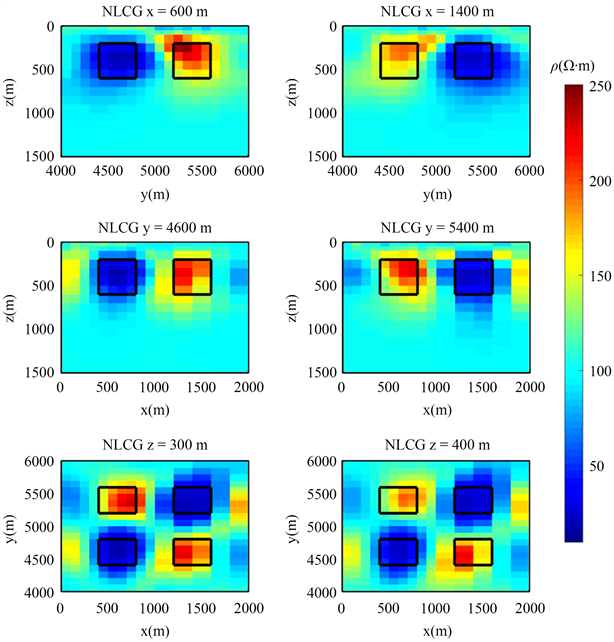
Figure 10. A profile view of the checkerboard model inversion result (Complex Inversion)
图10. 棋盘模型反演结果剖面图(复数反演)
反演的rms收敛曲线如下图11所示。

Figure 11. Checkerboard model fitting difference convergence curve (Complex Inversion)
图11. 棋盘模型拟合差收敛曲线图(复数反演)
5. 结论
本文实现了一种广域电磁法三维反演算法,正演采用矢量有限元法对控制方程进行离散化,通过直接解法求解大型稀疏线性方程组,该方法在三维电磁法中精度较高,反演采用非线性共轭梯度法(NLCG),它具有较高的稳定性,在三维反演中比较成熟,不需要显式计算和存储灵敏度矩阵。以上技术的结合使用使得本文的反演算法具有较高的准确度和稳定性。
通过几个模型算例可以看出开发的反演算法能够很好地反映异常体的位置和形态,比较了不同收发距的反演效果,验证了广域电磁法三维反演的优势,证实了单分量也能具有很好的探测效果。但是由于只使用Ex反演,缺少了y方向的信息,导致在y方向异常体的边界附近容易出现伴生的假异常。
最后我们还比较了用Ex振幅和使用Ex复分量反演的效果,证实使用Ex复分量反演比只用Ex振幅反演细节还原的更好,更能恢复异常体的电阻率。为了进一步测试本文算法的可靠性,下一步将开展实测数据反演,以便对本文开发的算法进行完善。
附录:灵敏度矩阵的计算
非线性共轭梯度算法不直接计算和存储灵敏度矩阵
,而是采用伴随正演的方式求取灵敏度矩阵和向量的乘积。
灵敏度矩阵可表示为
(A1)
其中矩阵
可表示为
(A2)
上式中
是插值算子,因此灵敏度矩阵及其转置与向量的乘积为
(A3)
令
,则可通过求解伴随正演求出
,
(A4)
计算
实际上就是利用新的右端项进行一次正演,得到
后即可获得灵敏度矩阵转置与向量的乘积
(A5)