单平面有向无圈图中最小路覆盖问题的算法研究

Research of Minimum Path Covering Problem Algorithm in Single Planar Directed Acyclic Graph

摘要: 一个铁路区段在规划时间内的时空网络是一个仅包含一对源与汇的有向无圈平面图。每个列车都可由该网络中的一条有向路表示。本文研究上述网络中的最小路覆盖问题，即至少用多少条有向路可以覆盖图中所有的边。根据单平面有向无圈图的单源单汇和平面性等结构性质，本文给出了上述问题的一个时间复杂度为O(nk)的精确算法，这里n表示图中顶点数、k表示图中最大有向割所包含边的数目。

Abstract: The space-time network of a railway section in the planning time is a directed acyclic graph that contains only a pair of sources and sinks. Each train can be represented by a directed path in the network. In this paper, we study the minimum path covering problem in the above network, that is, at least how many directed paths can cover all edges in the network. According to the structural properties of single-source, single-sink and planarity, we give an O(nk) time exact algorithm to solve the minimum path covering problem in single planar directed acyclic graph, where n is the number of vertices in graph and k is the number of edges in the maximum directed cut.

1. 引言

在货运铁路运输当中，商品在铁路运输中是由火车运输的。火车由机车和火车车厢组成。火车车厢用来装载货物，机车为火车的运行提供动力。在规划时间内，一段铁路区间上表示货运需求的时空网络是一个仅包含一对源与汇的平面有向无圈图，从而列车的行驶路线可由该网络中的一条有向路表示。

在研究铁路上的货运分配问题，常用的策略是确定铁路通道的一个主要方向，重点是研究沿这个方向的货物流动。比如，Caprara [1] 考虑的是铁路中的南北方向。因此，我们可将所有的货运走廊分配一个特定的方向，而不考虑任何沿相反方向移动的路径，故可用一个平面有向无圈图代表铁路通道，其弧形集表示铁路线段的集合，节点集表示线段之间的货运站点的集合。

本文考虑可带重边的有向无圈图。首先给出一些基本的定义和符号。 $D=\left(V,A\right)$ 是有向图，V表示图中顶点组成的集合，A表示图中有向边组成的集合。对D的任意边 $a=\left(u,v\right)$ ，u为a的尾部，v为a的头部。对D的任意顶点v， ${\delta }^{+}\left(v\right)$ 表示以v为尾部的边组成的集合， ${\delta }^{-}\left(v\right)$ 表示以v为头部的边组成的集合。p是D中的一条带定向的路(圈)，如果其定向与D相同，则称p是D中的一条有向路(圈)。若有向图D不包含任意有向圈称其为有向无圈图。若图D可画到平面上使得它的边仅在端点相交则称其为平面图。其它术语可参考文献 [2] 。

有向无圈图的最小路覆盖问题是找覆盖有向无圈图所有边的有向路集合使得路的数目最少。一种方法是转化为最大匹配问题。第一步是计算有向无圈图D的边传递闭包 $TC\left(D\right)$ ，然后将D的最小路覆盖问题转化为 $TC\left(D\right)$ 的最小路因子问题。Ntafos和Hakimi [3] 将最小路因子问题转换为最大二分匹配问题，而解决最大二分匹配的最好算法其时间复杂度为 ${\rm O}\left(n^{2.5}\right)$ [4] 和 ${\rm O}\left(\sqrt{n}m\right)$ [5] ，这里n为图中顶点数目、m为图中边的数目。另一种方法是将最小路问题转化为具有单位下界的最小可行流问题，即首先找到最小流，然后通过分解算法将流分解为有向路。Ahuja [6] 通过两次应用任何寻找最大流的算法找到最小可行流。最著名的最大流量算法由Goldberg [7] 和Orli [8] 给出，从而最小可行流问题在 ${\rm O}\left({\left|V\right|}^2{\left|A\right|}^{0.5}\right)$ 时间和 ${\rm O}\left(\left|V\right|\left|A\right|\right)$ 时间解决，其中 $\left|V\right|$ 是网络的顶点数、 $\left|A\right|$ 是网络的边数。虽然有向无圈图的流分解可以在线性参数时间内计算，但是解决问题的时间复杂度至少是参数的二次方数量级。

本文主要研究单平面有向无圈图的最小路覆盖问题，并针对问题设计了一个时间复杂度为 ${\rm O}\left(nk\right)$ 的精确算法，这里n为图的顶点数目、k为图的最大有向割中边的数目。

2. 相关定义

首先给出算法设计和分析过程中需要用到的一些定义。

定义(平面有向无圈图)设D是一个有向无圈图，如果D是一个平面图，则称D是一个平面有向无圈图。

定义(最小路覆盖问题)设D是一个有向无圈图，最小路覆盖问题是找到D的一个有向路集合 $\left\{p_1,\cdots ,p_i\right\}$ 其满足i最小且 $A\left(D\right)={\displaystyle {\cup }_{1\le j\le i}A\left(p_j\right)}$ 。覆盖D的最小路径数记为 $pc\left(D\right)$ 。

定义(可比关系)设D是一个有向无圈图，如果存在一条有向路连接 $a^{\prime }=\left(u^{\prime },v^{\prime }\right)$ 到 $a^{″}=\left(u^{″},v^{″}\right)$ ，则称 $a^{\prime }$ 可比于 $a^{″}$ ，记作 $a^{\prime }\prec a^{″}$ 。如果不存在一条有向路连接 $a^{\prime }=\left(u^{\prime },v^{\prime }\right)$ 到 $a^{″}=\left(u^{″},v^{″}\right)$ ，则记作 $a^{\prime }\nprec a^{″}$ 。如果 $a^{\prime }$ 与 $a^{″}$ 满足 $a^{\prime }\nprec a^{″}$ 且 $a^{″}\nprec a^{\prime }$ ，则称 $a^{\prime }$ 与 $a^{″}$ 不可比，记作 $a^{\prime }\times a^{″}$ 。

定义(源s与汇t)设D是一个有向无圈图，如果 ${\delta }^{-}\left(s\right)=\varnothing$ ，则称顶点s是源。如果 ${\delta }^{+}\left(t\right)=\varnothing$ ，则称顶点t是汇。

定义(面)设D是一个有向无圈图，如果平面被D分成有限数量的连通区域并且F是这些区域之一，则称F是一个面。如果面F是无界的，则称F为外表面。

定义(单平面有向无圈图)设 $D=\left(V\cup \left\{s,t\right\},A\right)$ 是一个平面有向无圈图，如果其只有一个源s和一个汇t且都位于外表面的边界，则称 $D=\left(V\cup \left\{s,t\right\},A\right)$ 是一个单平面有向无圈图。

图1展示了一个单平面有向无圈图的例子。

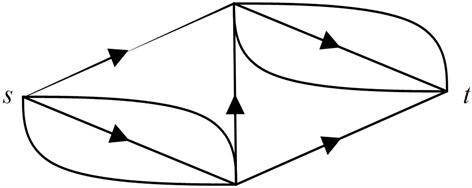
Figure 1. A single planar directed acyclic graph

图1. 一个单平面有向无圈图

定义(有向割)设D是一个有向无圈图，如果 $S\subset V$ 且 ${\delta }^{-}\left(S\right)=\varnothing$ ，则称 ${\delta }^{+}\left(S\right)$ 是D的一个有向割。此外，D的最大有向割中边的数目记作 $\left|{\delta }^{+}\left(D\right)\right|$ 。

例如图1中 ${\delta }^{+}\left(s\right)$ 是该图的一个有向割，其也是一个最大有向割。

定义(界边boundary arc)设D是一个单平面有向无圈图，如果边a是外表面的边界，则称a是一条界边。

定义(界路boundary path)设 $D=\left(V\cup \left\{s,t\right\},A\right)$ 是一个单平面有向无圈图，如果p是一条连接s与t的路且其每条边都是界边，则称p是一条界路。

定义(反链)设D是一个有向图， $A_0$ 是D中的一个非空边集合。如果边集 $A_0$ 中任意两个互异的边都不可比，则称边集 $A_0$ 是D的一个反链。

3. 算法设计与分析

本文给出了时间复杂度为 ${\rm O}\left(nk\right)$ 精确算法来解决单平面有向无圈图中的最小路覆盖问题，这里n表示图中顶点数目、k表示最大有向割中边的数目。算法是根据图的单源单汇性，平面性和有向无圈性进行设计的。本文中算法的设计思路是先找单平面有向无圈的一条界路，然后按照找到的界路进行删边，最后恢复最少的边以保持图中其余边的可变关系不发生改变。

算法1是最小路覆盖算法，该算法为主算法。首先调用算法1，对每个顶点v建立一个新的标签并附为空。其次判断图中是否存在边未被有向路所覆盖。如果存在未覆盖的边，则需要找一条新的有向路，从而进入算法2找新的界路。如果不存在未覆盖的边，则算法停止，输出所找到的有向路集合。算法1的伪代码如下。

Algorithm 1. Minimum path cover algorithm

算法1. 最小路覆盖算法

寻路算法是算法1调用的子算法，其利用单平面有向无圈的结构特点，找出一条界路并依次处理路中的边。首先从源点s出发，找一条界边，并将界边的头端点与尾端点关联。其次判断是否存在新的界边与前一个界边相关联。如果存在，则继续调用算法2，然后寻路。否则调用算法3，对有向路中的边做处理。下面给出算法步骤：

Algorithm 2. Path-finding algorithm- $Pf\left(D,v\right)$

算法2. 寻路算法– $Pf\left(D,v\right)$

删除算法是算法2调用的子算法，其作用是处理已找到有向路中的边。首先判断是否存在未处理的界边。如果不存在，则有向路中所有的界边都被处理，算法停止。如果存在，则找出相应的界边并将其从图中删除。然后判断被删除的界边是否影响其他边的可比关系，若不影响则继续调用算法3，否则调用算法4。删除算法的伪代码如下。

Algorithm 3. Deletion algorithm- $Delete\left(D,u\right)$

算法3. 删除算法– $Delete\left(D,u\right)$

恢复算法是算法3调用的子算法，其作用是恢复最少的界边以保持其它边的可比关系不变。首先判断顶点是否为源点。如果顶点为源点，则恢复界边数为0，算法停止。如果非源点，则进行判断所恢复的界边集是否能保持可比关系不变。若能保持，则将界边集合添加到图中，然后调用算法3。若不能，则继续调用算法4来寻找满足条件的界边集。算法的伪代码如下。

定理1 设 $D=\left(V\cup \left\{s,t\right\},A\right)$ 是一个单平面有向无圈图，算法1可在 ${\rm O}\left(n\left|{\delta }^{+}\left(D\right)\right|\right)$ 时间内找到覆盖D的最小有向路集合 $\left\{p_1,\cdots ,p_i\right\}$ ，这里n为图中顶点数目、 $i=\left|{\delta }^{+}\left(D\right)\right|$ 。

为方便证明定理1，我们先给出一些命题及其证明。

命题2 如果 $D=\left(V,A\right)$ 是一个有向无圈图，则 $pc\left(D\right)\ge \left|{\delta }^{+}\left(D\right)\right|$ 。

Algorithm 4. Recovery algorithm- $Recover\left(D,v\right)$

算法4. 恢复算法– $Recover\left(D,v\right)$

证明对于有向无圈图 $D=\left(V,A\right)$ 中任意有向割 ${\delta }^{+}\left(S\right)$ ，其满足 ${\delta }^{-}\left(S\right)=\varnothing$ ，故D中任意有向路p至多包含 ${\delta }^{+}\left(S\right)$ 中一条边。由于 $pc\left(D\right)$ 是最小有向路覆盖数，所以 $pc\left(D\right)\ge \left|{\delta }^{+}\left(D\right)\right|$ 成立。

事实上，当D是有向无圈图时，其满足 $pc\left(D\right)=\left|{\delta }^{+}\left(D\right)\right|$ ，这一结论可直接由定理的证明得出。

命题3 设 ${\delta }^{+}\left(S\right)$ 是单平面有向无圈图 $D=\left(V\cup \left\{s,t\right\},A\right)$ 的一个最大有向割，如果p是一条界路，那么 $\left|{\delta }^{+}\left(S\right)\cap A\left(p\right)\right|=1$ 成立。

证明令 ${\delta }^{+}\left(S\right)$ 是单平面有向无圈图 $D=\left(V\cup \left\{s,t\right\},A\right)$ 的一个最大有向割。因为 ${\delta }^{-}\left(S\right)=\varnothing$ 且D有唯一源s汇t，所以 $s\in S$ 且 $t\notin S$ 。由于p是连接s和t的界路并且 ${\delta }^{+}\left(S\right)$ 将s与t分割开，故有向路p与 ${\delta }^{+}\left(S\right)$ 由交集，即 $\left|{\delta }^{+}\left(S\right)\cap A\left(p\right)\right|\ge 1$ 。又因为 ${\delta }^{-}\left(S\right)=\varnothing$ ，所以 $\left|{\delta }^{+}\left(S\right)\cap A\left(p\right)\right|\le 1$ 。综上， $\left|{\delta }^{+}\left(S\right)\cap A\left(p\right)\right|=1$ 成立。

命题4 如果D是一个有向无圈图，那么其最大有向割中边的数目等于最大反链中边的数目。

证明设 ${\delta }^{+}\left(S\right)$ 是D的一个最大有向割。由于 ${\delta }^{-}\left(S\right)=\varnothing$ ，故 ${\delta }^{+}\left(S\right)$ 中任意两条边不能在同一条有向路中，所以 ${\delta }^{+}\left(S\right)$ 是D的一个反链。另一方面，设 $A^{\prime }$ 是D的一个最大反链，我们构造边集合 $A^{″}=\left\{a\in A-A^{\prime }:\exists a^{\prime }\in A^{\prime },a\prec a^{\prime }\right\}$ 且将 $A^{″}$ 中所有边的顶点记作 $V^{″}$ 。根据 $A^{″}$ 的构造可得 ${\delta }^{-}\left(V^{″}\right)=\varnothing$ ，从而 ${\delta }^{+}\left(V^{″}\right)$ 是一个包含 $A^{\prime }$ 的有向割。综上，有向无圈图的最大有向割中边的数目等于其最大反链中边的数目。

命题5 设 $D=\left(V\cup \left\{s,t\right\},A\right)$ 是一个单平面有向无圈图，如果 $D^{\prime }$ 是由D经过 $Recover\left(D,v\right)$ 阶段得到，那么 $D^{\prime }$ 中边的可比关系与D中相同。

证明在算法的 $Recover\left(D,v\right)$ 阶段，首先判断该顶点是否为源点s。如果是s则算法停止，否则对该点的出度 $\left|{\delta }^{+}\left(v\right)\right|$ 进行判断。一方面，如果 $\left|{\delta }^{+}\left(v\right)\right|>0$ 则 $B_i$ 是连接两条可比界边的有向路的边集，并且这条有向路中非端点的度都为2，因此删除 $B_i$ 不改变其他边的可比关系。另一方面，如果 $\left|{\delta }^{+}\left(v\right)\right|=0$ 则分情况考虑v入度的情况。如果 $\left|{\delta }^{-}\left(v\right)\right|\ge 2$ ，则v变为一个断点(入度非零，出度为零)。对于这种情况，我们需要将 $B_i$ 中的边恢复到图中去，才能保证图中边的可比关系不变。如果 $\left|{\delta }^{-}\left(v\right)\right|=1$ ，则在图中删除相应的界边 $\left(u,v\right)$ ，使v变为一个孤立点。因为不确定删除 $\left(u,v\right)$ 是否会影响其余边的可比关系，所以将其暂存到 $B_i$ 中，然后继续执行 $Recover\left(D,u\right)$ 。综上，命题得证。

命题6 设 $D=\left(V\cup \left\{s,t\right\},A\right)$ 是一个单平面有向无圈图，如果 $D^{\prime }$ 是由D经过 $Delete\left(D,v\right)$ 阶段得到，那么 $D^{\prime }$ 中边的可比关系与D中相同。

证明在算法的 $Delete\left(D,v\right)$ 阶段，首先判断是否存在未处理的的界边 $\left(u,v\right)$ 。如果存在则对v的入度进行讨论，否则本阶段结束。对于 $\left|{\delta }^{-}\left(v\right)\right|=0$ 的情况：如果 $\left|{\delta }^{+}\left(v\right)\right|>0$ ，则恢复边 $\left(u,v\right)$ ，从而其他边的可变关系不变；如果 $|{\delta }^{+}(v)|$ $=0$，则v变为孤立点，然后暂存边 $\left(u,v\right)$ 到 $B_i$ 并执行 $Recover\left(D,u\right)$ ，由命题5知，其余边的可变关系不变。对于 $\left|{\delta }^{-}\left(v\right)\right|>0$ 的情况，如果 $\left|{\delta }^{+}\left(u\right)\right|>0$ 则执行 $Delete\left(D,u\right)$ ，否则对u的入度进行讨论。如果 $\left|{\delta }^{-}\left(u\right)\right|=0$ ，则u为源点，算法停止。如果 $\left|{\delta }^{-}\left(u\right)\right|=1$ ，则找一条界边 $\left(w,u\right)$ 并执行 $A-\left\{\left(w,u\right)\right\}$ 使得u为孤立点，然后执行 $Recover\left(D,u\right)$ ，由命题5知，其余边的可变关系不变。如果 $\left|{\delta }^{-}\left(u\right)\right|>1$ ，则u为一个断点，故需要恢复 $\left(u,v\right)$ ，然后执行 $Delete\left(D,u\right)$ 。

下面为不恢复某些边却能保证其余边的可比关系不变的原因。如果 $\left(u,v\right)$ 是 $D=\left(V\cup \left\{s,t\right\},A\right)$ 中的一条界边且满足 $\left|{\delta }^{+}\left(u\right)\right|\ge 2$ 且 $\left|{\delta }^{-}\left(v\right)\right|\ge 2$ ，那么 $D^{\prime }=\left(V\cup \left\{s,t\right\},A-\left\{\left(u,v\right)\right\}\right)$ 满足 $\left|{\delta }^{+}\left(u\right)\right|\ge 1$ 且 $\left|{\delta }^{-}\left(v\right)\right|\ge 1$ 。由于 $D^{\prime }=\left(V\cup \left\{s,t\right\},A-\left\{\left(u,v\right)\right\}\right)$ 仍是单平面有向无圈图，故存在s-v有向路和u-t有向路。因为 $D^{\prime }$ 是一个平面图其边只在顶点处相交，所以上述两条路必在某顶点处相交，即 $D^{\prime }$ 中存在连接uv的有向路，从而以u为头部的边和以v为尾部的边间的可比关系不变。

定理1 的证明。根据算法1，记 $D=D_0,D_1,\cdots ,D_i$ 为每次while产生的单平面有向无圈图，记 $p_j$ 为在 $D_{j-1}$ 中Visit阶段找到的界路。要证明 $i=\left|{\delta }^{+}\left(D\right)\right|$ 成立，只需证明 $\left|{\delta }^{+}\left(D_j\right)\right|=\left|{\delta }^{+}\left(D_{j+1}\right)\right|+1$ 对任意的 $0\le j\le i-1$ 成立。

首先证明 $\left|{\delta }^{+}\left(D_{j+1}\right)\right|<\left|{\delta }^{+}\left(D_j\right)\right|$ 。假设 $\left|{\delta }^{+}\left(D_{j+1}\right)\right|\ge \left|{\delta }^{+}\left(D_j\right)\right|$ 成立，则 $D_{j+1}$ 中存在 $\left|{\delta }^{+}\left(D_{j+1}\right)\right|$ 条互不可比的边，不妨记为 ${\delta }^{+}\left(D_{j+1}\right)$ 。由命题6知 ${\delta }^{+}\left(D_{j+1}\right)$ 在 $D_j$ 中是互不可比的。根据命题4得到 $D_j$ 的最大有向割中边的数目不小 $\left|{\delta }^{+}\left(D_{j+1}\right)\right|$ ，从而 $\left|{\delta }^{+}\left(D_j\right)\right|\ge \left|{\delta }^{+}\left(D_{j+1}\right)\right|>\left|{\delta }^{+}\left(D_j\right)\right|$ 成立，矛盾。然后证明 $\left|{\delta }^{+}\left(D_{j+1}\right)\right|\ge \left|{\delta }^{+}\left(D_j\right)\right|-1$ 。根据命题3，如果 ${\delta }^{+}\left(S\right)$ 是 $D_j$ 中任意最大有向割，则 $\left|A\left(p_{j+1}\right)\cap {\delta }^{+}\left(S\right)\right|=1$ 。由命题6知 ${\delta }^{+}\left(S\right)-A\left(p_{j+1}\right)$ 是 $D_{j+1}$ 中的反链，故 $\left|{\delta }^{+}\left(D_{j+1}\right)\right|\ge \left|{\delta }^{+}\left(D_j\right)\right|-1$ 成立。综上，当 $0\le j\le i-1$ 时， $\left|{\delta }^{+}\left(D_j\right)\right|=\left|{\delta }^{+}\left(D_{j+1}\right)\right|+1$ 成立。

由命题2知 $pc\left(D\right)\ge \left|{\delta }^{+}\left(D\right)\right|$ ，所以算法1输出的有向路集合 $\left\{p_1,\cdots ,p_i\right\}$ 是最优解，这里 $i=\left|{\delta }^{+}\left(D\right)\right|$ 。

算法的时间复杂度是 ${\rm O}\left(n\left|{\delta }^{+}\left(D\right)\right|\right)$ 。步骤1中for循环是对图中每个顶点做一次操作，总共是n次。while阶段每次先找一条边界路，然后沿着这条路依次对边做操作，路上每条边至多被删、暂存，恢复各1次，所以每阶段操作 ${\rm O}\left(n\right)$ 次。由上面分析知，while阶段会找到 $\left|{\delta }^{+}\left(D\right)\right|$ 条路，所以while循环中所要操作的次数为 ${\rm O}\left(n\left|{\delta }^{+}\left(D\right)\right|\right)$ 。综上，该算法的时间复杂度为 ${\rm O}\left(n\left|{\delta }^{+}\left(D\right)\right|\right)$ 。

为让读者更好的理解算法，我们在图2展现出算法在图1中的运行过程。首先，判断图中存在未被覆盖的边，则找到一条界路Path1，图中用红色虚线表示Path1，删除路中的边后，其他边的可比关系不变，无需恢复边。其次，判断图中存在未被覆盖的边，则找到一条界路Path2，但删除路中的边后边间的可比关系发生改变，故需恢复第二条边来保持边的可比关系。再次，判断图中存在未被覆盖的边，则找到一条界路Path3，发现删除路中头部两条边后可能影响边的可比关系，故对此段删除的边暂存，经过我们判断暂存边集不影响剩余边的可比关系，故将暂存边集删除。最后，图只剩一条路，此为界路Path4，算法结束。为了更加直观展现图2中所找的路，我们将路集合展示在图3中，该集合也是算法在图1中的运行结果。

Figure 2. The running process of the algorithm in figure 1

图2. 算法在图1中的运行过程

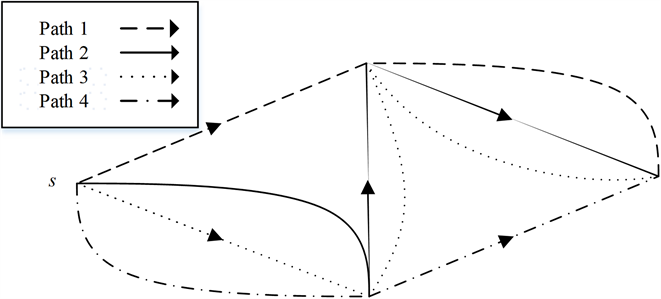
Figure 3. The running result of the algorithm in figure 1

图3. 算法在图1中的运行结果

4. 结论

本文主要针对单平面有向无圈图上的最小路覆盖问题设计了一个时间复杂度为 ${\rm O}\left(nk\right)$ 精确算法，这里n代表图的顶点数、k代表图中最大有向割的边数。由于所考虑的情况是图可以带重边，所以之前最好算法的时间复杂度是 ${\rm O}\left(nm\right)$ ，这里m代表图中边的数目。对于带重边的有向无圈图，其最大有向割中边的数量级要远远小于整个图中边的数量级。该方法是否能够推广到一般有向无圈图的情况仍有待进一步研究。

基金项目

山西省基础研究项目(20210302123097)和山西省自然科学基金(202103021224058)。