基于集成算法的青岛市二手房房价分析与预测

Analysis and Prediction of Second-Hand House Price in Qingdao Based on Integrated Algorithm

摘要: 房地产业关乎国计民生，而二手房交易作为房地产市场的重要组成部分，需要长期、稳定、健康发展。二手房交易过程复杂，这对购房者而言，了解二手房价格显得尤为迫切，同时，二手房价格也是市场监管部门的关注重点。本文利用网络爬虫技术获得“链家”平台2021年度青岛市所有已成交二手房源的相关数据，进行数据预处理后，对比Lasso、随机森林、LightGBM、XGBoost四种模型的预测结果，发现XGBoost模型具有较好的预测优势。由于单一模型的局限性，本文采用Stacking算法进行模型融合，搭建RF-LG-XG模型，预测结果表明本文提出模型的预测效果优于以上单一模型。本文构建二手房价格预测模型为购房者提供了更透明、更准确的参考价格，同时为政府调整政策提供参考，促进房地产市场稳定持续发展。

Abstract: The real estate industry is related to the national economy and the people’s livelihood. As an im-portant part of the real estate market, second-hand housing transactions need long-term, stable and healthy development. The transaction process of second-hand houses is complex, which is par-ticularly urgent for buyers to understand the price of second-hand houses. At the same time, the price of second-hand houses is also the focus of the market supervision department. This paper uses the web crawler technology to obtain the relevant data of all the second-hand houses that have been sold in Qingdao in 2021. Comparing the prediction results of Lasso, random forest, XGBoost and LightGBM, it is found that XGBoost model has better prediction advantages. Due to the limitations of a single model, this paper uses Stacking algorithm for model fusion, and the prediction effect of the RF-LG-XG model is better than the above single model. This paper constructs a second-hand housing price prediction model to provide more transparent and accurate reference prices for home buyers, as well as reference for the government to adjust policies, which is of great practical significance.

1. 引言

房地产一直扮演着推进国民经济发展支柱产业的角色，现如今房地产行业已经有了一个相对成熟的市场体系，带动了相关产业的发展，成为促进经济发展，推进城镇化建设进程的主导力量之一。住房问题不仅影响经济发展，也影响社会稳定。房价的走势一直备受社会关注，习近平总书记在近年来的会议上也多次提到房价，该问题也成为经济等领域的研究热门。随着观念的转变以及结合经济情况，越来越多的人关注二手房。应“一房一价”政策的号召，二手房也根据房产所有者参考市场评估价，结合具体居住情况给出相应的挂牌价格。但二手房的实际成交价格是交易双方协商后达成一致的价格，该价格最能体现市场情况。

本次研究考虑采用问卷调查、实地走访并结合“链家网”上的信息，对青岛2021年的二手房成交价进行研究分析，分析哪些因素是购房者在买房时比较看重的，并提供相应的价格预测模型。由于目前二手房交易市场存在中介商对房屋进行高标价的乱象，扰乱市场秩序，造成不公平的行业交易乱象。本次研究的意义在于可以提供购房者一个比较合理的二手房价格，防止中介商过度溢价。帮助相关政府部门对二手房的房价有一个宏观调控，规范市场秩序，降低二手房交易风险，促进交易双方和谐共赢，推动二手房地产业和谐健康发展。本项研究是具有较强现实意义的。

2. 国内外研究现状

随着我国房地产行业的蓬勃发展，国内许多学者针对房价预测展开研究。李宇琪(2018)，张磊和谢梅(2019)等人 [1] [2] 利用随机森林模型对房价数据进行分析研究，讨论其影响房屋价格的重要因素。王海泉建立不同的房价预测算法模型，并综合比对了模型的预测性能，其中随机森林表现最优 [3] 。张志峰等人使用XGBoost算法对二手房数据进行建模，得到该算法相比于回归模型，具有更好的拟合效果 [4] 。王葛成(2020)针对房地产价格暴涨暴跌问题，采用python语言编写运行BP神经网络模型，预测房地产市场行情，解决买房以及房市投资问题 [5] 。国外也有许多研究成果：Smith T.E.等建立了住房价格趋势的时空模型，详细开发了模型的最大似然估计，进行仿真测试 [6] 。Hong等人在2020年通过对韩国首尔江南区的公寓交易数据进行分析，研究了基于随机森林方法的房价预测器的特点。通过研究，他们证明基于随机森林方法预测器的准确性是非常高的，远远好于基于OLS的预测器 [7] 。E. A. Antipov对使用随机森林模型评估房地产潜在质量进行了首次尝试，研究指出基于随机森林模型的预测准确性最高 [8] 。

3. 数据来源与预处理

3.1. 数据来源

本团队采用问卷调查的方式获取青岛市民在购买二手房时较为感兴趣的问题。首先查阅相关文献，制定合理问卷。其次本团队采用线上和线下两种途径完成问卷派发，共发放1142份并对征集的问卷进行整理筛选，得到有效问卷647份。最后对有效问卷运用统计分析的知识与方法，大致得到青岛市民对于二手房的关注要点，拟定分析问题的相关因素，为团队后续对二手房的发展趋势以及价格预测提供思路。

本文使用的原始数据来源于爬虫技术，爬取青岛“链家网”2021年各市区已成交的二手房信息，包括市南区、市北区、崂山区、李沧区、黄岛区、城阳区、即墨区、胶州市。由于平度区和莱西区在链家网平台2021年没有成交信息，故不做考虑。爬取原始数据共14,804条，其中包括29个变量：楼盘名称、成交时间、区域、子区域、成交价、成交单价、挂牌价格、成交周期、调价、关注、浏览、房屋户型、楼层数、建筑面积、户型结构、套内面积、建筑类型、房屋朝向、建成年代、装修情况、建筑结构、梯户比例、产权年限、配备电梯、交易权属、挂牌时间、房屋用途、房屋年限、房权所属。

3.2. 数据预处理

一般来说，在获得了原始数据之后，不能直接开始进行统计分析等操作。因为通常我们所获得的数据都是脏数据，在分析之前需要对数据进行清洗和预处理，从而提升后续建模的准确率。

3.2.1. 数据清洗

数据清洗在数据分析中发挥着不可或缺的作用，其效果可能会影响后续模型的预测效果。本文做以下处理：

一、将得到的原始数据的多余信息去除，例如：建筑面积45 m²，需要将单位去除。

二、将楼层数从所在楼层分离，得到新的变量“楼层数”。

三、变量值为“-”、未知、暂无数据、NA、NAN等特征值设置为空值。

3.2.2. 变量拓展

借鉴国内外学者对房价研究特别提出的特征价格理论，本文对清洗后数据集进行了相关维度扩展。根据房源的经纬度坐标，本文利用百度地图提供的API接口进行POI爬取，获取了坐标地点附近一定范围内指定配套设施的相关数据。并根据获取到的POI内容，统计出房源位置1000 m范围内有无地铁、公交车站、小学、三甲医院。若有则记为1，无记为0。将该数据集与爬取的数据集合并，作为本次研究的基础数据集。

3.2.3. 缺失值处理

本文将缺失值分为两类，分别为名义型变量缺失值和连续型变量缺失值。针对名义型变量缺失值，我们发现4个变量：房屋年限、配备电梯、建筑类型、户型结构存在缺失值，使用同一楼盘名称的相应数据进行填充。针对连续型变量缺失值，我们发现调价、关注、浏览、建筑面积、套内面积存在缺失值，对该类变量的缺失值，本文采用拉格朗日插值法进行空值插补。

3.2.4. 异常值处理

异常值是指数据中存在明显偏离其他观测值的极端值。箱线图通过数据的分位数，更客观地识别其中的异常点，分位数的耐抗性可以保证箱型图的形状分布不受异常值存在的影响。绘制各数值型变量的箱线图，如图1所示，通过观察发现“成交单价、挂牌价格、建成年代、建筑面积、套内面积”存在极端异常值。其中，成交价、挂牌价格、调价的单位为元/平方；成交单价的单位为万元/平方；成交周期的单位为天数；浏览的单位为人次；建筑面积、套内面积的单位为平方米。

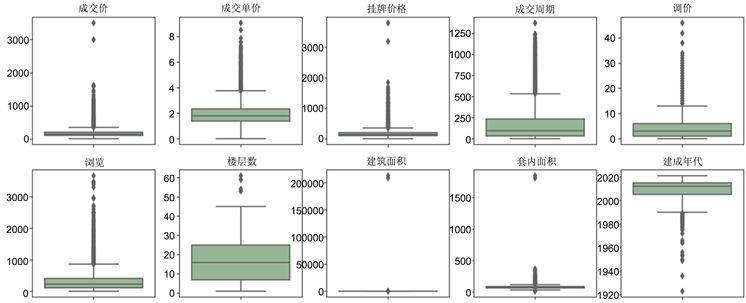
Figure 1. Numerical variable box diagram

图1. 数值型变量箱线图

对上述异常值作如下处理：删除变量“建成年代”中1950年之前的样本数据；删除变量“建筑面积、套内面积”中的极端异常值；由于青岛市的房价跨度较大，上图变量“成交单价”、“挂牌价格”中的异常值在合理价格范围内，因此保留此类异常值。将极端异常值删除后，含有异常值字段的整体分布的偏态情况明显减少，如图2所示。其中，纵坐标表示累积分布值；横坐标的单位分别为万/平方、万元、平方、平方。

3.2.5. 标准化

为了消除指标之间的量纲和取值区间不同的干扰，必须对数据进行标准化处理。本文采用Z-score标准化方法： $x^{\prime }=\left(x-\mu \right)/\sigma$ 。

3.2.6. One-Hot编码

在建模过程中，当自变量的类型为定性变量时，需要将定性数据设置成哑变量。本团队使用Python软件pandas库中的get_dummies()函数进行one-hot编码。以户型结构为例，其类别分别为平层、错层、复式、跃层，使用one-hot编码得到。为了后续建模，我们将区域、房屋户型、房屋朝向、户型结构、建筑类型、装修情况、配备电梯、房屋用途、房权所属处理为上述哑变量，具体处理如表1所示。

4. 模型介绍

4.1. XGBoost模型

极端梯度提升(XGBoost)，该算法是基于梯度提升(Gradient Boosting)，对其进行改进和优化，属于串行生成的集成学习中的一类 [9] 。XGBoost最后的输出结果是一个加性模型的形式，即：

${\hat{y}}_i={\displaystyle \underset{k=1}{\overset{K}{\sum }}{f}_k}\left(x_i\right),f_k\in F$ (1)

其中F表示所有回归树的函数空间，k为树的总个数， $f_k\left(x_i\right)$ 为第k颗树对样本 $x_i$ 的预测结果， ${\hat{y}}_i$ 为样本 $x_i$ 的预测结果。

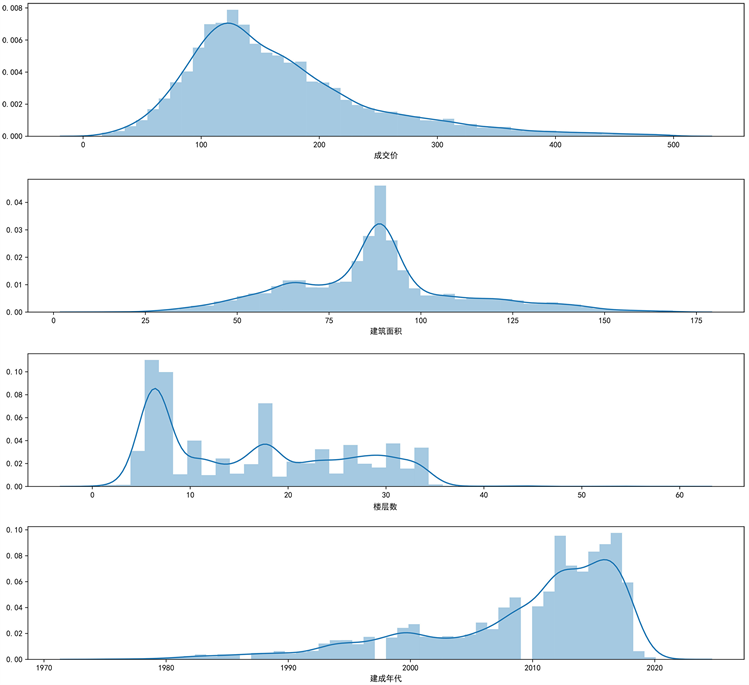
Figure 2. Characteristic distribution after deleting outliers

图2. 删除异常值后特征分布图

Table 1. One-hot coding example

表1. One-hot编码示例

与一般的机器学习问题类似，为了评估这个输出结果，需要考虑特定的损失函数，假定为l；为了防止过拟合，采用结构风险最小化策略，于是我们的目标是最小化：

$L\left(f_k\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}l\left(y_i,{\hat{y}}_i\right)}+{\displaystyle \underset{k=1}{\overset{K}{\sum }}\Omega \left(f_k\right)}$ (2)

其中l为损失函数，用来表示预测值与实际值之间的差异，即样本 $x_i$ 的训练误差。第二项中 $\Omega \left(f_k\right)$ 表示第k棵树的正则项，用来惩罚模型的复杂度。

考虑到加性模型，利用前向分步算法每次贪婪的学习一颗决策树并惩罚，所以当进行第t次迭代时，第 $t-1$ 棵树已经训练完成，此时前面 $t-1$ 棵树的训练误差和正则项全部为确定的常数项，此时最小化的目标函数就变成了：

$\begin{array}{c}L\left(f_k\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}l\left(y_i,{\hat{y}}_i\right)}+{\displaystyle \underset{k=1}{\overset{K}{\sum }}\Omega \left(f_k\right)}\\ ={\displaystyle \underset{i=1}{\overset{n}{\sum }}l\left(y_i,{\hat{y}}_i{}^{\left(t-1\right)}+f_t\left(x_i\right)\right)}+\Omega \left(f_k\right)+constant\end{array}$ (3)

所以现在的目标就是，找出一个 $f\left(t\right)$ 使得目标函数最小。XGBoost利用了目标函数的二阶信息。这类似于牛顿法使用二次函数进行逼近，由于二次函数具有极值点，因此可以明确的给出在一次逼近中的最优值在哪里。XGBoost具有以下优点：

1) XGBoost考虑到了模型的复杂度，加入了正则项，具有较好的泛化能力。

2) 高效可扩展，能够处理大规模数据。

3) 鲁棒性强，与深度学习模型相比，不需要准确的参数调整也可取得较近的效果。

4.2. 模型融合

模型融合的本质是根据特定方法对于多个单一模型的预测结果进行组合，从而提高预测精度。本文思考是否可以通过模型融合进一步提升机器学习的性能并加强模型的准确度，更好的投入到实际的应用中。模型融合的方法包括Voting、Averaging、Stacking、Boosting和Bagging。其中Voting适合分类问题，Averaging适合回归问题，Stacking等算法是基于前两者的改进，本文选取Stacking算法进行模型融合。

Stacking算法的本质是一种分层结构，层数可以是二、三或者更多，在解决实际问题时，一般选择两层结构。该算法的步骤包括：首先利用第一层的学习器对原始数据进行训练，把该层的输出结构作为训练集进行第二层的训练。进行Stacking集成需要基学习器尽量保持独立，结合了不同学习器之间的多样性。为了使模型更加稳健，采用多折交叉验证。模型融合的流程图如图3所示。

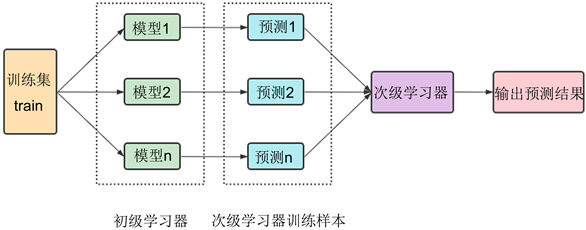
Figure 3.Stacking model fusion framework

图3. Stacking模型融合框架

5. 实验结果

5.1. 性能度量指标

假设预测值为 $y=\left\{{\hat{y}}_1,{\hat{y}}_2,\cdots ,{\hat{y}}_n\right\}$ ，真实值为 $y=\left\{y_1,y_2,\cdots ,y_n\right\}$ 。

1) MAE (Mean Absolute Error)，即平均绝对值误差，它表示预测值和实际观测值之间绝对误差的平均值。MAE较MSE优化了正负误差相互抵消的问题，可以更准确地反映实际预测误差。其计算方法如下：

$\text{MAE}=\frac{{\displaystyle {\sum }_{i=1}^n\left|{\hat{y}}_i-y_i\right|}}{n}$ (4)

2) MSE (Mean Square Error)，即均方误差，它是真实值与预测值的差值的平方和的平均。由于平方的关系，负值不会抵消正值，还会放大误差的影响。由于平方形式便于求其导函数的优势，故均方误差常被用作线性回归的损失函数。

$\text{MSE}=\frac{{\displaystyle {\sum }_{i=1}^n{\left({\hat{y}}_i-y_i\right)}^2}}{n}$ (5)

3) MAPE (Mean Absolute Percent Error)，即平均绝对误差百分比，以百分比来衡量误差的大小。这是个相对值，而不是绝对值。故它常被用来进行对不同模型同一组数据的评估，对同一组数据，模型给出MAPE小的模型比较好。

$\text{MAPE}=\frac{100\%}{n}{\displaystyle {\sum }_1^n\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|}$ (6)

4) R²：决定系数代表可以由自变量X表示的因变量Y的差异，即输出量Y可以被输入量X解释的百分比。其计算方法如下：

$R^2=\frac{\text{SSR}}{\text{SST}}=1-\frac{\text{SSE}}{\text{SST}}$ (7)

其中 $\text{SSE}={\displaystyle {\sum }_i{\left(y_i-{\hat{y}}_i\right)}^2}$ ， $\text{SSR}={\displaystyle {\sum }_i{\left({\hat{y}}_i-{\bar{y}}_i\right)}^2}$ ， $\text{SST}=\text{SSR}+\text{SSE}={\displaystyle {\sum }_i{\left(y_i-{\bar{y}}_i\right)}^2}$ 。

5.2. XGBoost模型

采用XGBoost模型进行建模分析与预测时，需要对函数中的参数进行调优处理选择最优的参数进行建模运行。选择gridSearchCV方法对XGBoost模型的各项参数进行调优，以寻求最适合模型的参数值。选取以下几个参数进行调优并绘制参数和r²的学习曲线图，便于确定参数 [10] 。

1) 确定num_round参数的选择范围，绘制num_round和r²的学习曲线，如图4所示，横坐标为num_round的数值，纵坐标为相对应的r²。选择使准确度尽可能高的情况下的num_round值。由下图所示，num_round选择600左右的值较为合理。

Figure 4. Learning curve of num_round and r²

图4. num_round和r²的学习曲线图

2) Booster参数中的eta参数，该参数代表的是模型学习速率，主要用于控制树的权重，避免出现过拟合现象。对eta参数值进行调优，考虑模型的迭代次数。绘制eta和r²的学习曲线，如图5所示，横坐标表示eta的参数值，纵坐标为相应的r²。由图可以看出eta的值在达到0.05左右时r²的准确率将会达到0.8349，eta在增大，r²的准确率将保持稳定，故选择eta = 0.05。

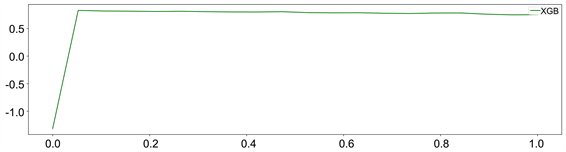
Figure 5. Learning curve of eta and r²

图5. eta和r²的学习曲线图

3) Booster参数中的subsample参数，该参数表示每棵树随机采样的比例。绘制subsample和r²学习曲线，如图6所示，横坐标表示subsample的参数值，纵坐标为相应的r²。subsample的值在达到0.05左右时r²的准确率将保持不变。

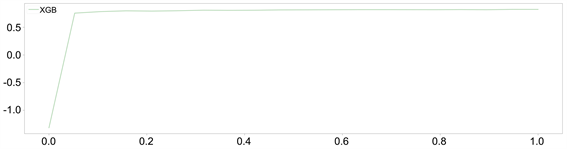
Figure 6. Learning curve of subsample and r²

图6. subsample和r²的学习曲线图

4) 其余参数我们不做修改，保持函数内置的默认值。用xgb自带的网格搜索进行调参，绘制对比图，如图7所示，横坐标表示模型的均方误差，纵坐标表示参数树的最大深度，此处是进行一个“剪枝”操作，防止模型过拟合。

Figure 7. Comparison before and after parameter adjustment

图7. 调参前后对比图

由上图可看出，与初始默认参数相比，经过参数优化后的模型获得了更好的泛化能力且模型的均方误差下降。调参后的XGBoost模型准确率，如表2所示，分析下表可以看出，参数调优后的模型对整体预测准确率有一定的提升。

Table 2. Model accuracy after XGBoost parameter adjustment

表2. XGBoost调参后模型准确率

5.3. 多个模型比较

分别建立Lasso、随机森林、LightGBM、XGBoost模型，并比较四种模型在测试集上的表现效果，如表3所示。

Table 3. Accuracy of different models on the test set

表3. 不同模型在测试集上的准确率

分析这四种评价指标，一般认为R²越大效果越好，MSE、MAE、MAPE越小越好，将每个指标的最优值用下划线表示。综合各个评价指标，本文认为在XGBoost模型预测效果最优。该模型的R²达到了0.84，我们可以认为该模型达到了理想预期。

5.4. 特征重要性分析

比较前面章节所建立的模型，我们发现XGBoost模型对二手房房价预测的效果好，准确率也较高。建立XGBoost模型的过程中，利用Python软件得到特征的重要性得分，排名为前20的变量如图8所示。可以直观地看出区域位置对房价影响重大；其次，楼层数以及二手房的房间数也是购房者关注的重点。

5.5. Stacking模型融合

前文中比较了多个单一模型的预测准确度，并对模型进行参数调优后准确度有所提升，其中XGBoost模型的参数调优后预测准确度最高。比较参数调优前后，发现模型的准确度提升的幅度较小，接下来考虑通过stacking模型融合的方法进一步提升预测准确度。

首先利用Stacking算法对随机森林、LightGBM模型、XGBoost模型进行模型融合得到RF-LB-XG模型，新模型有较好的稳健性。利用该模型对测试集进行检验，检验结果如表4所示。

Figure 8. XGBoost feature importance ranking

图8. XGBoost特征重要性排序

Table 4. Accuracy of RF-LB-XG model

表4. RF-LB-XG模型准确率

通过上表可以看出RF-LB-XG模型在测试集上相较之前的模型有更好的表现，R²在测试集上的达到了0.8402，在训练集上为0.9486，一定程度上避免了过拟合问题。

由于数据量较大，这里只选取了其中一段预测做可视化展示，如图9所示。其中，纵坐标表示房屋成交价格（万）；横坐标是预测的样本编号。该图可以更加直观的看出RF-LB-XG模型表现更加优异。红色带*的线是真实值，蓝色带×的线是RF-XG-LB模型，可以看出该线相较于其他模型的预测拟合值线更加贴近真实值结果。

Figure 9. Forecast chart of each model

图9. 各模型预测图

6. 结论

本团队对青岛市二手房的市场价格等问题进行研究，首先通过爬虫技术爬取青岛市2022年份二手房成交的共14804条房屋信息，并根据经纬度连接百度API进行POI爬取，得到坐标地点附近一定范围内指定配套设施的相关数据。

接下来进行数据预处理，通过数据清洗、缺失值处理、异常值处理等手段得到后续分析所需的数据；研究房价的预测建模，通过搭建Lasso回归模型、随机森林模型、LightGBM模型、XGBoost模型这四种模型对二手房价格进行建模分析处理。根据建模预测结果发现，XGBoost模型的预测效果最佳，MSE仅为0.0046。另外得到的特征的重要性排序，最终得到影响房价的重要因素，用于后续房价的分析与预测。根据得到的各个因素的重要程度分析，发现建筑面积、区域、楼层数对二手房价格的影响程度较大，这表明，青岛市购房者在购买二手房时，这些因素的不同会造成房价的较大差异。这也反映了购房者在购房时对此类因素的重视程度较大，从而影响房价。最后，考虑利用Stacking算法进行模型融合，对比发现融合模型RF-XG-LB的泛化能力更强，在测试集上的MSE为0.0045，预测效果优于单一模型。通过本篇文章的建模分析，借助模型可以根据购房者的购房需求预测得到符合需求的二手房成交价格的大致区间，为购房者的购房决策提供合理建议；另外也为政府的调控政策提供参考依据。

基金项目

山东省自然科学基金青年项目(ZR2021QA053)。

NOTES

^*通讯作者。