波浪能发电装置输出功率的微分方程模型

doi:10.12677/AAM.2023.124176

期刊菜单

波浪能发电装置输出功率的微分方程模型
The Differential Equation Model for the Out-put Power of Wave Energy Converter

DOI: 10.12677/AAM.2023.124176, PDF, HTML, XML,
作者: 马家耀, 吴彬睿：杭州师范大学经亨颐教育学院，浙江杭州；吕平^*：杭州师范大学数学学院，浙江杭州
关键词: 微分方程；多重搜索法；波浪能发电装置；阻尼系数；Differential Equation； Multiple Search Algorithms； Wave Energy Converter； Damping Factor

摘要: 波浪能是当今社会一种十分具有前景的清洁可再生能源，提高波浪能发电装置的转化效率尤为重要。针对波浪能发电装置只做垂荡运动的情况，本文建立基于微分方程的垂荡模型。以垂荡模型为基础，本文进一步计算波浪能发电装置的平均输出功率，并建立以波浪能发电装置平均输出功率最大为目标的最优阻尼系数模型。最后，本文通过多重搜索算法，遍历求解得到最大输出功率及对应的最优阻尼系数。

Abstract: Nowadays wave energy as the clean and renewable energy resource has a promising future, so it is particularly significant to enhance the conversion efficiency of wave energy converter. Aiming at the situation that the wave energy converter only does vertical motion, this paper establishes a vertical oscillation model based on differential equation. In terms of this model, the paper further calculates the average output power of wave energy converter, and establishes an optimal damping coefficient model with the goal of the maximum average output power. Finally, the maximum output power and the corresponding optimal damping factor are obtained by traversing the solution through multiple search algorithms.

文章引用：马家耀, 吴彬睿, 吕平. 波浪能发电装置输出功率的微分方程模型[J]. 应用数学进展, 2023, 12(4): 1698-1703. https://doi.org/10.12677/AAM.2023.124176

1. 引言

现今，人类面临能源需求和环境污染的双重挑战，发展可再生能源产业已成为共识。世界波浪能资源储量约29,000 TW [1] ，具有巨大的开发利用潜力；我国波浪能储能约1.6 × 10⁷ kW [2] ，具备规模化开发利用条件 [3] 。因此，波浪能作为一种重要的海洋可再生能源，具有可观的应用前景，有望成为缓解能源短缺的重要能量来源。

波浪能发电装置(wave energy converter, WEC)的能量转换效率是波浪能规模化利用的关键问题之一。本文主要解决特定情况下的波浪能装置输出功率问题，即浮子在波浪中仅做垂荡运动，且阻尼系数与浮子和振子的相对速度的绝对值的幂成正比。

本文分别建立了基于微分方程的垂荡模型与基于单目标优化的最优阻尼系数模型，利用数值法中的有限差分法和多重搜索算法进行求解，给出了波浪能发电装置的运动情况以及能够达到最大PTO系统输出功率的阻尼系数。

2. 模型的构建

2.1. 垂荡模型

2.1.1. 垂荡位置坐标与垂荡位移

为了定量描述浮子与振子的运动状态， $x_{M} (t)$ 表示浮子t时刻的垂荡位置坐标， $x_{m} (t)$ 表示振子t时刻的垂荡位置坐标。并且本文选定如下一维坐标系，竖直向上为正方向，以海平面对应的点o作为原点，同时规定初始时刻为 $t = 0$ 时刻，波浪能装置初始状态情况如图1所示。

Figure 1. Schematic diagram of the initial moment of WEC

图1. 波浪能发电装置初始时刻示意图

图中， $h_{1} = 0.8 m$ ， $h_{2} = 3.0 m$ ， $h_{3} = 0.5 m$ ， $x_{M}^{0}$ 为浮子初始时刻的垂荡位置坐标，即 $x_{M}^{0} = x_{M} (0)$ ； $x_{m}^{0}$ 为振子初始时刻的垂荡位置坐标，即 $x_{m}^{0} = x_{m} (0)$ 。已知初始时刻浮子与振子平衡于静水中，因此根据经典力学相关知识建立一下方程组，并求解 $x_{M}^{0}$ 及 $x_{m}^{0}$ ：

$(m + M) g = ρ g (V_{锥} + S_{0} | x_{M}^{0} |)$

$V_{锥} = \frac{1}{3} S_{0} h_{1}$

$m g = k | (x_{m}^{0} - x_{M}^{0} - l_{0}) |$

其中，M = 4866 kg表示浮子的质量，m = 2433 kg表示振子的质量，l₀ = 0.5 m代表弹簧原长，k = 80,000 N/m代表弹簧刚度， $ρ = 1025 kg / m^{3}$ 为海水密度，S₀ = πm²为圆锥底面积，h₁ = 0.8 m为圆锥部分高度。易求得：

${\begin{cases} x_{M}^{0} = - 2.0 \\ x_{m}^{0} = - 1.8 \end{cases}$

假设 $X_{M} (t)$ 为浮子0至t时刻的垂荡位移， $X_{m} (t)$ 为振子0至t时刻的垂荡位移。由位置坐标与位移的关系可得，

$X_{M} (t) = x_{M} (t) - x_{M} (0) = x_{M} (t) - x_{M}^{0}$

$X_{m} (t) = x_{m} (t) - x_{m} (0) = x_{m} (t) - x_{m}^{0}$

2.1.2. 浮子与振子受力分析

浮子在波浪中仅做垂荡运动，即仅考虑浮子的一维直线运动。浮子的受力情况是复杂的，需要考虑浮子重力、附加惯性力、兴波阻尼力F_r、浮力F_b、波浪激励力F_e、弹簧弹力F_s以及直线阻尼器施加的阻尼力F_d；振子的受力情况相对简单，只需考虑自身重力、弹簧弹力F_s以及阻尼力F_d。

波浪激励力F_e：由题设知，波浪激励力是一个周期力，呈现周期变化的特点，且 $F_{e} = f \cos ω t$ 。式中f = 4089 N为波浪激励力振幅，ω = 2.2143 s⁻¹为入射波浪频率。

弹簧弹力F_s：假设弹簧满足胡克定理，即弹簧弹力与长度变化量成线性关系， $F_{s} = λ_{s} (x_{m} (t) - x_{M} (t) - l_{0})$ 。式中 $λ_{s} = 80000 N / m$ 为弹簧刚度，l₀ = 0.5 m为弹簧原长。

阻尼力F_d：直线阻尼器施加的阻尼力与浮子与振子的相对速度成正比，直线阻尼器的阻尼系数 $λ_{d} = α {| v_{M} (t) - v_{m} (t) |}^{β}$ ，其中，比例系数为 $α$ 且 $α \in [0, 100000]$ ，幂指数为 $β$ 且 $β \in [0, 1]$ 。因此， $F_{d} = λ_{d} (v_{m} (t) - v_{M} (t))$ 。式中 $v_{m} (t)$ 为振子t时刻的垂荡速度， $v_{M} (t)$ 为浮子t时刻的垂荡速度。

兴波阻尼力F_r：浮体在海水中做垂荡运动时，会兴起波浪，从而产生对浮体摇荡运动的阻力，称为兴波阻尼力。由于仅考虑浮体的垂荡运动，因此兴波阻尼力F_r与垂荡运动的速度成正比，方向相反，比例系数为兴波阻尼系数 $λ_{r} = 167.8395 N \cdot S / m$ ， $F_{r} = λ_{r} v_{M} (t)$ 。

浮力F_b：浸在流体内的物体受到流体竖直向上的作用力叫做浮力， $F_{b} = ρ g V_{p}$ 。式中 $ρ$ 为海水密度，g = 9.8 m/s²为重力加速度，V_p为排开液体体积。 $V_{p} = V_{p} (t)$ 是一个与时间有关的函数，并且考虑到波浪能装置底部的圆锥部分是否露出水面，可以得到 $V_{p} (t)$ 为如下分段函数：

$V_{p} (t) = {\begin{array}{l} V_{锥} + S_{0} | x_{M} (t) |, & x_{M} (t) \leq 0 \\ {(\frac{h_{1} - x_{M} (t)}{h_{1}})}^{3} V_{锥}, & x_{M} (t) \geq 0 \end{array}$

附加惯性力F_add：微幅波推动浮体做摇荡运动的力不仅要推动浮体运动，还要推动浮体周围的流体运动。因此，要使浮体在海水中获得加速度，需要施加额外的力，称为附加惯性力F_add。附加惯性力对应产生一个虚拟质量，即附加质量m_add。对于该附加质量m_add，考虑其受到的浮力 ${F^{'}}_{b}$ ，可以认为 ${F^{'}}_{b} = m_{a d d} g$ 。

静水恢复力F_q：浮体在海水中做垂荡运动时，会受到使浮体回到平衡位置的作用力，称为静水恢复力F_q。静水恢复力本质为重力与浮力的合力，因此本文考虑重力与浮力，而非静水恢复力。

2.1.3. 垂荡模型的建立

根据上文的受力分析，基于牛顿经典力学可以得到以下力学方程：

$(M + m_{a d d}) {\dot{v}}_{M} (t) = - (M + m_{a d d}) g + F_{s} + F_{d} + F_{b} + {F^{'}}_{b} + F_{e} - F_{r}$

$m {\dot{v}}_{m} (t) = - m g - F_{s} - F_{d}$

又考虑到 ${F^{'}}_{b} = m_{a d d} g$ 可以得到

$(M + m_{a d d}) {\dot{v}}_{M} (t) = - M g + F_{s} + F_{d} + F_{b} + F_{e} - F_{r}$

$m {\dot{v}}_{m} (t) = - m g - F_{s} - F_{d}$

再根据位移与速度的关系得：

${\dot{X}}_{M} (t) = v_{M} ( t )$

${\dot{X}}_{m} (t) = v_{m} ( t )$

综上分析，可以得到如下基于微分方程组的垂荡运动模型：

${\begin{cases} {\dot{v}}_{M} (t) = \frac{- M g + F_{s} + F_{d} + F_{b} + F_{e} - F_{r}}{M + m_{a d d}} \\ {\dot{v}}_{m} (t) = \frac{- m g - F_{s} - F_{d}}{m} \\ {\dot{X}}_{M} (t) = v_{M} (t) \\ {\dot{X}}_{m} (t) = v_{m} ( t ) \end{cases}$

由微分方程解的存在唯一性定理可知，以上微分方程组存在唯一解，但是考虑到 $v_{M} (t), v_{m} (t), X_{M} (t), X_{m} (t)$ 难以求解其具体表达式，因此文本采用数值方法中的有限差分法，选取合适的步长∆t，将其离散化处理得到以下有限差分方程组：

${\begin{cases} v_{M} (t_{i + 1}) = {\dot{v}}_{M} (t_{i}) Δ t + v_{M} (t_{i}) \\ v_{m} (t_{i + 1}) = {\dot{v}}_{m} (t_{i}) Δ t + v_{m} (t_{i}) \\ X_{M} (t_{i + 1}) = v_{M} (t_{i + 1}) Δ t + X_{M} (t_{i}) \\ X_{m} (t_{i + 1}) = v_{m} (t_{i + 1}) Δ t + X_{m} (t_{i}) \\ t_{i} = i \cdot Δ t \end{cases}$

有限差分法的数值解可以作为微分方程的近似数值解，解的误差与步长∆t的选取直接相关，∆t越小，结果误差越小，因此在条件允许的情况下，∆t越小越好，文选取∆t = 0.01 s，根据有限差分方程组中的迭代关系，即可求得一系列离散时刻的垂荡位移与垂荡速度。

2.2. 最优阻尼系数模型

在微幅波的作用下，浮子运动并带动振子运动，通过两者的相对运动驱动阻尼器做功，并将所做功作为能量输出。

本文以垂荡模型为基础，考虑 $P = F v$ 得到PTO系统的瞬时输出功率 $P (t) = F_{d} (t) (v_{M} (t) - v_{m} (t))$ 那么波浪能装置的平均输出功率 $\bar{P}$ 也随之而出，

$\bar{P} = \frac{\int_{0}^{t} P (ξ) d ξ}{t} = \frac{\sum_{i = 0}^{n} P (t_{i}) Δ t}{n Δ t}$

其中n∆t为总时长。目标使平均输出功率 $\bar{P}$ 最大，从而建立如下单目标优化模型，

$\max \bar{P}$

${\begin{cases} λ_{d} = α {| v_{M} (t_{i}) - v_{m} (t_{i}) |}^{β} \\ v_{M} (t_{i + 1}) = {\dot{v}}_{M} (t_{i}) Δ t + v_{M} (t_{i}) \\ v_{m} (t_{i + 1}) = {\dot{v}}_{m} (t_{i}) Δ t + v_{m} (t_{i}) \\ X_{M} (t_{i + 1}) = v_{M} (t_{i + 1}) Δ t + X_{M} (t_{i}) \\ X_{m} (t_{i + 1}) = v_{m} (t_{i + 1}) Δ t + X_{m} (t_{i}) \\ t_{i} = i \cdot Δ t \end{cases}$

3. 模型的求解

本文选取一段足够长的时间计算平均输出功率以减少误差，总时长n∆t为40个波浪周期，其中∆t = 0.01 s。模型中主要含有比例系数 $α$ 与幂指数 $β$ 两个变量，本文采用多重搜索算法同时对 $α$ 与 $β$ 进行搜索。

3.1. 初步搜索

选取步长 $Δ α = 1000$ 、 $Δ β = 0.1$ ，进行遍历求解最佳取值范围，结果如图2所示。此时， $α \in [98000, 100000]$ 且 $β \in [0.40, 0.42]$ 时，平均输出功率较大。

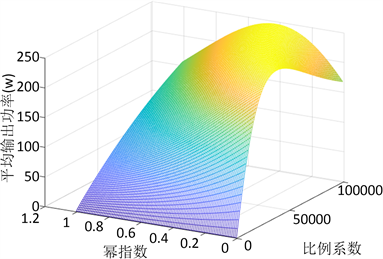
Figure 2. Surface plot of average output power—preliminary search

图2. 平均输出功率变化曲面图——初步搜索

3.2. 精确搜索

选取步长 $Δ α = 100$ 、 $Δ β = 0.001$ ，进一步搜索，结果如图3所示。此时，最优比例系数100,000且 $β = 0.416$ 。

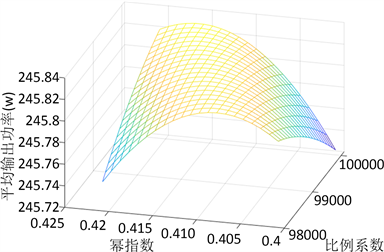
Figure 3. Surface plot of average output power—precise search

图3. 平均输出功率变化曲面图——精确搜索

4. 结论

海洋蕴含着丰富的资源，其中波浪能尤为突出 [4] ，并且，随着波浪能发电相关技术的发展，海洋波浪能有望为解决能源短袖、生态环境等问题做出巨大贡献 [5] 。本文给出了某种波浪能装置的最优阻尼系数设计方案，也就是阻尼系数与浮子与振子的相对速度的绝对值的幂成正比的情况，即 $λ_{d} = α {| v_{M} (t) - v_{m} (t) |}^{β}$ ，且满足 $α \in [0, 100000]$ ， $β \in [0, 1]$ 。

最终得到，当 $α = 100000$ ， $β = 0.416$ 时，波浪能发电装置PTO系统的平均输出功率最大，为245.84 W。

参考文献

[1]	Mork, G., Barstow, S., Pontes, M.T., et al. (2010) Assessing the Global Wave Energy Potential. Proceedings of the 29th International Conference on Ocean, Offshore Mechanics and Arctic Engineering, Shanghai, 6-11 June 2010, 447-454. https://doi.org/10.1115/OMAE2010-20473
[2]	王项南, 贾宁, 薛彩霞, 等. 关于我国海洋可再生能源产业化发展的思考[J]. 海洋开发与管理, 2019, 36(12): 14-18.
[3]	刘艳娇, 彭爱武, 黄铭冶. 海洋波浪能发电装置PTO系统研究进展[J/OL]. 太阳能学报: 1-13, 2023-03-21.
[4]	王立国, 游亚戈, 张亚群, 等. 波浪能发电装置动力摄取系统研究进展[J]. 机床与液压, 2013, 41(1): 165-168+162.
[5]	刘延俊, 武爽, 王登帅, 等. 海洋波浪能发电装置研究进展[J]. 山东大学学报(工学版), 2021, 51(5): 63-75.

为你推荐

友情链接