特殊图类的非正常染色

Improper Coloring of the Special Graphs

摘要: 设k，l是非负整数，图G的一个非正常(k, l)-染色是指用红蓝2种颜色对顶点集V(G)进行着色，使得对每一个染以红色(或蓝色)的点，至多k (或l)个邻点与其染色相同。本文主要研究路和圈的平方图的非正常(k, l)-染色。

Abstract: Let k, l be two non-negative integers. An improper (k, l)-coloring of a graph G refers to color the vertex set of V(G) with two colors, such that for each vertex with color red (or blue) has at most k (or l) neighbors of the same color with it. This paper focuses on improper (k, l)-coloring of square graphs of paths and cycles.

1. 预备知识

图论起源于现实世界，它的思想的传承起源于一些民间广泛流传的古老数学游戏和趣题的研究。图的染色问题是图论中非常重要的研究课题之一，它来源于著名的“四色问题”，即任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。

定义1 [1] $V\left(G\right)$ 和 $E\left(G\right)$ 分别表示图G的点和边的集合。图 $G^{\prime }$ 称为图G的子图，满足 $V\left(G^{\prime }\right)\subseteq V\left(G\right)$ ， $E\left(G^{\prime }\right)\subseteq E\left(G\right)$ 。设 $V^{\prime }$ 是V的一个非空子集。以 $V^{\prime }$ 为顶点集，以两端点均在 $V^{\prime }$ 中的边为全体边集构成的子图，称为G的由 $V^{\prime }$ 导出的子图，记为 $G\left[V^{\prime }\right]$ 。

定义2 [1] 设 $d_1,\cdots ,d_k$ 是k个非负整数，图G称为是非正常 $\left(d_1,\cdots ,d_k\right)$ -可染的，或 $\left(d_1,\cdots ,d_k\right)$ -可染的，当且仅当G的点集可以被划分为 $V_1,\cdots ,V_k$ ，使得每个点导出子图 $G\left[V_i\right]$ 都满足 $\Delta G\left[V_i\right]\le d_i$ ，也就是说，对任意的 $v\in V\left(G\left(V_i\right)\right)$ ，v在 $G\left[V_i\right]$ 中至多 $d_i$ 个邻点， $1\le i\le k$ 。当 $d_1=\cdots =d_k=0$ 时，即为正常染色。 $\chi \left(G\right)$ 表示使G为k可着色的数k的最小值。

定义3 [2] 令 $x,y\in V\left(G\right)$ ，G中所有从x到y的路的最短长度称为从x到y的距离记为 $d_G\left(x,y\right)$ 。图G的平方图G²定义为：图G²与G有相同的点集，图G²中的两顶点为邻点当且仅当在图G中与此两点对应点的距离小于等于2。

定义4 [3] 设 $P_n=v_1{v}_2\cdots v_n$ 是一条长为n的路，当且仅当 $P_n$ 上两点的距离为2时增加一条边，这样所得到的图叫做 $P_n^2\left(v_1,v_n\right)$ ，简记为 $P_n^2$ 。设 $C_n=v_1{v}_2\cdots v_n{v}_1$ 是一个长为n的圈，当且仅当两点的距离为2时增加一条边，这样所得到的图叫做 $C_n^2\left(v_1,v_n\right)$ ，简记为 $C_n^2$ 。

关于路和圈的平方图的正常染色结果如下。

引理 [2] 对于任意的圈，有如下结论成立：

$\{\begin{array}{l}\chi \left(P_n^2\right)=3\left(n\ge 3\right)\\ \chi \left(C_5^2\right)=5\\ \chi \left(C_{3n}^2\right)=3\\ \chi \left(C_{3n+1}^2\right)=4\\ \chi \left(C_{3n+2}^2\right)=4\left(n\ge 2\right)\end{array}$

根据上述引理，我们将考虑降低色数为2，即用2种颜色对路和圈的平方图进行非正常染色，证明这两种平方图分别满足特定的非正常染色方式(下文将具体给出定理与证明)。

2. 结论与证明

定理1 $P_n^2\left(n\ge 3\right)$ 是 $\left(1,1\right)$ -可染的。

证明：设 $P_n=v_1{v}_2\cdots v_n\left(n\ge 3\right)$ 。考虑 $P_n$ 中的三个连续的点 $v_{i-1}$ ， $v_i$ ， $v_{i+1}$ ，根据平方图的定义，在 $P_n^2$ 中此三点相互邻接。现对 $P_n^2$ 进行如下染色c：

对 $1\le i\le n$ ，当 $i=0\left(\mathrm{mod}4\right)$ 或 $i=1\left(\mathrm{mod}4\right)$ 时，令 $c\left(v_i\right)=1$ ；当 $i=2\left(\mathrm{mod}4\right)$ 或 $i=3\left(\mathrm{mod}4\right)$ 时，令 $c\left(v_i\right)=2$ 。

根据上述染色， $c\left(v_2\right)=c\left(v_3\right)=2$ ， $c\left(v_1\right)=1$ ， $c\left(v_4\right)=1$ (若存在 $v_4$ )，即 $v_1$ 的所有邻点与其染色不同，与 $v_2$ 染相同颜色的邻点只有 $v_3$ (如图1所示)。我们将逐个考察 $v_n$ ， $v_{n-1}$ 及 $v_i$ ( $3\le i\le n-2$ )，并说明在上述染色方式下，至多一个邻点与其染色相同。首先考虑 $v_n$ 和 $v_{n-1}$ 。当 $i=0\left(\mathrm{mod}4\right)$ 时，根据上面的染色方式， $c\left(v_n\right)=1$ ， $c\left(v_{n-1}\right)=c\left(v_{n-2}\right)=2$ ， $c\left(v_{n-3}\right)=1$ ，即 $v_n$ 与 $v_{n-1}$ ， $v_{n-2}$ 均染不同颜色，与 $v_{n-1}$ 染相同颜色的点只有 $v_{n-2}$ (如图1所示)；当 $i=1\left(\mathrm{mod}4\right)$ 时，根据上面的染色方式， $c\left(v_n\right)=c\left(v_{n-1}\right)=1$ ， $c\left(v_{n-2}\right)=c\left(v_{n-3}\right)=2$ ，即与 $v_n$ 染相同颜色的邻点只有 $v_{n-1}$ ， $v_{n-1}$ 的所有邻点中仅 $v_n$ 与其染色相同；类似地，当 $i=2\left(\mathrm{mod}4\right)$ 时，有 $c\left(v_n\right)=\left(v_{n-3}\right)=2$ ， $c\left(v_{n-1}\right)=c\left(v_{n-2}\right)=1$ ；当 $i=3\left(\mathrm{mod}4\right)$ 时，有 $c\left(v_n\right)=c\left(v_{n-1}\right)=2$ ， $c\left(v_{n-2}\right)=1$ ， $c\left(v_{n-3}\right)=1$ (若 $v_{n-3}$ 存在，即 $n>3$ )，无论哪种情况，至多一个邻点与 $v_n$ (或 $v_{n-1}$ )染色相同。

接下来考虑 $v_i$ ， $3\le i\le n-2$ 。当 $i=0\left(\mathrm{mod}4\right)$ 时，根据上面的染色方式， $c\left(v_i\right)=c\left(v_{i+1}\right)=1$ ， $c\left(v_{i-1}\right)=c\left(v_{i-2}\right)=c\left(v_{i+2}\right)=2$ ，即 $v_i$ 与 $v_{i-1}$ ， $v_{i-2}$ ， $v_{i+2}$ 均染不同颜色，与 $v_i$ 染相同颜色的点只有 $v_{i+1}$ (如图1所示)；当 $i=1\left(\mathrm{mod}4\right)$ 时，根据上面的染色方式， $c\left(v_i\right)=c\left(v_{i-1}\right)=1$ ， $c\left(v_{i+1}\right)=c\left(v_{i-2}\right)=c\left(v_{i+2}\right)=2$ ，即与 $v_i$ 染相同颜色的邻点只有 $v_{i-1}$ ；类似地，当 $i=2\left(\mathrm{mod}4\right)$ 时，有 $c\left(v_i\right)=c\left(v_{i+1}\right)=2$ ， $c\left(v_{i-1}\right)=c\left(v_{i-2}\right)=c\left(v_{i+2}\right)=1$ ；当 $i=3\left(\mathrm{mod}4\right)$ 时，有 $c\left(v_i\right)=c\left(v_{i-1}\right)=2$ ， $c\left(v_{i+1}\right)=c\left(v_{i-2}\right)=c\left(v_{i-3}\right)=1$ 。无论哪种情况，至多一个邻点与 $v_i$ 染色相同。

综合以上情况，定理结论成立。

Figure 1. Improper (k, l)-coloring of square graphs of paths

图1. 路的平方图的非正常染色

定理2 1) 若 $n\equiv 0\left(\mathrm{mod}3\right)$ ，则 $C_n^2$ 是 $\left(2,0\right)$ -可染的；特别地，当 $n=3$ 时， $C_3^2$ 是 $\left(1,0\right)$ -可染的。

2) 若 $n\ne 0\left(\mathrm{mod}3\right)$ ，则 $C_n^2$ 是 $\left(2,1\right)$ -可染的；特别地，当 $n=4$ 时， $C_4^2$ 是 $\left(2,0\right)$ -可染的。

证明：设 $C_n=v_1{v}_2\cdots v_n{v}_1$ 。考虑 $C_n^2$ 中三个连续的点 $v_{i-1},v_i,v_{i+1}$ ，根据平方图的定义，在 $C_n^2$ 中此三点相互邻接。

1) 若 $n\equiv 0\left(\mathrm{mod}3\right)$ ，不妨假设 $n=3k$ ，则对 $C_{3k}^2$ 进行如下染色c：

当 $i\ne 0\left(\mathrm{mod}3\right)$ 时，令 $c\left(v_i\right)=1$ ；当 $i=0\left(\mathrm{mod}3\right)$ 时，令 $c\left(v_i\right)=2$ 。

当 $k=1$ 时，即 $n=3$ ，显然， $C_3^2$ 是 $\left(1,0\right)$ -可染的(如图2(a))。当 $k\ge 2$ 时，根据平方图的定义，染颜色1的所有点的导出子图是一个圈 $v_1{v}_2{v}_4{v}_5\cdots v_{3j+1}{v}_{3j+2}\cdots v_{3k-2}{v}_{3k-1}$ ，其中 $1\le j\le k-1$ ；染颜色2的点为 $v_3,v_6,\cdots ,v_{3k}$ ，这些点是孤立的(如图2(b)给出了 $C_6^2$ 的染色结果)。因此当 $k\ge 2$ 时， $C_{3k}^2$ 是 $\left(2,0\right)$ -可染的。

2) 若 $n\ne 0\left(\mathrm{mod}3\right)$ ，我们分两种情况讨论。

首先考虑 $n\equiv 1\left(\mathrm{mod}3\right)$ ，不妨假设 $n=3k+1$ ，现对 $C_{3k+1}^2$ 进行如下染色 $c^{\prime }$ ：

当 $k=1$ 时，即 $n=4$ ，令 $c^{\prime }\left(v_1\right)=c^{\prime }\left(v_2\right)=c^{\prime }\left(v_4\right)=1$ ， $c^{\prime }\left(v_3\right)=2$ 。显然 $C_4^2$ 是 $\left(2,0\right)$ -可染的(如图2(c))。当 $k\ge 2$ 时，令 $c^{\prime }\left(v_{3k+1}\right)=c^{\prime }\left(v_{3k}\right)=2$ ；对于 $1\le i\le 3k-1$ ，当 $i\ne 0\left(\mathrm{mod}3\right)$ ，令 $c^{\prime }\left(v_i\right)=1$ ；当 $i=0\left(\mathrm{mod}3\right)$ ，令 $c^{\prime }\left(v_i\right)=2$ 。根据平方图的定义，染颜色1的点导出子图是一条路 $v_1{v}_2{v}_4{v}_5\cdots v_{3j+1}{v}_{3j+2}\cdots v_{3k-2}{v}_{3k-1}$ ，其中 $1\le j\le k-1$ ；而染颜色2的点 $v_3,v_6,\cdots ,v_{3k},v_{3k+1}$ 中，仅有 $v_{3k}$ 和 $v_{3k+1}$ 邻接，其余点均不邻接(如图2(d)给出了 $C_7^2$ 的染色结果，即 $k=3$ )。所以当 $k\ge 2$ 时， $C_{3k+1}^2$ 是 $\left(2,1\right)$ -可染的。

接下来考虑 $n\equiv 2\left(\mathrm{mod}3\right)$ ，不妨假设 $n=3k+2$ ，现对 $C_{3k+2}^2$ 进行染色 $c^{″}$ ：

令 $c^{″}\left(v_{3k+2}\right)=2$ 。对任意的 $v_i$ ， $1\le i\le 3k+1$ ，当 $i\ne 0\left(\mathrm{mod}3\right)$ 时，令 $c^{″}\left(v_i\right)=1$ ；当 $i=0\left(\mathrm{mod}3\right)$ 时，令 $c^{″}\left(v_i\right)=2$ 。根据平方图的定义，染颜色1的点导出子图是一个圈 $v_1{v}_2{v}_4{v}_5\cdots v_{3j+1}{v}_{3j+2}\cdots v_{3k-1}{v}_{3k+1}{v}_1$ ，其中 $1\le j\le k-1$ 。染颜色2的点为 $v_3,v_6,\cdots ,v_{3k},v_{3k+2}$ ，仅 $v_{3k}$ 和 $v_{3k+2}$ 是邻接的，其余点均不邻接(如图2(e)给出了 $C_5^2$ 的染色结果)。所以 $C_{3k+2}^2$ 是 $\left(2,1\right)$ -可染的。

综合以上情况，定理结论成立。

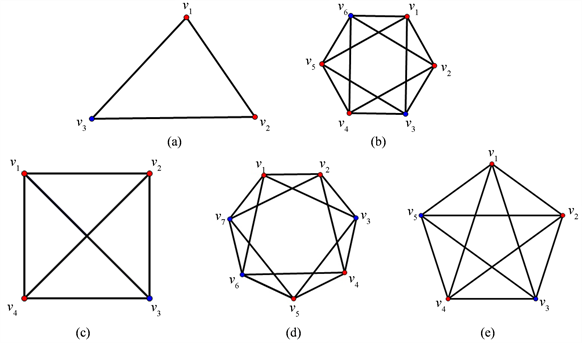(红色表示颜色1，蓝色表示颜色2)

Figure 2. Improper (k, l)-coloring of square graphs of cycles

图2. 圈的平方图的非正常染色