一类耦合KdV型方程的周期波解、孤波解及它们随Hamilton能量的演变关系

Periodic and Solitary Wave Solutions of a Class of Coupled KdV Equation and Their Evolution Relation with Hamilton Energy

摘要: 本文研究了一类非线性耦合KdV型波动方程的精确孤波解、周期波解以及它们随Hamilton能量的演变关系。文中利用平面动力系统的方法对该方程进行了详细的定性分析，通过首次积分法求出了该方程的3种孤波解，其中对有界有理函数波解和扭状孤波解的求解是创新性的解。求出了该方程的7种雅可比椭圆函数周期波解，尤其是利用恰当变换求出了非对称同宿轨所围的闭轨对应的新周期波解，以及包围同宿轨的闭轨对应的新周期波解。文中将所求的孤波解和周期波解与Hamilton能量对应起来，并发现了所研方程为什么能产生孤波解和周期波解，实际上是该方程解的振幅对应的Hamilton系统的能量变化起着关键的作用。

Abstract: In this paper, the exact solitary and periodic wave solutions of a class of nonlinear coupled KdV wave equations and their evolution with Hamilton energy are studied. The equation is qualitative analysis in detail by using the method of planar dynamical system. Three kinds of solitary wave solutions of the equation are obtained by the first integral method, among which the bounded ra-tional function wave solution and the kink-shaped solitary wave solutions are new ones. Seven kinds of Jacobi elliptic function periodic wave solutions of the equation are obtained, especially the new periodic wave solutions corresponding to the closed orbit surrounded by the asymmetric homoclinic orbit and the new periodic wave solutions corresponding to the closed orbit surrounding the homoclinic orbit are obtained by using the appropriate transformation. The soliton and periodic wave solutions are associated with the Hamilton energy, and the reason why the soliton and periodic wave solutions can be produced is found. In fact, the energy change of the Hamilton system corresponding to the amplitude of the solution of the equation plays a key role.

1. 引言

非线性发展方程精确解的研究有重要的理论和实际意义，长期以来，受到国内外应用数学家和物理学家的广泛关注。自Hirota和Satsuma [1] 的工作以来，关于求解耦合非线性发展方程的研究成果已有不少。文献 [2] 求得了耦合方程

$L_6$ (1.1)

型如 $P_i(d_i,0),(i=1,2,3)$ ， $d_i(i=1,2,3)$ 的行波解，Guha-Roy [3] 考虑了如下非线性浅水波耦合方程

$\{\begin{array}{l}{u}_t+\beta {\left(u^3\right)}_x+\alpha {\left({\nu }^3\right)}_x+\lambda {\left(u^2\right)}_x+\gamma u_{xxx}=0,\\ {\nu }_t+\delta {\left(u\nu \right)}_x=0,\end{array}$ (1.2)

并求出了它的椭圆余弦波解

$h=H(d_2,0)$

上式中 $Y=-F_h(x)$ 是 $x$ 的实根。在文献 [4] 中，讨论了如下耦合KdV型方程(为了避免参数过多引起复杂，我们对文献 [4] 中所讨论的方程取定 $e_1=-d_2-\sqrt{-2l-2d_2^2},e_2=e_3=d_2,e_4=-d_2+\sqrt{-2l-2d_2^2}$ ， $d_i(i=1,2,3)$ )

$e_j(j=1,\cdots ,4)$ (1.3)

孤波解的求解，得到了

$e_1<d_1<e_2=e_3=d_2<d_3<e_4$ (1.4)

的孤波解，其中 $h\in (H(d_1,0),H(d_2,0))$ ， $x$ ， $x_i(i=1,\cdots ,4)$ 。文献 [5] 中，作者通过假 $-F_h(x)=-x^4-2l{x}^2-4mx+\frac{12h}{{\mu }_3}=0$ ，其中 $e_1<x_1<x_2<e_2=e_3<x_3<x_4<e_4$ 是魏尔斯特拉斯椭圆函数， $-F_h(x)$ ， $h$ 是任意参数，求出了方程(1.3)如下形式的周期波解

$-F_h(x)=0$ (1.5)

其中 $x_i$ 是 $h$ 的实根。Lu和Yang [6] 求出了该方程的compacton解和peakon解。文献 [7] 中作者还指出了当(1.5)式中模数 $h\to H^{-}(d_2,0)$ ，就可得方程(1.3)的孤波解。文献 [8] 讨论了KdV方程和带时间导数的Boussinesq方程的耦合系统，并探讨了它们的行波解。文献 [9] 研究了一类称为时间分数阶非齐次KdV方程和非线性时间分数阶KdV方程的时间分数阶偏微分方程的数值解。文献 [10] 首次提出了指数函数法求解分数阶非线性系统的两种改进方法，并由此导出了分数阶Hirota-Satsuma耦合KdV系统的一些精确解。显然，当 $x_1\to e_1,x_2\to e_2=d_2,x_3\to e_3=d_2,x_4\to e_4$ 时耦合方程(1.3)就化为组合KdV方程 [11] [12] [13] ，当 $k_3\to 1$ 且 $\underset{h\to H^{-}(d_2,0)}{\lim }{U}_{P4}(\xi )=\underset{k_3\to 1}{\lim }{U}_{P4}(\xi )$ 时(1.3)就化为KdV方程。故方程(1.3)是一个很重要的模型方程。

本文内容具体安排如下：

在第一章中，我们将介绍一类非线性耦合方程的研究状况，然后给出本文的研究内容及创新点。在第二章中，将对方程(1.3)的有界行波解做详细的定性分析，给出其有关孤波解和周期波解的存在条件以及存在个数的若干定理。在第三章中，然后运用首次积分法及适当的变换求出方程(1.3)的3类孤波解(一类解即为 [4] 中的(1.4)式，另外两类是本文得到的新解，其中一个是有界有理解 [14] [15] ，另外一个是扭状孤波解)。在第四章中，我们将对耦合KdV型方程的7类雅可比椭圆函数周期波解求解。在第五章中，我们还将研究该方程周期波解与孤波解随Hamilton能量变化的演化关系。在第六章中，通过各章节的分析与讨论，我们将给出全文的结论。

值得指出：

1) 近来求解非线性发展方程周期波解的精确解及相关问题的研究正受到越来越多学者的关注 [3] [4] [5] [16] - [27] 。但由于计算复杂和技巧性较强的原因，以往文献 [16] [17] [18] 大多只求出了在相图中包含于对称同宿轨的闭轨对应的周期波解，而对于方程所具有的非对称同宿轨线包含的闭轨对应的周期波解的求解以及包围同宿轨的闭轨对应的周期波解的求解，这类问题研究的文献却很少。本文对这一难点开展了研究，通过构造恰当的变换求出了所研方程非对称同宿轨线所围的闭轨对应的周期解及包围同宿轨线的闭轨对应的周期解。这是本文对以往文献的推进之一。

2) 以往求椭圆函数周期波解的文献，很少叙述解中所含模数k究竟是什么 [3] [4] [5] [25] [26] [27] ，以至于使人难以理解它为什么是变量，为什么可以令它趋于1而得到孤波解。本文我们用首次积分方法，并运用恰当的变换不仅求出了孤波解和椭圆函数周期波解，而且对每个求出的椭圆函数周期波解给出了模数k的具体形式，它是Hamilton能量h的函数，h在某相应的区间取值；而每个孤波解则对应于确定的Hamilton能量值。这是有意义的，因为对于一个非线性系统而言，它可能会出现各种各样的复杂现象，我们只有了解和掌握了其中的根本因素，才能去控制或应用这些方程对应的实际系统。文中还给出了所研方程周期波解、孤波解关于Hamilton能量的演变关系。这是本文对以往文献的推进之二。

2. 方程(1.3)行波解的定性分析

设耦合方程(1.3)的行波解为 $=\frac{e_1(e_4-e_2){\mathrm{sech}}^2(\frac{1}{4}\sqrt{\frac{2{\mu }_3}{3}(e_4-e_2)(e_2-e_1)}\xi )+e_4(e_2-e_1)}{(e_4-e_2){\mathrm{sech}}^2(\frac{1}{4}\sqrt{\frac{2{\mu }_3}{3}(e_4-e_2)(e_2-e_1)}\xi )+(e_2-e_1)}$ ， $=d_2-\frac{\sqrt{2}(l+3d_2^2)}{\sqrt{2}{d}_2+\sqrt{-l-d_2^2}\cdot \cosh (\sqrt{-\frac{2{\mu }_3}{3}(l+3d_2^2)}\xi )}=U_{S1}^{+}(\xi )$ ，则 $\underset{h\to H^{-}(d_2,0)}{\lim }{U}_{P3}^{}(\xi )=\underset{k_3\to 1}{\lim }{U}_{P3}^{}(\xi )=U_{S1}^{-}(\xi )$ 和 $h\to H^{-}(d_2,0)$ 满足

$(u_{P3}(\xi ),v_{P3}(\; \xi \; )\; )$

对(2.1)积分一次，得

$(u_{P4}(\xi ),v_{P4}(\; \xi \; )\; )$

其中 $(u_{S1}^{-}(\xi ),v_{S1}^{-}(\xi ))$ ， $(u_{S1}^{+}(\xi ),v_{S1}^{+}(\xi ))$ 为积分常数。由(2.2b)式有

${\mu }_3<0,\Delta <0,m<0$ (2.3)

由于本文求方程(1.3)的有界解，自然要求取 $h=H(d_1,0)$ ，于是有 $Y=F_h(x)$ ， $x$ 满足下列关系

$e_1=e_2=d_1<e_3<e_4$ (2.4)

反之，若 $L_{12}$ 满足关系(2.4)式，则必有 $h\in (H(d_2,0),H(d_1,0))$ 。将(2.4)代入到(2.2)的第一式可得

$U_{P5}^{}\left(\xi \right)$ (2.5a)

其中

$F_h(x)$ (2.5b)

再做平移变换

$x$ (2.6)

则方程(2.5)可化为

$x_i$ (2.7a)

其中

$e_i(i=1,2,3,4)$ (2.7b)

从以上推导可知，若 $x_1<e_1=e_2<x_2<e_3<x_3<e_4<x_4$ 是方程(1.3)的有界行波解，且 $h\to H(d_1,0)$ 满足关系(2.4)式，则经平移变换(2.6)后 $x_1\to e_1,x_2\to e_2,x_3\to e_3,x_4\to e_4$ 满足方程(2.7)。反之，若 $k_4\to 1$ 是方程(2.7)具三阶连续导数的解，取 $\underset{h\to H(d_1,0)}{\lim }{U}_{P5}(\xi )=\underset{k_4\to 1}{\lim }{U}_{P5}(\xi )$ 满足(2.6)式， $=\frac{e_3(e_4-e_2)-e_4(e_3-e_2){\text{sech}}^2(\frac{1}{4}\sqrt{-\frac{2{\mu }_3}{3}(e_4-e_2)(e_3-e_1)}\xi )}{(e_4-e_2)-(e_3-e_2){\text{sech}}^2(\frac{1}{4}\sqrt{-\frac{2{\mu }_3}{3}(e_4-e_2)(e_3-e_1)}\xi )}$ 如(2.4)式，则 $=d_1-\frac{\sqrt{2}(l+3d_1^2)}{\sqrt{2}{d}_1-\sqrt{-l-d_1^2}\cdot \text{cosh}(\sqrt{-\frac{2{\mu }_3}{3}(l+3d_1^2)}\xi )}=U_{S3}^{}(\xi )$ 必满足(2.1)，从而是方程(1.3)的有界行波解。因此，为研究方程(1.3)满足关系式(2.4)的孤波解以及周期波解，我们可以从方程(2.7)出发。

现在我们对方程(2.7)进行定性分析。令 $h\to H(d_1,0)$ 和 $(u_{P5}(\xi ),v_{P5}(\xi ))$ ，则方程(2.7)化为如下的平面动力系统

$(u_{S3}(\xi ),v_{S3}(\xi ))$ (2.8)

在 ${\mu }_3>0,\Delta <0,m<0$ 平面上，系统(2.8)的有限远奇点的个数依赖于方程

$h=H(d_2,0)$ (2.9)

的实根的个数。记

$L_5$ (2.10)

为方程 $L_6$ 的判别式。易知 $(u_{S1}^{\pm }(\xi ),v_{S1}^{\pm }(\xi ))$ 时，方程 $h>H(d_2,0)$ 有一实根和两复根；在 $L_5$ ， $L_6$ 时，方程 $(u_{P7}^{+}(\xi ),v_{P7}^{+}(\xi ))$ 有1个单实根和1个二重实根；在 ${\beta }^2\text{+}(\alpha -{\gamma }_1)(\alpha -{\gamma }_{\text{2}})<0$ 时， ${(\frac{{\gamma }_1+{\gamma }_2}{2})}^2<\frac{-l}{3}$ 有3个互异实根。由于 $k_5^2>\frac{1}{2}$ 仅有一实根时，方程(2.7)无有界解，从而方程(1.3)无有界行波解，而本文着重于方程(1.3)有界解的讨论，故本文以下始终假定 $x$ 且 ${\gamma }_1,{\gamma }_2$ 。此时若设 ${\gamma }_2<d_1=\frac{-d-\sqrt{-3d^2-4l}}{2}<d_2=d<d_3=\frac{-d+\sqrt{-3d^2-4l}}{2}<{\gamma }_1$ 是方程 $h\to H^{+}(d_2,0)$ 的3个实根，系统(2.8)就有3个有限远奇点 ${\gamma }_2\to -d_2-\sqrt{-2l-2d_2^2},{\gamma }_1\to -d_2+\sqrt{-2l-2d_2^2},$ ；不妨假设 $\alpha =-\frac{1}{2}({\gamma }_1+{\gamma }_2)\to d_2,\beta \to 0$ ，则由多项式根与系数的关系知

$\rho \to \frac{-l-3d^2}{2d^2},{\lambda }_1\to 0,{\lambda }_2\to -\frac{l+3d^2}{l+d^2},k_5\to 1$ (2.11)

记系统(2.8)在 $\underset{h\to H^{+}(d_2,0)}{\lim }{U}_{P7}^{+}\left(\xi \right)=\underset{k5\to 1}{\lim }{U}_{P7}^{+}\left(\xi \right)$ 处的Jacobi矩阵为

$=\underset{k5\to 1}{\lim }\frac{1-{\lambda }_1}{1\text{+}{\lambda }_1}\alpha -\frac{2\alpha \rho }{1+\sqrt{\frac{1+{\lambda }_1}{1+{\lambda }_2}}\cdot \text{cn}(\alpha \sqrt{\frac{2{\mu }_3\rho }{3}}\xi ,k_5)}$

由平面动力系统的知识 [28] [29] 可知，系统(2.8)是Hamilton系统，有首次积分

$=d_2-\frac{\sqrt{2}(l+3d_2{}^2)}{\sqrt{2}{d}_2\pm \sqrt{-l-d_2{}^2}\cdot \cosh (\sqrt{-\frac{{\mu }_3}{3}(l+3d_2{}^2)}\xi )}=U_{S1}^{\pm }(\xi )$ (2.12)

易知(2.12)式也是系统(2.8)的Hamilton能量函数。

利用平面动力系统的理论和方法 [28] [29] ，我们对系统(2.8)从如下两个方面进行定性分析。

2.1. 系统(2.8)的有限远奇点类型

1) 在 $h\to H^{+}(d_2,0)$ 情形

① $(u_{P7}^{+}(\xi ),v_{P7}^{+}(\xi ))$ 时

a) 当 $(u_{S1}^{\pm }(\xi ),v_{S1}^{\pm }(\xi ))$ 时，方程 ${\mu }_3>0,l<0,m<0,\Delta <0$ 存在3个不同的实根 $h=H(d_2,0)$ 和 $(u_{S1}^{\pm }(\xi ),v_{S1}^{\pm }(\xi ))$ ，且 $H(d_1,0)<h<H(d_2,0)$ ，对应系统(2.8)有3个不同的有限远奇点 $(u_{P3}(\xi ),v_{P3}(\xi ))$ 。雅可比矩阵 $(u_{P4}(\xi ),v_{P4}(\xi ))$ 的行列式分别为

$h\to H(d_2,0)$

$(u_{P3}(\xi ),v_{P3}(\xi ))\to (u_{S1}^{-}(\xi ),v_{S1}^{-}(\; \xi \; )\; )$

$(u_{P4}(\xi ),v_{P4}(\xi ))\to (u_{S1}^{+}(\xi ),v_{S1}^{+}(\; \xi \; )\; )$

故 $v(\xi )与u(\xi )$ 和 $h\to H(d_2,0)$ 为中心， $u_{P4}(\xi )$ 为鞍点。

b) 当 $u_{S1}^{\text{+}}(\xi )$ 时，方程 ${\mu }_3=4$ 存在两个不同的实根 $l=-3,m=-1,c=1,\epsilon =2$ 和 $d_2\text{=}-\text{0}\text{.3472963553}$ ，且 $H(d_2,0)=\text{0}\text{.2266815969}$ ， $h\to H^{-}(d_2,0)$ 和 $u_{P4}(\xi )$ 重合，即点 $u_{S1}^{\text{+}}(\xi )$ 与 $h=\text{0}\text{.21668}$ 重合，记为 $u_{P4}(\xi )$ 。对应系统(2.8)有2个不同的有限远奇点 $h=0.22668$ 和 $u_{P4}(\xi )$ ，由(2.11)知

$h=\text{0}\text{.21668}$

雅可比矩阵 $u_{P4}(\xi )$ 的行列式分别为

$h=0.22668$

$u_{P4}(\; \xi \; )$

故 $h=\text{0}\text{.2266815}$ 为中心， $u_{P4}(\xi )$ 为尖点。

② $h=H(d_2,0)$ 时

a) 当 $u_{S1}^{+}(\xi )$ 时，方程 $h=\text{0}\text{.2266815}$ 存在3个不同的实根 $u_{P4}(\xi )$ 和 $h=H(d_2,0)$ ，且 $u_{S1}^{+}(\xi )$ ，对应系统(2.8)有3个不同的有限远奇点 ${\mu }_3<0,l<0,m=0,\Delta <0$ 。雅可比矩阵 $h\text{=}H(d_1,0)=H(\sqrt{-l},0)=-\frac{{\mu }_3{l}^2}{12}$ 的行列式分别为

$(u_{S5}^{\pm }(\xi ),v_{S5}^{\pm }(\; \xi \; )\; )$

$C_1=0$

$u\text{'}\text{'}+\frac{1}{3}{\mu }_3{u}^3+\frac{1}{2}{\mu }_2{u}^2-{\mu }_{1}u=C_2,$

故 ${\mu }_1=\frac{8\alpha c^2\delta +c{\epsilon }^3}{\gamma {\epsilon }^3},{\mu }_2=\frac{16\alpha c+\lambda {\epsilon }^3}{{\epsilon }^3},{\mu }_3=\frac{\beta {\epsilon }^3-8\alpha }{{\epsilon }^3},C_2=\frac{3C_0{\epsilon }^3-8\alpha c^3}{3{\epsilon }^3}.$ 和 $U(\xi )=u(\xi )+\frac{{\mu }_2}{2{\mu }_3}$ 为中心， $U^{″}(\xi )+\frac{{\mu }_3}{3}(U^3(\xi )+lU(\xi )+m)=0$ 为鞍点。

b) 当 $l=-\frac{12{\mu }_1{\mu }_3+3{\mu }_2^2}{4{\mu }_3^2},m=\frac{{\mu }_2^3+6{\mu }_1{\mu }_2{\mu }_3-12{\mu }_3^2{C}_2}{4{\mu }_3^3}.$ 时，方程 $(u(\xi ),v(\xi ))$ 存在两个不同的实根 $u(\xi ),v(\xi )$ 和 $U(\xi )$ ，且 $U(\xi )$ ， $u(\xi )$ 和 $v(\xi )$ 重合，即点 $(u(\xi ),v(\xi ))$ 与 $x=U(\xi )$ 重合，对应系统(2.8)有2个不同的有限远奇点 $y=U^{\prime }(\xi )$ 和 $\{\begin{array}{l}\frac{dx}{d\xi }=y\triangleq P(x,y)，\\ \frac{dy}{d\xi }=-\frac{{\mu }_3}{3}(x^3+lx+m)\triangleq Q(x,y).\end{array}$ 。由(2.11)知

$(x,y)$

雅可比矩阵 $\phi (x)\triangleq x^3+lx+m=0$ 的行列式分别为

$\Delta =27m^2+4l^3$

$\phi (x)=0$

故 $\Delta >0$ 为尖点， $\phi (x)=0$ 为中心。

③ $l<0,\Delta =0$ 时

此时 $\phi (x)=0$ ，方程 $\Delta <0$ 存在3个不同的实根 $\phi (x)=0$ 和 $\phi (x)=0$ ，对应系统(2.8)有3个不同的有限远奇点 $l<0$ 。它们的雅可比矩阵 $\Delta \le 0$ 的行列式分别为

$d_i$

$(i=1,2,3)$

故 $\phi (x)=0$ 和 $P_i(d_i,0)$ 为中心， $(i=1,2,3)$ 为鞍点。

2) 在 $d_1\le d_2\le d_3$ 情况下

① $\{\begin{array}{l}{d}_1+d_2+d_3=0,\\ d_1{d}_2+d_1{d}_3+d_2{d}_3=l,\\ d_1{d}_2{d}_3=-m.\end{array}$ 时

a) 当 $P_i$ 时，方程 $(i=1,2,3)$ 存在3个不同的实根 $J(d_i,0)=\left(\begin{array}{cc}0& 1\\ -\frac{{\mu }_3{\phi }^{\prime }(d_i)}{3}& 0\end{array}\right)$ 和 $i=1,2,3$ ，且 $H(x,y)\text{=}\frac{1}{2}{y}^2+\frac{{\mu }_3}{12}(x^4+2l{x}^2+4mx)=h$ ，对应系统(2.8)有3个不同的有限远奇点 $h\in R$ 。雅可比矩阵 ${\mu }_3>0$ 的行列式分别为

$m>0$

$\Delta <0$

$\phi (x)=0$

故 $d_1,d_2$ 和 $d_3$ 为鞍点， $d_1<-d_3<-d_2<0<d_2<d_3$ 为中心。

b) 当 $P_i(d_i,0)$ 时，方程 $(i=1,2,3)$ 存在两个不同的实根 $J(d_i,0)(i=1,2,3)$ 和 $\det J(d_1,0)=\frac{{\mu }_3}{3}(3d_1^2+l)>\frac{{\mu }_3}{3}(3d_3^2+l)=\det J(d_3,0),$ ，且 $\det J(d_2,0)=\frac{{\mu }_3}{3}(3d_2^2+l)=\frac{{\mu }_3}{3}(2d_2^2+d_1{d}_3)<\frac{{\mu }_3}{3}(2d_2^2+d_1{d}_2)<\frac{{\mu }_3}{3}(d_2^2+d_1{d}_2+d_2{d}_3)=0,$ ， $\det J(d_3,0)=\frac{{\mu }_3}{3}(3d_3^2+l)=\frac{{\mu }_3}{3}(2d_3^2+d_1{d}_2)>\frac{{\mu }_3}{3}(2d_3^2+d_1{d}_3)>\frac{{\mu }_3}{3}(d_3^2+d_1{d}_3+d_2{d}_3)=0,$ 和 $P_1$ 重合，即点 $P_3$ 与 $P_2$ 重合，记为 $\Delta =0$ 。对应系统(2.8)有2个不同的有限远奇点 $\phi (x)=0$ 和 $d_1$ ，由(2.11)知

$d_3$

雅可比矩阵 $d_1<0<d_3$ 的行列式分别为

$d_2$

$d_3$

故 $P_2(d_2,0)$ 为鞍点， $P_3(d_3,0)$ 为尖点。

② $P_{2,3}(d_{2,3},0)$ 时

a) 当 $P_1(d_1,0)$ 时，方程 $P_{2,3}(d_{2,3},0)$ 存在3个不同的实根 $\{\begin{array}{l}{d}_1+2d_3=0,\\ 2d_1{d}_3+d_3^2=l,\\ d_1{d}_3^2=-m.\end{array}$ 和 $J(d_i,0)(i=1,2,3)$ ，且 $\det J(d_1,0)=\frac{{\mu }_3}{3}(3d_1^2+l)=\frac{{\mu }_3}{3}(3d_1^2+d_3^2+2d_1{d}_3)=\frac{{\mu }_3}{3}{d}_3^2>0,$ ，对应系统(2.8)有3个不同的有限远奇点 $\det J(d_{2,3},0)=\frac{{\mu }_3}{3}(3d_{2,3}^2+l)=\frac{{\mu }_3}{3}(4d_{2,3}^2+2d_1{d}_{2,3})=0.$ 。雅可比矩阵 $P_1$ 的行列式分别为

$P_{2,3}$

$m<0$

$\Delta <0$

故 $\phi (x)=0$ 和 $d_1,d_2$ 为鞍点， $d_3$ 为中心。

b) 当 $d_1<d_2<0<-d_2<-d_1<d_3$ 时，方程 $P_i(d_i,0)$ 存在两个不同的实根 $(i=1,2,3)$ 和 $J(d_i,0)(i=1,2,3)$ ，且 $\det J(d_1,0)=\frac{{\mu }_3}{3}(3d_1^2+l)=\frac{{\mu }_3}{3}(2d_1^2+d_2{d}_3)>\frac{{\mu }_3}{3}(2d_1^2+d_1{d}_3)>\frac{{\mu }_3}{3}(d_1^2+d_1{d}_2+d_1{d}_3)=0,$ ， $\det J(d_2,0)=\frac{{\mu }_3}{3}(3d_2^2+l)=\frac{{\mu }_3}{3}(2d_2^2+d_1{d}_3)<\frac{{\mu }_3}{3}(2d_2^2+d_2{d}_3)<\frac{{\mu }_3}{3}(d_2^2+d_1{d}_2+d_2{d}_3)=0,$ 和 $\det J(d_3,0)=\frac{{\mu }_3}{3}(3d_3^2+l)>\frac{{\mu }_3}{3}(3d_1^2+l)=\det J(d_1,0)>0.$ 重合，即点 $P_1$ 与 $P_3$ 重合，对应系统(2.8)有2个不同的有限远奇点 $P_2$ 和 $\Delta =0$ 。由(2.11)知

$\phi (x)=0$

雅可比矩阵 $d_1$ 的行列式分别为

$d_3$

$d_1<0<d_3$

故 $d_2$ 为尖点， $d_1$ 为鞍点。

③ $P_2(d_2,0)$ 时

此时 $P_1(d_1,0)$ ，方程 $P_{1,2}(d_{1,2},0)$ 存在3个不同的实根 $P_3(d_3,0)$ 和 $\{\begin{array}{l}2d_1+d_3=0,\\ d_1^2+2d_1{d}_3=l,\\ d_1^2{d}_3=-m.\end{array}$ 。对应系统(2.8)有3个不同的有限远奇点 $J(d_i,0)(i=1,2,3)$ ，雅可比矩阵 $\det J(d_{1,2},0)=\frac{{\mu }_3}{3}(3d_{1,2}^2+l)=\frac{{\mu }_3}{3}(4d_{1,2}^2+2d_1{d}_3)=0,$ 的行列式分别为

$\det J(d_3,0)=\frac{{\mu }_3}{3}(3d_3^2+l)>0.$

$P_{1,2}$

故 $P_3$ 和 $m=0$ 为鞍点， $\Delta <0$ 为中心。

2.2. 系统(2.8)的全局相图以及方程(1.3)有界行波解的存在性

综合以上的定性分析，我们可以得到系统(2.8)在不同的参数条件下的全局相图

1) 在 $\phi (x)=0$ 的情况下

Figure 1. m = 0, Δ < 0

图1. m = 0, Δ < 0

Figure 2. m > 0, Δ < 0

图2. m > 0, Δ < 0

Figure 3. m < 0, Δ < 0

图3. m < 0, Δ < 0

Figure 4. m > 0, Δ = 0

图4. m > 0, Δ = 0

Figure 5. m < 0, Δ = 0

图5. m < 0, Δ = 0

2) 在 $-d_1=d_3=\sqrt{-l}$ 的情况下

Figure 6. m = 0, Δ < 0

图6. m = 0, Δ < 0

Figure 7. m > 0, Δ < 0

图7. m > 0, Δ < 0

Figure 8. m < 0, Δ < 0

图8. m < 0, Δ < 0

Figure 9. m > 0, Δ = 0

图9. m > 0, Δ = 0

Figure 10. m < 0, Δ = 0

图10. m < 0, Δ = 0

进一步，根据全局相图图1~10，我们可得如下性质和定理。

性质2.1设 $d_2=0$ ， $P_i(d_i,0)$ 。

1) 当 $(i=1,2,3)$ 时，系统(2.8)在 $J(d_i,0)(i=1,2,3)$ ， $\det J(d_{1,3},0)=\frac{{\mu }_3}{3}(3d^2{}_{1,3}+l)=-\frac{2{\mu }_{3}l}{3}>0,$ 和 $\det J(d_2,0)=\frac{{\mu }_3}{3}(3d_{{}_2}^2+l)=\frac{{\mu }_{3}l}{3}<0.$ 条件下分别存在两条同宿轨和无穷多条闭轨(见图1~3)。

2) 当 $P_1$ 时，系统(2.8)在 $P_3$ 和 $P_2$ 条件下分别存在一条同宿轨和无穷多条闭轨(见图4，图5)。

性质2.2设 ${\mu }_3<0$ ， $m>0$ 。

1) 当 $\Delta <0$ 时，系统(2.8)在 $\phi (x)=0$ 和 $d_1,d_2$ 条件下分别存在一条同宿轨和无穷多条闭轨(见图7，图8)，在 $d_3$ 条件下存在两条异宿轨和无穷多条闭轨(见图6)。

2) 当 $d_1<-d_3<-d_2<0<d_2<d_3$ 时，系统(2.8)在 $P_i(d_i,0)$ 和 $(i=1,2,3)$ 条件下均不存在有界轨线(见图9，图10)。

根据性质2.1，性质2.2以及有界轨线和行波解的对应关系：同宿轨、异宿轨、闭轨分别对应方程(2.7)的钟状解、扭状解、周期解，从而分别对应方程(1.3)的钟状孤波解、扭状孤波解、周期波解；我们可得耦合方程(1.3)周期波解和孤波解的如下两个定理。

定理2.1设 $J(d_i,0)(i=1,2,3)$ ， $\det J(d_1,0)=\frac{{\mu }_3}{3}(3d_1^2+l)<\frac{{\mu }_3}{3}(3d_3^2+l)=\det J(d_3,0),$ 。

1) 当 $\det J(d_2,0)=\frac{{\mu }_3}{3}(3d_2^2+l)=\frac{{\mu }_3}{3}(2d_2^2+d_1{d}_3)>\frac{{\mu }_3}{3}(2d_2^2+d_1{d}_2)>\frac{{\mu }_3}{3}(d_2^2+d_1{d}_2+d_2{d}_3)=0,$ 时，方程(1.3)在 $\det J(d_3,0)=\frac{{\mu }_3}{3}(3d_3^2+l)=\frac{{\mu }_3}{3}(2d_3^2+d_1{d}_2)<\frac{{\mu }_3}{3}(2d_3^2+d_1{d}_3)<\frac{{\mu }_3}{3}(d_3^2+d_1{d}_3+d_2{d}_3)=0.$ ， $P_1$ 和 $P_3$ 条件下分别存在两个钟状孤波解和无穷多个周期波解。

2) 当 $P_2$ 时，方程(1.3)在 $\Delta =0$ 和 $\phi (x)=0$ 条件下分别存在一个钟状孤波解和无穷多个周期波解。

定理2.2设 $d_1$ ， $d_3$ 。

1) 当 $d_1<0<d_3$ 时，方程(1.3)在 $d_2$ 和 $d_3$ 条件下分别存在一个同宿轨和无穷多个周期波解，在 $P_2(d_2,0)$ 情况下存在两个扭状孤波解和无穷个周期波解。

2) 当 $P_3(d_3,0)$ 时，方程(1.3)在 $P_{2,3}(d_{2,3},0)$ 和 $P_1(d_1,0)$ 条件下均不存在有界行波解。

3. 方程(1.3)的孤波求解

据第二节知道，求方程(1.3)满足关系(2.4)的有界解可转化为方程(2.7)。方程(2.7)对应于平面动力系统(2.8)，其首次积分为(2.12)式。据平面动力系统知识 [28] [29] 可知，这首次积分式(2.12)是方程(2.7)的解所对应的轨线的一般表达式。因此，我们可利用这首次积分式(2.12)求得方程(2.7)的钟状解、扭状解和周期解，进而得到方程(1.3)的孤波解和周期波解。

又由于平面动力系统(2.8)是Hamilton系统，同一闭轨线上点的Hamilton能量h是相等的。故在给定参数条件下，对于 $P_{2,3}(d_{2,3},0)$ 全局相图中具有能量h的闭轨线 $\{\begin{array}{l}{d}_1+2d_3=0,\\ 2d_1{d}_3+d_3^2=l,\\ d_1{d}_3^2=-m.\end{array}$ 是唯一确定的。本节将求的钟状孤波解即为图1~3中具能量 $J(d_i,0)(i=1,2,3)$ 同宿轨对应的解，图7中具能量 $\det (J(d_1,0))=\frac{{\mu }_3}{3}(3d_1^2+l)=\frac{{\mu }_3}{3}(3d_1^2+d_3^2+2d_1{d}_3)=\frac{{\mu }_3}{3}{d}_3^2<0,$ 的同宿轨和图8中具能量 $\det (J(d_{2,3},0))=\frac{{\mu }_3}{3}(3d_{2,3}^2+l)=\frac{{\mu }_3}{3}(4d_{2,3}^2+2d_1{d}_{2,3})=0.$ 的同宿轨对应的解；还有图4具能量 $P_1$ 的同宿轨和图5具能量 $P_{2,3}$ 的同宿轨对应的解，本节将求的扭状解即为图6中具能量 $m<0$ 的两对称异宿轨(这俩异宿轨形成闭轨)对应的解。

由系统(2.8)的首次积分(2.12)，得

$\Delta <0$ (3.1)

其中 $\phi (x)=0$ 表示系统(2.8)在 $d_1,d_2$ 点处的Hamilton能量。

由于 $d_3$ ，通过分离变量法，求方程(2.7)有界解的问题可转化为下列积分

$d_1<d_2<0<-d_2<-d_1<d_3$ (3.2a)

其中

$P_i(d_i,0)$ (3.2b)

且当 $(i=1,2,3)$ 时(3.2a)式根号内函数取 $J(d_i,0)(i=1,2,3)$，当 $\det J(d_1,0)=\frac{{\mu }_3}{3}(3d_1^2+l)=\frac{{\mu }_3}{3}(2d_1^2+d_2{d}_3)<\frac{{\mu }_3}{3}(2d_1^2+d_1{d}_3)<\frac{{\mu }_3}{3}(d_1^2+d_1{d}_2+d_1{d}_3)=0,$ 时(3.2a)式根号内函数取 $\det J(d_2,0)=\frac{{\mu }_3}{3}(3d_2^2+l)=\frac{{\mu }_3}{3}(2d_2^2+d_1{d}_3)>\frac{{\mu }_3}{3}(2d_2^2+d_2{d}_3)>\frac{{\mu }_3}{3}(d_2^2+d_1{d}_2+d_2{d}_3)=0,$ 。

3.1. 图1~3对应的钟状孤波解

图1~3中能量 $\det J(d_3,0)=\frac{{\mu }_3}{3}(3d_3^2+l)<\frac{{\mu }_3}{3}(3d_1^2+l)=\det J(d_1,0)<0.$ 的同宿轨对应的 $P_1$ 在x轴有4个零点，其中 $P_3$ 为 $P_2$ 的二重根。由于 $\Delta =0$ ，又 $\phi (x)=0$ 同时为(2.9)式 $d_1$ 的实根，有 $d_3$ ，故有

$d_1<0<d_3$ (3.3)

其中 $d_2$ 为当 $d_1$ 时 $P_2(d_2,0)$ 与x轴的两交点，

$P_1(d_1,0)$ (3.4)

将(3.3)式代入(3.2)，则积分式可化为

$P_{1,2}(d_{1,2},0)$ (3.5)

此时有 $P_3(d_3,0)$ ，当 $\{\begin{array}{l}2d_1+d_3=0,\\ d_1^2+2d_1{d}_3=l,\\ d_1^2{d}_3=-m.\end{array}$ 时，令 $J(d_i,0)(i=1,2,3)$ ，我们可得

$\det J(d_{1,2},0)=\frac{{\mu }_3}{3}(3d_{1,2}^2+l)=\frac{{\mu }_3}{3}(4d_{1,2}^2+2d_1{d}_3)=0,$ (3.6)

于是，当 $\det J(d_3,0)=\frac{{\mu }_3}{3}(3d_3^2+l)<0.$ 时，有

$P_{1,2}$ (3.7a)

而当 $P_3$ 时，有

$m=0$ (3.7b)

其中(3.7)中 $\Delta <0$ ，据(3.7a) (3.7b)分别解出x，并化简得

$\phi (x)=0$ (3.8)

上式中 $-d_1=d_3=\sqrt{-l}$ 时，(3.8)式分母中取“−”号，当 $d_2=0$ 时(3.8)式分母中取“+”号，将(3.4)代入上式，化简得

$P_i(d_i,0)$ (3.9)

综上，我们可得如下定理。

定理3.1：设 $(i=1,2,3)$ ， $J(d_i,0)(i=1,2,3)$ ， $\det J(d_{1,3},0)=\frac{{\mu }_3}{3}(3d_{1,3}+l)=-\frac{2{\mu }_{3}l}{3}<0,$ ， $\det J(d_2,0)=\frac{{\mu }_3}{3}(3d_2^2+l)=\frac{{\mu }_{3}l}{3}>0.$ ，当Hamilton能量 $P_1$ 时，方程(1.3)有钟状孤波解

$P_3$ (3.10)

(3.10)式中 $P_2$ 由(3.9)式给定，对应于全局相图图2，图3中同宿轨。

由于，当 ${\mu }_3>0$ 时，有 $m=0,\Delta <0$ ，此时(3.9)式可化为

$m>0,\Delta <0$ (3.11)

故我们有如下推论。

推论1. 设 $m<0,\Delta <0$ ， $m=0,\Delta <0$ ， $m>0,\Delta <0$ ， $m<0,\Delta <0$ ，当Hamilton能量 $m>0,\Delta =0$ 时，方程(1.3)有钟状孤波解

$m<0,\Delta =0$ (3.12)

(3.12)式中 $m>0,\Delta =0$ 由(3.11)给出，对应于相图1中同宿轨线。

3.2. 图7、图8同宿轨线对应的孤波解

先考虑图7中同宿轨对应的钟状孤波解的求解。此时 $m<0,\Delta =0$ ， ${\mu }_3<0$ ，由于此时同宿轨对应的Hamilton能量 $m=0,\Delta <0$ ，又d₃是 $m<0,\Delta <0$ 的二重根，同时也为方程(2.9)的根，有 $m=0,\Delta <0$ ，故此时 $m>0,\Delta <0$ 可表达为

$m<0,\Delta <0$ (3.13)

其中 $m>0,\Delta =0$ 为此时 $m<0,\Delta =0$ 与x轴的交点

$m>0,\Delta =0$ (3.14)

且 $m<0,\Delta =0$ 。将(3.13)式代入(3.2)，并在 ${\mu }_3>0,l<0$ 上做类似于3.1段的积分和化简，可得图7同宿轨对应的钟状解为

$\Delta <0$ (3.15)

再考虑相图8同宿轨对应的钟状解。此时 $m>0,m=0$ ，同宿轨对应Hamilton能量值为 $m<0$ 。此时有

$\Delta =0$ (3.16)

其中 $m>0$ 为 $m<0$ 与x轴交点的横坐标，

${\mu }_3<0,l<0$ (3.17)

且 $\Delta <0$ 。将(3.16)式代入(3.2a)，并在 $m>0$ 上做类似于3.1段的积分和化简，可得图8同宿轨对应的钟状解为

$m<0$ (3.18)

综上，我们可得如下定理。

定理3.2：设 $m=0$ ， $\Delta =0$ ， $m>0$ 。

1) 当 $m<0$ ，Hamilton能量为 ${\mu }_3>0,l<0$ 时，方程(1.3)有钟状孤波解

$\Delta <0$ (3.19)

其中 $m>0,m=0$ 由(3.15)式给定，对应图7中同宿轨。

2) 当 $m<0$ ，Hamilton能量为 $\Delta =0$ 时，方程(1.3)有钟状孤波解

$m>0$ (3.20)

其中 $m<0$ 由(3.18)式给定，对应图8中同宿轨。

3.3. 图4、图5同宿轨线对应的孤波解

先考虑图4同宿轨对应的钟状解。

此时 ${\mu }_3<0,l<0$ ， $\Delta <0$ ， $m>0$ ， $m<0$ 是 $m=0$ 的二重根。根据多项式根与系数的关系有 $\Delta =0$ ， $m>0$ ， $m<0$ 。可推得 $h$ ，且

$\forall h\in R$

又由 $h$ 即 $G_h=\{(x,y)\in R\times R\text{|}H(x,y)=h\}$ ，本段由于 $H(d_2,0)$ ，取 $H(d_3,0)$ ，故有

$H(d_1,0)$ (3.21)

将上式代入(3.2a)，并注意到此时 $H(d_3,0)$ ，可得

$H(d_1,0)$ (3.22)

上式解出x，即可得

$H(d_1,0)$ (3.23)

类似地，可求得图5同宿轨线对应的钟状解。

在图5情形，此时 $y^2=-\frac{{\mu }_3}{6}(x^4+2l{x}^2+4mx)+2h=-\frac{{\mu }_3}{6}(x^4+2l{x}^2+4mx-\frac{12h}{{\mu }_3})$ ， $h=H(x,y)$ ， $(x,y)$ ， $y=x\text{'}$ 是 ${\displaystyle \int \frac{dx}{\sqrt{\pm F_h(x)}}}=\pm \sqrt{\frac{\left|{\mu }_3\right|}{6}}(\xi -{\xi }_0),$ 的二重根。根据多项式根与系数的关系有 $F_h(x)=x^4+2l{x}^2+4mx-\frac{12h}{{\mu }_3}$ ， ${\mu }_3>0$ ， $-F_h(x)$ 。可推得 ${\mu }_3<0$ ，且

$F_h(\; x\; )$

又由 $H(d_2,0)$ 即 $F_h(x)$ ，可得 $x$ ，

$d_2$ (3.24)

将上式代入(3.2)，并注意到 $F_h(x)=0$ ，可得(作变换 $H(d_2,0)=\frac{{\mu }_3}{12}(d_2^4+2l{d}_2^2+4m{d}_2)$ )

$d_2$ (3.25)

上式解出x，即可得

$\phi (x)=0$ (3.26)

综上可得如下定理。

定理3.3：设 ${\mu }_3>0$ ， $l<0$ ， $\Delta =0$ 。

1) 当 $-F_h(x)=-{(x-d_2)}^2(x^2+2d_{2}x+3d_2^2+2l)=-{(x-d_2)}^2(x-r_1)(x-r_2),$ ，Hamilton能量为 $r_1,r_2$ 时，方程(1.3)有孤波解

$h=H(d_2,0)$ (3.27)

(3.27)式中 $F_h(x)=0$ 由(3.23)式给出，对应相图4中同宿轨。

2) 当 $x$ ，Hamilton能量为 $r_1=-d_2-\sqrt{-2l-2d_2^2},r_2=-d_2+\sqrt{-2l-2d_2^2}.$ 时，方程(1.3)有孤波解

$\pm \sqrt{\frac{{\mu }_3}{6}}(\xi -{\xi }_0)={\displaystyle \int \frac{dx}{\sqrt{-{(x-d_2)}^2(x-r_1)(x-r_2)}}}$ (3.28)

(3.28)式中 $={\displaystyle \int \sqrt{\frac{r_2-x}{x-r_1}}\frac{dx}{(x-d_2)(r_2-x)}}.$ 由(3.26)式给出，对应相图5中同宿轨。

3.4. 图6对称异宿轨线对应的扭状孤波解

此时 $r_1<d_2<r_2$ ， $x\in (r_1,d_2)\cup (d_2,r_2)$ ，由于 $t=\sqrt{\frac{r_2-x}{x-r_1}}$ 为 $\pm \sqrt{\frac{{\mu }_3}{6}}(\xi -{\xi }_0)=-\frac{1}{\sqrt{(d_2-r_1)(r_2-d_2)}}\left[\ln \left|t+\sqrt{\frac{r_2-d_2}{d_2-r_1}}\right|-\ln \left|t-\sqrt{\frac{r_2-d_2}{d_2-r_1}}\right|\right].$ 的根，有 $x\in (r_1,d_2)$ ，

$t=-\sqrt{\frac{r_2-d_2}{d_2-r_1}}\cdot \frac{e^{\Omega }+1}{e^{\Omega }-1},$ ，此时有

$x\in (d_2,r_2)$ (3.29)

把(3.29)代入(3.2)式，有

$t=-\sqrt{\frac{r_2-d_2}{d_2-r_1}}\cdot \frac{e^{\Omega }-1}{e^{\Omega }+1}.$ (3.30)

由于此时 $\Omega =\pm \sqrt{\frac{{\mu }_3}{6}(d_2-r_1)(r_2-d_2)}(\xi -{\xi }_0)$ ，(3.30)可以化为

$x$ (3.31)

上式进一步关于x解出，可得图6异宿轨对应的扭状解

$x(\xi )=d_2-\frac{2(d_2-r_2)(d_2-r_1)}{4d_2\pm (r_2-r_1)\cosh \sqrt{\frac{{\mu }_3}{6}(d_2-r_1)(r_2-d_2)}(\xi -{\xi }_0)}.$ (3.32)

由此，我们可得如下定理。

定理3.4：设 $x\in (r_1,d_2)$ ， $-$ ， $x\in (d_2,r_2)$ ， $+$ ，则方程(2.7)有扭状孤波解

$U_{S1}^{\pm }(\xi )=d_2-\frac{2(l+3d_2^2)}{2d_2\pm \sqrt{-2l-2d_2^2}\cosh \sqrt{\frac{-{\mu }_3}{3}(l+3d_2^2)}(\xi -{\xi }_0)}.$

从而方程(1.3)有扭状孤波解

$l<0,{\mu }_3>0,\Delta <0,m\ne 0$ (3.33)

值得指出，文献 [11] 中，曾求出方程(1.3)的钟状孤波解(1.4)式，即文献 [6] 中的(9)式，其特点是孤波解的渐近值为零。由本文定理3.1中(3.9) (3.10)知，这相当于是 $h=H(d_2,0)$ 时的孤波解 $\{\begin{array}{l}{u}_{S1}^{\pm }(x,t)=U_{S1}^{\pm }(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{S1}^{\pm }(x,t)=\frac{2}{\epsilon }\left(c-u_{S1}^{\pm }(\xi )\right).\end{array}$ 。因为当 $U_{S1}^{\pm }(\xi )$ 为方程 $m=0$ 的根时，由于 $d_2=0$ ，有

${\tilde{U}}_{S1}^{\pm }\left(\xi \right)=\pm \sqrt{-2l}\cdot \mathrm{sech}\sqrt{\frac{-{\mu }_{3}l}{3}}(\xi -{\xi }_0),$

于是据(3.9)式，有

$l<0,{\mu }_3>0,\Delta <0,m=0$ (3.34)

注意到本文系数与文献 [11] 中系数有下列关系

$h=H(0,0)$ (3.35)

把(3.35)代入(3.34)并化简得

$\{\begin{array}{l}{\tilde{u}}_{S1}^{\pm }\left(x,t\right)={\tilde{U}}_{S1}^{\pm }\left(\xi \right)-\frac{{\mu }_2}{2{\mu }_3},\\ {\tilde{v}}_{S1}^{\pm }\left(x,t\right)=\frac{2}{\epsilon }(c-{\tilde{u}}_{S1}^{\pm }(\xi )),\end{array}$ (3.36)

以上(3.36)式中的 ${\tilde{U}}_{S1}^{\pm }(\xi )$ 与 [11] 中的(9)式完全一致。

这表明，本文不仅得到了以往文献中所求出的方程(1.3)的孤波解，还求出了由定理3.2~定理3.4所给出的方程(1.3)的新孤波解。

4. 方程(1.3)周期波解的求解

正如第二节所指出的，为求方程(1.3)满足关系(2.4)的周期波解，可转化为求方程(2.7)的周期解，而方程(2.7)的周期解，也可通过积分(3.2)并做恰当的变换得到。

4.1. 图1和图6中闭轨对应的精确周期波解

1) 当 ${\mu }_3<0,m>0$ ， $H(d_3,0)=\frac{{\mu }_3}{12}(d_3^4+2l{d}_3^2+4m{d}_3)$ ， $d_3$ 时，对应于图1。系统(2.8)在同宿轨线 $F_h(x)=0$ 和 $m=-d_3^3-l{d}_3$ 所围区域内部的同一闭轨上有相等的Hamilton能量，记为

$F_h(\; x\; )$

其中 $F_h(x)={(x-d_3)}^2(x-{\eta }_1)(x-{\eta }_2),$ 为周期轨线与x轴的交点，并且 ${\eta }_1,{\eta }_2$ 。此时 $F_h(x)=0$ 三个解分别为 $x$ ， ${\eta }_1=-d_3-\sqrt{-2l-2d_3^2}\text{,}{\eta }_2=-d_3+\sqrt{-2l-2d_3^2}$ ， ${\eta }_1<{\eta }_2<d_3.$ ，可得 $({\eta }_2,d_3)$ 。对应的函数曲线和周期轨线如图11所示。

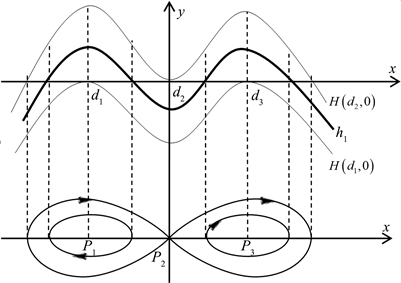
Figure 11. When $U_{S2}^{}(\xi )=d_3-\frac{2(l+3d_3^2)}{2d_3+\sqrt{-2l-2d_3^2}\cosh \sqrt{\frac{{\mu }_3}{3}(l+3d_3^2)}(\xi -{\xi }_0)}.$ , ${\mu }_3<0,m<0$ , $H(d_1,0)$ , corresponding diagram of $F_h(x)={(x-d_1)}^2(x-{\zeta }_1)(x-{\zeta }_2),$ curve family and bounded orbits

图11. ${\zeta }_1,{\zeta }_2$ ， $F_h(x)=0$ ， $x$ 时， ${\zeta }_1=-d_1-\sqrt{-2l-2d_1^2}\text{,}{\zeta }_2=-d_1+\sqrt{-2l-2d_1^2}$ 函数曲线和周期轨线示意图

由于 $d_1<{\zeta }_1<{\zeta }_2.$ ，所以 $(d_1,{\zeta }_1)$ 。在(3.2)式中取 $U_{S3}(\xi )=d_1-\frac{2(l+3d_1^2)}{2d_1-\sqrt{-2l-2d_1^2}\cosh \sqrt{\frac{-{\mu }_3}{3}(l+3d_1^2)}(\xi -{\xi }_0)}.$ ，此时有

$l<0,{\mu }_3<0,\Delta <0$ (4.1)

此时(3.2)式可化为

$m>0$ (4.2)

令 $h=H(d_3,0)$ ， $\{\begin{array}{l}{u}_{S2}^{}(x,t)=U_{S2}^{}(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{S2}^{}(x,t)=\frac{2}{\epsilon }\left(c-u_{S2}^{}(\xi )\right),\end{array}$ ，作变换 $U_{S2}^{}(\xi )$ ，则(4.2)式可转化为

$m<0$ (4.3)

根据椭圆函数积分 [30] [31] 的性质易得如下引理。

引理4.1：若 $H(d_1,0)$ ，则 $\{\begin{array}{l}{u}_{S3}^{}(x,t)=U_{S3}^{}(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{S3}^{}(x,t)=\frac{2}{\epsilon }\left(c-u_{S3}^{}(\xi )\right),\end{array}$ ，其中 $U_{S3}^{}(\xi )$ ( ${\mu }_3>0,\Delta =0,m>0$ 为模数)。

在(4.3)式中令 $d_2=d_3$ ，经计算可得 $\phi (x)=0$ ， $d_1+2d_3=0,2d_1{d}_3+d_3^2=l,d_1{d}_3^2=-m$ ，则(4.3)式两边积分可得

$d_2=d_3=\sqrt{\frac{-l}{3}}$ (4.4)

其中模数 $H(d_3,0)=\frac{{\mu }_3}{12}{d}_3^2(9d_3^2+2l)=\frac{{\mu }_3}{36}{l}^2.$ 。

注： $\Delta =0$ 与 $27m^2+4l^3=0$ 分别表示根号前取“+”，“−”时的解，以下相同。

2) 当 $\Rightarrow$ ， $m=\pm 2(\frac{-l}{3})\sqrt{\frac{-l}{3}}=\pm 2{(\sqrt{\frac{-l}{3}})}^3$ ， $m>0$ 时，对应于图6，系统(2.8)存在对称异宿轨线 $m=2{(\sqrt{\frac{-l}{3}})}^3$ 和 $F_h(x)=x^4+2l{x}^2+4mx-\frac{l^2}{3}={(x-\sqrt{\frac{-l}{3}})}^3(x+3\sqrt{\frac{-l}{3}}).$ ，在 $x\in （-3\sqrt{\frac{-l}{3}},\sqrt{\frac{-l}{3}}）$ 和 $\pm \sqrt{\frac{{\mu }_3}{6}}(\xi -{\xi }_0)={\displaystyle \int \frac{dx}{\sqrt{{(\sqrt{\frac{-l}{3}}-x)}^3(x+3\sqrt{\frac{-l}{3}})}}}=\frac{1}{2}.\sqrt{\frac{3(\sqrt{3}x+3\sqrt{-l})}{l(\sqrt{3}x-\sqrt{-l})}}$ 共同包围区域内部的同一周期轨线上有相等的Hamilton能量

$x$

其中 $U_{S4}^{+}(\xi )=x_{S4}^{+}(\xi )=\sqrt{\frac{-l}{3}}-\frac{12\sqrt{-3l}}{9-2{\mu }_{3}l{(\xi -{\xi }_0)}^2}.$ 为周期轨线与x轴的任一交点， ${\mu }_3>0,\Delta =0,m<0$ ，且可验Hamilton能量满足 $d_1=d_2$ 。对应的函数曲线和周期轨线如图12所示。

Figure 12. When $\phi (x)=0$ , $d_3+2d_1=0,2d_1{d}_3+d_1^2=l,d_3{d}_1^2=-m$ , $d_1=d_2=-\sqrt{\frac{-l}{3}}$ , corresponding diagram of $H(d_1,0)=\frac{{\mu }_3}{12}{d}_1^2(9d_1^2+2l)=\frac{{\mu }_3}{36}{l}^2$ curve family and bounded orbits

图12. 当 $\Delta =0$ ， $27m^2+4l^3=0$ ， $m=-2{(\sqrt{\frac{-l}{3}})}^3$ 时， $F_h(x)=x^4+2l{x}^2+4mx-\frac{l^2}{3}={(x+\sqrt{\frac{-l}{3}})}^3(x-3\sqrt{\frac{-l}{3}}).$ 函数曲线和周期轨线示意图

由于 $x\in （-\sqrt{\frac{-l}{3}},3\sqrt{\frac{-l}{3}}）$ ，所以 $t=\sqrt{\frac{3\sqrt{-l}-\sqrt{3}x}{\sqrt{3}x+\sqrt{-l}}}$ 。在(3.2)式中取 $\pm \sqrt{\frac{{\mu }_3}{6}}(\xi -{\xi }_0)={\displaystyle \int \frac{dx}{\sqrt{{(x+\sqrt{\frac{-l}{3}})}^3(3\sqrt{\frac{-l}{3}}-x)}}}=-\frac{1}{2}\cdot \sqrt{\frac{3(\sqrt{3}x-3\sqrt{-l})}{l(\sqrt{3}x+\sqrt{-l})}}\text{.}$ ，此时有

$x$ (4.5)

此时(3.2)式化为

$U_{S4}^{-}(\xi )=x_{S4}^{-}(\xi )=-\left[\sqrt{\frac{-l}{3}}-\frac{12\sqrt{-3l}}{9-2{\mu }_{3}l{(\xi -{\xi }_0)}^2}\right].$

设 ${\mu }_3>0,l<0,\Delta =0$ ， $m>0$ ，作变换 $H(d_3,0)$ ，则(3.2)式可转化为

$\{\begin{array}{l}{u}_{S4}^{+}(x,t)=U_{S4}^{+}(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{S4}^{+}(x,t)=\frac{2}{\epsilon }\left(c-u_{S4}^{+}(\xi )\right).\end{array}$ (4.6)

根据椭圆函数积分 [30] [31] 的性质易得如下引理。

引理4.2：若 $U_{S4}^{+}(\xi )$ ，则 $m<0$ ，(k为模数)。

对照引理4.2，在(4.6)式中令 $H(d_1,0)$ ，经计算可得 $\{\begin{array}{l}{u}_{S4}^{-}(x,t)=U_{S4}^{-}(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{S4}^{-}(x,t)=\frac{2}{\epsilon }\left(c-u_{S4}^{-}(\xi )\right).\end{array}$ ， $U_{S4}^{-}(\xi )$ ，并注意到Jacobi椭圆函数 ${\mu }_3<0,m=0$ 是奇函数，从而(4.6)式两边积分可得

$d_1$ (4.7)

其中模数 $\phi (x)=x^3+lx=x(x^2+l)=0$ 。

综上，我们可以得到如下定理。

定理4.1：设 $d_1^2=-l$ ， $h=H(d_1,0)$ ， $=\frac{{\mu }_3}{12}(d_1^4+2l{d}_1^2)=-\frac{{\mu }_3}{12}{l}^2$ 。

1) 当 $$ 时，方程(1.3)有周期波解

$F_h(x)=x^4+2l{x}^2-\frac{12}{{\mu }_3}h=x^4+2l{x}^2+l^2={(x+\sqrt{-l})}^2{(x-\sqrt{-l})}^2.$ (4.8)

其中 $\pm \sqrt{-\frac{{\mu }_3}{6}}(\xi -{\xi }_0)={\displaystyle \int \frac{dx}{\sqrt{{(x+\sqrt{-l})}^2{(x-\sqrt{-l})}^2}}}.$ 为方程(2.7)的周期解，由(4.4)式给出。

2) 当 $-\sqrt{-l}<x<\sqrt{-l}$ 时，方程(1.3)有周期波解

$\pm \sqrt{-\frac{{\mu }_3}{6}}(\xi -{\xi }_0)={\displaystyle \int \frac{dx}{(\sqrt{-l}+x)(\sqrt{-l}-x)}}=\frac{-1}{2\sqrt{-l}}\ln \frac{\sqrt{-l}-x}{\sqrt{-l}+x}.$ (4.9)

其中 $x$ 为方程(2.7)的周期解，由(4.7)式给出。

4.2. 图2，图3周期轨线对应的精确周期波解

当 ${\mu }_3>0$ ， $m\ne 0$ ， $\Delta <0$ 时，由于在同宿轨线内包围的同一周期轨线上点有相等的Hamilton能量，有

${\mu }_3<0,l<0,m=0,\Delta <0$ (4.10)

其中 $U_{S5}^{\pm }(\xi )=\pm \sqrt{-l}\tanh (\frac{1}{2}\sqrt{\frac{2{\mu }_{3}l}{3}}(\xi -{\xi }_0)),$ 为周期轨线与x轴的交点， $\{\begin{array}{l}{u}_{S5}^{\pm }(x,t)=U_{S5}^{\pm }(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{S5}^{\pm }(x,t)=\frac{2}{\epsilon }\left(c-u_{S5}^{\pm }(\xi )\right).\end{array}$ 由(2.12)式给定。据图2，图3可知 $d_2=\frac{{\mu }_2}{2{\mu }_3}$ 为系统(2.8)的3个奇点，其横坐标满足 $(u_{S1}^{+}(x,t),v_{S1}^{+}(x,t))$ 。

在 $d_2=\frac{{\mu }_2}{2{\mu }_3}$ 情况，易证 $\phi (x)=x^3+lx+m=0$ ； $l=$ $-\frac{12{\mu }_1{\mu }_3+3{\mu }_2^2}{4{\mu }_3^2}$ 。当Hamilton能量 $l+3d_2^2=-\frac{3{\mu }_1}{{\mu }_3},l+d_2^2=-\frac{2(6{\mu }_1{\mu }_3+{\mu }_2^2)}{4{\mu }_3^2}=-\frac{6{\mu }_1{\mu }_3+{\mu }_2^2}{2{\mu }_3^2}.$ 满足

$u_{S1}^{\pm }(x,t)=\frac{6{\mu }_1}{{\mu }_2\pm \frac{{\mu }_3}{\left|{\mu }_3\right|}\sqrt{{\mu }_2^2+6{\mu }_1{\mu }_3}\cosh [\sqrt{{\mu }_1}(\xi -{\xi }_0)]}.$ (4.11)

此时函数 $a_2={\mu }_1,{\mu }_2=-3a_3,{\mu }_3=-6a_4.$ ((3.2)式中的函数)曲线与x轴有4个不同的交点，即 $u_{S1}^{\pm }(x,t)=\frac{2a_2}{-a_3\pm \sqrt{a_3^2-4a_2{a}_4}\cosh [\sqrt{a_2}(\xi -{\xi }_0)]}.$ 有4个互异实根 $u_{S1}^{+}(x,t)$ ，进而 ${\mu }_3>0,m=0,\Delta <0$可表达为

$L_1$ (4.12)

由于 $x=U\left(\xi \right)$ ， $y=U^{\prime }\left(\xi \right)$ ，所求方程(2.7)的有界解满足 $H(x,y)=H({\eta }_1,0)=\frac{{\mu }_3}{12}{\left({\eta }_1^2+l\right)}^2-\frac{{\mu }_3{l}^2}{12}=h_1,$ ，则在满足条件(4.11)的情况下，由(3.2)式可求得下列两类周期波解。

(i) 当 $({\eta }_1,0)$ 时，作变换

$x$

代入(3.2)式，可得

$\left|{\eta }_1\right|<\sqrt{-l}$

这里 $\phi \left(x\right)=x(x^2+l)=0$ 。由Jacobi椭圆函数定义以及函数 $d_1=-\sqrt{-l},d_2=0,d_3=\sqrt{-l}$ 为奇函数性质，可知

$H\left(d_1,0\right)=H\left(d_3,0\right)$

可得方程(2.7)的有界解

$<H\left(d_2,0\right)$ (4.13)

(ii) 当 ${\mu }_3>0,m=0,\Delta <0$ 时，作变换

$-F_{h_1}(x)$ ,

与情形(i)类似可得到方程(2.7)的有界解

${\mu }_3>0,m=0,\Delta <0$ (4.14)

综上可得如下定理4.2。

定理4.2：设 $h_1$ ， $-F_{h_1}(x)$ ， $H({\eta }_1,0)=\frac{{\mu }_3}{12}{({\eta }_1{}^2+l)}^2-\frac{{\mu }_3{l}^2}{12}=h_1$ ， $-\frac{{\mu }_3{l}^2}{12}<h_1<0$ 成立，当Hamilton能量h满足(4.11)时，方程(1.3)有两个周期波解

$h=h_1$ (4.15)

和

$-F_{h_1}(x)=-(x^4+2l{x}^2-\frac{12h_1}{{\mu }_3})=l^2+\frac{12h_1}{{\mu }_3}-{(x^2+l)}^2,$ (4.16)

其中 $\pm \sqrt{\frac{{\mu }_3}{6}}d\xi =\frac{dx}{\sqrt{l^2+\frac{12h_1}{{\mu }_3}-{(x^2+l)}^2}}$ 和 $=\frac{dx}{\sqrt{-(x^2+l+\sqrt{l^2+\frac{12h_1}{{\mu }_3}})(x^2+l-\sqrt{l^2+\frac{12h_1}{{\mu }_3}})}}.$ 为方程(2.7)的有界解，分别由(4.13)和(4.14)式给出。

4.3. 图7，图8周期轨线对应的精确周期波解

当 $A_1{}^2=\sqrt{l^2+\frac{12h_1}{{\mu }_3}}-l,B_1{}^2=-\sqrt{l^2+\frac{12h_1}{{\mu }_3}}-l$ ， $t=\frac{x}{A_1}=\frac{U(\xi )}{A_1}$ ， $\pm \sqrt{\frac{{\mu }_3}{6}}d\xi =\frac{dx}{\sqrt{-\left(x^2-A_1^2\right)\left(x^2-B_1^2\right)}}=\frac{dt}{A_1\sqrt{[1-t^2]\cdot [t^2-{(\frac{B_1}{A_1})}^2]}}$ 时，由于在同宿轨线 ${\displaystyle \int \frac{dt}{\sqrt{\left(1-t^2\right)\left(t^2-{k^{\prime }}^2\right)}}}=u$ 内包围的同一周期轨线上点有相等的Hamilton能量，有

$t=\text{dn}\left(u,k_1\right)$ (4.17)

其中 $k_1^2+{k^{\prime }}^2=1$ 为周期轨线与x轴的交点。当Hamilton能量 $k_1$ 满足如下条件

${k^{\prime }}_1=\frac{\left|B_1\right|}{\left|A_1\right|}$ (4.18)

时(可证： $A_1^2=\frac{-2l}{2-k_1^2}$ 时， $B_1^2=\frac{-2l(1-k_1^2)}{2-k_1^2}$ 有 $U_{P1}^{\pm }(\xi )=\pm \sqrt{\frac{-2l}{2-k_1^2}}\cdot \text{dn}(\sqrt{\frac{-{\mu }_{3}l}{3(2-k_1^2)}}(\xi -{\xi }_0),k_1),$ ， $k_1^2=\frac{2\sqrt{{\mu }_3{l}^2+12h_1}}{\sqrt{{\mu }_3{l}^2+12h_1}-\sqrt{{\mu }_3}l}$ 有 $U_{p_1}^{+}(\xi )$ )，函数 $U_{p_1}^{-}(\xi )$ ((3.2)式)的函数曲线与x轴有4个不同的交点，即 $-$ 有4个互异实根 ${\mu }_3<0,m=0,\Delta <0$ , 从而 $L_9$ 表达为(4.12)式。对应的函数曲线和周期轨线如图13所示。

(i) 当 $L_{10}$ ，Hamilton能量 $L_9$ 满足条件 $L_{10}$ 时，作变换

$H(x,y)=H({\eta }_2,0)=\frac{{\mu }_3}{12}{\left({\eta }_2^2+l\right)}^2-\frac{{\mu }_3{l}^2}{12}=h_2,$

可得方程(2.7)的有界解

$({\eta }_2,0)$ (4.19)

这里 $x$ 。

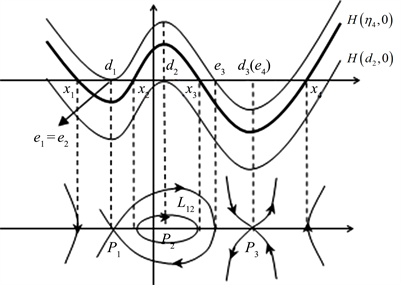
Figure 13. When $\left|{\eta }_2\right|<\sqrt{-l}$ , $H\left(d_1,0\right)$ , $=H\left(d_3,0\right)>H\left(d_2,0\right)$ , corresponding diagram of ${\mu }_3<0,m=0,\Delta <0$ curve family and bounded orbits

图13. 当 $-F_{h_2}(x)$ ， ${\mu }_3<0,m=0,\Delta <0$ ， $h_2$ 时， $-F_{h_2}(x)$ 函数曲线和周期轨线示意图

(ii) 当 $H({\eta }_2,0)=\frac{{\eta }_3}{12}{({\eta }_2^2+l)}^2-\frac{{\mu }_3{l}^2}{12}=h_2$ ，Hamilton能量 $0<h_2<-\frac{{\mu }_3{l}^2}{12}$ 满足条件 $h=h_2$ 时，作变换

$F_h{}_{{}_2}(x)=x^4+2l{x}^2-\frac{12h_2}{{\mu }_3}={(x^2+l)}^2-(l^2+\frac{12h_2}{{\mu }_3}),$

可得方程(2.7)的有界解

$\pm \sqrt{-\frac{{\mu }_3}{6}}d\xi =\frac{dx}{\sqrt{{(x^2+l)}^2-(l^2+\frac{12h_2}{{\mu }_3})}}$ (4.20)

这里 $A_2^2=\sqrt{l^2+\frac{12h_2}{{\mu }_3}}-l,B_2^2=-\sqrt{l^2+\frac{12h_2}{{\mu }_3}}-l$ 。

综上，我们可以得到如下定理。

定理4.3：设 $t=\frac{x}{A_2}=\frac{U(\xi )}{A_2}$ ， $\pm \sqrt{-\frac{{\mu }_3}{6}}d\xi =\frac{dt}{B_2\sqrt{[1-t^2]\cdot [1-{(\frac{A_2}{B_2})}^2{t}^2]}}$ ， ${\displaystyle \int \frac{dt}{\sqrt{\left(1-t^2\right)\left(1-k^2{t}^2\right)}}}=u$ ， $t=\text{sn}\left(u,k\right)$ 成立，Hamilton能量h满足(4.18)。

1) 当 $k$ 时，方程(1.3)有周期波解

$k_2=\left|\frac{A_2}{B_2}\right|$ (4.21)

其中 $A_2^2=\frac{-2l{k}_2^2}{1+k_2^2},B_2^2=\frac{-2l}{1+k_2^2}$ 为方程(2.7)的有界解，由(4.19)式给出。

2) 当 $\text{sn}(u,k)$ 时，方程(1.3)有周期波解

$U_{P2}^{\pm }\left(\xi \right)=\pm \sqrt{\frac{-2l{k}_2^2}{1+k_2^2}}\cdot \text{sn}(\sqrt{\frac{{\mu }_{3}l}{3(1+k_2^2)}}\xi ,k_2)$ (4.22)

其中 $k_2^2=\frac{{\mu }_{3}l+\sqrt{12{\mu }_3{h}_3+3l^2{\mu }_3^2}}{{\mu }_{3}l-\sqrt{12{\mu }_3{h}_3+3l^2{\mu }_3^2}}$ 为方程(2.7)的有界解，由(4.20)式给出。

4.4. 图1~5其余周期轨线对应的周期波解

当 $l<0,\Delta <0,m=0$ 时，在图1~5上还存在：包围同宿轨线 ${\mu }_3>0$ 的周期轨线， $\{\begin{array}{l}{u}_{P1}^{\pm }(\xi )=U_{P1}^{\pm }(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{P1}^{\pm }(\xi )=\frac{2}{\epsilon }(c-u_{P1}^{\pm }(\xi )).\end{array}$ 和 $U_{P1}^{\pm }(\xi )$ 包围着的周期轨线以及 ${\mu }_3<0$ 和 $\{\begin{array}{l}{u}_{P2}^{\pm }(\xi )=U_{P2}^{\pm }(\xi )-\frac{{\mu }_2}{2{\mu }_3}\\ v_{P2}^{\pm }(\xi )=\frac{2}{\epsilon }(c-u_{P2}^{\pm }(\xi ))\end{array}$ 内部位于中心点附近包围中心的周期轨线。这些周期轨线可归为一类，其特点是与x轴的交点仅有两个。

以 ${\mu }_3>0$ ， $\Delta <0$ ， $m<0$ 情况为例( ${\mu }_3>0,m\ne 0,\Delta <0$ 的其他情况类似)。如图14所示，当Hamilton能量 $H\left(x,y\right)=H\left({\eta }_3,0\right)=h_3$ 的取值范围为： $({\eta }_3,0)$ 或 $x$ 值介于 $H\left(x,y\right)$ 和 $P(d_i,0)\left(i=1,2,3\right)$ 之间时，(3.2)式取函数

$d_1<d_2<d_3$ (4.23)

${\mu }_3>0$ 与x轴有2个不同的交点 $m>0,H(d_1,0)<H(d_3,0)<H(d_2,0)$ 。此时(4.23)式可表示为

$m<0,$ (4.24)

其中 $H(d_3,0)<H(d_1,0)$ ， $<H(d_2,0)$ 。

Figure 14. When $h_3$ , $\max \{H(d_1,0),H(d_3,0)\}<h_3<H(d_2,0)$ , $x$ , corresponding diagram of $x_1<d_1<x_2<d_2<x_3<d_3<x_4$ curve family and bounded orbits

图14. $F_h(x)=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right).$ ， $x=U(\xi ),y=U^{\prime }(\xi )$ ， ${(\frac{dU}{d\xi })}^2=-\frac{{\mu }_3}{6}{F}_h(U)$ 时， $x_1<U<x_2$ 函数曲线和周期轨线示意图

将(4.24)式拆分为

$U=\frac{x_4\left(x_2-x_1\right){\sin }^2\varphi +x_1\left(x_4-x_2\right)}{\left(x_2-x_1\right){\sin }^2\varphi +x_1\left(x_4-x_2\right)}$ (4.25)

$\sqrt{\frac{{\mu }_3}{6}}(\xi -{\xi }_0)=\frac{-2}{\sqrt{\left(x_4-x_2\right)\left(x_3-x_1\right)}}{\displaystyle \int \frac{d\varphi }{\sqrt{1-k_3^2{\sin }^2\varphi }}}$ (4.26)

其中 $k_3^2=\frac{\left(x_4-x_3\right)\left(x_2-x_1\right)}{\left(x_4-x_2\right)\left(x_3-x_1\right)}$ ， $sn(u,k)$ ， $\text{sn}(\sqrt{\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_3)=-\sin \varphi$ ，而 $U_{P3}(\xi )=\frac{x_4\left(x_2-x_1\right){\text{sn}}^2(\frac{1}{2}\sqrt{\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_3)+x_1\left(x_4-x_2\right)}{\left(x_2-x_1\right){\text{sn}}^2(\frac{1}{2}\sqrt{\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_3)+\left(x_4-x_2\right)}$ 是方程

$x_3<U<x_4$ (4.27)

的两个实根。由于 $U=\frac{x_1\left(x_4-x_3\right){\sin }^2\varphi +x_4(x_3-x_1)}{\left(x_4-x_3\right){\sin }^2\varphi +(x_3-x_1)}$ ， $U_{P4}=\frac{x_1\left(x_4-x_3\right){\mathrm{sn}}^2(\frac{1}{2}\sqrt{\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_3)+x_4(x_3-x_1)}{\left(x_4-x_3\right){\mathrm{sn}}^2(\frac{1}{2}\sqrt{\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_3)+(x_3-x_1)}$ ，令 $l<0,\Delta <0,{\mu }_3>0$ ，由(3.2)式可得

$m\ne 0$

再令 $\{\begin{array}{l}{u}_{P3}\left(\xi \right)=U_{P3}\left(\xi \right)-\frac{{\mu }_2}{2{\mu }_3},\\ v_{P3}\left(\xi \right)=\frac{2}{\epsilon }(c-u_{P3}\left(\xi \right)).\end{array}$ 和 $\{\begin{array}{l}{u}_{P4}\left(\xi \right)=U_{P4}\left(\xi \right)-\frac{{\mu }_2}{2{\mu }_3},\\ v_{P4}\left(\xi \right)=\frac{2}{\epsilon }(c-u_{P4}\left(\xi \right)).\end{array}$ ，得

$U_{P3}\left(\xi \right)\in (x_1,x_2)$

由Jacobi椭圆函数积分，计算可得

$U_{P4}\left(\xi \right)\in (x_3,x_4)$

化简可得到方程(2.7)的有界解

${\mu }_3<0,m\ne 0,\Delta <0$ (4.28)

其中 $L_i(i=11,12)$ ， $H(x,y)=H({\eta }_4,0)=h_4$ 满足方程(4.27)， $({\eta }_4,0)$ 由下式给出

$x$ (4.29)

特别指出

1) 当 $h_4$ ， $H(d_2,0)<h_4<\min \{H(d_1,0),H(d_3,0)\}$ ， ${\mu }_3<0$ 时，此时(4.25)式为

$m>0$ (4.30)

此时直接将(4.30)式代入(3.2)式，求积分得到图1中包围同宿轨线 $H(d_2,0)<H(d_3,0)<H(d_1,0)$ 和 $m<0$ 的周期轨线所对应的方程(2.7)的有界解为

$H(d_2,0)<H(d_1,0)<H(d_3,0)$ (4.31)

其中 $x$ 。

2) 对比(4.23)和(4.24)式，可得 $x_1<d_1<x_2<d_2<x_3<d_3<x_4$ ， $m<0$ 以及 $h_4$ 。

当 $H(d_2,0)<h_4<H(d_1,0)$ ， $U=\frac{x_3\left(x_4-x_2\right)-x_4\left(x_3-x_2\right){\sin }^2\varphi }{\left(x_4-x_2\right)-\left(x_3-x_2\right){\sin }^2\varphi }$ 时，有 $U_{P5}\left(\xi \right)=\frac{x_3\left(x_4-x_2\right)-x_4(x_3-x_2){\mathrm{sn}}^2(\frac{1}{2}\sqrt{-\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_4)}{\left(x_4-x_2\right)-(x_3-x_2){\mathrm{sn}}^2(\frac{1}{2}\sqrt{-\frac{{\mu }_3}{6}\left(x_4-x_2\right)\left(x_3-x_1\right)}(\xi -{\xi }_0),k_4)}$ ，即 $k_4^2=\frac{(x_4-x_1)(x_3-x_2)}{(x_4-x_2)(x_3-x_1)}$ ，且

${\mu }_3<0,m<0,\Delta <0$

此时(4.28)式对应于系统(2.8)的包围同宿轨线 $-F_{h_4}(x)$ 的周期轨线。

当 ${\mu }_3<0,m<0,\Delta <0$ ， $h_4$ 时，得 $-F_{h_4}(x)$ ，且

$m>0$

此时(4.28)式对应于系统(2.8)的 $h_4$ 包围着的周期轨线，以及 $H(d_2,0)<h_4<H(d_3,0)$ 和 $U=\frac{x_2(x_3-x_1)-x_1(x_3-x_2){\sin }^2\varphi }{(x_3-x_1)-(x_3-x_2){\sin }^2\varphi }$ 内部位于中心点附近包围中心的周期轨线。

综上，我们可以得到如下定理。

定理4.4 若条件(1)： $U_{P6}(\xi )=\frac{x_2(x_3-x_1)-x_1(x_3-x_2){\text{sn}}^2(\sqrt{-\frac{{\mu }_3}{6}(x_4-x_2)(x_3-x_1)}(\xi -{\xi }_0),k_4)}{(x_3-x_1)-(x_3-x_2){\text{sn}}^2(\sqrt{-\frac{{\mu }_3}{6}(x_4-x_2)(x_3-x_1)}(\xi -{\xi }_0),k_4)}$ ， $k_4^2=\frac{(x_4-x_1)(x_3-x_2)}{(x_4-x_2)(x_3-x_1)}$ ，Hamilton能量 $l<0,\Delta <0,{\mu }_3<0,m\ne 0$ 或 $m<0$ 成立，或条件(2)： $\{\begin{array}{l}{u}_{P5}\left(\xi \right)=U_{P5}\left(\xi \right)-\frac{{\mu }_2}{2{\mu }_3},\\ v_{P5}\left(\xi \right)=\frac{2}{\epsilon }(c-u_{P5}\left(\xi \right)).\end{array}$ ， $U_{P5}(\xi )\in \left(x_2,x_3\right)$ ， $m>0$ ，且Hamilton能量 $\{\begin{array}{l}{u}_{P6}(\xi )=U_{P6}(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{P6}\left(\xi \right)=\frac{2}{\epsilon }(c-u_{P6}(\xi )).\end{array}$ 成立，则方程(2.7)有周期解 $U_{P6}(\xi )\in (x_{\text{2}},x_{\text{3}})$ ，由(4.28)给定，从而方程(1.3)有周期波解

${\mu }_3>0$ (4.32)

5. Hamilton能量与方程(1.3)的周期波解和孤波解的关系

5.1. 方程(1.3)的周期波解和孤波解与Hamilton能量取极限的关系

5.1.1. 图1对称同宿轨内周期波解与孤波解的演变关系

当 $L_i(i=1,2，\cdots ,8)$ ， $L_7$ ， $L_8$ 时，全局相图1有对称同宿轨 $L_3$ 和 $L_6$ 。在第三节我们已求得 $x$ 和 ${\mu }_3>0,\Delta <0,m<0$ 对应的方程(1.3)的孤波解 ${\mu }_3<0$ ，它们由(3.12)给出。同宿轨 $h_5$ 和 $h_5>H(d_2,0)$ 内闭轨对应的周期波解由定理4.1结论(1)给出。由定理4.1结论(1)知，方程(1.3)的周期波解 $h_5$ 中 $H(d_1,0)$ 对应的Hamilton能量

$H(d_3,0)$ ， $-F_h(x)=-x^4-2l{x}^2-4mx+\frac{12h_5}{{\mu }_3},$ ，而孤波解(3.12)式中 $-F_h(x)$ 对应的Hamilton能量此时为 $x$ ，当 ${\gamma }_2<{\gamma }_1$ ， $-F_h\left(x\right)=\left({\gamma }_1-x\right)\left(x-{\gamma }_2\right)\left({\left(x-\alpha \right)}^2+{\beta }^2\right)$ ，所以方程(1.3)的周期波解 $2\alpha +{\gamma }_1+{\gamma }_2=0,\beta >0.$ 在 ${\mu }_3>0,\Delta <0,m<0$ 时有

$-F_{h_5}(x)$ (5.1a)

故有

${\mu }_3>0,\Delta <0,m<0$ (5.1b)

即当Hamilton能量 $h_5$ 时，方程(1.3)的周期波解演变为钟状孤波解 $-F_{h_5}(x)$ 。

5.1.2. 非对称同宿轨内周期波解和孤波解的演变关系

这里仅讨论图3和图8两种情形，其余情形的讨论类似。

1) 在图3情形

此时 ${\mu }_3>0$ ， $\Delta <0$ ， $m<0$ 。当Hamilton能量 $\left({\gamma }_1-x\right)\left(x-{\gamma }_2\right)={\epsilon }_2{\left(x-{\sigma }_1\right)}^2-\left(1+{\epsilon }_2\right){\left(x-{\sigma }_2\right)}^2,$ 时，有同宿轨线 ${\sigma }_i=\alpha \frac{1-{\lambda }_i}{1+{\lambda }_i},\left(i=1,2\right),{\epsilon }_1=\frac{{\lambda }_2\left(1+{\lambda }_1\right)}{{\lambda }_2-{\lambda }_1},{\epsilon }_2=\frac{1+{\lambda }_1}{{\lambda }_2-{\lambda }_1}$ 与 ${\lambda }_1,{\lambda }_2$ ，它们对应的方程(1.3)的钟状孤波解 ${\left({\gamma }_1-{\gamma }_2\right)}^2{\lambda }^2-4\left({\beta }^2+\left(\alpha -{\gamma }_1\right)\left(\alpha -{\gamma }_2\right)\right)\lambda -4{\beta }^2=0$ 由(3.10)式给出。当Hamilton能量 $x=U(\xi ),y=U^{\prime }(\xi )$ 时，系统(2.8)存在同宿轨线包围着的周期轨线，相应的周期波解为 $s=\frac{x-{\sigma }_1}{x-{\sigma }_2}=\frac{U(\xi )-{\sigma }_1}{U(\xi )-{\sigma }_2}$ 、 $\pm \sqrt{\frac{{\mu }_3}{6}}(\xi -{\xi }_0)=\frac{1}{\left({\sigma }_1-{\sigma }_2\right)\sqrt{{\epsilon }_1{\epsilon }_2}}{\displaystyle \int \frac{ds}{\sqrt{(s^2+\frac{1-{\epsilon }_1}{{\epsilon }_1})(s^2-(\frac{1+{\epsilon }_2}{{\epsilon }_2}))}}}$ ， $s^2=\frac{1+{\epsilon }_2}{{\epsilon }_2\left(1-t^2\right)}$ 与 $k_5^2=\frac{{\epsilon }_2\left(1-{\epsilon }_1\right)}{{\epsilon }_1+{\epsilon }_2}$ 分别由(4.15)和(4.16)式给出。此时，系统(2.8)有3个奇点 $\pm \sqrt{\frac{{\mu }_3}{6}\left({\epsilon }_2+{\epsilon }_1\right)}\left({\sigma }_1-{\sigma }_2\right)(\xi -{\xi }_0)={\displaystyle \int \frac{dt}{\sqrt{\left(1-t^2\right)\left(1-k_5^2{t}^2\right)}}}.$ , 其中 $U\left(\xi \right)={\sigma }_1-\frac{{\sigma }_1-{\sigma }_2}{1\pm \sqrt{\frac{{\epsilon }_2}{1+{\epsilon }_2}}\cdot \text{cn}(\sqrt{\frac{{\mu }_3}{6}\left({\epsilon }_2+{\epsilon }_1\right)}\left({\sigma }_1-{\sigma }_2\right)(\xi -{\xi }_0),k_5)}.$ 可表示为

$U_{P7}^{\pm }\left(\xi \right)=\frac{1-{\lambda }_1}{1\text{+}{\lambda }_1}\alpha -\frac{\rho }{2\alpha \pm 2\alpha \sqrt{\frac{1+{\lambda }_1}{1+{\lambda }_2}}\cdot \text{cn}\left(\sqrt{\frac{{\mu }_3\rho }{6}}(\xi -{\xi }_0),k_5\right)},$ (5.2)

当 $\rho =\sqrt{[{\beta }^2+{(\alpha -{\gamma }_1)}^2][{\beta }^2+{(\alpha -{\gamma }_2)}^2]}$ 时，(3.2)式中函数 ${\lambda }_1<{\lambda }_2$ 与x轴的交点横坐标为

$k_5$ (5.3)

显然， $k_5^2=\frac{1}{2}-\frac{{\beta }^2\text{+}(\alpha -{\gamma }_1)(\alpha -{\gamma }_{\text{2}})}{2\sqrt{[{\beta }^2+{(\alpha -{\gamma }_1)}^2][{\beta }^2+{(\alpha -{\gamma }_2)}^2]}}.$ 与 ${\mu }_3>0,\Delta <0,m=0$ 有关系： $-F_h(x)=(-l+\sqrt{l^2+\frac{12h_5}{{\mu }_3}}-x^2)(l+\sqrt{l^2+\frac{12h_5}{{\mu }_3}}+x^2).$ 。当Hamilton能量 $L_1$ 时，位于两个同宿轨内的周期轨线与x轴的交点的横坐标 $L_2$ 满足方程

${\tilde{U}}_{P7}^{\pm }\left(\xi \right)=\pm \sqrt{\frac{-2l{\tilde{k}}_1^2}{2{\tilde{k}}_1^2-1}}\cdot \text{cn}(\sqrt{\frac{-{\mu }_{3}l}{3(2{\tilde{k}}_1^2-1)}}(\xi -{\xi }_0),{\tilde{k}}_1),$

且

${\tilde{k}}_1^2=\frac{\sqrt{{\mu }_3}l+\sqrt{{\mu }_3{l}^2+12h_4}}{2\sqrt{{\mu }_3{l}^2+12h_4}}\in \left(\frac{1}{2},1\right]$

由于函数 $2\alpha +{\gamma }_1+{\gamma }_2=0$ 关于能量h具连续性，故 $2l={\beta }^2-\text{3}{\alpha }^{\text{2}}+{\gamma }_1{\gamma }_2$ 的零点 $4m=\text{2}\alpha ({\alpha }^2\text{+}{\beta }^2-{\gamma }_1{\gamma }_2)$ 关于h也具连续性，于是，当 ${\beta }^2\text{+}(\alpha -{\gamma }_1)(\alpha -{\gamma }_{\text{2}})<0$ 时， $k_5^2>\frac{1}{2}$ ， ${\beta }^2\text{+}(\alpha -{\gamma }_1)(\alpha -{\gamma }_{\text{2}})={\beta }^2\text{+}3{\alpha }^2+{\gamma }_1{\gamma }_{\text{2}}=2l+6{\alpha }^2$ ， $=2(l+3{\alpha }^2)<0$ ， ${(\frac{{\gamma }_1+{\gamma }_2}{2})}^2<\frac{-l}{3}$ ，且模数 ${\gamma }_2<d_1=\frac{-d-\sqrt{-3d^2-4l}}{2}<d_2=d<d_3$ 。由此可得

$=\frac{-d+\sqrt{-3d^2-4l}}{2}$

同理可得 $<{\gamma }_1$ 。

故当 $L_i(i=1,2,\cdots ,8)$ 时，方程(1.3)的周期波解 ${\beta }^2\text{+}(\alpha -{\gamma }_1)(\alpha -{\gamma }_{\text{2}})>0$ 和 $k_5^2<\frac{1}{2}$ 分别趋于钟状孤波解 ${(\frac{{\gamma }_1+{\gamma }_2}{2})}^2>\frac{-l}{3}$ 和 $d_1=d<d_2=\frac{-d-\sqrt{-3d^2-4l}}{2}$ 。

2) 在图8情形

此时 ${\mu }_3<0$ ， $\Delta <0$ ， $m<0$ ，如图13所示，当Hamilton能量 $L_7,L_8$ 时， $L_3$ 与x轴有3个交点，且满足 $L_6$ ，此时方程(2.7)有对应于同宿轨 ${\mu }_3>0,\Delta <0$ 的钟状解(3.18)，而当Hamilton能量 $h>H(d_2,0)$ 时，方程(2.7)有周期解 $h\in \left(H(d_3,0),H(d_1,0)\right)$ ，由(4.19)式给出。此时函数 ${\mu }_3>0,l<0,\Delta =0$ 与x轴有4个交点，这些交点的横坐标 $h\ne H(d_2,0)$ 与 $U_{P7}^{\pm }(\xi )$ 有关系(如图13所示)

$\{\begin{array}{l}{u}_{P7}^{\pm }(\xi )=U_{P7}^{\pm }(\xi )-\frac{{\mu }_2}{2{\mu }_3},\\ v_{P7}^{\pm }\left(\xi \right)=\frac{2}{\epsilon }(c-u_{P7}^{\pm }(\xi )).\end{array}$

故由函数的连续性知，当 ${\mu }_3>0,\Delta <0,m=0$ 时， $L_1$ ， $L_2$ ， $L_1$ ， $L_2$ ，且模数 $({\tilde{u}}_{S1}^{\pm },{\tilde{v}}_{S1}^{\pm })$ 。

$L_1$

故当 $L_2$ 时，方程(1.3)的周期波解 $(u_{P1}^{\pm }(\xi ),v_{P1}^{\pm }(\xi ))$ 演化成 $U_{P1}^{\pm }(\xi )$ 。

5.1.3. 包围同宿轨的闭轨对应的周期波解与孤波解的极限关系

本段中，我们仅以图3中包围同宿轨的闭轨为例来进行讨论，其余情形类似。

此时 $h\in (-\frac{{\mu }_3{l}^2}{12},0)$ ， $k_1^2=\frac{2\sqrt{{\mu }_3{l}^2+12h}}{\sqrt{{\mu }_3{l}^2+12h}-\sqrt{{\mu }_3}l}$ ， $l<0$ 。当Hamilton能量 ${\tilde{U}}_{S1}^{\pm }$ 时，同宿轨线 $H(d_2,0)=0$ ， $k_1^2=\frac{2\sqrt{{\mu }_3{l}^2}}{\sqrt{{\mu }_3{l}^2}-\sqrt{{\mu }_3}l}\to 1$ 对应的方程(1.3)的钟状孤波解为 $(u_{P1}^{\pm }(\xi ),v_{P1}^{\pm }(\xi ))$ ，它由(3.10)式给出。当 $\underset{h\to 0^{-}}{\lim }{U}_{P1}^{\pm }(\xi )=\underset{k_1\to 1}{\lim }\pm \sqrt{\frac{-2l}{2-k_1{}^2}}\text{dn(}\sqrt{\frac{-{\mu }_{3}l}{3(2-k_1{}^2)}}\xi ,k_1)=\pm \sqrt{-2l}\cdot \mathrm{sech}(\sqrt{\frac{-{\mu }_{3}l}{3}}\xi )={\tilde{U}}_{S1}^{\pm }(\xi ),$ 时，系统(2.8)存在包围同宿轨线 $\underset{h\to 0^{-}}{\lim }(u_{P1}^{\pm }(\xi ),v_{P1}^{\pm }(\xi ))=({\tilde{u}}_{S1}^{\pm }(\xi ),{\tilde{v}}_{S1}^{\pm }(\xi )),$ 和 $h\to H{(d_2,0)}^{-}$ 的闭轨，它对应的周期波解 $({\tilde{u}}_{S1}^{\pm }(\xi ),{\tilde{v}}_{S1}^{\pm }(\xi ))$ 由(4.28)式给出。

此时有 ${\mu }_3>0,\Delta <0,m<0$ ，即 $h=H(d_2,0)$ ，相应地(4.29)式的 $L_5$ ，周期轨与x轴的交点横坐标 $L_6$ 满足

$(u_{S1}^{\pm }(\xi ),v_{S1}^{\pm }(\; \xi \; )\; )$

当 $h\in (H(d_1,0),H(d_2,0))$ 时，有

$(u_{P3}(\xi ),v_{P3}(\; \xi \; )\; )$

$(u_{P4}(\xi ),v_{P4}(\; \xi \; )\; )$

$L_5$

由此可得

$L_6$

故当 $P_i(d_i,0),(i=1,2,3)$ 时，方程(1.3)的包围同宿轨线的周期波解 $d_i(i=1,2,3)$ 演化成钟状孤波解 $d_1=\frac{-d_2-\sqrt{-3d_2^2-4l}}{2},d_2,d_3=\frac{-d_2+\sqrt{-3d_2^2-4l}}{2}$ 。

5.2. 周期波解向孤波解演变的三维示意图

1) 当 ${\mu }_3>0$ ， $l<0$ ， $m<0$ ， $\Delta <0$ 时，对应于全局相图3，由前面的讨论可知，当 $Y=-F_h(x)$ 时，方程(1.3)有钟状孤波解 $x$ 。当 $e_1=-d_2-\sqrt{-2l-2d_2^2},e_2=e_3=d_2,e_4=-d_2+\sqrt{-2l-2d_2^2}$ 时，方程(1.3)有周期波解 $d_i(i=1,2,3)$ 和 $e_j(j=1,\cdots ,4)$ ，且当 $e_1<d_1<e_2=e_3=d_2<d_3<e_4$ 时有 $h\in (H(d_1,0),H(d_2,0))$ ， $x$ 。由于这两个周期波解演变为孤波解时具类似性， $x_i(i=1,\cdots ,4)$ 与 $-F_h(x)=-x^4-2l{x}^2-4mx+\frac{12h}{{\mu }_3}=0$ 又有关系式(2.4)，故我们只需画出当 $e_1<x_1<x_2<e_2=e_3<x_3<x_4<e_4$ 时， $-F_h(x)$ 演变为 $h$ 的示意图即可。现令 ${\mu }_3=4$ ， $l=-3$ ， $m=-1$ ， $c=1$ ， $\epsilon =2$ ，此时 $x_i$ ， $h$ 。当Hamilton能量 $h\to H^{-}(d_2,0)$ 时， $x_1\to e_1,x_2\to e_2=d_2,x_3\to e_3=d_2,x_4\to e_4$ 演变为 $k_3\to 1$ 的三维示意图如图15~18所示：

Figure 15. When $\underset{h\to H^{-}(d_2,0)}{\lim }{U}_{P4}(\xi )=\underset{k_3\to 1}{\lim }{U}_{P4}(\xi )$ , the diagram of $=\frac{e_1(e_4-e_2){\mathrm{sech}}^2(\frac{1}{4}\sqrt{\frac{2{\mu }_3}{3}(e_4-e_2)(e_2-e_1)}\xi )+e_4(e_2-e_1)}{(e_4-e_2){\mathrm{sech}}^2(\frac{1}{4}\sqrt{\frac{2{\mu }_3}{3}(e_4-e_2)(e_2-e_1)}\xi )+(e_2-e_1)}$

图15. $=d_2-\frac{\sqrt{2}(l+3d_2^2)}{\sqrt{2}{d}_2+\sqrt{-l-d_2^2}\cdot \cosh (\sqrt{-\frac{2{\mu }_3}{3}(l+3d_2^2)}\xi )}=U_{S1}^{+}(\xi )$ 时 $\underset{h\to H^{-}(d_2,0)}{\lim }{U}_{P3}^{}(\xi )=\underset{k_3\to 1}{\lim }{U}_{P3}^{}(\xi )=U_{S1}^{-}(\xi )$ 图像

Figure 16. When $h\to H^{-}(d_2,0)$ , the diagram of $(u_{P3}(\xi ),v_{P3}(\; \xi \; )\; )$

图16. $(u_{P4}(\xi ),v_{P4}(\xi ))$ 时 $(u_{S1}^{-}(\xi ),v_{S1}^{-}(\xi ))$ 图像

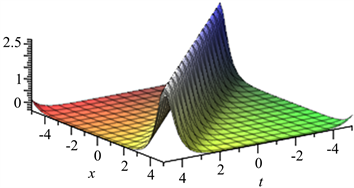
Figure 17. When $(u_{S1}^{+}(\xi ),v_{S1}^{+}(\xi ))$ , the diagram of ${\mu }_3<0,\Delta <0,m<0$

图17. $h=H(d_1,0)$ 时 $Y=F_h(x)$ 图像

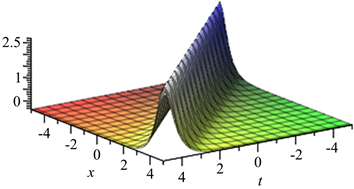
Figure 18. When $x$ , the diagram of $e_1=e_2=d_1<e_3<e_4$

图18. $L_{12}$ 时 $h\in (H(d_2,0),H(d_1,0))$ 图像

2) 当 ${\mu }_3<0$ ， $l<0$ ， $m=0$ ， $\Delta <0$ 时，对应于图6，当 $F_h(x)$ 时，方程(1.3)有扭状孤波解 $x$ ，当 $x_i$ 时，方程(1.3)有周期波解 $e_i(i=1,2,3,4)$ 。且有 $x_1<e_1=e_2<x_2<e_3<x_3<e_4<x_4$ ， $h\to H(d_1,0)$ 。我们只需画出当 $x_1\to e_1,x_2\to e_2,x_3\to e_3,x_4\to e_4$ 时， $k_4\to 1$ 演变为 $\underset{h\to H(d_1,0)}{\lim }{U}_{P5}(\xi )=\underset{k_4\to 1}{\lim }{U}_{P5}(\xi )$ 的示意图。令 ${\mu }_3=-4$ ， $l=-3$ ， $m=0$ ， $c=1$ ， $\epsilon =2$ ，此时 $=d_1-\frac{\sqrt{2}(l+3d_1^2)}{\sqrt{2}{d}_1-\sqrt{-l-d_1^2}\cdot \text{cosh}(\sqrt{-\frac{2{\mu }_3}{3}(l+3d_1^2)}\xi )}=U_{S3}^{}(\xi )$ 。当Hamilton能量 $h\to H(d_1,0)$ 时， $(u_{P5}(\xi ),v_{P5}(\xi ))$ 演变为 $(u_{S3}(\xi ),v_{S3}(\xi ))$ 的三维示意图如图19~22所示：

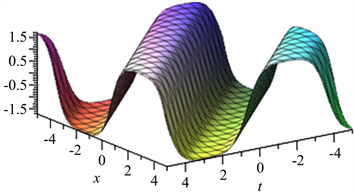
Figure 19. When ${\mu }_3>0,\Delta <0,m<0$ , the diagram of $h=H(d_2,0)$

图19. $L_5$ 时 $L_6$ 图像

Figure 20. When $(u_{S1}^{\pm }(\xi ),v_{S1}^{\pm }(\xi ))$ , the diagram of $h>H(d_2,0)$

图20. $L_5$ 时 $L_6$ 图像

Figure 21. When $(u_{P7}^{+}(\xi ),v_{P7}^{+}(\xi ))$ , the diagram of ${\beta }^2\text{+}(\alpha -{\gamma }_1)(\alpha -{\gamma }_{\text{2}})<0$

图21. ${(\frac{{\gamma }_1+{\gamma }_2}{2})}^2<\frac{-l}{3}$ 时 $k_5^2>\frac{1}{2}$ 图像

Figure 22. When $x$ , the diagram of ${\gamma }_1,{\gamma }_2$

图22. ${\gamma }_2<d_1=\frac{-d-\sqrt{-3d^2-4l}}{2}<d_2=d<d_3=\frac{-d+\sqrt{-3d^2-4l}}{2}<{\gamma }_1$ 时 $h\to H^{+}(d_2,0)$ 图像

6. 结论

本文我们运用平面动力系统定性分析和首次积分法相结合的方法，求出了耦合KdV型方程在各种不同条件下具有的全部周期波解和孤波解，尤其是我们求出了该方程的两类新孤波解给出，以及扭状孤波解，还求出了非对称同宿轨线所围的闭轨对应的新周期波解及包围同宿轨线的闭轨对应的新周期波解。更发现了所研方程为什么能产生孤波解和周期波解，实际上是该方程解的振幅对应的Hamilton系统的能量变化起着关键的作用，本文的方法是非常有意义的。此外，由于当 ${\gamma }_2\to -d_2-\sqrt{-2l-2d_2^2},{\gamma }_1\to -d_2+\sqrt{-2l-2d_2^2},$ 时耦合KdV型方程即化为组合KdV方程，从本文结果易推得组合KdV方程的相应结论，限于篇幅，本文省略。

NOTES

$L_5$

^*通讯作者。