中高纬度地区GPS/GLONASS/BDS-3组合精密相对定位性能评估

Performance Evaluation of the Combined GPS/GLONASS/BDS-3 Precision Relative Positioning in Middle and High Latitudes

摘要: 目前，短基线定位的研究大都基于低纬度和中纬度地区，并且基于GPS、Galileo和BDS的研究占极大比例，由于GLONASS模糊度的特殊性，涉及中高纬度地区关于GLONASS的短基线定位研究较少。为了研究中高纬度地区GPS/GLONASS/BDS-3的定位效果，通过对GLONASS的模糊度进行重组的方法并设置不同高度角模拟不同遮挡情况下对单系统以及不同组合系统的模糊度固定率、模糊度成功率、可视卫星数以及定位精度等方面进行对比分析。结果显示，在15˚截止高度角下进行单频单历元基线解算模糊度固定率处于最为理想状态达到95%以上，模糊度成功率达到90%以上。总体上，在中高纬度地区，GPS/ GLONASS/BDS-3组合定位精度可达到cm级。

Abstract: At present, most of the research on short-baseline positioning is based on low-latitude and mid-latitude regions, and the research based on GPS, Galileo and BDS accounts for a large propor-tion. Due to the particularity of GLONASS ambiguity, there are few short-baseline positioning re-searches on GLONASS in mid-latitude and high-latitude regions. In order to study the positioning effect of GPS/GLONASS/BDS-3 in middle and high latitudes, through the method of reorganizing the ambiguity of GLONASS and setting different altitude angles to simulate different occlusion situa-tions, the ambiguity fixation rate, ambiguity success rate, number of visible satellites, and position-ing accuracy of a single system and different combined systems are compared and analyzed. The results show that the ambiguity fixation rate of the single-frequency single-epoch baseline solution is in the most ideal state, reaching more than 95%, and the ambiguity success rate reaches more than 90%. In general, in the middle and high latitudes, the combined positioning accuracy of GPS/GLONASS/BDS-3 can reach cm-level.

1. 引言

目前，随着全球导航定位系统的发展和建设，GNSS正朝多频多系统的方向发展 [1] [2] 。2020年6月23日我国北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)最后一颗卫星发射，标志着我国北斗全面组网成功。与其它卫星导航定位系统不同，BDS-3不仅具备定位、导航、授时功能，其还有其它卫星导航系统不具备的短报文通信服务能力 [3] [4] [5] [6] 。随着我国北斗导航系统的建成BDS-3已经广泛应用到各个领域中。

在单个卫星导航系统卫星定位精度不佳的情况下主要采取多系统组合定位改善这一情况，目前国内外对导航定位的研究主要集中在BDS及其与GPS组合的载波相对定位并主要集中在低纬度地区，而对中高纬度地区下的GPS/GLONASS/BDS-3三系统组合定位的研究较少，尤其是在卫星信号高遮挡情况下的研究较少。由于GLONASS采用FDMA技术与其它卫星导航系统不同，其不同卫星的载波频点不同， 所以GLONASS模糊度解算以及与其它导航系统实现组合定位更为复杂 [7] [8] ，因此对单独地使用GLONASS定位或者基于GLONASS与其它卫星导航定位的研究较少。文献 [7] 采集北京地区不同长度基线主要针对基于BDS-2的位于中纬度地区GPS/GLONASS/BDS研究，介绍了不同系统组合下的定位精度，其实验表明14 km基线平面和垂直定位精度可达3.01 cm和4.71 cm。文献 [9] 主要针对基于BDS-2的中纬度地区GPS/GLONASS/BDS的单点定位，但没有涉及基于BDS-3的中高纬度地区的GPS/GLONASS/BDS-3组合精密定位。针对上述情况，本文利用两组不同长度的基线(约4.47 km与约8.65 km)采用GLONASS模糊度重组法并模拟不同信号遮挡环境研究在中高纬度地区下GPS/GLONASS/BDS-3组合精密相对定位性能来对基于BDS-3的中高纬度地区的定位效果提供参考。

2. 坐标与时间系统的统一

由于采用的时间基准与空间基准不同，GLONASS坐标系统与ITRF2000差异只在原点平移，在X、Y、Z方向分别为：−0.36 m、+0.08 m、+0.18 m [8] 。WGS-84与ITRF2000差异可以忽略，三者之间换算关系为 [9]

$\{\begin{array}{l}\text{GPST}=\text{UTC}\left(\text{USNO}\right)+1\text{s}\times n-19\text{s}\\ \text{BDT}=\text{UTC}\left(\text{NTSC}\right)+1\text{s}\times n-19\text{s}-14\text{s}\\ \text{GLONASS}=\text{UTC}\left(\text{SU}\right)+3\text{h}-{\tau }_r\end{array}$ (1)

式中，n代表国际原子时(AIT)与UTC之间需要持续调整的参数， ${\tau }_r$ 为GLONASS与UTC (SU)之间存在的1 ms内系统偏差。本文在数据处理时选择GPST作为统一的时间基准，具体的转换关系为 [9]

$\{\begin{array}{l}\text{GPST}=\text{BDT}+14\text{s}+{\tau }_{\text{UTC}\left(\text{USNO}\right)-\text{UTC}\left(\text{NTSC}\right)}\\ \text{GPST}=\text{GLONASST}-3\text{h}+{\tau }_r+1\text{s}\times n-19\text{s}+{\tau }_{\text{UTC}\left(\text{USNO}\right)-\text{UTC}\left(\text{SU}\right)}\end{array}$ (2)

完成BDT，GLONASST与GPST之间的整数秒转换关系后，BDT，GLONASS与GPST之间还分别存在关于时间的系统间偏差；在实际定位解算中，上述系统间偏差不影响相对定位 [10] ，这是因为双差过程中消除了钟差参数。

3. GPS/GLONASS/BDS-3基线处理模型

3.1. 函数模型

多系统组合基线解算方式采用伪距以及载波相位观测值双差组合实现相对定位。其中GPS、BDS-3双差载波相位和伪距观测方程表达式可用式(3)表示；GLONASS双差载波相位和伪距观测方程表达式可用式(4)表示

$\{\begin{array}{l}\nabla \Delta {\varphi }_{kl}^{ij}=\nabla \Delta {\rho }_{kl}^{ij}+\lambda N_{kl}^{ij}-\nabla \Delta I_{kl}^{ij}+\nabla \Delta T_{kl}^{ij}+{\epsilon }_{kl}^{ij}\hfill \\ \nabla \Delta P_{kl}^{ij}=\nabla \Delta {\rho }_{kl}^{ij}-\nabla \Delta I_{kl}^{ij}+\nabla \Delta T_{kl}^{ij}+e_{kl}^{ij}\hfill \end{array}$ (3)

$\{\begin{array}{l}\nabla \Delta {\varphi }_{kl}^{ij}=\nabla \Delta {\rho }_{kl}^{ij}+\left({\lambda }^j{N}_{kl}^j-{\lambda }^i{N}_{kl}^i\right)-\nabla \Delta I_{kl}^{ij}+\nabla \Delta T_{kl}^{ij}+{\epsilon }_{kl}^{ij}\hfill \\ \nabla \Delta P_{kl}^{ij}=\nabla \Delta {\rho }_{kl}^{ij}-\nabla \Delta I_{kl}^{ij}+\nabla \Delta T_{kl}^{ij}+e_{kl}^{ij}\hfill \end{array}$ (4)

式中， $\nabla \Delta {\varphi }_{kl}^{ij}$ 为载波双差相位观测值，其中， $\nabla \Delta$ 为双差算子，k、l分别为参考站与流动站，i、j分别为参考星与非参考星； $\lambda$ 为信号的载波波长；N表示载波相位观测中的未知整周模糊度； $\nabla \Delta {\varphi }_{kl}^{ij}$ 为载波双差相位观测值； $\nabla \Delta {\rho }_{kl}^{ij}$ 为卫星至接收机的双差几何距离； $N_{kl}^{ij}$ 为双差整周模糊度，具有整数特性 [11] ； $\nabla \Delta I_{kl}^{ij}$ 为双差电离层延迟； $\nabla \Delta T_{kl}^{ij}$ 为双差对流层延迟； ${\epsilon }_{kl}^{ij}$ 、 $e_{kl}^{ij}$ 分别为载波与伪距双差观测值噪声。

由(3)式和(4)式可知，双差过程中消除了大部分误差影响，其中包括卫星钟差、接收机钟差、卫星星历误差、对流层和电离层延迟误差。由于GLONASS不同卫星采用不同的频率，接收机钟差无法消除，其双差模糊度不具有整周特性，所以GLONASS双差观测值的模糊度处理较为复杂 [12] 。以上是系统内差分过程，也可以选择系统间差分，缺点是系统间差分时，如果系统间系统误差不能处理好，会影响定位结果的精度 [13] ；需要注意的是由于GLONASS的两颗卫星载波波长 ${\lambda }_i$ 和 ${\lambda }_j$ 并不相同，模糊度在双差观测方程中的表现形式与GPS或BDS-3差异较大，故式(4)中的GLONASS双差模糊度项 $\left({\lambda }_j{N}_l^j-{\lambda }_i{N}_k^i\right)$ 不再具有整数特性，因此进行如下变换 [12] [14] ：

$\begin{array}{c}{\lambda }^j{N}_{kl}^j-{\lambda }^i{N}_{kl}^i={\lambda }^j{N}_{kl}^j-{\lambda }^j{N}_{kl}^i+{\lambda }^j{N}_{kl}^i-{\lambda }^i{N}_{kl}^i\\ ={\lambda }^j{N}_{kl}^{ij}+\left({\lambda }^j-{\lambda }^i\right)N_{kl}^i\end{array}$ (5)

经上述变换，双差模糊度被分解为具有整周特性的双差模糊度项 ${\lambda }^j{N}_{kl}^{ij}$ 和单差模糊度项 $\left({\lambda }^j-{\lambda }^i\right)N_{kl}^i$ ，对于单差模糊度 $N_{kl}^i$ ，可按下式进行估算 [14] [15] ：

$N_{kl}^i=\left(P_{kl}^i-{\lambda }^i{\varphi }_{kl}^i\right)/{\lambda }^i$ (6)

所以，解算GLONASS的模糊度时，双差模糊度是根据单差模糊度固定的，之后重新计算单差模糊度。

3.2. 随机模型

采用高度角随机模型进行数据处理，其函数模型以运行中的卫星高度角为变量对观测值的方差进行估计，即 [16] [17] [18] ：

${\sigma }^2=f\left(Elev\right)$ (7)

式中， $\sigma$ 为观测值中误差； $ELev$ 为卫星的高度角，这些函数模型中其中最常用的为正弦函数模型，为了更好的定义低高度角情况下的观测值的中误差，常常采用改进的正弦函数模型，即 [19] ：

${\sigma }^2=a^2+b^2/{\left(\sin \left(Elev\right)\right)}^2$ (8)

式中，a和b一般都是经验值，常取 $a=4\text{mm}$ ， $b=3\text{mm}$ 。

GNSS定位精度效果受随机模型的直接影响，忽略单系统不同系统间观测值的相关性组合系统双差观测值的方差–协方差阵为：

$D_{\text{C/G/R}}=\left(\begin{array}{ccc}{D}_{\text{BDS-3}}& & \\ & D_{\text{GPS}}& \\ & & D_{\text{GLONASS}}\end{array}\right)$ (9)

式中， $D_{\text{BDS-3}}$ ， $D_{\text{GPS}}$ ， $D_{\text{GLONASS}}$ 以及 $D_{\text{C/G/R}}$ 分别是BDS-3，GPS，GLONASS以及三系统组合双差观测值的方差–协方差矩阵。

根据误差传播定律，各系统双差观测值的方差–协方差矩阵为 [20] ：

$D_{(\cdot )}=a^{2}A+b^2{B}_{el}$ (10)

式中， $B_{el}={\left[\begin{array}{cccc}{f^2\left(el\right)|}_{kl}^i& {f^2\left(el\right)|}_{kl}^i& \cdots & {f^2\left(el\right)|}_{kl}^i\\ {f^2\left(el\right)|}_{kl}^i& {f^2\left(el\right)|}_{kl}^i& \cdots & {f^2\left(el\right)|}_{kl}^i\\ ⋮& ⋮& \ddots & ⋮\\ {f^2\left(el\right)|}_{kl}^i& {f^2\left(el\right)|}_{kl}^i& \cdots & {f^2\left(el\right)|}_{kl}^i\end{array}\right]}_{m\times m}$ ， $A={\left[\begin{array}{cccc}4& 2& \cdots & 2\\ 2& 4& \cdots & 2\\ ⋮& ⋮& \ddots & ⋮\\ 2& 2& \cdots & 4\end{array}\right]}_{m\times m}$ ；其中，a，b为常数项因子， $f\left(el\right)$ 为与高度角el相关的函数； ${f^2\left(el\right)|}_{kl}^i={f^2\left(el\right)|}_k^i+{f^2\left(el\right)|}_l^i$ ， ${f^2\left(el\right)|}_{kl}^{ij}={f^2\left(el\right)|}_k^i+{f^2\left(el\right)|}_k^j+{f^2\left(el\right)|}_l^i+{f^2\left(el\right)|}_l^j$ ， $\left(j=1,2,\cdots ,m\right)$ ，i为参考星，m为非参考星数。

4. 实验分析及处理策略

4.1. 实验数据及基线处理策略

为评估GPS/GLONASS/BDS-3短基线在中高纬度地区的定位性能与可靠性，本文选取了IGS中心4个位于北半球的测站分别为HUEG、BRMG、KIR0、KIRU，数据信息见表1，采集日期从2021-07-29至2021-08-04共7天，数据采样间隔为30 s。其中HUEG和BRMG组成基线A，KIR0和KIRU组成基线B。

本实验采用事后处理方式获得的坐标作为参考值，数据处理策略采用最小二乘进行参数估计，逐历元计算模糊度浮点解，然后采用LAMBDA法尝试模糊度固定 [21] ，固定效果可以根据两个方面进行综合评价，分别是模糊度固定率以及模糊度成功率 [22] [23] [24] [25] ，并用Ratio阈值进行检验，Ratio阈值设为2或3的情况下较多，通常情况下设为3。分别对设置的不同高度角处理模式进行实验统计与分析。

4.2. 不同高度角卫星可见数及各测站信噪比分析

卫星可见性是在特定仰角下地面某点在某时刻能观测到的所有卫星的数量或某时段所有观测卫星的跟踪弧段长度 [26] ，分析其可见性能够从测站位置的角度了解、评价系统卫星的运行情况 [27] 。通过对单系统及其组合系统观测数据的处理，利用不同截止高度角对不同遮挡情况进行模拟 [28] ，对截止高度角10˚、15˚、30˚、45˚时GPS、GLONASS与BDS-3的可观测卫星数量进行统计，结果如图1所示。从图1中可以看出，当截止高度角为小于等于15˚时，在观测时段内平均可观测卫星数在4颗以上满足信号遮挡情况下的定位要求；当截止高度角为30˚时，在观测时段内平均可观测卫星数为4.4颗，BDS-3系统出现了大量历元卫星数不足4颗的情况；当截止高度角为45˚时，GLONASS和BDS-3单系统出现了可观测卫星数不足4颗的历元，此时不满足定位要求。

通常用信噪比(Signal-to-Noise Ratio, SNR)反映GNSS载波信号质量的优劣，其数值大小代表着观测信号的质量 [29] [30] 。信噪比通常以dB/Hz为单位 [31] ，其表达式如下：

$\text{SNR}=P_R/\left(kT{B}_n\right)$ (11)

式中： $B_n$ 为噪声带宽(Hz)；k为波尔曼常数，为1.38 × 10⁻²³ J/K。

为了分析北斗三新频点B1C的信噪比情况，图2给出了四个测站北斗三B1C频点七天的信噪比统计结果，从图中可以看出四个测站的B1C平均信噪比均大于40 dBHz。

Table 1. Summary of experimental data

表1. 实验数据概况

(a) (b)

Figure 1. Number of visible satellites for baselines (a) (left) and (b) (right) at elevation cutoff angles of 10˚, 15˚, 30˚ and 45˚

图1. 基线(a) (左)和(b) (右) 10˚、15˚、30˚和45˚截止高度角的可视卫星数

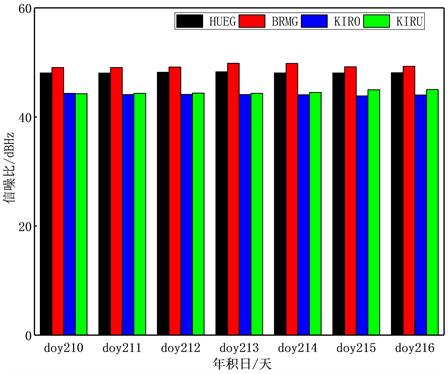
Figure 2. The mean value of the signal-to-noise ratio of the B1C signal at each station

图2. 各测站B1C信号信噪比均值

4.3. 模糊度解算结果分析

模糊度解算性能是影响载波相位相对定位精度的主要因素 [7] ，表2给出了七天数据实验统计结果的平均值，限于文章篇幅表中只给出部分实验模糊度解算性能对比，固定率检验以设定Ratio阈值的方法来确定。其中，模糊度固定率与成功率分别定义如下：

$\{\begin{array}{l}固定率=\frac{满足阈值的历元数}{总有效历元数}\\ 成功率=\frac{正确固定历元数}{总有效历元数}\end{array}$ (12)

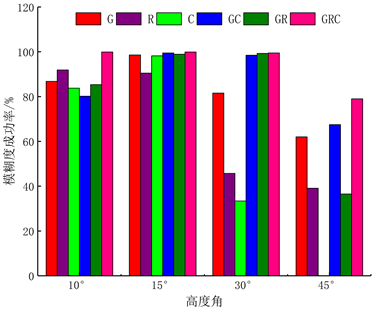
在进行解算过程中，可能出现错误符合Ratio阈值模糊度组 [23] 。由表2和图3可以看出，对于8.652 km长的基线A，在10˚和15˚的卫星截止高度角情况下，GPS、GLONASS和BDS-3在模糊度固定率与成功率相当；截止高度角为30˚和45˚时，单系统下GPS模糊度固定率和成功率最高，GLONASS的成功率也低于50%，BDS-3固定效果较差，结合图1可知，这是由于GPS在可见性上要优于GLONASS和BDS-3。单系统固定率与成功率随着高度角的增加都呈现出下降趋势，但GPS/BDS-3与GPS/GLONASS/BDS-3的固定率与成功率都高于75%。对于基线B，截止高度角为10˚和15˚时，BDS-3成功率超过了80%，GPS和GLONASS超过了90%，而GPS与其它系统组成的组合系统成功率高达95%以上；截止高度角为30˚时，BDS-3可视卫星数减少使得其固定率与成功率大幅下降，而GPS/BDS-3、GPS/GLONASS与GPS/GLONASS/BDS-3固定率与成功率依然高达95%以上，对于45˚截止高度角的不利观测条件下GPS与GLONASS的模糊度固定率与多系统组合的模糊度固定率基本相当，BDS-3固定效果较差，单系统固定成功率远低于多系统。

4.4. 基线向量定位结果分析

本文利用基线偏差进行精度分析，将正确固定的历元的解算结果与参考值做差。限于篇幅，以10˚截止高度角为例图4给出了两条基线的解算结果，表3给出了在单历元模式下单系统及不同系统组合情况下的相对定位的内符合精度。

Table 2. Statistics on ambiguity fixation of single system and different combined systems

表2. 单系统及不同组合系统模糊度固定情况统计

(a) (b)

Figure 3. Ambiguity success rates for Baseline (a) (left) and Baseline (b) (right) at elevation angles of 10˚, 15˚, 30˚, and 45˚

图3. 基线(a) (左)和基线(b) (右)在10˚、15˚、30˚和45˚高度角下的模糊度成功率

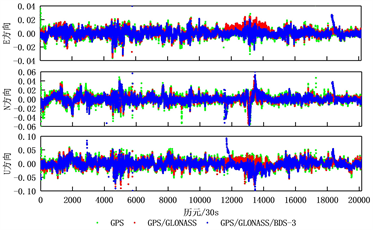
从图4和表3可以得出，对于8.652 km长的基线A，截止高度角为10˚~30˚时，GPS、GLONASS和BDS-3单系统的定位精度都在cm级，而在GPS/GLONASS/BDS-3组合系统下平面定位精度可达mm级；当卫星截止高度角为45˚时单个系统定位效果不理想，其中BDS-3定位效果不及GPS和GLONASS。对于4.472 km长的基线B，截止高度角为10˚、15˚和30˚时GPS定位精度可达cm级，优于GLONASS和BDS-3定位精度，三系统组合平面定位精度可达mm级；当卫星截止高度角为45˚时，GPS、GLONASS和BDS-3定位效果不理想，GPS和GLONASS定位精度达到分米级，组合系统在E、N、U方向定位精度优于单系统。4.472 km短基线B与8.652 km基线A相比，定位精度效果较为理想。

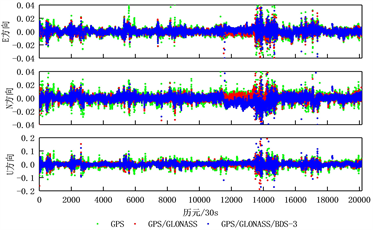(a) (b)

Figure 4. Deviations of GPS, GPS/GLONASS and GPS/GLONASS/BDS-3 systems in E, N, U directions when the altitude angle is 10˚

图4. 高度角为10˚时GPS、GPS/GLONASS及GPS/GLONASS/BDS-3系统在E、N、U方向的偏差

Table 3. Statistics of fixed solution accuracy of single system and different combined systems (cm)

表3. 单系统及不同组合系统固定解精度统计(cm)

5. 结论

本文分别从可见卫星数，信噪比，定位精度等方面评估和分析了GPS/GLONASS/BDS-3在中高纬度地区的定位性能，本文利用两组数据，在不同基线长度环境下，对GPS、GLONASS、BDS-3单系统以及GPS/BDS-3、GPS/GLONASS、GPS/GLONASS/BDS-3组合系统的相对定位性能进行了分析对比，实验结果表明，多系统组合情况下的可视卫星数和系统稳定性较单系统而言有所提高。在15˚截止高度角下模糊度固定率和成功率较高，在卫星截止高度角为45˚的不利观测条件下，BDS-3模糊度固定效果不理想，多系统组合明显提高了单系统的模糊度固定成功率。从整体上来看在15˚截止高度角下进行单频单历元基线解算模糊度固定率处于最为理想状态达到95%以上，模糊度成功率达到90%以上，GPS/GLONASS/BDS-3组合的定位精度要好于单系统定位精度。因此，在中高纬度地区，GPS/GLONASS/BDS-3单频单历元定位精度可达到cm级。

参考文献