1. 引言
超声振动辅助加工是一种通过超声波产生的振动辅助机械加工的技术,它可以改善加工表面质量、提高加工精度和加工效率,并且在某些应用领域中已经得到了广泛应用。吕婷等 [1] 利用FLUENT软件模拟了超声抛光中存在的空化现象,对流场的相关参数进行了数值模拟,并对加工质量进行了预测。孙冰 [2] 对超声空化进行了数值模拟,分析流场的流体速度,气含率等,进而对超声空化发生的机理和影响因素进行了分析。Zhai等人 [3] 提出了超声振动辅助磁流变抛光工艺对蓝宝石晶片进行加工,得到了晶圆的表面质量和抛光效率受复合磨料的外壳厚度影响。刘仁鑫等人 [4] 复合了超声与化学机械抛光工艺,对硅片边缘进行抛光。通过研究超声振动的不同形式,发现了椭圆超声振动能得到最优的抛光效果。Zhou等人 [5] 研究了蓝宝石超声化学抛光的多物理场,对其进行了CFD仿真与试验分析,验证了超声空化作用对材料去除的影响。试验证明,在超声加工区域内的切削液在超声正负压相的作用下能产生有益的空化效应 [6] [7] 。
结合上述分析,对超声振动过程中的流场进行数值模拟,有助于选取合适的工件安装方式以及对材料去除机理进行更深层次的研究。本文基于计算流体动力学软件FLUENT,研究工件在不同安装方案时,对超声振动流场进行数值模拟从而对空化现象进行研究。
2. 超声抛光流场几何模型建立
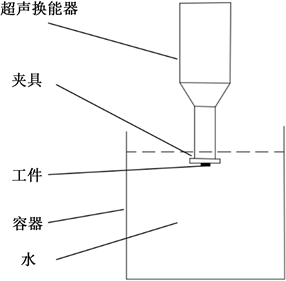
本文以超声振动下的流场作为分析对象,分为工件与超声振头固定装夹和工件单独装夹两种方案来进行研究,其试验原理图如图1所示。
 (a)
(a)  (b)
(b)
Figure 1. Clamping method of workpiece. (a) Workpiece and ultrasonic probe fixed clamping; (b) The workpiece is clamped separately
图1. 工件的装夹方式。(a) 工件与超声振头固定装夹;(b) 工件单独装夹
3. 仿真结果与分析
3.1. 模型的建立与网格的划分
根据图1工件的安装方式,为了简化计算、节约计算时间,对模型进行二维简化如图2所示。只需要在ICEM CFD中确定好节点的位置,然后将各个节点一次连接,就可以得到流场的二维模型。
 (a)
(a) 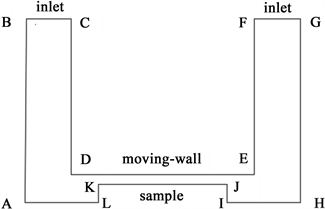 (b)
(b)
Figure 2. Simplified model of flow field. (a) Simplified model of flow field in Scheme a; (b) Simplified model of flow field in Scheme b
图2. 流场简化模型。(a) 方案a中流场简化模型;(b) 方案b中流场简化模型
绘制好的模型直接在ICEM CFD中进行网格划分,为了得到更为精确的计算结果,考虑到模型的动网格类型,对流体区域采用非结构化网格划分,网格全局尺寸设置为0.1,经网格划分后,方案a有134,996个单元,方案b有53,678个单元,其网格划分的二维模型如图3所示。
 (a)
(a)  (b)
(b)
Figure 3. Meshing results of simplified model of flow field. (a) Meshing results of Scheme a; (b) Meshing results of Scheme b
图3. 流场简化模型的网格划分结果。(a) 方案a网格划分结果;(b) 方案b网格划分结果
3.2. 仿真前处理
3.2.1. 边界条件的设置
图2流场简化模型图2(a)中AB、AH、GH为壁面,BC、FG为容器内部与外界的交界面,DE代表在超声振头上的工件。模型的详细参数以及比边界类型和边界名称如下表1所示。

Table 1. Setting of model boundary conditions in Scheme a
表1. 方案a模型边界条件设置
图2流场简化模型图2(b)中,AB、AL、IH和HG代表壁面,JK代表工件,BC和FG代表容器内部与外界的交界面。模型的详细参数以及边界类型和边界名称如下表2所示。

Table 2. Setting of model boundary conditions in Scheme b
表2. 方案b模型边界条件设置
3.2.2. 流场计算参数设置
求解器设置为transient,加入两相流混合模型,选择
模型,设置液态水为主相,水蒸气为次相,考虑两两相互作用模型选择cavitation。模拟环境为标准大气压,室温环境。设置动网格,其中动边界的位移方程为:
(1)
其中,a = 30 μm、f = 20 kHz、t为运行时间。
对上述方程求导则可得到速度方程:
(2)
3.3. 气含率仿真结果分析
本小节主要研究了流场内气含率的大小,因此仿真结果主要参考了不同时刻的气含率的大小,以及其在流场内的分布情况。方案a的气含率分别在t = 10 ms、t = 20 ms、t = 30 ms以及t = 40 ms时刻的分布情况如下图4所示。
 (a)
(a)  (b)
(b) 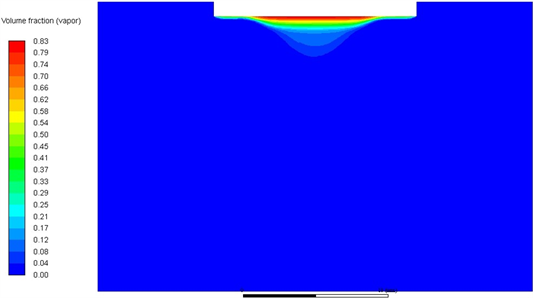 (c)
(c)  (d)
(d)
Figure 4. Distribution of vapor volume fraction in flow field at different times in Scheme a. (a) Vapor volume fraction at t = 10 ms; (b) Vapor volume fraction at t = 20 ms; (c) Vapor volume fraction at t = 30 ms; (d) Vapor volume fraction at t = 40 ms
图4. 方案a中不同时刻气含率流场内分布情况。(a) t = 10 ms时气含率分布;(b) t = 20 ms时气含率分布;(c) t = 30 ms时气含率分布;(d) t = 40 ms时气含率分布
由上述仿真结果可知,在方案a中,在动边界附近,气含率大小在t = 10~40 ms时刻总体成增大的趋势,且在t = 10~30 ms这个时间段内气含率的分布范围总体呈向下扩散的趋势,在t = 40 ms时气含率的大小到达了最大值,同时气含率的分布范围也是较为集中;并且在非振动区域内,气含率大小是为0的,因为在非振动区域内无法产生超声空化现象,因此也没有空化气泡的产生,所以气含率的大小为0,这是符合正常工况的。总体而言,气含率的分布主要集中在工件振动区间,且由该区域向下呈扩散趋势。
由图5可知,气含率在动边界的中点处达到极大值,且气含率的分布沿动边界的中点两端对称,动边界上气含率大小有着明显的波动。在t = 40 ms时气含率极大值相较于其他时刻达到了最大值0.8987。
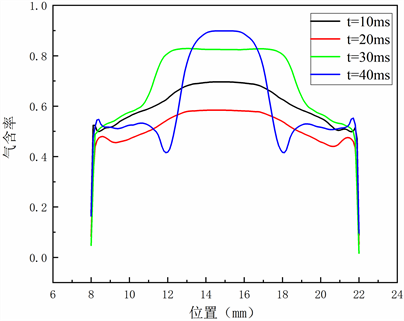
Figure 5. Vapor volume fraction at different times on moving-wall in Scheme a
图5. 方案a不同时刻动边界气含率大小
由图6可知,绝对压力在动边界处自上而下衰减,最大值达到了202,538 pa,且绝对压力的分布规律在左右两端近似对称,在动边界处绝对压力最小,最小值为3540 pa,达到了空化阈值,此时在动边界附近产生会空化效应,因此气含率主要集中分布在动边界附近。
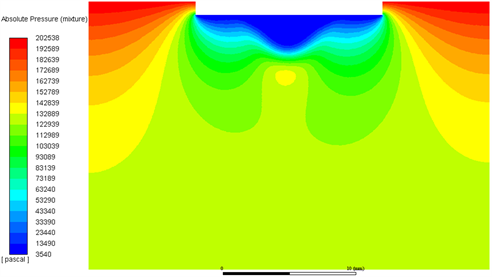
Figure 6. The absolute pressure distribution at t = 30 ms
图6. t = 30 ms时绝对压力分布
由图7可知,气含率和流场压力的峰值交替出现,这主要时由于在绝对压力较低时,流场内的空化气泡产生、膨胀因此气含率随之增加;而当绝对压力过高时,流场内原本存在的空化气泡会因此溃灭,所以气含率随之降低。
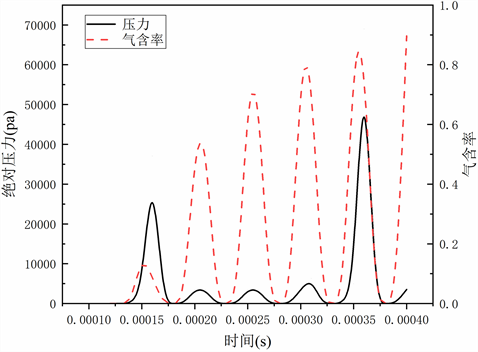
Figure 7. Vapor volume fraction and pressure at the middle point of moving-wall in Scheme a
图7. 方案a动边界中点处气含率和压力大小
方案b的气含率分别在t = 10 ms、t = 20 ms、t = 30 ms以及t = 40 ms时刻的分布情况如下图8所示。
由下述仿真结果分析可知,在动边界附近,气含率大小在t = 10~40 ms时刻呈上升趋势,在t = 40 ms时气含率的大小达到了最大值;在非振动区域,气含率在流场区域下端也出现了较少的分布,这主要是由于动边界与工件的间隔较小,而产生的气含率较大,因此会有部分空化气泡往两端向下运动,从而在该区域内也会有较小的气含率分布。总体而言,在上述时刻分析气含率数值总体较大,且气含率的分布情况总体向左右两端扩散。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 8. Distribution of vapor volume fraction in flow field at different times in Scheme b. (a) Vapor volume fraction at t = 10 ms; (b) Vapor volume fraction at t = 20 ms; (c) Vapor volume fraction at t = 30 ms; (d) Vapor volume fraction at t = 40 ms
图8. 方案b中不同时刻气含率流场内分布情况。(a) t = 10 ms时气含率分布;(b) t = 20 ms时气含率分布;(c) t = 30 ms时气含率分布;(d) t = 40 ms时气含率分布
由下图9可知,方案b的气含率在动边界两端点处达到极大值,总体上在同一时刻在动边界上的气含率数值的波动较小;在不同时刻,随着时间的增加,气含率的大小也随之增大。在t = 40 ms时气含率达到最大值为0.9598。
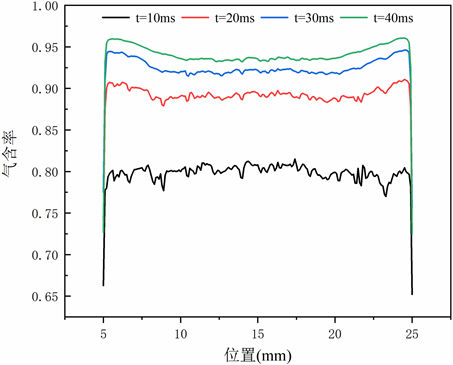
Figure 9. Vapor volume fraction at different times on moving-wall in Scheme b
图9. 方案b不同时刻动边界气含率大小
分别取方案a动边界DE的中点以及方案b动边界DE的中点为监测点,分别得到在不同时刻该点的气含率具体数值,如下表3所示。
根据下表3中监测点下方案a和方案b在不同时刻气含率大小,得到气含率的变化趋势对比如下图10所示。

Table 3. Vapor volume fraction at different times at monitoring points
表3. 监测点下不同时刻气含率的大小
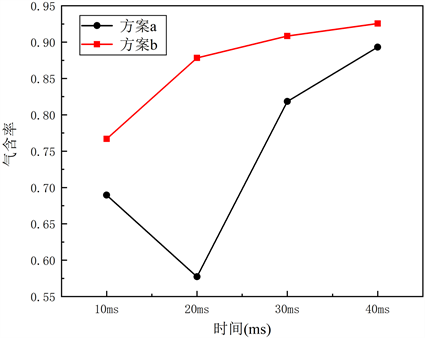
Figure 10. Vapor volume fraction trends of Scheme a and Scheme b at different times
图10. 方案a和方案b在不同时刻气含率变化趋势
由上表3和图10可知,在同一时刻方案b的气含率始终高于方案a的气含率。在t = 20 ms时,二种工件安装方案的气含率相差达到了最大幅度,与方案a相比,方案b气含率提高了52.12%,而在其余时刻,方案b的气含率始终也高于方案a的气含率,在t = 40 ms时,二种工件安装方案气含率相差达到最小,此时气含率相差3.63%。考虑到气含率主要反映的是空化气泡的密度,而空化气泡的溃灭会产生微射流对工件表面的凸峰进行去除作用,因而气含率的大小能一定程度的反映出对工件表面的加工作用,因此基于上述分析,与工件振动相比,固定工件流场的振动区间内能产生更大的气含率,从而更有助于对工件的加工。
4. 结论
本文以超声振动工件的两种安装方式为研究对象,基于ICEM CFD建立二维模型并进行网格划分,在计算流体动力学软件FLUENT中对其进行了数值模拟,结果表明,流场的主要空化区域发生在振动边界处;在不同时刻,固定工件流场的振动区域内的气含率都明显高于工件振动流场的气含率。结合由空化气泡溃灭所产生的能量对工件表面凸峰的冲击去除作用可知,方案b固定工件安装能达到更好的材料加工效果。