CO₂/N₂在不同挥发分烟煤中的吸附特性研究

Study on Adsorption Characteristics of CO₂/N₂ in Bituminous Coal with Different Volatile Contents

摘要: 为研究CO₂、N₂在不同挥发分烟煤中的吸附特性，本文对煤LL (C₁₈₆H₁₅₃NO₆)、煤PDS-1 (C₂₀₇H₁₆₅NO₁₁)和煤XZ (C₁₈₁H₁₆₃NO₆)在不同温度和不同压力下进行了巨正则蒙特卡洛模拟和分子动力学模拟。结果表明，CO₂在不同挥发分烟煤分子中的吸附量和吸附速率大于N₂吸附量，在低挥发分烟煤中极限吸附量最大，且随着挥发分程度升高而降低；两种气体的吸附热都小于40 kJ/mol，并且对于压力和温度的变化不敏感。另外，CO₂和N₂更容易吸附在含氧官能团和苯环附近。CO₂和N₂在煤中的扩散能力为N₂ > CO₂，这是由于CO₂具有更强的吸附能力。

Abstract: In order to study the adsorption characteristics of CO₂ and N₂ in bituminous coals with different volatiles, giant canonical Monte Carlo simulation and molecular dynamics simulation were performed on coal LL (C₁₈₆H₁₅₃NO₆), coal PDS-1 (C₂₀₇H₁₆₅NO₁₁) and coal XZ (C₁₈₁H₁₆₃NO₆) at different temperatures and pressures in this paper. The results show that the adsorption amount and rate of CO₂ in different volatile bituminous coal molecules are greater than that of N₂, and the limit adsorption amount of CO₂ in low-volatile bituminous coal is the largest and decreases with the increase of volatile content; the adsorption heat of the two gases are less than 40 kJ/mol and are not sensitive to changes in pressure and temperature. In addition, CO₂ and N₂ are more eas-ily adsorbed near oxygen-containing functional groups and benzene rings. The order of diffusivity of CO₂ and N₂ in coal is N₂> CO₂, which is due to the stronger adsorption capacity of CO₂.

1. 引言

煤炭是一种重要的能源，其中烟煤可用于电力、冶金等行业，是煤炭中重要的一类。我国矿井火灾时有发生，其中90%~94%的煤矿火灾是由煤炭自燃引起的 [1] 。煤炭自燃不仅对人民的生命和财产造成了损失，而且对环境造成了破坏，有诸多不利的影响。因此，从分子结构上对烟煤进行研究，并运用分子模拟的方法探究不同挥发分烟煤对气体吸附规律的影响，有利于更深入地理解气体在煤中的吸附特性，对煤矿采空区注惰性气体防灭火具有积极意义。

研究人员现已对烟煤对气体吸附进行了实验与模拟的多种研究。郭立稳等 [2] 为了研究低阶烟煤对CO气体的吸附性能及影响因素，对多种低阶烟煤在不同温度下，进行了CO等温吸附试验、煤质分析等工作。结果表明：低阶烟煤中对吸附CO产生影响的是其中的惰质组和过渡孔含量，并且CO吸附量与这些影响因素呈正相关。文虎等 [3] 通过模拟CO在5种不同温度、压力下的吸附量、吸附热变化。研究结果表明：随着温度的升高，CO在烟煤分子中饱和吸附量和吸附能力降低，并且CO分子由能量较高的优势吸附位点逐渐向相对较弱的吸附位点移动。秦兴林 [4] 测试了不同水分含量下的瓦斯吸附量，研究结果表明：烟煤瓦斯吸附量在干燥状态下最大，并且受水分含量影响；受水作用后，测试所用两种煤样瓦斯吸附量呈现不同的趋势，在不同水分含量情况下发现，WZ3煤样较WZ15煤样有更好的吸附性。王吉军等 [5] 采用差示扫描量热仪测定不同变质程度煤的吸热–放热曲线。结果表明：随着温度的升高，吸附N₂放出的热量随着温度的升高逐渐减小。张晓光 [6] 模拟了对CO₂和CH₄在褐煤中的竞争吸附行为，结果表明：单组分吸附时，CO₂和CH₄的吸附量大小关系为CO₂ > CH₄；而双组分吸附时，CO₂与CH₄发生竞争吸附，CH₄受到竞争吸附的影响，吸附量减少。李树刚等 [7] 模拟了不同温度下煤分子模型中CO₂、N₂、CH₄多组分气体等比例的吸附行为。结果表明：CO₂、N₂、CH₄ 3种气体在晶胞内呈现不同的吸附状态，分别为簇状分布、带状分布和点状分布；另外，3种气体的吸附量、吸附热关系为CO₂ > CH₄ > N₂，吸附势能CO₂ < CH₄ < N₂。

基于以上研究背景，本文对CO₂与N₂在不同挥发分烟煤中的吸附特性进行了研究。选取合适的烟煤分子模型，通过数值模拟方法，运用Materials Studio软件对比CO₂和N₂在两种煤分子模型中的吸附和扩散行为，为后续研究提供参考。

2. 计算方法

2.1. 煤模型的选取与构建

三种不同挥发分烟煤分别为低挥发分烟煤LL (C₁₈₆H₁₅₃NO₆)、中挥发分烟煤PDS-1 (C₂₀₇H₁₆₅NO₁₁)和高挥发分烟煤XZ (C₁₈₁H₁₆₃NO₆) [8] 。其中，低挥发分烟煤LL芳香尺寸最大，芳香单元主要以2环和3环为主；中挥发分烟煤PDS-1芳香尺寸较小，芳香单元主要是以2环和3环为主；高挥发分烟煤XZ芳香尺寸小，芳香单元主要是以苯环为主。三种不同挥发分烟煤的基本单元分别如图1所示。

Figure 1. Basic unit of coal molecule

图1. 煤分子基本单元

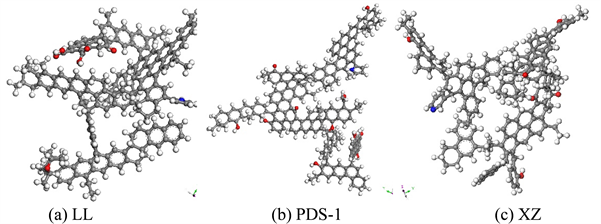
Figure 2. Structure model of coal molecules after structural optimization

图2. 结构优化后的煤分子结构模型

利用Materials Studio 2019软件中的Forcite模块对平面煤分子模型进行优化，使不同挥发分的烟煤模型能量达到稳定状态。采用Dreiding立场对煤分子进行几何优化和能量优化。运用电荷平衡法(QEq)计算电荷分布并用原子态计算静电能和范德华能。利用Anneal进行退火动力学计算能量最优状态，初始温度为300 k，最高温度为600 k。经过几何优化和退火后的煤分子基本结构能量变化如表1所示，基本结构单元如图2所示。

通过Amorphous Cell模块分别构建不同挥发分烟煤的表面模型，将优化后的煤分子模型分别填充到三维周期性边界晶胞中得到初始煤表面模型，煤LL晶胞大小为a = b = c = 15.3 Å；煤PDS-1晶胞大小为a = b = c = 15.7 Å；煤PDS-1晶胞大小为a = b = c = 14.8 Å。通过测试分别得出三种不同挥发分由低到高的烟煤密度：1.15 g/cm³、1.20 g/cm³、1.25 g/cm³。实际烟煤的密度约为1.25~1.4 g/cm³，这是由于实际烟煤含小分子以及其他元素 [9] 。煤分子表面模型结构如图3所示，其中原子颜色C：灰色，H：白色，O：红色，N：蓝色，S：黄色。

Table 1. Comparison of minimum potential energy composition energies of coal molecules

表1. 煤分子最小势能组成能量对比

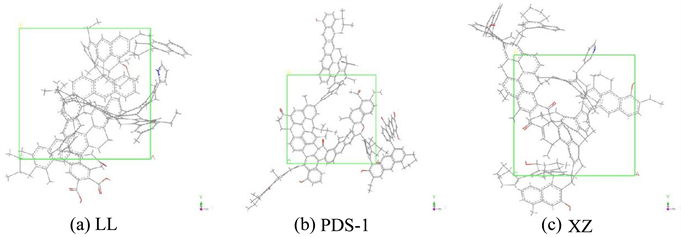
Figure 3. Structure model of coal molecules

图3. 煤分子结构模型

2.2. 蒙特卡洛模拟

蒙特卡洛(Monte Carlo)方法，属于统计试验的一种方法，主要通过进行统计抽样实验来解决各种实际问题。在分子模拟中，蒙特卡洛方法主要通过Metropolis取样在体系中产生Markov链，进而完成统计抽样实验，得出实验数据。

采用巨正则系综蒙特卡洛模拟方法计算吸附量与吸附热，在Materials Studio 2019软件中吸附模块的Fixed Pressure Task进行。在Fixed Pressure Task任务中设置温度303.15、313.15和323.15，压力范围选取0~5 MPa。选取COMPASS Ⅱ力场，静电作用与范德华相互作用分别采用Ewald加和法和Atom Based法。CO₂和N₂的摩尔质量、临界温度、临界压力和偏心因子等参数如表1所示，压力和逸度的换算由Peng-Robinson公式实现 [10] [11] 。通过Langmuir公式获得了不同温度条件下各组分气体的吸附等温线 [12] [13] 。Langmuir公式为：

$\text{y}=\frac{abx}{1+bx}$ (1)

式中：a是压力趋于无穷大时的极限吸附量，mmol/g；b是吸附常数，MPa⁻¹。根据模拟结果得出的吸附量N单位为(average molecules/cell)，通过下述等式将其转换为(mmol/g)：

$N=1000\frac{N_{am}}{N_a\cdot M_s}$ (2)

式中：N表示吸附量，mmol/g；N_am表示分子个数；N_a表示晶胞个数；M_s为单个晶胞的分子量。

Table 2. Physical properties of CO2 and N2

表2. CO₂与N₂的物理性质

吸附位置的定位在吸附模块中的Locate进行并在图像上显示。Locate中力场参数等设置与Fixed Pressure Task中的设置相同。

2.3. 分子动力学模拟

采用蒙特卡洛方法，在Adsorption Locator模块中分别让三种不同挥发分烟煤分子表面模型吸附CO₂分子和N₂分子。选择能量最低的吸附构型通过Dynamics项进行分子动力学模拟，模拟时间为100 ps，时间步长为1.0 fs。采用NVT正则系综，温度控制采用Nose方法，设为303.15 K。范德华相互作用采用Ewald求和方法，精度为10~3 kcal/mol。选取20~80 ps的数据研究体系的动力学性质。

均方位移(MSD)表示分子的平均运动和，MSD可以通过分子动力学模拟得到，其公式如(3)所示 [14] ：

$MSD=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left[r_i\left(t\right)-r_t\left(0\right)\right]}^2}$ (3)

扩散系数指分子均方位移随时间的变化率 [10] ，可以由式(4)得出：

$D=\underset{t\to \infty }{\lim }\frac{d}{6Ndt}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left[r_i\left(t\right)-r_i\left(0\right)\right]}^2}$ (4)

式中：N是粒子数，ri(t)和ri(0)分别是分子i在时间t和0的位置向量。

3. 结果与讨论

3.1. 压力与逸度的关系

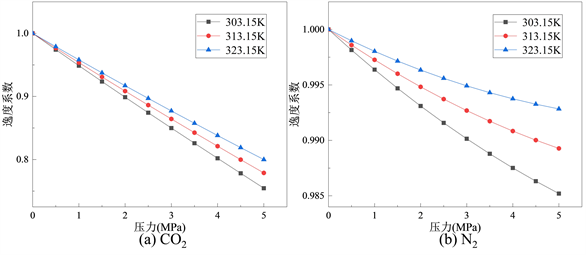
Figure 4. Relationship between gas fugacity coefficient and pressure at different temperatures

图4. 不同温度下气体逸度系数与压力之间的关系

气体逸度系数与压力的关系如图4所示。结果表明：在温度一定的情况下，随着压力增高，气体逸度系数会不断减小，而在压力恒定时，气体逸度系数会因为温度的增高而增大。根据表2所示，可知CO₂的临界温度为304.13 K，临界压力为7.38 Pa。因此，在温度为303.15~313.15 K和压力0~5 MPa的区间内没有发生梯度变化。在0~5 MPa之间，CO₂的逸度系数从0.75增加到1.00，N₂的逸度系数从0.985增加到1.00。可以发现，CO₂的逸度系数的变化率始终大于N₂，表明两种气体中CO₂的逸度系数相较于N₂的逸度系数更易受到压力的影响。

3.2. 等温吸附曲线

图5、图6和图7分别为CO₂和N₂吸附在不同挥发分烟煤的等温吸附曲线，可以发现，在相同的温度和压力下，两种气体吸附量大小顺序为：CO₂ > N₂。从单一挥发分烟煤吸附气体的吸附量可以发现，煤吸附CO₂分子的吸附量始终大于N₂分子的吸附量，可以认为烟煤的挥发分程度高低不会影响CO₂较N₂更强的吸附效能。从不同挥发分烟煤吸附气体的吸附量可以发现：对于CO₂，随着烟煤挥发分程度越来越高，CO₂的极限吸附量逐渐减小；对于N₂，低挥发分烟煤分子LL吸附量要大于中挥发分烟煤PDS-1和高挥发分烟煤XZ。

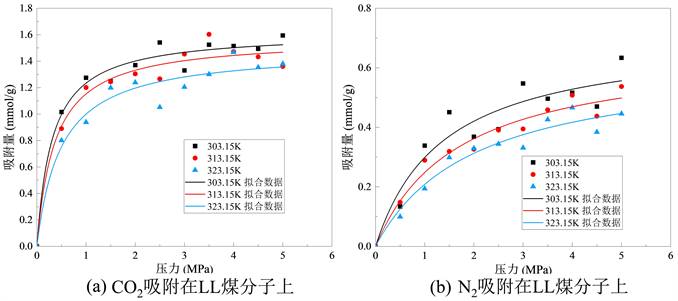
Figure 5. Isothermal adsorption curves of LL coal molecular structure on gases

图5. LL煤分子结构对气体的等温吸附曲线

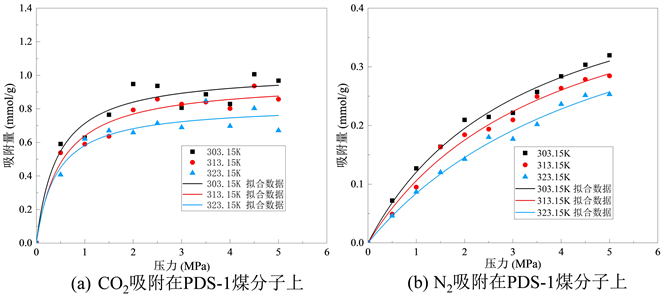
Figure 6. Isothermal adsorption curves of PDS-1 coal molecular structure on gases

图6. PDS-1煤分子结构对气体的等温吸附曲线

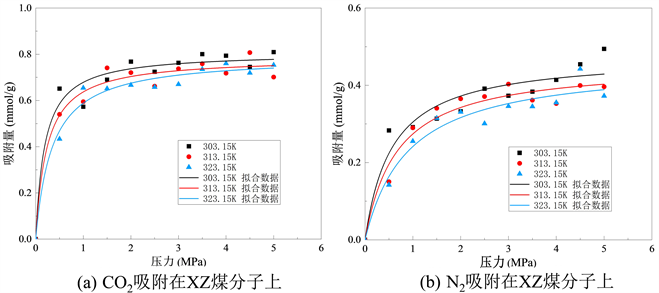
Figure 7. Isothermal adsorption curves of XZ coal molecular structure on gases

图7. XZ煤分子结构对气体的等温吸附曲线

从图中可以看出，一定温度下，随着压力增加，煤对CO₂分子吸附量逐渐增加，但吸附速率随着压力增大不断降低，当压力增大到一定值时(4~5 Mpa)，吸附量达到饱和。此外，煤对CO₂气体的吸附量受温度影响，在压力一定的情况下，随着温度升高，煤对CO₂气体的饱和吸附呈现下降趋势，对比饱和状态下(4.5 Mpa)温度不断升高，不同挥发分烟煤由低到高对CO₂吸附量分别为1.380~1.594 mmol/g、0.671~0.967 mmol/g和0.753~0.809 mmol/g。N₂与CO₂的等温吸附曲线类似，随着压力增加煤对N₂分子吸附量逐渐增加，并且吸附速率逐渐放缓，但由于CO₂更容易到达极限吸附量，故N₂分子吸附速率只有在高挥发分烟煤XZ中表现出明显的放缓。三种不同挥发分烟煤由低到高对N₂的吸附量分别为0.455~0.633 mmol/g、0.219~0.253 mmol/g和0.372~0.494 mmol/g。由不同挥发分烟煤对CO₂和N₂两种分子的吸附量和等温吸附曲线可以看出，温度升高不利于煤吸附气体。

Table 3. Langmuir fitting parameters for adsorption isotherms of coal LL at different temperatures

表3. 煤LL在不同温度下吸附等温线的Langmuir拟合参数

Table 4. Langmuir fitting parameters for adsorption isotherms of coal PDS-1 at different temperatures

表4. 煤PDS-1在不同温度下吸附等温线的Langmuir拟合参数

Table 5. Langmuir fitting parameters for adsorption isotherms of coal XZ at different temperatures

表5. 煤XZ在不同温度下吸附等温线的Langmuir拟合参数

不同挥发分烟煤在不同温度下的吸附等温线的Langmuir拟合参数分别如表3、表4和表5所示。其中，参数a和b来自等式(1)，a是压力趋于无穷大时的极限吸附容量，而b是吸附常数，与吸附能量有关。Langmuir拟合度较高，说明吸附量数据是合理的。根据上表可知，在煤LL中CO₂的a值范围为1.48~1.61 mmol/g，N₂的a值范围为2.03~3.20 mmol/g；在煤PDS-1中CO₂的a值范围为0.82~1.02 mmol/g，N₂的a值范围为0.47~0.51 mmol/g；在煤XZ中CO₂的a值范围为0.76~0.81 mmol/g，N₂的a值范围为0.43~0.47 mmol/g。比较表3、表4和表5发现，不同挥发分烟煤由低到高中CO₂的a值依次减小，表明CO₂在低挥发分烟煤中气体的极限吸附量要更大，并随着挥发分程度升高而降低；同样，N₂也存在相同的趋势，伴随着烟煤的挥发分程度升高，N₂的极限吸附量逐渐降低。该结果与图5所示的吸附量结果一致。根据表2所示，临界温度越高，吸附容量越大。吸附容量的大小顺序为CO₂ > N₂。由于CO₂的临界温度大于N₂的临界温度，因此CO₂相较于N₂可以更快地达到极限吸附容量。

3.3. 等量吸附热

CO₂与N₂分别在不同挥发分烟煤中的等量吸附热如图8所示。可以发现，在303.15 K~323.15 K的温度区间CO₂与N₂两种气体的等量吸附热并没有明显变化，说明温度由303.15 K升高至323.15 K的过程中不会影响煤吸附两种气体；同时，压力在0~5 MPa时气体的吸附热也没有明显变化。从图8可以看出，在相同的温度下，两种气体在不同挥发分烟煤的吸附热大小均为CO₂ > N₂。说明烟煤的挥发分程度不会有影响烟煤吸附气体的能力，三种不同挥发分的烟煤对于CO₂和N₂两种气体的吸附能力相同。

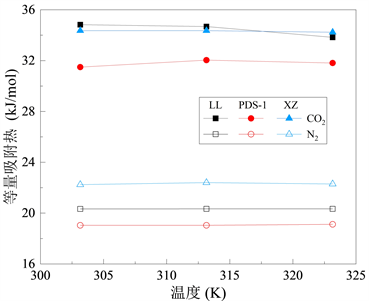
Figure 8. Relationship between the equal adsorption heat and temperature

图8. 等量吸附热与温度的关系

气体的吸附能力可以用吸附热进行衡量。物理吸附的吸附热一般为几百到几千焦耳每摩尔，最大不超过40 kJ/mol。化学吸附过程的吸附热比物理吸附过程的大，一般为84~417 kJ/mol。如表6所示，CO₂的吸附热在31.8~34.4 kJ/mol，N₂的吸附热在19.1~22.3 kJ/mol。两种气体的吸附热都小于40 kJ/mol。表明两种气体在不同挥发分烟煤中的吸附为物理吸附。

Table 6. Adsorption heat data

表6. 吸附热数据

3.4. 扩散系数

图9中(a)、(b)和(c)分别为CO₂和N₂气体在不同挥发分烟煤中的MSD曲线及线性拟合曲线。其中，根据拟合线性方程分别得到CO₂在LL、PDS-1和XZ中的斜率为0.0195、0.0530和0.0140；N₂在无烟煤和烟煤的斜率为0.0476、0.0924和0.0792。将其分别带入到式(4)中，得出CO₂在不同挥发分烟煤的扩散系数分别为3.256 × 10⁻¹¹ m²/s、8.840 × 10⁻¹¹ m²/s和2.333 × 10⁻¹¹ m²/s；N₂在不同挥发分煤的扩散系数分别为7.935 × 10⁻¹¹m²/s、1.541 × 10⁻¹⁰ m²/s和1.321 × 10⁻¹⁰ m²/s。通过比较发现，在不同挥发分烟煤中，两种气体的扩散系数都有所变化，这是由于在不同挥发分烟煤中的孔隙结构与含氧官能团不同所引起的；在同一种煤中，CO₂的扩散系数均小于N₂的扩散系数，表明煤吸附两种气体后N₂的扩散能力相较于O₂更强，即CO₂有更强的吸附能力。这是由于两种气体均为非极性分子，但CO₂的偶极矩更大，与含氧官能团产生相互作用更强，阻碍了CO₂的扩散。

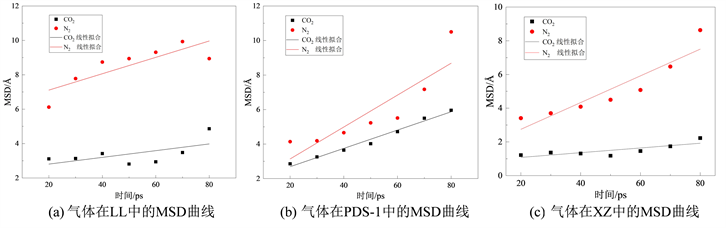
Figure 9. MSD curves of CO₂ and N₂

图9. CO₂与N₂的 MSD曲线

4. 结论

1) 在三种不同挥发分烟煤分子模型中，两种气体的吸附量大小顺序为CO₂ > N₂。随着压力的增加，两种气体逐渐达到极限吸附量，吸附速率也随之减小。低挥发分烟煤上的气体比高挥发分烟煤更容易达到极限吸附容量。在同一种煤中，达到吸附极限量由易到难的顺序为CO₂ > N₂。

2) CO₂和N₂的吸附热分别为31.8~34.4 kJ/mol和19.1~22.3 kJ/mol，两种气体的吸附热均小于40 kJ/mol，属于物理吸附。并且在303.15 K~323.15 K温度下，两种气体吸附热变化不明显，对于温度、压强并不敏感。

3) CO₂在不同挥发分烟煤的扩散系数为2.333 × 10⁻¹⁰ m²/s~8.840 × 10⁻¹¹ m²/s；N₂在不同挥发分烟煤的扩散系数为7.935⁻¹¹ m²/s~1.541 × 10⁻¹⁰ m²/s。在不同挥发分烟煤分子中，气体扩散能力的大小顺序为N₂ > CO₂，证明CO₂有更强的吸附能力。

项目基金

国家自然科学基金资助项目(52074122)。