欠压脱扣器操动装置用复位弹簧的应力松弛分析

Stress Relaxation Analysis of the Reset Spring Used in the Operating Device of Underpressure Trip

摘要: 欠压脱扣器在高压断路器起着重要的保护作用。当断路器电压下降到额定工作电压35%时，欠压脱扣器闭合使断路器停止工作。欠压脱扣器的关键部件之一是安装于其外部的采用复位弹簧实现储能的操动装置，为评估长期服役下复位弹簧的储能性能，对复位弹簧在同一应力水平不同温度下的应力松弛进行有限元分析，建立复位弹簧的应力松弛模型；使用SCDM右旋方式建立不同结构参数复位弹簧的有限元模型，完成应力松弛仿真分析，得到200℃下复位弹簧的应力与时间的变化规律，拟合出负荷损失率与时间对数lnt关系图，确定复位弹簧的应力松弛率；基于不同的线径d，外径D，节距t等结构参数的复位弹簧模型，得到复位弹簧结构参数与应力松弛率间的对应关系，为提高复位弹簧使用寿命提供依据。

Abstract: The undervoltage release plays an important protective role in the high voltage circuit breaker. When the circuit breaker voltage drops to 35% of the rated operating voltage, the undervoltage trip is closed and the circuit breaker stops working. One of the key components of the undervoltage re-lease device is the operating device which uses the reset spring to realize energy storage. In order to evaluate the energy storage performance of the reset spring under long-term service, the stress relaxation of the reset spring under the same stress level and different temperatures was analyzed by finite element method, and the stress relaxation model of the reset spring was established. The finite element model of reset spring with different structural parameters was established by SCDM right rotation mode. The stress relaxation simulation analysis was completed to obtain the variation law of stress and time of the reset spring at 200˚C, and the relationship between load loss rate and time log lnt diagram was fitted to determine the stress relaxation rate of the reset spring. Based on different structural parameters such as wire diameter d, outer diameter D, pitch t and so on, the corresponding relationship between the structural parameters of the reset spring and the stress relaxation rate is obtained, which provides a basis for improving the service life of the reset spring.

1. 引言

在高压断路器设备中，欠压脱扣器起着重要的保护作用。当高压断路器电压下降到额定工作电压的35%时，欠压脱扣器闭合使断路器停止工作。欠压脱扣器的关键部位是安装于外部的操动装置，该装置采用复位弹簧来实现储能。高压断路器一般使用寿命为20年，为评估满足服役要求下复位弹簧的储能性能，对其主要失效形式应力松弛进行仿真分析研究。

弹簧失效的模式并非单一，应力松弛是其最主要的失效模式 [1] [2] 。长期工作的弹簧元件，必须考虑应力松弛对其工作性能的影响 [3] [4] ，避免因弹簧元件性能衰退造成机构或系统无法实现预定功能。

国内外研究者，如：Goyal S [5] 等针对2.25Cr-1Mo铁素体铁焊接件进行了823 K温度下应力范围为100~240 MPa的蠕变试验，采用有限元方法针对IV型裂纹行为进行了预测；Grachev.SV [6] 考虑钢制弹簧条的碳含量在0.1%~1.0%之间对其机械性能的影响，研究表明硬化弹簧条的抗松弛性是回火温度和碳含量的函数；Seshadri等 [7] 采用广义局部应力应变法(GLOSS)以单轴应力松弛为基础建立了多轴应力松弛方程；李腾 [8] 对不同温度和不同载荷下弹簧试样的蠕变和应力松弛进行了研究，通过退化函数和Arrhenius模型对弹簧温室下蠕变和应力松弛服役寿命进行了预测；农鑫和高金忠 [9] 对100℃、140℃、180℃和220℃下的1Cr18Ni9弹簧进行了应力松弛试验，发现了100℃松弛过程一阶段和二阶段时间拐点较其它温度不明显，并通过从微观的松弛机理分析了100℃松弛曲线呈现的不同趋势；王柯和师俊平 [10] 设计搭建了弹簧应力松弛连续动态测试装置，基于蠕变理论及弹簧受力特点得到了蠕变本构方程，测得了仿真结果和实验误差相差不大于4%；金丹和刘兵 [11] 采用Abaqus对60Si2Mn钢制弹簧在同一应力水平下不同温度的应力松弛实验结果进行了有限元模拟，应力松弛模拟结果与实验结果吻合较好，随着温度的升高，模拟结果与实验结果误差值逐渐变大；周勇和周北岳 [12] 基于ANSYS分析了断路器弹簧，对初始应力的大小与蠕变应力松弛速率进行了研究；赵华和王延喜 [13] 基于硅锰合金弹簧钢扭转应力松弛实验提出了新的动力学方程，将其嵌入Abaqus，利用Creep子程序修正时间硬化蠕变模型，对400℃下的硅锰合金弹簧钢扭转应力松弛行为进行了数值模拟。

综上，国内外研究者目前主要以温度和载荷为变量对弹簧进行应力松弛研究，未从弹簧结构参数角度进行应力松弛分析。

本文基于高压断路器的服役条件、松弛动力学曲线和传统松弛理论建立欠压脱扣器操动装置用复位弹簧的应力松弛模型，分析不同结构参数下复位弹簧应力松弛率的变化规律，提出减小复位弹簧应力松弛的措施，具体流程图如图1所示。

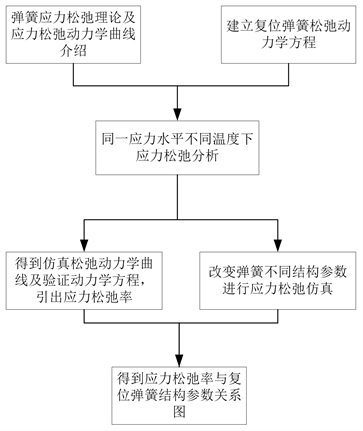
Figure 1. Stress relaxation simulation flow chart of the reset spring

图1. 复位弹簧应力松弛仿真流程图

2. 复位弹簧应力松弛模型建立

2.1. 弹簧应力松弛理论简介

图2所示的典型应力松弛曲线一般分为两个阶段：ab段为第Ⅰ阶段，第Ⅰ阶段持续时间较短，在该阶段内应力随时间急剧下降，但下降速度逐渐降低，趋于一个平稳值；bc段为第Ⅱ阶段，第Ⅱ阶段应力随时间延续而缓慢降低，甚至趋向一恒定值，且接近线性 [14] 。

由此可知应力松弛过程可用应力松弛曲线来描述。应力松弛曲线的各项特性指标中，松弛率最为重要。应力松弛有多种表达方式：

1) 用应力形式表示： $\frac{{\sigma }_0-\sigma }{{\sigma }_0}\times 100\%$ 或 $\frac{{\tau }_0-\tau }{{\tau }_0}\text{×}100\%$ 。

2) 用负荷损失率形式表示： $\frac{\Delta P}{P_0}\text{×}100\%$ 。

因需描述在发生应力松弛时弹簧的应力松弛率和自身结构参数之间的关系，故选用负荷损失率的表示方法。由此获得复位弹簧松弛的动力学基本方程 [4] 为：

$\Delta P/P_0=A+Bln{t}_R$ (1)

其中， $p_0$ 为弹簧初始载荷； $\Delta P$ 为弹簧载荷损失量；A，B为温度相关参数； $t_R$ 为松弛时间。

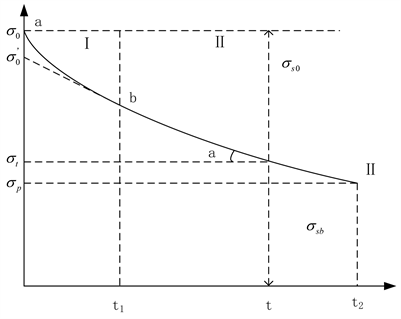
Figure 2. Typical stress relaxation dynamics curves

图2. 典型的应力松弛动力学曲线

2.2. 欠压脱扣器操动装置建模

欠压脱扣器操动装置的工作原理如下：用复位弹簧2套在U型块圆柱1和圆柱支座3外，当拉动拉锁软管4进而带动U型块1移动时，圆柱支座4挤压复位弹簧2压缩且同步移动。其三维模型如图3所示。

1-U型块圆柱，2-复位弹簧，3-圆柱支座，4-拉锁软管。

Figure 3. 3D model of undervoltage trip operating device

图3. 欠压脱扣操动装置三维模型

2.3. 复位弹簧有限元模型建立

基于ANSYS-SCDM采用右旋方式建立复位弹簧有限元模型(图4)，具体参数如下：弹簧外径D = 12 mm，弹簧丝直径d = 1.2 mm，节距t = 3 mm，自由高度h = 72 mm，复位弹簧上下端各增加高度h₁ = 4 mm，节距t = 1.5 mm的弹簧圈数n = 2，且两端削平，以便施加载荷作用。

Figure 4. Finite element model of reset spring

图4. 复位弹簧有限元模型

2.4. 不同温度下复位弹簧应力松弛仿真

以温度为应力松弛仿真模拟条件，一般要求温度点不少于4个 [10] 。若条件设置越多，建立的加速方程越精确，但对应的样本数也会增加 [10] 。这里选定100℃、150℃、200℃、250℃、300℃五个温度点对复位弹簧有限元模型进行应力松弛仿真分析。

在ANSYS中选用蠕变方程并输入蠕变常数，导入SCDM并建立复位弹簧模型。在workbench中改变温度数据，得到100℃、150℃、200℃、250℃、300℃下复位弹簧的应力随时间变化规律，如图5所示。

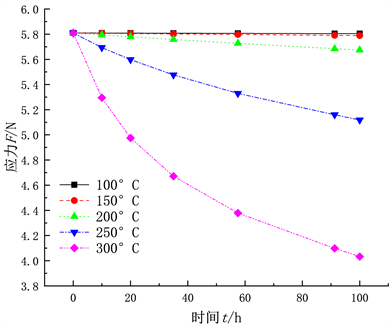
Figure 5. Stress relaxation curves at different temperatures

图5. 不同温度下的应力松弛曲线

由图5可知，各温度下的应力松弛曲线变化趋势相同，即各温度应力松弛过程表现出两个阶段：第一阶段曲线斜率较大，表明应力衰减迅速，持续时间短；第二阶段，曲线斜率较小，持续时间较长，表明应力衰减逐渐平缓，松弛率也趋向定值。

图5中弹簧应力与时间呈非线性关系，现对各温度下复位弹簧的仿真曲线做线性处理。以时间对数 $lnt$ 为横坐标，负荷损失率 $\Delta P/p_0$ (其中 $p_0$ 为初载)为纵坐标，分别对100℃、150℃、200℃、250℃、300℃五个温度点复位弹簧的仿真曲线进行处理，如图6所示。

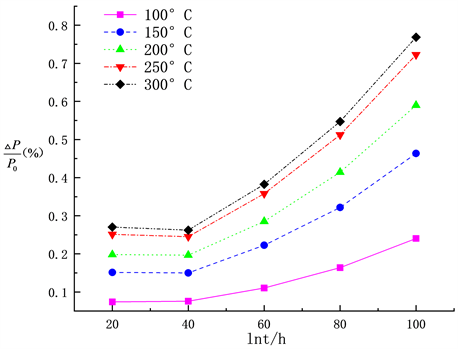
Figure 6. Relationship between load loss rate and logarithm of time

图6. 负荷损失率与时间对数关系

由图6可知，经处理复位弹簧的不同温度下的应力松弛曲线呈线性关系，说明负荷损失率与时间对数成正比。即在相同初始载荷下，直线斜率即是应力松弛率，可表示为：

$v_s=d\left(\frac{\Delta P}{P_0}\right)/d\left(lnt\right)$ (2)

由式(2)可知，复位弹簧的应力松弛率随温度升高而增大，对应力松弛率表达式两边积分得：

$\Delta P/P_0=C+v_{s}lnt$ (3)

其中， $\Delta P/P_0$ 为负荷损失率；C为积分常数。

由此拟合出式(3)与上述松弛动力学通式(1)吻合，说明通过复位弹簧应力松弛仿真分析得到应力与时间的非线性关系，通过拟合外推为负荷损失率与时间对数 $lnt$ 关系，符合复位弹簧应力松弛基本动力学方程 [4] 。

3. 复位弹簧的应力松弛分析

3.1. 蠕变参数设定

根据欠压脱扣操动装置用复位弹簧2模型(图2)，建立右旋复位弹簧的有限元模型。

基于workbench采用Norton公式 [15] 得到蠕变常数见表1。

Table 1. Creep constants

表1. 各温度下的蠕变分析参数

3.2. 复位弹簧边界设定及网格划分

如图4所示，复位弹簧上切面为载荷施加面，且整个弹簧只保留Z方向自由度；弹簧底面为固定平面。施加载荷选用压缩10 mm位移量作为应力松弛模拟的加载量。

在workbench中，对复位弹簧模型进行网格划分，弹簧单元选择SOLID186类型单元，获得了16,984个弹簧单元，其中复位弹簧的部分网格如图7所示。

Figure 7. Meshing of finite element model of reset spring

图7. 复位弹簧有限元模型网格划分

3.3. 不同结构参数复位弹簧应力松弛仿真

复位弹簧结构参数为原始值时，即弹簧线径d = 1.2 mm，外径D = 12 mm，节距t = 3 mm。改变复位弹簧不同结构参数，得到15类复位弹簧的三维模型，见表2。在ANSYS中对每个复位弹簧模型设定相同条件下，即在200℃试验温度和压缩10 mm位移量下进行应力松弛分析。

Table 2. Structural parameters of spring

表2. 弹簧结构参数

在workbench中对复位弹簧进行应力松弛模拟。当温度增加到300℃时，复位弹簧应力松弛现象明显。如图5所示，在300℃时应力随时间变化明显，复位弹簧储能效果降低，第一阶段曲线斜率变化大，表明应力衰减迅速，持续时间短；第二阶段，曲线斜率变化较小，持续时间较长，表明应力衰减逐渐平缓，松弛速率也趋向定值，应力衰退值大。

为降低复位弹簧应力松弛特性的影响，不改变温度载荷，研究复位弹簧的结构参数对应力松弛特性的影响，分别进行15类不同结构参数复位弹簧应力松弛仿真，得到200℃下的复位弹簧的应力–时间曲线如图8所示。

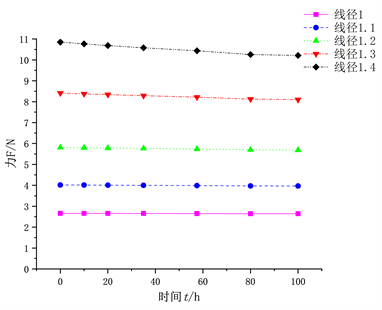(a) 不同线径d的复位弹簧 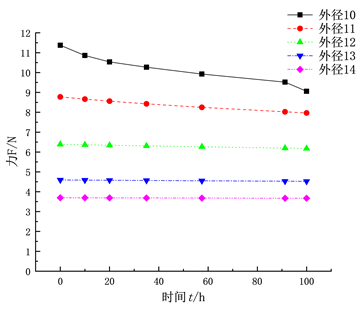(b) 不同外径D的复位弹簧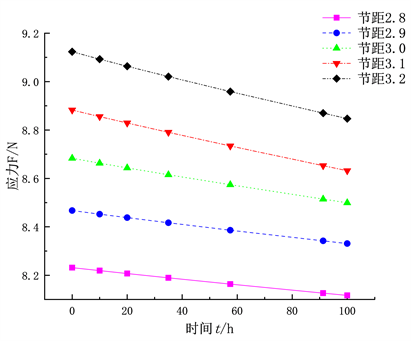(c) 不同节距t复位弹簧

Figure 8. Relationship between reset spring stress and time under different structural parameters

图8. 不同结构参数下复位弹簧应力与时间关系

另外，为研究复位弹簧结构参数对应力松弛特性的影响，对以上不同结构参数的复位弹簧应力–时间曲线通过公式(1)转化为负荷损失率和 $lnt$ 图，如图6所示。

由公式(2)可知，弹簧的应力松弛率是负荷损失率和 $lnt$ 曲线图的斜率，由此可把图8拟合为负荷损失率和 $lnt$ 关系图；再通过计算负荷损失率和 $lnt$ 图的斜率(应力松弛率)，得到复位弹簧的应力松弛率和结构参数关系图，如图9所示。

由图9可知，复位弹簧应力松弛率随复位弹簧的线径和节距递增，复位弹簧应力松弛率随复位弹簧的外径递增而变小。复位弹簧的线径d、外径D、节距t对于复位弹簧应力松弛特性呈非线性影响。所以原来复位弹簧外径D = 12 mm，丝径d = 1.2 mm，节距t = 3 mm在考虑应力松弛的基础上，复位弹簧结构参数为外径D = 14 mm、丝径d = 1.0 mm、节距t = 2.8 mm应力松弛特性差，可以提高复位弹簧使用寿命。

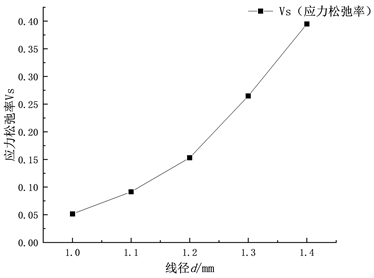(a) 不同线径d的复位弹簧 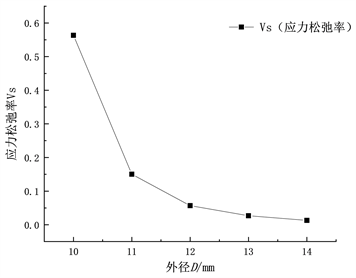(b) 不同外径D的复位弹簧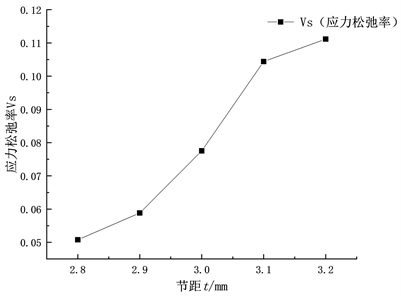(c) 不同节距t的复位弹簧

Figure 9. Relationship of stress relaxation rate of reset spring under different structural parameters

图9. 不同结构参数下复位弹簧的应力松弛率关系

4. 结论

基于workbench的蠕变模块对某型高压断路器用欠压脱扣器操动装置复位弹簧进行了应力松弛仿真分析，得到了弹簧应力松弛率随结构参数线径d、外径D、节距t的变化规律，主要结论如下：

1) 当复位弹簧节距t增加0.1 mm时，应力松弛率Vs提高1.51%；当线径d增加0.1 mm时，应力松弛率Vs提高8.58%；当外径D增加1 mm时，应力松弛率Vs降低13.76%。复位弹簧外径D和线径d对应力松弛特性的影响较大，节距t次之。

2) 使用workbench进行应力松弛仿真分析，仿真分析的应力松弛曲线与经典应力松弛动力学曲线同一规律，验证应力松弛理论和仿真的正确性。

3) 分析弹簧结构参数对于应力松弛特性的影响，得出外径D和线径d是影响复位弹簧应力松弛速率的主要参数，为提高弹簧服役寿命提供理论指导。

基金项目

国家重点研发计划项目(2018YFB1308100)；国家自然科学基金项目(51375458)。

NOTES

^*通讯作者。