1. 引言
总所周知,习近平总书记在2016年12月的全国高校思想政治工作会议上强调各类课程都要与思政理论课同向同行,形成协同效应 [1] 。2019年,在教师座谈会上进一步提出,要坚持显性教育和隐式教育相统一,发掘其它课程和教学方式中蕴藏的思想政治教育资源,实现全员、全程、全方位育人 [1] 。数学分析这一课程内容广、概念多、理论性强、抽象,这些特点导致学生学习的兴趣不高,在该课程中融入思政元素,一方面使学生通过形象具体的案例对专业知识有更加透彻的认识,从而激发学生的学习兴趣,促进专业知识的学习;另一方面,思政元素的融入,将引导学生形成科学的历史观,增强民族自豪和责任心。
2. 课程思政体系化设计思路及模式
对于《高等学校课程思政建设指导纲要》《山西省高等学校课程思政建设实施方案》等文件要求的贯彻落实,《数学分析》课程结合培养方案和毕业要求,认真思考了“培养什么人,怎样培养人,为谁培养人”这一问题,并且坚持课程思政隐性教育 [2] 。课程建设是“主战场”,课堂教学是“主渠道”,在充分考虑课程性质、课堂建设的已有资源、课程思政目标的设定、教学效果反馈等多种教学要素的基础上,提出了CRPE的设计思路,即课堂、教学资源、实施及评价与反馈四维模式。将“点线面体”的课程思政设计模式应用到该课程的课堂教学中,从而达到思政元素和专业教学有机融合,专业讲授和价值引领有机统一。
在相对比较枯燥的数学分析教学课堂中进行课程思政,首先要进行思政元素的凝练,然后将思政元素有效地、润物细无声地融入到专业知识点中。为此,提出了点、线、面、体的四维课程思政设计模式,即凝练“思政教育点”、梳通“思政教育线”、组合“思政教育面”、搭建“思政教育体”(图1)。
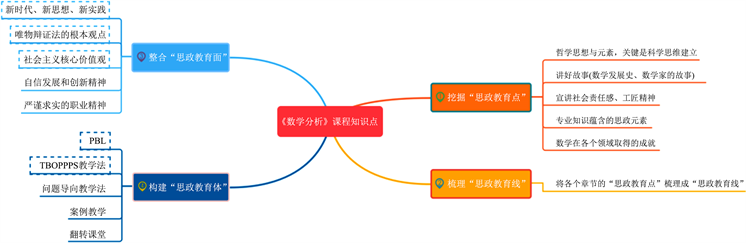
Figure 1. New mode of four-dimensional curriculum ideological and political design: point, line, surface and body
图1. 点、线、面、体的四维课程思政设计新模式
1) 凝练“思政教育点”
思政教育点的挖掘是课程思政的基础,需要教师或教学团队深入分析教学知识点,从中发现思政元素,进行讨论,采用挖掘–融入–再挖掘这一动态迭代过程,凝练思政教育点;另外,积极鼓励和要求学生参与大讨论、大分享,促进课程思政的有机融入。目前,在课程团队每周一次的集体备课和思政教学研讨下,搜集并提炼了大量的思政教育点。
2) 梳通“思政教育线”
课程思政要有一条主线,基于一条主线,不是为了思政而思政。结合课程目标将数学分析知识中蕴含的思政教育点疏通为五条主线:一是通过教学内容中蕴含哲学思想与元素,帮助学生树立正确的人生观、世界观、价值观;二是通过讲各种故事,激发专业学习兴趣,形成良好的品德修养;三是结合热点话题进行思政,增强学生的社会责任感;四是采用不同的教学方式、教学内容,如分组讨论、主题活动等,让学生树立好奉献精神和行业准则意识;五是讲述我国在各领域所取得的成就,增强民族自豪感和使命感。
3) 组合“思政教育面”
五条思政主线组合整理为五大思政教育面:社会主义核心价值观、自信发展和创新意识、社会责任感、教师教育职业精神、唯物辩证法的根本观点。
4) 搭建“思政教育体”
将融合后的思政教育面结合不同的教学方法和教学手段在数学分析课程中进行实践,从而构建了“思政教育体”。这既丰富了课堂内容,活跃了课堂气氛,又提升了教师教书育人的意识和水平,同时也达到了专业课程思政的目标。
3. 课程思政融入点及实现方式
3.1. 利用数学知识蕴含的哲学思想与元素融入思政教育
数学分析中的概念、定理非常多而且抽象,教师应尽量与实际生活中的一些现象练习,和学生产生共鸣,从而揭示一定的人生哲理。例如讲解函数连续性的概念时,教师可以举一些整容手术、悟空七十二变、女大十八变、揠苗助长的故事,从而延伸到现实生活中很多事物都是连续变化着的,不能急于求成,必须遵循事物发展的规律。函数凹凸性与拐点蕴含的人生哲理:人生成长的道路是曲折的,但前途是光明的,人生的每一个拐点都可视为人生的一个亮点。将有限项的和推广到无限项的和的级数理论揭示了辩证唯物主义思想中量变到质变的规律等。
3.2. 利用数学史和数学家的故事融入思政教育
数学分析课程中蕴含着丰富的数学史,教师可先布置一些查阅任务,让学生在任务驱使下了解一些概念的来源、背景或者发展史,如函数、微积分等的发展史以及李善兰、狄利克雷、黎曼等数学家的故事激发学生的民族自豪感和责任感。例如在讲级数收敛性时,可通过介绍割圆术求圆的面积以及中国古代的庄子《天下篇》中对一尺之锤的描述引出课题,一方面培养学生一般到抽象的思维过程,另一方面让学生了解我国数学方面的辉煌成就,增强学生的爱国情怀,增强民族自豪感和使命感。
3.3. 结合热点话题融入课程思政
热点话题是当代大学时比较感兴趣的,在数学分析的课堂教学中可借助热点话题进行思政教育。如借助“电信诈骗”的案例强调逆思维的重要性,进而引入导数的逆运算——不定积分。学习定积分的几何应用时,让学生分组讨论并计算赵州桥拱形面积和弧长;通过介绍建设港珠澳大桥的过程中,建筑师们保护中华白海豚的故事,体会建设者精益求精、追求卓越的“大国工匠”精神,培养学生学以致用、勇于探究的科学精神。
3.4. 结合有效的教学模式融入课程思政
课程思政的实施,除了挖掘思政切入点,切实可行的教学模式直接影响思政教育的效果 [3] 。在教学实施过程中,需要根据教学内容采用PBL、BOPPPS教学法、问题导向式教学和翻转课堂等教学方法和教学手段进行教学。对概念性的内容注重问题驱动法和启发式教学,如反常积分概念的引入;对理论内容,侧重研究性教学法,如实数完备性定理的证明;对应用性内容,着眼于讨论式和参与式,如微积分在物理与几何中的应用。采用不同的教学手段,利用信息技术将一些思政元素和课程内容可视化,吸引学生的注意力,激发学生的学习兴趣。如学习条件极值时,在课堂上带上一罐啤酒,请学生思考易拉罐为什么要这样设计?引导学生分析问题,解决问题,比较两种设计方案的用料说明市场上常见的易拉罐设计成这样的原因。将所学知识用于实际生活中,激发学生学习数学的兴趣,并引导学生节约资源,关注环境保护。
3.5. 利用中国各领域的伟大成就融入课程思政
开学第一课可通过介绍数学在航天、医疗、建筑、人工智能等领域的应用,让学生感悟任何领域都离不开数学,明白数学来源于生活;再如讲解导数概念时通过舰载机的起飞引入课题,同时播放我国在舰载机方面取得的成就,让学生树立远大理想和爱国主义情怀,承担肩负历史的使命。
4. 数学分析课程思政实施过程的反思
由于课程节数限制,不能将数学家的故事、数学史、数学在各领域的成就等相关内容进行全面的介绍,另外在某些方面内容还需要进一步丰富;其次,课程的平台功能需要进一步挖掘,由于是第一次使用超星泛雅平台,初期对于平台不够熟悉,有些功能还不能发挥,比如平台中的PBL功能,因此,需要进一步熟悉平台,挖掘平台中更有利于课程思政建设的功能 [4] 。从学生角度考虑,学生实践环节欠缺。由于数学分析课程本身理论性非常强的特点,导致课程建设实施过程中实践环节欠缺,虽然存在分析问题、解决问题的实践环节,但还很单一。
基金项目
省级项目:1) 《数学分析》课程混合式教学的应用研究,吕梁学院,教改项目(XJJG202102),主持;2) 山西省一流课程,山西省教育厅,(批准号:201801D21009);3) 山西省“1331工程”立德树人“好老师”支持课程——数学分析,山西省教育厅,(批准号:JYYB201409)。