1. 引言
随着中国经济发展,我国已成为世界第一汽车产销市场,而环境污染和能源问题也成为了摆在中国发展道路上的严肃问题,环境污染和能源危机问题也成为世界汽车行业关键技术的导向标。由于环境安全问题和能源安全问题逐渐进入各国研究学者的视野,同时每个国家都对传统燃油汽车设定了日渐严格的汽车污染物排放阈值。因此投入研发力量发展节能汽车与新能源汽车已成为未来汽车的发展趋势。动力电池及其管理技术是生产研发环保、节能、安全的节能与新能源汽车中的关键技术,而动力电池热管理技术又是动力电池及其管理技术中的重要一环 [1] 。一般来说纯电动汽车安全问题(如过热、燃烧、爆炸)主要是由于电池散热不当造成的,同时电池的散热不佳同时也会影响汽车的经济性、动力性、充放电效率和使用寿命,因此,需要设计最优的散热流道,来加快电池包夜冷板热量释放 [2] 。设计最优的散热通道分布形态,属于结构优化问题。结构优化是指在满足约束条件(设计要求)情况下,按预定目标求出最优的设计方案。为了设计最优的散热结构方案,必然涉及采用何种设计方法来实现的问题。
近年来,随着结构拓扑优化技术的发展,散热通道的分布形态优化设计逐渐展开,主要有三大类方法:一是基于构形理论的设计方法;二是基于结构拓扑优化技术的设计方法;三是仿生设计方法。本文采用的是基于拓扑优化技术的设计方法。拓扑优化方法优化方式的不同可分为:变密度法(Density based method)、均匀化方法(Homogenization method)、水平集法(Level-set based method)和结构渐进优化法(Evolutionary structural optimization method, ESO) [3] [4] 。
李昊等 [5] 以流体固体边界热交换量最大为数学模型的优化目标,采用变密度法进行液冷板散热流道的拓扑优化设计,研究了流量分配问题、热交换最大问题和多目标优化问题,并探讨了不同进出口布置方式和不同热源工况下优化结果的差异,将通过拓扑优化设计得到的散热流道与传统直流道的散热性能进行仿真及实验对比。Li等 [6] 采用渐进结构优化法对2D稳态热传导问题进行了尺寸优化和拓扑优化,给出均布热源、局部热源和多热源工况下的数值算例。
因此,本文为了得到最优的液冷板散热流道,利用商业有限元软件平台COMSOL Multiphysics对电池包液冷板散热问题进行拓扑优化设计,并将传统液冷板流道与拓扑优化得到的不同雷诺数下的液冷板的均温性能以及最大温差进行散热对比。
2. 建立数学模型
由于在实际工程应用中,雷诺数是表征流体流动速度的物理量,其大小变化也对拓扑形态产生影响,故本文探究雷诺数Re对流道形态的影响。在液冷流道拓扑优化中,设计域可以设计为存在许多孔隙的多孔介质材料,而在多孔介质材料中流体在其中流动收到的阻力F和流体流动的速度
成正比关系。表达式为
,其中的
为渗透率。通过有限元法,将设计域离散成有限个单元,每个单元都会被赋予一个设计变量
,
可以表示为0~1中的任意值,当
的时候,
此时趋近于无穷大,代表着固体域。当
的时候,
此时趋近于无穷小,代表着流体域。如图1所示。
对于不可压缩定常流动,需要描述流体流动中的连续性方程以及动量守恒方程。其中连续方程和能量守恒方程如下所示:
(1)
(2)
连续性方程表示流体的散度,由于采用的为不可压缩流动,所以流体的散度为0。式2中P表示流体的压力,V表示的是流体的速度矢量,f表示的流体所受到的外力矢量,本文中就是通过对渗透率的插值计算来对f进行表征,从而优化处流道形状。上文中
,中
表示渗透率,本文通过达西模型 [7] 对渗透率
进行插值:
(3)
式3中q为惩罚因子,本次试验设计中所取值为0.01。
与达西数和雷诺数的取值有着较大的关系,关系式如下:
(4)
流体中的传热公式主要由普朗特数Pr给出:
(5)
其中CP表示流体的比热容,kf表示流体的比热率。
其中的传热能量守恒方程如下所示:
(6)
使用牛顿冷却公式表达:
(7)
为了后续的拓扑优化以及得到清晰的流道,惩罚因子和达西数需要慎重的考虑,惩罚因子q选用的数值为0.01,达西数的选取需要设置为一个较小的数,本文选用10−4,普朗特数Pr取值为6.78,式7中的h的取值需要选取一个合适的值,才可以得到一个合适的流道形状,本文h取100。
3. 优化数学模型
为了使液冷通道获得最佳冷却性能,优化目标为设计域内生热量最大。由于热源产生的热量由流固边界传递给流体,最后由流体带出换热系统,故也可将目标函数视为流固边界换热量最大。优化数学模型如下:
(8)
式8中,
为设计域,
为设计域的总体积,
为热交换最大目标函数,
为进口边界,
流体流道所占的体积分数,取
。由于生热率随着
的增大而增大,为得到更大的换热面积,流道拓扑形态也会随着
的增大而增大而更加复杂,考虑制造约束,本文取
为100。优化迭代终止条件为:
,其中k迭代步数。
4. 不同雷诺数下优化结果
由于雷诺数是表征流体流动速度的物理量及大小变化对拓扑形态产生影响,因此,探究不同雷诺数Re (100 150 200)对流道形态的影响。验证不同雷诺数下优化的流道形状对结果的影响,如图2所示。


 Re = 100 Re = 150 Re = 200
Re = 100 Re = 150 Re = 200
Figure 2. Optimized flow channel morphology at different Reynolds numbers
图2. 不同雷诺数下优化流道形态
对比上图中的优化结果可以看出,随着雷诺数的不断增大,流道的数量也会不断的增多,以及流道的分支不断变细。并且平行同侧进出口布置流道,流道在靠近进出口一侧比较密集,且流道宽度较细,在远离进出口一侧比较稀疏,且流道宽度较粗。这是因为靠近进出口一侧通道距离短,流阻小,而远离进出口一侧流道距离长,流阻大,为使流量分配更加均匀,远离进出口一侧的流道需比靠近进出口一侧的流道宽度更大。
5. 仿真对比
本文的仿真实验对比主要是针对在不同雷诺数下的液冷板的均温性能以及最大温差来进行对比,还有就是针对市面上常见的传统液冷散热板的散热性能进行对比。
5.1. 建立传统液冷板流道模型
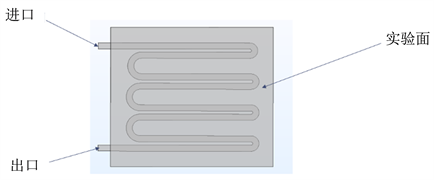
Figure 3. Simulation modeling of traditional liquid cooled plate
图3. 传统液冷板仿真建模
图3是液冷板及S型流道图,液体进出口分别位于液冷版的两端,流道截面为方形,其大小为8 mm*10 mm,厚度为8 mm;灰色区域为设计域,大小为450 mm*550 mm,其厚度为11 mm。
5.2. 液冷板及冷却液的选材
其中材料的属性定义为:常用作液冷板的材料有铝和铜两种,铜的导热系数高,用铜作为液冷板散热效果较好,但密度较高,大大增加散热系统的质量,且价格较高。综合考虑,液冷板的材料可选为铝,其参数如表1所示。

Table 1. Material property parameters of liquid cooled plate
表1. 液冷板材料属性参数
流体属性的定义:由于50%的乙二醇水溶液低温下不易凝固,各项参数满足液冷散热系统散热要求通常选用作为冷却液。本课题主要研究的冷却液的工作温度范围为20℃~40℃,选择其在20℃下的条件作为设置参数,具体为下表2所示。

Table 2. Attribute parameter values of coolant
表2. 冷却液的属性参数值
5.3. 设置边界条件
首先为了方便后续仿真完成后更好地读取结果,先定义一个实验面max,实验面min,实验面ave,实验面max以及实验面min以及进出口方向,如图3所示。设置流体初始速度为0.05 m/s,根据雷诺数的换算公式计算得出此时Re为1091。由于仿真的收敛速度不仅与网格类型和网格数量有关,还与初始条件的设置有关,合理的初始条件设置可加快收敛速度,减少计算时间,提高计算效率。所以设置初始温度条件时,可将空气的初始温度可设置为293.15 K,出口压力为0 Pa,壁面无滑移,实验面的广义热通量为500 W/m2。
5.4. 网格的划分
对液冷板进行网格细划分,最大单元数45.2 mm,最小为5.65 mm;对流道部分进行较细化划分,最大单元数31.1 mm,最小为2.26 mm。完整网格包含115,136个域单元、40,292个边界元和2975个边单元,如图4所示。

Figure 4. Grid division of traditional liquid cooled plate
图4. 传统液冷板网格划分
5.5. 仿真结果对比
针对三个不同雷诺数下的优化通道以及传统通道进行仿真对比。通过下图可以看出在相同的加热条件以及一致的外部条件下,针对四种不同的液冷板的温度云图进行对比,如图5所示。
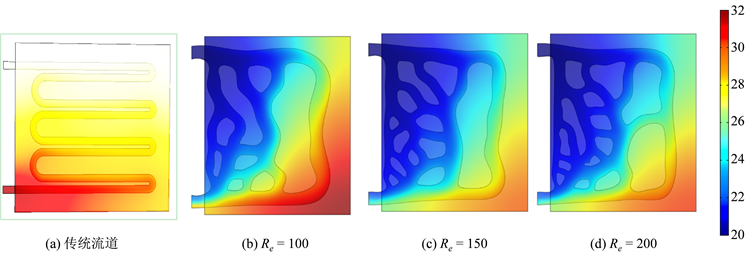
Figure 5. Temperature cloud map under different flow channels
图5. 不同流道下的温度云图
表3对上面的数据进行总结。

Table 3. Temperature under different flow channels
表3. 不同流道下的温度
5.6. 结论
1) 从上表3中很明显可以看出无论是从实验面的平均温度还是温差,拓扑优化出来的流道仿真出来的温度都比传统S型流道均温性以及散热性都要好。通过比较三个雷诺数Re所对应的拓扑优化通道形态可以看出:通道都随着雷诺数Re的增大而变得细密,这是因为热交换随着雷诺数的增大而增大,为了使目标函数(热交换)最大化,需增大流固换热边界面积,在体积分数相等的情况下,流道需更加细密以增加流固边界面积。
2) 随着雷诺数的增大,拓扑优化出来的流道经过有限元仿真得到的结果,当以
作为基准时,无论是实验面的平均温度还是温差,其误差值都非常的小,基本可以忽略不计。并且相较于传统直通道,拓扑优化通道温度更低,验证了其更优的流动、散热性能。
参考文献