基于气圈理论的帘子线直捻机纱线气圈稳态控制技术研究

Research on Steady-State Control Technology of Balloon for Direct Cabling Corder Based on Balloon Theory

摘要: 帘子线直捻机采用主动式送纱装置会引起气圈的不稳定。针对该问题，基于气圈理论提出了帘子线直捻机纱线气圈稳态控制方法。该方法对帘子线直捻机纱线气圈进行运动学分析，在MATLAB建立了气圈的运动学模型，通过数值模拟对比气圈不同部位半径波动情况。以此为基础，设置红外传感器检测气圈半径，霍尔传感器检测实时锭速，两个检测值组合成控制参数，与预设值进行对比后，采用传统PID控制器对送纱电机的转速进行闭环控制，实时调节气圈的形态。仿真结果表明，相同气圈形态时，气圈半径波动最大的位置不受纱线捻度、纱线密度和锭子转速的影响，具有良好的适用性。实验结果表明，不同纱线捻度、纱线密度和锭子转速情况下，该控制方法调节时间短，气圈形态稳定，误差区间在−3%~6%，即验证了该方法具有良好的控制效果和可行性。

Abstract: The active yarn feeding device used in the direct cabling corder will cause the instability of the bal-loon. In order to solve this problem, a steady-state control method for the balloon of direct cabling corder was proposed based on balloon theory. In this method, the kinematic analysis of the balloon in the cord twister was carried out, and then the kinematic model of the balloon was established in MATLAB. The change of radius of different parts of balloon during twisting was compared by nu-merical simulation. Based on this, the infrared sensor was set to detect the balloon radius, and the Hall sensor was set to detect the real-time ingot speed. The two detection values were combined in-to control parameters, and compared with the preset values, the traditional PID controller was used for closed-loop control of the speed of the yarn feeding motor, adjusted the balloon shape in real time. The simulation results show that the twist of yarn, yarn density and spindle speed have no ef-fect on the position with the largest fluctuation of the balloon when the balloon shape is the same. It means that the method has good applicability. The experimental results show that under different yarn twist, yarn density and spindle speed, the adjustment time of this control method is short, the balloon shape is stable, and the error range is −3%~6%. So this method good control effect and fea-sibility.

1. 引言

帘子线被广泛应用于材料领域，例如用作轮胎、运输带、传动带等橡胶制品的增强材料。在纺织行业中，直捻机生产帘子线时的能耗成本占生产总成本的4/5，主要来自实现加捻功能的锭子 [1] 。其中，锭子带动外纱旋转形成气圈所占能耗比例较高。帘子线的原料纱强度较高，可将传统直捻机的被动送纱方式改为主动送纱，通过控制送纱速度来改变外纱气圈的形态，最终减少帘子线直捻机的能耗 [2] 。主动送纱时，储纱盘上无纱线缠绕，无法自动调节外纱气圈张力，最终导致外纱气圈不稳定，影响捻线的品质 [3] 。因此生产中为了减小气圈波动、维持稳定的气圈形态，还需要通过控制装置对外纱气圈形态进行控制。

现在的气圈理论已经比较成熟，许多研究者将其应用于纺织机来解决问题。Cave和Fraser [4] 基于气圈理论，系统地研究了纱线张力对气圈稳定性的影响。Praček等 [5] 基于气圈理论改进了交叉卷绕筒子退绕过程，提高了退绕的稳定性。Chattopadhyay和Venugopal [6] 研究了真空压力、开罗辊速度和纱线的线密度不同情况下，转子纺纱过程中产生的空气阻力对纱线气圈张力的影响。MEI等 [7] 研究了锭子角速度、纱线细度等因素对直捻机气圈纱张力的影响，建立了直捻机纱线气圈张力的拟合方程。倪远和孟进 [8] 结合早期小直径气圈控制环构想和最新多波节气圈控制高速纺纱模型，提出了具有实际应用意义的开合式小直径气圈控制纺纱技术方案。Hossain等 [9] [10] [11] 研究了环锭纺纱过程中纱线张力和气圈形态，提出了一个数学模型来作为环锭纺纱过程中锭子速度的函数，同时引入超导磁轴承(SMB)系统，克服了环锭纺纱机的摩擦限制。刘汉邦等 [12] 考虑了空气阻力和科氏惯性力的作用，基于气圈理论提出了纱线卷绕半径和钢丝圈回转半径随时间变化的数学方程模型，能准确预测钢丝圈外倾角和前倾角随时间变化的规律。由此可知，气圈理论在纺织机械领域，特别是在环锭纺纱机应用较为成熟，但缺少以直捻机为对象的气圈研究。

综上所述，为了实现帘子线直捻机气圈的稳态控制，本文以TC21直捻机为研究对象，基于气圈理论提出了帘子线直捻机纱线气圈稳态控制方法。该方法基于气圈理论对直捻机的外纱气圈进行运动学分析，建立了外纱气圈的数学模型，通过数值仿真对气圈不同位置的波动大小进行对比分析，确认检测气圈波动的最佳位置。设置红外传感器检测气圈半径，霍尔传感器检测实时锭速，两个检测值组合成控制参数，与预设值对比后，采用传统PID控制器对送纱电机的转速进行控制，保证气圈的形态的稳定。

2. 结构及数学模型

帘子线直捻机将两根未加捻的单股原丝以缆捻方式直接捻合成帘子线，直捻机控制系统示意图见图1。外纱锭固定于机架上部，外纱在送纱电机的作用下，通过空心引纱管从锭子的底部进入储纱盘，从储纱盘出口被引出到匀捻器导纱孔。锭子电机带动外纱高速旋转，在加捻盘与匀捻器之间形成气圈。位于储纱罐中的内纱由内纱张力器引出，在匀捻器的作用下与外纱捻合，张力传感器实时检测纱线是否断纱。加捻后的纱线经过超喂电机和缓冲杆，最终卷绕在纱筒上，得到帘子线的成品。

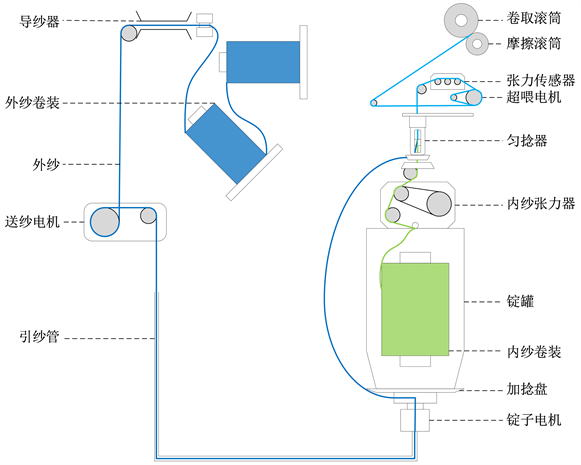
Figure 1. Unit yarn control system of a direct cabling machine

图1. 直捻机单元纱线控制系统

如图2所示，直捻机外纱由锥形锭盘段BD和气圈段AB两部分组成。锥形锭盘段BD为缠绕在储纱盘和加捻盘上的纱线，气圈段AB为锭子带动纱线自由旋转的部分。位于气圈段AB处的纱线需要克服摩擦力和空气阻力。因此气圈运动特性主要考虑气圈段AB的纱线。锥形锭盘段BD的纱线运动作为求解时的下端边界条件。

Figure 2. Path of the outer yarn

图2. 外纱的纱线路径

位于气圈段AB的纱线微元如图3所示。以气圈上部平齐的匀捻器中心点为坐标原点，建立一个静坐标系 $\theta \left(r,\zeta ,z\right)$ ，Z轴与纱线筒管的中心线重合，正方向为竖直向下。再定义一个动坐标系 $R\left(r,\theta ,z\right)$ ，坐标原点与静坐标系的坐标原点重合。该动坐标系绕Z轴旋转，角速度为 $\omega$ 。静坐标系相对动坐标系的位置表达式为：

$\zeta =\theta +\omega t$ (1)

其中：t为时间，s； $\theta$ 为纱线与动坐标系r轴的夹角，rad。

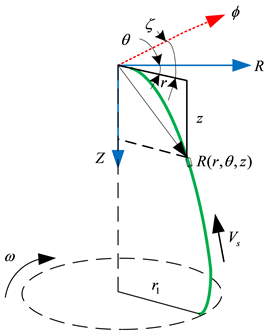
Figure 3. Moving coordinate system of balloon

图3. 纱线气圈动坐标系

分析动坐标系时，需要假设气圈段AB的纱线为一条静止的空间曲线。在气圈段AB上任取一点R，将坐标原点与该点之间的纱线长度记为s，该点的气圈半径记为r。取单位径向量为 $e_r$ ，Z轴单位向量为 $e_z$ ，由此可得位置矢量R为：

$R=r{e}_r+z{e}_z$ (2)

取单位角向量为 $e_{\theta }$ ，由此气圈上纱线的单位切向量可以表示为：

$\tau =\frac{\text{d}R}{\text{d}s}=r^{\prime }{e}_r+r{\theta }^{\prime }{e}_{\theta }+z^{\prime }{e}_z$ (3)

锭子回转角速度：

$\omega =\omega \cdot e_z$ (4)

纱线送线速度：

$v_s=-v_s\left(r^{\prime }{e}_r+r{\theta }^{\prime }{e}_{\theta }+z^{\prime }{e}_z\right)$ (5)

其中： $v_s$ 为纱线卷绕送线速度，m/s。

在气圈段AB上取纱线微元 $\text{d}s$ 进行分析， $\text{d}s$ 收到三个外力以及三个加速度的作用。可以得到纱线微元 $\text{d}s$ 的力平衡方程为：

$m_0\left(a_n+a_k+a_s\right)\text{d}s=\left(F_T+F_{pu}+F_{pt}+F_g\right)\text{d}s$ (6)

其中： $m_0$ 为纱线的线密度，dtex； $a_n$ 为向心加速度，m/s； $a_s$ 为相对加速度，m/s； $a_k$ 为科氏加速度，m/s； $F_T$ 为纱线所受张力，N； $F_g$ 为重力，N； $F_{pu}$ 为沿 $\text{d}s$ 法线方向的空气阻力，N； $F_{pt}$ 为沿 $\text{d}s$ 切线方向的空气阻力，N。

代入纱线微元的受力公式以及纱线微元的加速度公式，方程在静坐标系下的分量方程为：

$\{\begin{array}{l}{m}_0\left[v_s{}^2{r}^{″}-r{\left(v_s{\theta }^{\prime }+\omega \right)}^2\right]=T\left(r^{″}-r{{\theta }^{\prime }}^2\right)+T^{\prime }{r}^{\prime }+3m_{0}r{\omega }^2+p_n{r}^3{r}^{\prime }{\theta }^{\prime }{\omega }^2\sqrt{{r^{\prime }}^2+{z^{\prime }}^2}\\ m_0\left[2r^{\prime }{v}_s\left(v_s{\theta }^{\prime }+\omega \right)+r{v}_s{}^2{\theta }^{″}\right]=T\left(2r^{\prime }{\theta }^{\prime }+r{\theta }^{″}\right)+T^{\prime }r{\theta }^{\prime }-p_n{r}^2{\omega }^2\sqrt[3]{{r^{\prime }}^2+{z^{\prime }}^2}\\ m_0{v}_s{}^2{z}^{″}=T{z}^{″}+T^{\prime }{z}^{\prime }+m_{0}g+p_n{r}^3{z}^{\prime }{\theta }^{\prime }{\omega }^2\sqrt{{r^{\prime }}^2+{z^{\prime }}^2}\end{array}$ (7)

由于法向空气阻力系数是切向的20倍，故只考虑法向空气阻力对纱线的影响。由于法向空气阻力方向垂直于纱线，假定纱线是柔性无伸长的，可以得到：

$\frac{\text{d}R}{\text{d}s}\cdot \frac{\text{d}R}{\text{d}s}=1,\frac{\text{d}R}{\text{d}s}\cdot F_{pu}=0$ (8)

对纱线微元的力平衡方程点乘 $\text{d}R/\text{d}s$ ，得到：

$T^{\prime }=-m_0{\omega }^{2}r{r}^{\prime }-m_{0}g{z}^{\prime }$ (9)

忽略微元的重力，因此得到：

$T^{\prime }=-m_0{\omega }^{2}r{r}^{\prime }$ (10)

将式(10)代入式(7)中，最终化简得到气圈纱线运动方程：

$\{\begin{array}{l}{r}^{″}=\frac{T^{\prime }{r}^{\prime }+\left(m_0{v}_s^2-T\right)r{{\theta }^{\prime }}^2+m_{0}r{\omega }^2-2m_0\omega v_{s}r{\theta }^{\prime }+P_n{r}^3{r}^{\prime }{\theta }^{\prime }{\omega }^2\sqrt{{r^{\prime }}^2+{z^{\prime }}^2}}{m_0{v}_s{}^2-T}\\ {\theta }^{″}=\frac{r{\theta }^{\prime }{T}^{\prime }-2r^{\prime }{\theta }^{\prime }\left(m_0{v}_s^2-T\right)+2m_0\omega v_s{r}^{\prime }-P_n{r}^3{r}^{\prime }{\theta }^{\prime }{\omega }^2\sqrt{{r^{\prime }}^2+{z^{\prime }}^2}}{r\left(m_0{v}_s^2-T\right)}\\ z^{\prime }=\sqrt{1-{r^{\prime }}^2-{\left(r{\theta }^{\prime }\right)}^2}\\ T^{\prime }=-m_0{\omega }^{2}r{r}^{\prime }\end{array}$ (11)

根据直捻机实际尺寸对数学模型方程进行初值赋值，得到方程的以下条件：

a) 位于气圈顶端的导纱孔处的初值：

$r\left(0\right)=r_0,\theta \left(0\right)=0,z\left(0\right)=0$ (12)

其中： $r_0$ 为匀捻器导纱孔处半径，mm。

b) 位于气圈底端的加捻盘出口的初值：

$r\left(z_3\right)=r_1,z_3=h$ (13)

其中： $r_1$ 为加捻盘半径，mm；h为气圈高度，mm。

c) 纱线从储纱盘出口送出后，由于锭子的高速旋转，使得纱线在储纱盘上有一段包角 $\theta$ 。如图2所示，根据短程线理论，储纱盘上的纱线升角为：

${\alpha }_0=\frac{\text{d}z}{\text{d}s}=t{g}^{-1}\left[h_2/\left(2\pi r_2\frac{\theta }{360}\right)\right]$ (14)

其中： $h_2$ 为储纱盘纱线出口到加捻盘底部高度，mm； $r_2$ 为储纱盘半径，mm。

由此，可以得到纱线在储纱盘与加捻盘交界点C处纱线与水平的夹角。

位于圆锥锭盘上的纱线，由于储纱盘上的纱线包角不同，储纱盘与圆锥锭盘连接处的纱线与水平线的夹角也会不同。如图4所示，将圆锥锭盘的表面展开得到一个扇形面，根据短线程理论， $C{B}_1$ 为某一情况下可能的纱线路径。对于圆锥锭盘的锥顶角记为 ${\theta }_0$ ，因此展开的扇形面顶角 ${\theta }_1$ 为：

${\theta }_1=\pi \sin {\theta }_0$ (15)

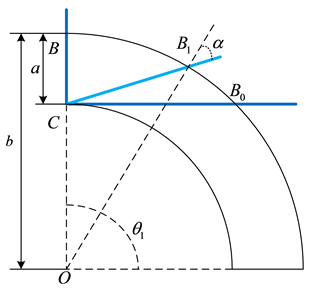
Figure 4. Expansion drawing of the over-run plate

图4. 加捻盘展开图

记OB长度为b，加捻盘长度CB为a。储纱盘上包角越大，纱线在圆锥锭盘上的路径越接近 $C{B}_0$ ；反之，包角越小，纱线在圆锥锭盘上的路径越接近CB，由此可以近似得到直捻机正常工作时 $\theta \left(z_1\right)$ 值的范围为：

$\theta \left(z_3\right)=\alpha >{\sin }^{-1}\left(\frac{b-a}{b}\right),\theta \left(z_3\right)<{90}^{°}$ (16)

其中： $\alpha$ 为 $C{B}_1$ 与 $O{B}_1$ 的夹角，rad。

d) 如图2所示，受锭罐大小的限制，气圈形态不能过小，由此可得纱线在锭罐上方 $z_1$ 和锭罐下方 $z_2$ 的半径最小为 $r_3$ 。

e) 纱线为柔性的材料，加捻过程中会被拉长。为了方便计算，假设纱线不可伸长，则可知 ${\theta }^{\prime }\left(0\right)=0$ 。

由此得到了气圈的数学模型，可以通过该模型对纱线的运动情况进行数值模拟，研究气圈波动时的纱线形态变化情况。

3. 仿真

为了探索气圈波动与气圈形态之间的联系，在MATLAB中对直捻机气圈的数学模型进行数值模拟，以找到更容易检测气圈波动的位置。对纱线气圈运动模型进行分析时，求解过程中必需的常量值对仿真过程影响较大，相关参数的选取需满足一定的实际条件。生产帘子线的常用材料为涤纶，选取涤纶作为模拟纱线的材料，求解分析过程中所需的参数见表1。

Table 1. Parameters used in the simulation

表1. 仿真参数设置

在实际生产过程中，由于不同的加工要求，直捻机的锭子转速一般在7000~9000 r/min之间。除了锭子的转速外，还需要选取不同捻度和不同密度的纱线进行对比，最终设置4组仿真参数见表2。

Table 2. Parameters of different groups

表2. 实验各组参数设置

纱线气圈的上下位置已经确定，故气圈形态可由气圈的最大半径概括。图5为4组仿真所得气圈得最大半径所在Z坐标。如图5所示，对于已确定结构及尺寸的直捻机加捻锭子组件，对于不同仿真参数，气圈最大半径所在Z坐标的位置变化曲线不变。同一参数时，气圈的最大半径位置会随着气圈形态的变化而变化，当气圈形态减小时，气圈最大半径位置下移。

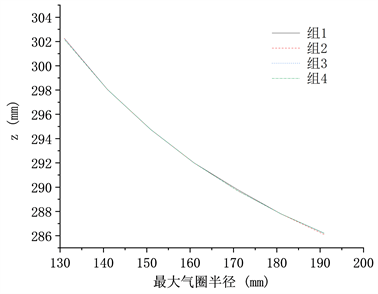
Figure 5. Position of the maximum radius of the balloon

图5. 气圈最大半径的位置

设置不同气圈最大半径的七组气圈，参数见表3。比较相邻两个序号的气圈半径，得到波动时气圈不同位置的半径变化，结果如图6所示。

Table 3. Grouping of the balloon shape

表3. 气圈形态分组

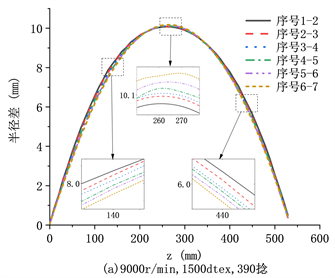
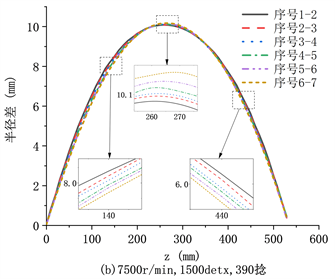
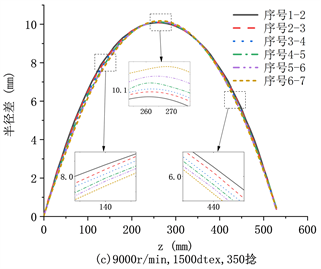
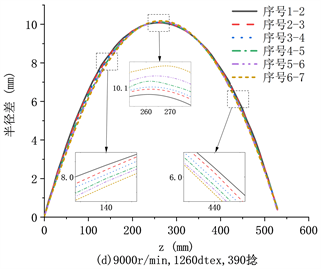
Figure 6. Simulation of balloon shape change

图6. 气圈形态变化仿真图

图6为四组仿真实验的气圈波动结果图。如图6(a)~(d)所示，在锭子转速、纱线密度和纱线捻度不同的情况下，气圈波动情况的结果相同。在气圈的坐标Z轴0 mm~220 mm和坐标Z轴350 mm~530 mm，气圈形态越大，波动越大；在气圈的坐标Z轴220 mm~350 mm处，气圈形态越小，波动越大；气圈半径波动最大的位置在坐标Z轴260 mm~270 mm之间，随着气圈形态变小而向下偏移。比较图5和图6，气圈半径波动最大的位置和气圈最大半径位置不重合，都随着气圈形态的变小而向下偏移。

以上仿真结果表明，气圈形态相同时，气圈半径波动最大位置不会偏移，且该位置下红外传感器更容易检测气圈的波动，具有良好的适用性。

4. 气圈的控制

直捻机外纱从储纱盘退绕，经过送纱器后再通过外纱张力器进入锭子电机中空轴。若给定相同的工艺参数，且储纱盘上纱线包角大于0度( $\omega >0^{\circ }$ )，则储纱盘回转运动能动态调节气圈张力，并保持气圈相对稳定。

当增大纱线张力至储纱盘上纱线包角接近0度( $\omega =0^{\circ }$ )，此时储纱盘上无卷绕的纱线，外纱直接从储纱盘出口进入加捻盘，因此储纱盘的功能失效。该情况下，在储纱盘前增大纱线张力可使纱线气圈明显减小，但气圈形态不稳定。因此主动控制气圈形态时，需进行外部控制以维持气圈的稳定性，进而保证捻线的品质。

考虑商业应用的情况，气圈控制系统采用传统PID的控制器，使用步进电机作为主动送纱装置，安装在加捻盘和外纱张力器之间的纱路上，通过红外传感器检测纱线气圈半径，霍尔传感器检测锭子电机的转速。控制方案见图7。

气圈的控制主要分为启动阶段和平稳阶段，两个阶段的需要采取不同的控制方法，各阶段控制方法如下：

a) 启动阶段，控制系统根据设定的纱线捻度，锭子转速等参数计算出送纱电机的目标转速，然后将控制参数传入PID控制器，PID控制器控制送纱电机在设定的加速时间内达到目标气圈形态。在送纱电机加速的过程中，根据红外传感器和转速传感器实时检测气圈的半径进行电机调速，进而减小启动阶段的过度控制。

b) 平稳阶段，根据实际情况，将控制频率设置为2 Hz，控制系统将红外传感器和电机传感器测得参数组合为控制参数，与预设值进行比较后将控制参数传入PID控制器，PID控制器控制送纱电机转速以改变纱线气圈的形态。实现纱线气圈主动控制的同时，保证气圈形态的稳定性。

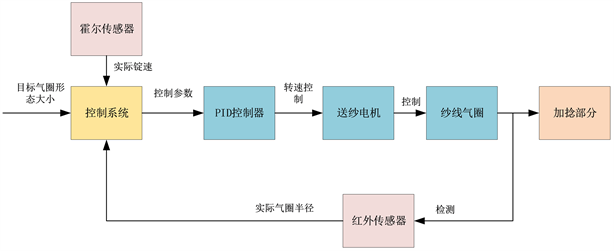
Figure 7. Schematic diagram of balloon control system

图7. 气圈控制系统示意图

上述直捻机外纱气圈的半径测量方案见图8，计算气圈半径大小的原理见图9。外纱随着锭子旋转，每旋转一圈切割红外线两次。记录两次切割之间的时间间隔为 $t_1$ ，纱线气圈的最大半径 $r_m$ 处，红外线距离锭子中心距离为 $l_1$ ，计算得到纱线切割红外传感线所旋转的角度 $\beta$ 为：

$\beta =\omega \cdot t_1$ (17)

由此可以计算得到外纱此时的气圈半径为：

$r=\frac{l_1}{\cos \frac{\beta }{2}}$ (18)

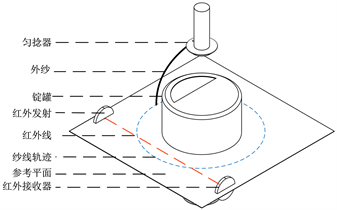
Figure 8. Infrared-sensor installation

图8. 红外传感器安装示意图

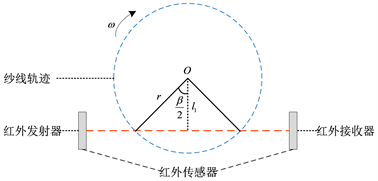
Figure 9. Principle of measuring the balloon radius

图9. 测量纱线气圈半径原理图

控制方案所采用的PID控制，是将系统预设值与实际检测值进行比较，得到的差值进行三种算法运算后重新控制对步进电机的输出量。连续控制的理想PID控制规律为：

$\mu \left(t\right)=K_P\left(e\left(t\right)+\frac{1}{T_I}{\displaystyle {\int }_0^{t}e\left(t\right)\text{d}t+T_D\frac{\text{d}e\left(t\right)}{\text{d}t}}\right)$ (19)

其中： $\mu \left(t\right)$ 为控制器输出的控制量； $e\left(t\right)$ 为偏差信号； $K_P$ 为比例积分； $T_I$ 为积分时间常数； $T_D$ 为微分时间常数。

考虑到系统的负担和实际应用，以及位置式PID控制算法和增量式PID控制算法对控制系统的影响情况，最终计算采用增量式控制算法。

对上述PID系统进行离散化，把连续状态的公式(19)进行整理，得到增量式PID：

$\begin{array}{c}u\left(k\right)=u\left(k-1\right)+\Delta u\left(k\right)\\ =K_p\left[e\left(k\right)-e\left(k-1\right)\right]+\frac{1}{T_I}e\left(k\right)+T_D\left[e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right)\right]\end{array}$ (20)

其中：K为采样的序号； $u\left(k\right)$ 为控制增量。

在对PID的三个参数进行调整时，首先调整 $T_I$ 直至气圈能控制在目标形态附近，此时气圈波动较大。再调整 $K_P$ ，使得气圈波动减小，达到较稳定的气圈形态。最后再调整 $T_I$ 和 $T_D$ ，减小控制系统启动阶段的气圈形态过度调整，降低断纱的可能。

5. 实验

为了研究该控制方法的控制效果，以TC21型帘子线直捻机作为对象搭建了实验平台，见图10，其中直捻机锭子的各项参数如表4所示。

Figure 10. Experimental platform

图10. 实验平台实物图

Table 4. Parameters of direct cabling corder in the experiment

表4. 实验中直捻机的参数

实验只启用直捻机的一个工作单元。直捻机使用主动送纱，设置红外传感器对气圈切割红外线的间隔时间进行测量。控制系统对传感器所采集的数据进行处理后，自动控制送纱电机的转速，将气圈的形态控制在设定值的附近。

对实际情况下的机器气圈进行测量。气圈自由旋转时，气圈的半径 $r_m$ 值在185 mm和190 mm之间。控制送纱速度至纱线断线，此时气圈的半径 $r_m$ 设定值为133 mm。如图11所示，图11(a)和图11(b)分别为气圈的最大形态与最小形态，图11(c)和图11(d)为图片进行处理后的气圈形态轮廓。为了保证实验过程中纱线不会和锭罐摩擦而导致断裂，同时保证气圈在一个较小的形态，将气圈形态设定在 $r_m$ 为143 mm。

Figure 11. Balloon in the experiment

图11. 气圈实验图

由仿真结果可知，气圈不同位置的波动大小不同。为了比较气圈波动大小对气圈控制的影响情况，使用两对红外传感器。一对红外传感器负责检测固定位置的气圈半径，将各组实验的气圈形态控制在相同大小。另一对红外传感器作为控制系统的一部分，采集所得数据作为控制系统的输入量来控制外纱气圈。仿真所得气圈最大半径在平面坐标系Z轴为297 mm的位置，气圈波动最大位置在平面坐标系Z轴为265 mm的位置。固定位置的气圈半径检测的红外传感器设置在气圈半径最大位置。将气圈最大波动位置设为实验组，气圈平面坐标系Z轴140 mm位置设为对照组。实验分为4组，考虑锭子的转速，纱线的捻度和密度对实验的影响，所设置的不同组的参数见表5，实验所得结果见图12。实验分析结果见表6和图13。

Table 5. Parameter setting of each experimental group

表5. 实验各组参数设置

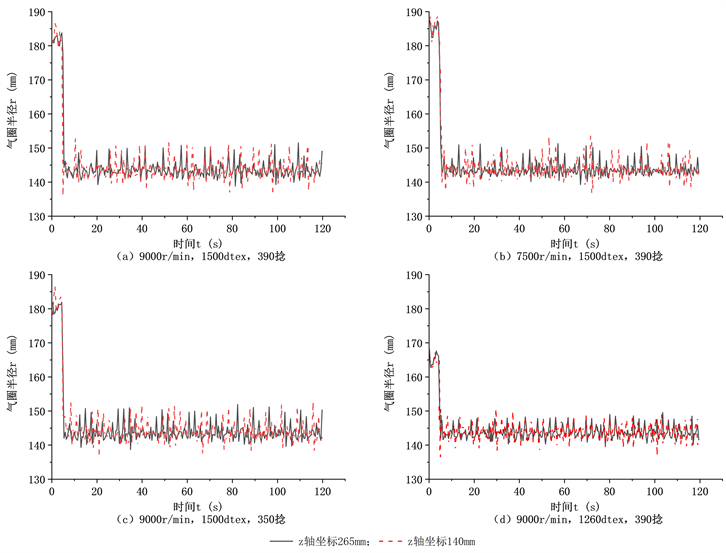
Figure 12. Fluctuation of the radius of the balloon

图12. 气圈半径波动情况

Table 6. Analysis of experimental results

表6. 实验结果分析

Figure 13. Fluctuation range of the balloon

图13. 气圈波动范围对比

启动阶段的气圈半径变化较大，过度控制会导致气圈远小于设定值，使得纱线与锭罐摩擦导致断线。如图12所示，红外传感器设置在坐标Z轴140 mm时，气圈控制的启动阶段出现了过度控制的情况，气圈半径过小；红外传感器设置在坐标Z轴265 mm时，气圈控制的启动阶段没有出现过度控制的情况。

如表6所示，在不同锭子转速，纱线的线密度和纱线捻度的实验中，红外传感器设置在坐标Z轴265 mm时气圈半径变化的方差较小，说明红外传感器设置在气圈最大波动处能有效降低气圈的波动。比较两种情况控制下固定位置气圈半径的均值、最大值和最小值，其均值与目标值的差值相似，但红外传感器设置在坐标Z轴265 mm时，对应的气圈半径最大值较小，最小值较大，说明红外传感器设置在气圈最大波动处能够有效地降低稳定阶段的气圈波动幅度。对比四组实验的方差，减小锭子的转速、增大纱线的捻度和减小纱线的线密度，都使得方差减小，降低气圈的波动。

6. 结论

本文以TC21型直捻机为对象，进行了模拟仿真和实验，得出了以下结论：

1) 提出了一种基于气圈理论的直捻机气圈稳态控制方法。该控制方法基于气圈理论找到更容易检测气圈波动的位置，再利用红外传感器和霍尔传感器对气圈形态进行实时检测，通过控制送纱速度将气圈形态稳定在预设值附近，能有效抑制直捻机主动送纱时气圈的波动，有利于加捻过程中气圈保持稳定，降低断纱的概率，进而保证捻线的品质。

2) 根据仿真的结果，对于已确定结构及尺寸的直捻机加捻锭子组件，气圈波动最大的位置与气圈最大半径位置不同，且随着气圈形态的减小而沿进纱方向偏移。此外，在气圈形态变化过程中，纱线捻度、纱线的线密度以及锭子转速对加捻过程中纱线气圈的整体半径变化情况影响较小，说明该方法具有良好的适用性。

3) 根据实验的结果，在不同锭子转速、纱线的线密度和纱线捻度的实验中，该方法能有效地将气圈形态控制在设定值附近，且误差区间为−3%~6%，即该方法能有效地稳定气圈。同时，红外传感器安装在仿真所得气圈半径波动最大的位置，能使在加捻启动阶段和平稳阶段的气圈波动更小，降低纱线断线的概率。

致谢

衷心感谢我的导师以及师兄师弟在课题研究和论文撰写过程中提供的支持。感谢浙江日发纺织机械有限公司提供的技术和设备支持。

NOTES

^*通讯作者。