基于RWEQ模型的土壤风蚀模数影响因素研究

Study on Influencing Factors of Soil Wind Erosion Modulus Based on RWEQ Model

摘要: RWEQ模型是定量研究土壤风蚀的关键模型，为深刻分析该模型在建模过程中各引入变量与土壤风蚀的关系，以土壤最大转移容量(Qmax)为描述变量，探究植被盖度、土壤粘粒含量与Qmax的关系，对植被盖度、土壤粘粒含量分段赋值，产生9898组变量组合，计算了气象因子为17、可蚀性因子为0.456、土壤粗糙因子为0.68、有机质含量为2%前提条件下的Qmax值，分析了各种组合条件下三者的关系，结果表明：1) Qmax值与植被盖度存在较明显的负相关关系，且40%植被盖度是抑制风蚀作用的重要节点盖度，在达到此盖度前植被具有剧烈的抗风蚀作用；2) 与上述方法相同，土壤粘粒含量也与Qmax值呈负相关关系，且土壤粘粒含量阈值达到30%后抗风蚀作用明显减弱；3) RWEQ模型中各因子对于Qmax值的耦合作用、以及不同分蚀阶段的主导因素不同。低阈值阶段，土壤粘粒含量对于Qmax值的影响较明显；高阈值阶段，植被盖度又对Qmax值的影响较为明显。

Abstract: The RWEQ model is a key model for the quantitative study of soil wind erosion. In order to deeply analyze the relationship between each introduced variable and soil wind erosion in the modelling process of this model, the maximum soil transfer capacity (Qmax) was used as the descriptive variable to investigate the relationship between vegetation cover, soil clay content and Qmax. 9898 sets of variable combinations were generated by assigning values to vegetation cover and soil clay content in segments, and calculating the Qmax values under the preconditions of meteorological factor of 17, erodibility factor of 0.456, soil roughness factor of 0.68 and organic matter content of 2%. The relationship between the three is analysed for various combinations of conditions. The results show that: 1) There is a significant negative correlation between Qmax and vegetation cover, and 40% vegetation cover is an important node cover to inhibit wind erosion, and vegetation has strong resistance to wind erosion before reaching this cover; 2) As in the above method, the soil clay content is also negatively correlated with the Qmax value, and the wind erosion resistance is significantly weakened after the soil clay content threshold reaches 30%; 3) The coupling effect of each factor in the RWEQ model on the Qmax value, as well as the dominant factors in different erosion stages, is different. In the low threshold stage, the influence of soil clay content on Qmax values is more obvious; in the high threshold stage, the influence of vegetation cover on Qmax values is more obvious.

1. 引言

风力侵蚀是土壤侵蚀的主要类型之一，是荒漠化发生的首要环节 [1] 。风蚀会使土壤表层养分、有机质流失，土壤生产力下降，影响作物的生长；同时也会产生大量的粉尘及风沙问题，影响人类健康及正常的生产活动。土壤风蚀预报模型是解决风蚀问题的必要技术，侵蚀量及侵蚀速度是国家水土保持工作的重要依据 [2] 。其中RWEQ模型将经验和过程结合起来，并充分考虑了土壤可蚀性、土壤结皮、土壤水分、地表粗糙度、植被覆盖度、气候因子等与土壤风蚀相关的因子，充分挖掘各因子与土壤风蚀模数的关系，有利于推动风蚀定量关系研究。

目前我国有关RWEQ模型的研究主要集中在两个方面：一是利用计算机将遥感影像、基础数据图层等带入该模型，对区域风蚀因素及风蚀量进行分析 [3] [4] [5] ；另一方面是结合实测数据或引入新的计算、分类方法，改进或修正RWEQ模型参数，使其模拟结果更适用于中国地区 [6] [7] [8] [9] 。虽然许多学者对该模型进行了研究和区域性推广，但其在中国风蚀研究中仍存在局限性。一方面该模型是以美国大平原为基础，模型中部分经验参数来源于当地风蚀环境，然而风蚀因素组合情况更是复杂多样，因此模拟结果存在地域性问题；其次，由于RWEQ模型涉及风速、土壤湿度、植被、土壤机械组成等众多因素，所需基础数据较多，存在数据难获取的情况，从而导致RWEQ模型在中国区域的推广存在局限性 [10] [11] ；另一方面，RWEQ模型研究主要集中在探究各个独立影响因子与风蚀量的关系，对影响因子间的耦合关系研究稍显不足。因此，本文借鉴程皓 [12] 等人的赋值法，在确定气象因子为17、可蚀性因子为0.456、土壤粗糙因子为0.68、有机质含量为2%的前提条件下，将一定数值范围内的植被盖度与土壤粘粒含量进行赋值与全排列，并计算出Qmax值，对模型中植被盖度、土壤粘粒含量与Qmax的关系进行解读，并深层次地分析了两因素的耦合作用，企图以更简便的方式探究风蚀程度与各风蚀因素的关系，以期为后其研究提供新思路。

2. 研究方法

本研究采用赋值法探究风蚀因素与风蚀程度的关系，以及因素之间的耦合关系。根据已有研究 [13] 可知各风蚀因子的适用范围即气象因子为0.02~62.53、土壤可蚀性因子为0.08~0.55、地表粗糙因子为0.19~1.00，土壤结皮因子为0.09~0.95，植被因子为0.01~1.00。因此，在确定气象因子为17.00、可蚀性因子为0.46、土壤粗糙因子为0.68、有机质含量为2%的前提条件下，利用EXCEL2019软件对植被盖度及土壤粘粒含量分别从0~100%、1%~98%进行组合，共计9898个组合，并通过EXCEL2019软件计算并分析不同组合情况下的土壤最大转移容量(Qmax)。其相关计算公式如下 [14] ：

$Q_{\max }=109.8\left(\text{WF}\cdot \text{EF}\cdot \text{SCF}\cdot \text{<msup> K <mo> ′ </mo> </msup>}\cdot \text{COG}\right)$ (1)

式中：Qmax为最大沙通量，Qmax是在气候因子WF，土壤可蚀性EF和结皮SCF，土壤粗糙度K′以及植被因子COG基础上估算而得到。

土壤结皮可减少可侵蚀颗粒的含量，削弱土壤颗粒的磨蚀作用，从而将沙丘有效固定，防止和减弱土壤风蚀。RWEQ模型中土壤结皮SCF计算公式：

$\text{SCF}=\frac{1}{1+0.0066\times {\text{cl}}^2+0.021\times {\text{OM}}^2}$ (2)

式中：cl为土壤粘粒含量(5.0%~39.3%)；OM为土壤有机质含量(0.32%~4.74%)。

植被的存在对防治土壤风蚀具有显著的效果，其不仅可以增加地表粗糙度，对颗粒运动起到阻碍作用，还可改良土壤结构，增加土壤微团聚体含量，稳固结皮，从而增大起沙风速，达到减轻风蚀的作用，其表征的公式为：

$\text{C}={\text{e}}^{-0.0438\text{SC}}$ (3)

式中：SC为植被覆盖度(无量纲)。

用EXCEL2019软件统计Qmax在不同植被盖度、土壤粘粒含量条件下的最大值和最小值以及各个Qmax值段的组合数。应用Origin2022软件绘制Qmax值与植被盖度、土壤粘粒含量的关系图，分析不同土壤粘粒含量下Qmax值随植被盖度变化的点线图，以及不同植被盖度下Qmax值随土壤粘粒含量变化的点线图。最后，利用EXCEL2019软件分析两因素之间的耦合关系。

3. 结果分析

计算结果显示，在确定某些因素为定值的前提条件下，构建了具有9898个变量组合的全排列数据集，数据集中所有整数组合的Qmax值小于531 kg/m，其中最小值为0.11245 kg/m，最大值为530.7128 kg/m，Qmax值小于7的组合占总数的一半以上。

3.1. 极端风蚀因素组合对于Qmax值的影响

研究发现，当植被盖度达到100%，土壤粘粒含量为98%时，Qmax值最小，为0.011245，表明在土壤中粘粒含量较高、植被覆盖率也较高的环境中，风蚀程度最小；而当植被盖度为0%，土壤粘粒含量为1%时，Qmax值为530.7128，表明当土壤中粘粒含量、无植被覆盖的环境中，土壤风蚀程度达到最大。虽然上述极端组合在在自然界中不常见，但仍有存在，如申陆等人 [15] 应用RWEQ模型分析了浑善达克沙地的极端风蚀环境下的土壤风蚀强度及风蚀影响因素。

3.2. Qmax值临界值与植被盖度、粘粒含量的关系

根据表1分析Qmax值不同分段与植被盖度、粘粒含量的百分比的关系可以发现，每个Qmax值分段与植被盖度临界值相对应。低Qmax值分段对应高植被盖度与粘粒含量；高Qmax值分段对应于低阈值植被盖度与粘粒含量，初步分析植被盖度与Qmax值呈现负相关，即植被盖度越高，Qmax值越小，土壤粘粒含量与Qmax值关系同上。

进一步研究发现，植被盖度较大时，Qmax值较小。当Qmax值小于1时，植被盖度均大于51%；而当植被盖度大于51%时，Qmax值均小于55 kg/m。植被盖度越小，Qmax值越大。当Qmax值大于400 kg/m时，植被盖度均小于6%；而当植被盖度小于6%时，Qmax值均大于7 kg/m。由此可见，植被盖度是导致Qmax值出现临界值必要不充分条件。

Table 1. Correspondence of Qmax values with vegetation cover and soil clay content thresholds

表1. Qmax值分段与植被盖度、土壤粘粒含量临界值对应

3.3. Qmax值和植被盖度的关系

根据图1，固定土壤粘粒含量为某一定值，分析植被盖度和Qmax值的关系发现，植被盖度和Qmax值呈负相关关系，当植被盖度低于40%时，植被盖度曲线斜率比Qmax值小，当植被盖度高于40%时，植被盖度曲线斜率比Qmax值曲线斜率大。此特征表明，植被盖度在达到40%以前，植被具有剧烈的抗风蚀作用，即随植被盖度的增加，土壤最大转移容量骤减；当植被盖度达到40%以后，风蚀作用基本被抑制，随植被盖度的增加，Qmax值降低的速率逐渐变缓。

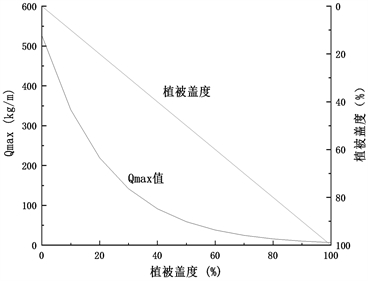(a) 土壤粘粒含量为1%时 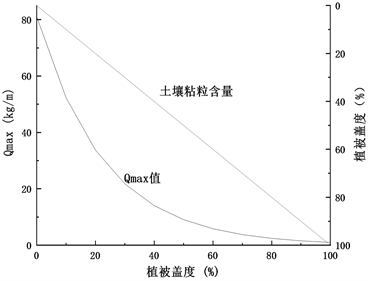(b) 土壤粘粒含量为30%时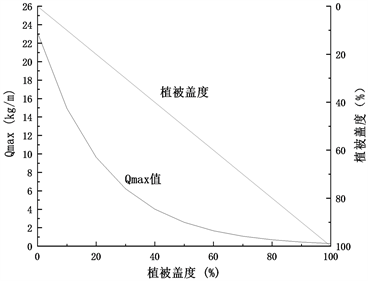(c) 土壤粘粒含量为60%时 (d) 土壤粘粒含量为90%时

Figure 1. Characteristics of the variation of Qmax values with vegetation cover

图1. Qmax值随植被盖度变化特征

3.4. Qmax值与土壤粘粒的关系

同上述方法相同，分析土壤粘粒含量和Qmax值的关系。根据图2分析可知，土壤粘粒含量和Qmax值呈负相关关系，且低粘粒含量对于Qmax值的影响较高粘粒含量明显，以植被盖度为0时为例，粘粒含量由1%增加至20%，Qmax值减少375.2897，但当粘粒到达70%时，对Qmax值的抑制作用减小，粘粒在70%~90%范围内时，Qmax值仅减小6.705228。从两条线的斜率来看，当土壤粘粒含量低于30%时，土壤粘粒曲线斜率比Qmax值小，当植被盖度高于30%时，土壤粘粒含量曲线斜率比Qmax值曲线斜率大。上述分析表明，土壤粘粒含量在30%以内变化时具有明显的抗风蚀作用，即随粘粒含量的增加，土壤最大转移容量骤减；当粘粒含量达到30%以后，风蚀作用基本被抑制，随粘粒含量的增加，Qmax值减小的速率逐渐变缓。

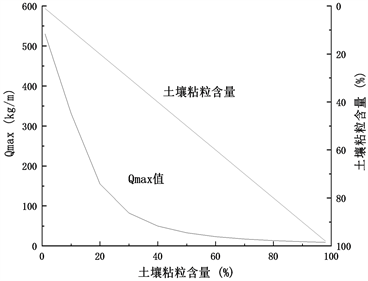(a) 植被盖度为0%时 (b) 植被盖度为30%时 (c) 植被盖度为60%时 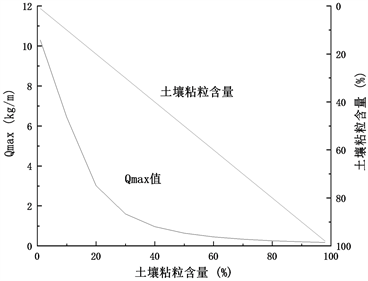(d) 植被盖度为90%时

Figure 2. Characteristics of the variation of Qmax values with soil clay content

图2. Qmax值随土壤粘粒含量变化特征

4. 耦合分析

假定上述植被盖度、土壤粘粒均与Qmax值呈现负相关关系正确，在已构建数据集中选取若干组合进一步探究三者的关系。分析表2可知，组合① ②中植被盖度升高、粘粒含量降低，Qmax值减小，当Qmax值趋势变化表现为追踪植被盖度时与上述结论相符，而当其趋势追踪土壤粘粒含量变化时违背上述结论；当粘粒含量为2%时，植被盖度只需达到4%，即可使Qmax值小于443，当植被盖度为2%时，粘粒含量只需达到5%，即可使Qmax值小于443。

同理分析组合① ③，植被盖度降低、粘粒含量增加，Qmax值变现为随土壤粘粒含量增加而减小、随植被盖度减小而减小，这显然同上述两者均与Qmax值呈现负相关的结论不符。分析出现此矛盾的原因是：一方面由于上述假设是在控制其余变量均为某一定值的前提下获得，然而在实际风蚀过程中，由于各风蚀因素的分布是不均匀、不连续，尤其植被、土壤颗粒等因素的分布具有较强随机性，几乎不存在如假设条件一般均匀变化的风蚀环境，然而，为了研究风蚀程度与各因素的关系，以往在实际研究中往往会忽视局部风蚀环境的细微差距，采用控制变量的方法进行分析；另一方面在风蚀过程中，各风蚀因素并不是完全孤立存在，而是存在耦合作用，如本文分析了植被盖度与粘粒含量对于Qmax值的影响存在耦合作用，所以当探究其中一方与Qmax值的关系时受到另一方条件的约束，从而导致两者与Qmax值的关系存在不确定性。表2即通过叠置变量的方法，从风蚀因素间相耦合的角度分析了三者的关系。

Table 2. Coupled analysis of vegetation cover and soil clay content

表2. 植被盖度、土壤粘粒含量耦合分析

进一步分析表2，组合① ②、① ③、④ ⑤、④ ⑥均存在两因素中一个降低1%、Qmax值降低50%左右的情况。但四组数据不同点在于：在各组合Qmax值均降低50%左右的前提下，① ②组合中粘粒降低1%，植被盖度需增加16%，而① ③组合中植被盖度降低1%时，粘粒含量仅增加了11%；④ ⑤当粘粒降低1%，植被盖度增加了14%，而④ ⑥组合中植被盖度降低1%，需增加28%的粘粒含量。以上分析意在说明，虽然植被盖度和土壤粘粒含量均影响Qmax值的大小，但显然两者对其影响程度不同。从低阈值分析，土壤粘粒含量对于Qmax值的影响较明显；而从高阈值分析，植被盖度又对Qmax值的影响较为明显，与前人所得结论相似 [16] 。这再一次验证了RWEQ模型中各因子对于Qmax值的耦合作用、以及不同风蚀阶段的主导因素不同。然而，从实际意义出发，在防风蚀工作中增加区域土壤中的粘粒含量较提高植被盖度困难，且增加植被是改变土壤机械组成、增加土壤团聚体结构的重要措施，因此改变区域植被覆盖率仍是风蚀工作的重要内容。

5. 讨论

植物是影响风蚀的主要因素之一，植被具有降低风速、防风固沙等作用，一切覆盖在地表上的植被形式，均可对土壤风蚀危害进行不同程度的减缓。植被覆盖对土壤侵蚀影响的作用机理目前已有大量的研究，部分学者从实验的角度观测植被对土壤风蚀的抑制作用，还有一部分学者通过建立定量模型来描述两者的关系，此类定量模型多为植被盖度与风蚀输沙率的定量关系模型 [17] [18] [19] [20] 。比较典型的是Wasson和Nanninga [21] 基于两种思路建立的有植被覆盖下的风蚀输沙率模型：一种为植被通过降低地面风速来防治风蚀： $q=B{\left[uf\left(c\right)-ut\right]}^3$ ；一种为植被增大起沙风速来抑制风蚀： $q=B{\left[u-ut\cdot f\left(c\right)\right]}^3$ 。我国有学者 [22] 通过借鉴Wasson模型，建立了2种毛乌素植被覆盖率与输沙率之间的定量关系模型，并提出该沙地植被覆盖率在40~50%时可以有效控制风蚀。此类模型是在借鉴Bagnold输沙率公式的基础上通过风洞试验或是理论推导得出的植被影响风蚀输沙的推广公式，两种角度均可表明植被盖度与风蚀程度呈现负相关，与本文结论一致。但也有学者发现当盖度低于30%时，风蚀程度与植被盖度呈现正相关；而盖度高于30%时，两者呈现负相关 [23] [24] 。风蚀作用的发生需要多因素的耦合作用，植被仅为风蚀因子中的一部分，因此不可能完全地将其从风蚀作用中剥离、单独研究其与风蚀的关系，即植被盖度对于风蚀程度的抑制作用受其他风蚀因素的影响，如本文中土壤粘粒含量影响植被与风蚀程度的关系。由于篇幅原因，本文仅对植被盖度、土壤结皮因子中的土壤粘土含量与Qmax的关系进行分析，后续将继续对其他风蚀因素展开研究。

RWEQ模型中土壤粘粒含量同时出现在土壤结皮因子与土壤可蚀性因子中，表明风蚀各要素是互相影响的，但是对于研究单个因素的影响存在限制。本文仅选取土壤结皮因子中粘粒的含量来研究其与风蚀的关系，存在不确定性。且由于目前对土壤分级的标准不尽相同，RWEQ模型使用的土壤质地分类系统为美国制，而中国采用的是国际制，因此笼统的带入公式是不可取的，对于土壤质地的转换还有待进一步研究。

6. 结论

本文利用赋值法，以更简便的方式探究了各种风蚀因素组合状况下风蚀程度与风蚀因素的关系，以及风蚀因素的耦合作用，具体结论如下：

1) Qmax值与植被盖度存在较明显的负相关关系，且40%是抑制风蚀作用的重要节点盖度。当植被盖度低于40%时，植被盖度曲线斜率大于Qmax曲线斜率，当植被盖度高于40%时，植被盖度曲线斜率小于其曲线斜率。表明在达到40%盖度前，增加植被盖度，Qmax值大幅度降低，即植被存在剧烈的抗风蚀作用，后期降幅较小。因此，在实际风固沙工作中可以此盖度为参考，合理安排区域植被盖度。

2) 土壤粘粒含量和Qmax值呈负相关关系，30%是抗风蚀作用的重要节点含量。土壤粘粒含量在达到30%前，具有剧烈的抗风蚀作用，但其含量在30%后，Qmax值降低速率逐渐减小。此结论启发我们在水土保持工作中，可通过增加土壤粘粒含量来提高土壤的抗风蚀能力，但为节约资源，可以30%为参考，合理增加土壤粘粒含量。

3) RWEQ模型中各因子对于Qmax值的耦合作用、以及不同风蚀阶段的主导因素不同。仅以植被盖度、粘粒含量为变量分析Qmax值的值域，从低阈值分析，土壤粘粒含量对于Qmax值的影响较明显；而从高阈值分析，植被盖度又对Qmax值的影响较为明显。此结论表明，在弱风蚀区可主要通过增加土壤粘粒含量的方式提高土壤抗风蚀能力，而在强风蚀地区可采用增加植被盖度的方式减弱风蚀作用。

基金项目

新疆水土保持监督管理项目(213031003)。