基于改进金豺优化算法的机器人路径规划

Robot Path Planning Based on Improved Golden Jackal Optimization Algorithm

摘要: 针对传统金豺优化算法GJO求解移动机器人路径规划RPP问题时存在寻优能力差，易陷入局部最优的缺点，本文提出一种改进的金豺优化算法IGJO。IGJO算法引入反向学习机制构建初始金豺种群，以提升初始解的质量；使用改进非线性能量逃逸因子，避免迭代后期过早收敛。同时，算法融合了个体记忆功能的精英反向学习策略搜索当前种群优秀解的反向空间，以增强算法的勘探能力。最后，IGJO对比5种优化算法的实验数据，实验结果表明，IGJO算法均优于其他对比算法。

Abstract: Aiming at the shortcomings of the traditional golden Jackal optimization algorithm GJO, such as poor optimization ability and easy to fall into local optimum when solving the RPP problem of mobile robot path planning, this paper proposes an improved golden Jackal optimization algorithm IGJO. IGJO algorithm introduced the opposition-based learning mechanism to construct the initial golden jackal population to improve the quality of the initial solution. The improved nonlinear energy escape factor was used to avoid premature convergence in the later iteration. At the same time, the elite opposition-based learning strategy integrated with individual memory function was used to search the reverse space of excellent solutions in the current population to enhance the exploration ability of the algorithm. Finally, IGJO compares the experimental data of five optimization algorithms. The experimental results show that IGJO algorithm is superior to other comparison algorithms.

1. 引言

机器人路径规划RPP (Robot Path Planning)就是在机器人事先知道目标相对位置的情况下，为机器人规划一条从起点到终点的最佳移动路径 [1] ，并且在移动的同时有能力避开环境中分散的障碍物，尽量减少路径长度，不与其发生碰撞，防止危险的发生。国内外就移动RPP问题展开了诸多研究，RPP方法可区分为三种方法分别为：传统算法、人工智能算法和智能搜索算法。传统路径规划包括人工势场法 [2] 、A*算法 [3] 等。人工智能算法包括Q-Learning [4] 和深度学习 [5] 。智能搜索算法主要包括蚁群算法(Ant Colony Optimization, ACO) [6] 、粒子群优化(Particle Swarm Optimization, PSO) [7] 、遗传算法(Genetic Algorithm, GA) [8] 等。传统算法的求解效率低，精度不足；人工智能算法在障碍物空间不完全可见或不稳定时，深度学习方法也不能很好地解决；Q学习方法无法在数据量较小的情况下进行高效的路径规划。虽然传统的元启发式算法可以有效地解决RPP问题，但是仍存在易陷入局部最优的问题。为此，研究学者着重于提高元启发式算法的寻优性能，采用多种改进策略提出众多算法。文献 [9] 提出一种双层改进蚁群算法提升了算法的收敛速度和平滑度；文献 [10] 提出了改进粒子群优化算法，实现多智能算法并行融合在路径搜索过程中具有快速和鲁棒性强的特点；文献 [11] 提出的改进遗传算法具有较快的收敛速度同时避免了局部最优，在多目标复杂环境下，能够得到合适的路径解。国内外还有许多学者对单一算法的缺陷进行了改进，比如改进人工鱼群算法 [12] 、改进人工蜂群算法 [13] 、改进灰狼算法 [14] 。

2022年Nitish Chopra和Muhammad Mohsin Ansari提出金豺优化算法 [15] (Golden Jackal Optimization, GJO)灵感来自金豺的协作狩猎行为。它们都经过数学建模和应用，通过与其他先进元启发式算法相比，寻优性能较好。针对高维复杂的优化问题，和其他算法一样仍存在一定程度上的停滞现象，造成算法寻优精度和效率低等。

鉴于此，为提高GJO算法的性能，本文提出IGJO算法。从以下方面进行改进：1) 在初始化阶段，IGJO采用反向学习方法构建初始种群，以提升解的质量；2) 在进化过程中，IGJO重新设置算法进行探索或开发的条件，更好的平衡算法的全局搜索与局部搜索能；3) 利用个体记忆功能的精英反向学习策略探索当前种群中精英个体的反向解空间，以增强算法的勘探能力。

本文其余内容组织如下：在第1节中，给出移动机器人路径规划环境模型，以及路径评价函数；在第2节中，介绍了原始金豺优化算法；在第3节中，介绍改进金豺优化算法；在第4节中，将IGJO与其他求解移动机器人避障路径规划的算法进行比较并分析结果；在第5节中，对本文进行总结。

2. 移动机器人路径规划

2.1. 环境模型

路径规划的环境建模方法有很多，如栅格法、拓扑图法等。栅格法 [16] 因其结构简单，信息量少，可以有效降低计算量，所以得到广泛应用。因此，本文采用栅格法构建环境模型。

栅格地图建立方式如图1所示。在栅格地图中用0表示黑色障碍物，用1表示自由栅格即可行区域。为方便仿真实验进行，假设所有栅格地图都为考虑机器人安全距离后扩展的环境，同时假设移动机器人为一质点，避免影响验证算法性能。

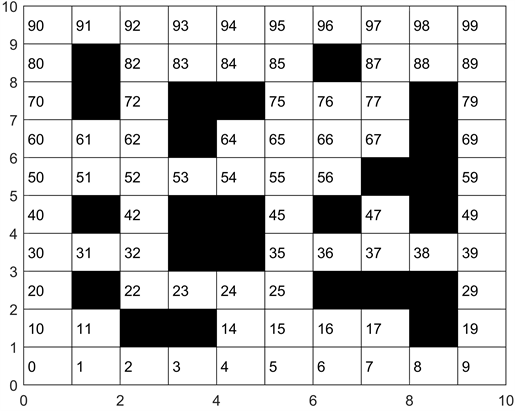
Figure 1. A raster map with an ordinal number

图1. 标记序号的栅格地图

在工作空间模型中，栅格坐标为栅格中心点的坐标，根据栅格坐标，按照从左到右、从上到下的顺序，对环境地图内的栅格依次编号，每个栅格的编号与行、列之间的关系为：

$\{\begin{array}{l}{x}_i=\mathrm{mod}\left(i,row\right)+1\\ y_i=\text{fix}\left(\frac{i}{col}\right)+1\end{array}$ (1)

其中： $\left(x_i,y_i\right)$ 为栅格的直接坐标；i为栅格的序号，row和col分别为栅格模型的行数和列数；mod为取余函数；fix为向上取整函数。通过编号可以计算出每个栅格的位置编号，从而确定自由栅格和障碍栅格所在的位置编号。

2.2. 路径评价函数

可将机器人的路径规划转换为在栅格地图中寻找初始位置运动到目标位置经过点集合的问题。假设S是机器人的初始位置，E是目标位置，算法为机器人规划出一条路径为： $\left[S,x_1,x_2,\cdots ,x_d,E\right]$ ，其中 $x_1,x_2,\cdots ,x_d$ 为机器人在栅格地图中运动时经过的点，且任意一点均处于可行域空间，相邻两点连线之间不存在障碍点。将机器人运动过程中的路径长度作为适应度函数，数学表达式如下：

$f\left(X\right)={\displaystyle {\sum }_{i=1}^{n-1}\sqrt{{\left(x_{i+1}-x_i\right)}^2+{\left(y_{i+1}-y_i\right)}^2}}$ (2)

式中， $x_i$ 和 $y_i$ 分别为机器人在栅格地图当前位置的横坐标和纵坐标， $x_{i+1}$ 和 $y_{i+1}$ 分别为机器人移动到下一个位置的横坐标和纵坐标，n为机器人运动过程中经历的节点总数。

3. 金豺优化算法

金豺算法是由Nitish Chopra和Muhammad Mohsin Ansari提出的一种群体智能算法；它模仿了自然界中金豺的狩猎行为。金豺通常与雄性和雌性一起捕猎。算法分为勘探和开发两个阶段；在这两个阶段中，金豺根据猎物的逃逸能力E，确定选择执行勘探阶段还是执行开发阶段。下面针对优化问题 $\min f\left(X\right)\left(X\in \left[lb,ub\right]\right)$ 介绍GJO的原理。在GJO中，猎物的逃逸能量记为E，其计算公式为

$E=E_1\ast E_0$ (3)

其中，E₁表示猎物逃跑能量呈现递减状态，E₀为猎物初始的逃跑能量。计算公式如下：

$E_0=2\ast r-1$ (4)

$E_1=c_1\ast \left(1-t/T\right)$ (5)

式中：r为[0, 1]范围内的随机数；t为当前GJO的迭代次数；T为最大迭代次数；c₁为一个常数值，取值为1.5。在整个迭代过程中，E₁从1.5线性递减到0。下面分别对这两个阶段介绍。

3.1. 勘探阶段

当逃逸能量 $\left|E\right|\ge 1$ 时，算法进入勘探阶段，进行广泛的搜索操作。位置更新公式为

$Y_1\left(t\right)=Y_M\left(t\right)-E\ast \left|Y_M\left(t\right)-rl\ast Prey\left(t\right)\right|$ (6)

$Y_2\left(t\right)=Y_{FM}\left(t\right)-E\ast \left|Y_{FM}\left(t\right)-rl\ast Prey\left(t\right)\right|$ (7)

其中： $Prey\left(t\right)$ 为第t次迭代的猎物的位置； $Y_M\left(t\right)$ 和 $Y_{FM}\left(t\right)$ 分别为第t次迭代的雄性豺狼和雌性豺狼的位置； $Y_1\left(t\right)$ 和 $Y_2\left(t\right)$ 分别为第t次迭代的猎物相应的雄性豺狼和雌性豺狼更新后的位置。在公式(6)和(7)中，rl表示一个基于莱维分布的随机数，可用如下公式计算：

$rl=0.05\ast LF\left(y\right)$ (8)

$LF\left(\right)$ 是莱维飞行函数，其计算方法如下：

$LF\left(y\right)=0.01\ast \left(\mu \ast \sigma \right)/\left|v^{1/\beta }\right|$ (9)

$\sigma =\Gamma \left(1+\beta \right)\ast \sin \left(\frac{\pi \beta }{2}\right)/{\left(\Gamma \left(\frac{1+\beta }{2}\right)\ast \beta \ast 2^{\left(\beta -1\right)/2}\right)}^{1/\beta }$ (10)

式中： $\mu$ 、v是(0, 1)范围内的随机数； $\beta$ 为默认常数，设置为1.5； $\Gamma$ 为伽马函数。

3.2. 开发阶段

当逃逸能量 $\left|E\right|<1$ 时，算法进入开发阶段，进行精细的局部搜索。位置更新公式为：

$Y_1\left(t\right)=Y_M\left(t\right)-E\ast \left|rl\ast Y_M\left(t\right)-Prey\left(t\right)\right|$ (11)

$Y_2\left(t\right)=Y_{FM}\left(t\right)-E\ast \left|rl\ast Y_{FM}\left(t\right)-Prey\left(t\right)\right|$ (12)

其中： $Prey\left(t\right)$ 为第t次迭代的猎物的位置； $Y_M\left(t\right)$ 和 $Y_{FM}\left(t\right)$ 分别为第t次迭代的雄性豺狼和雌性豺狼的位置； $Y_1\left(t\right)$ 和 $Y_2\left(t\right)$ 分别为第t次迭代的猎物相应的雄性豺狼和雌性豺狼更新后的位置。综上，金豺的位置更新公式如(13)：

$Y\left(t+1\right)=\left(Y_1\left(t\right)+Y_2\left(t\right)\right)/2$ (13)

其中： $Y\left(t+1\right)$ 为第 $t+1$ 次迭代后金豺的位置。

4. 改进金豺优化算法

本文借助反向学习机制和融合个体历史信息的方法构筑改进金豺优化算法。首先在初始化阶段，改进金豺算法采用反向学习方法构建初始种群，力求提升解的质量；其次在进化过程中，重新设置算法进行探索或开发的条件，更好的平衡算法的全局搜索与局部搜索能；最后利用粒子群算法中的个体记忆功能的精英反向学习策略探索当前种群中历史最优个体的反向解空间，力求增强算法的勘探能力。

4.1. 初始化种群

为提升金豺种群初始解的质量，改进金豺算法采用四邻域搜索和反向学习 [17] 策略初始化种群，主要包括以下步骤。

1) 根据栅格模型的选择大小固定的栅格。初始路径的生成通过每行中随机选择一个自由栅格构成起点到终点的必经节点，生成一条从起点到终点的间断路径。

2) 将每行随机选择的路径点连接成一条无间断的连续路径。首先判断相邻的两点是否连续，判断方法为：

$D=\max \left(abs\left(x_{i+1}-x_i\right),abs\left(y_{i+1}-y_i\right)\right)$ (14)

如果 $D<1$ 说明相邻的路径节点连续，反之不连续。针对不连续的节点通过计算中点进行插入操作，具体操作如下：

$\{\begin{array}{l}{x}_{insert}=\text{floor}\left(\frac{x_i+x_{i+1}}{2}\right)\\ y_{insert}=\text{floor}\left(\frac{y_i+y_{i+1}}{2}\right)\end{array}$ (15)

其中，floor函数表示向下取整。

3) 如果插入节点为障碍物点，则对该障碍物点采用四邻域搜索见图2即上、下、左、右四个方向进行搜索，四邻域搜索相比八邻域搜索减少搜索过程，同时可以有效避免斜穿障碍物的现象。通过四邻域搜索策略判断周围四个方向是否为自由栅格，如果为自由栅格则插入，否则该路径无效。重复以上步骤直至该路径上前后两个节点依次连续。路径可表示为：

$X_I=\left|S,x_1,x_2,\cdots ,x_{i-1},x_i,x_{i+1},\cdots ,x_d,E\right|$

4) 根据生成的路径对每一个解构建反向解，各维度的取值范围为 $\left[X_d^l,X_d^u\right]$ ， $X_d^l$ 和 $X_d^u$ 分别表示第d维取值的最小值和最大值。反向解构建如下：

$X_{id}^o=r\left(X_d^l+X_d^u\right)-X_{id}$ (16)

5) 根据生成的初始解和反向解进行评价，通过路径评价函数从2N个个体选取前N个最优目标构成初始种群。

Figure 2. Four domain diagram

图2. 四领域图

4.2. 非线性能量因子更新策略

在基本GJO算法中，利用逃逸能量E控制算法在迭代过程中由全局搜索到局部搜索，当逃逸能量 $\left|E\right|\ge 1$ 时，算法进行全局搜索，当逃逸能量 $\left|E\right|<1$ 时，算法进行局部搜索。E₁从1.5线性递减到0，这会导致算法迭代后期陷入局部搜索。本文提出一种非线性能量因子E₁的更新方式，使算法在迭代后期进行局部搜索的同时也保留了算法进行全局搜索的可能。能量因子E₁更新公式如下：

$E_1=c_1\ast {\left(1-t/T\right)}^{\alpha }$ (17)

$E=E_1\ast E_0$ (18)

$\alpha$ 在本文取值为4。图3和图4分别展示了迭代次数 $T=300$ 时能量因子E₁和逃逸能力因子E的变化曲线。

从图3可知，改进后的E₁在算法前期下降缓慢，有利于算法初期进行全局搜索，避免早熟现象；在算法后期加快递减速度，提高了算法的后期局部搜索的能力，使得改进金豺算法在整个迭代过程中平衡了勘探和开发。

Figure 3. E₁ change curve

图3. E₁变化曲线

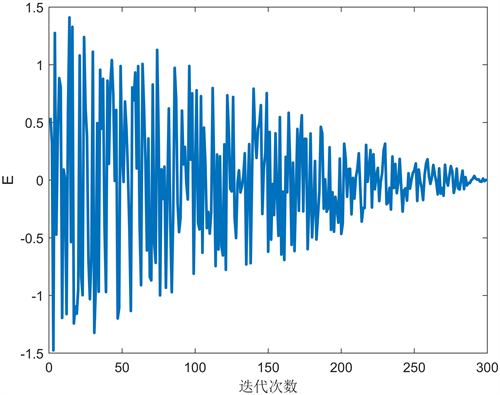(a) 改进前逃逸能量因子E变化曲线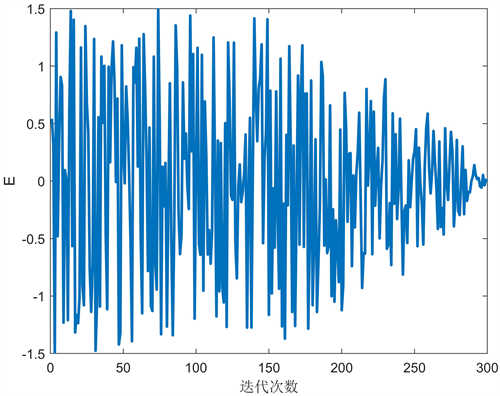(b) 改进后逃逸能量因子E变化曲线

Figure 4. Change curve of escape energy factor E before and after improvement

图4. 改进前后逃逸能量因子E变化曲线

4.3. 融合历史信息的精英反向学习策略

该策略利用精英个体比一般个体包含更多有效信息的这一特点，通过精英个体构造出反向种群以此来增加种群的多样性。为此，本文利用个体历史最优来构建精英反向种群，在每次迭代中，改进金豺算法首先根据更新后的种群来更新每个个体的历史最优位置信息，随后选取前50%的金豺个体历史最优位置信息构建精英种群 $X_i^E$ 。反向解定义为：在D维空间中，假设种群中可行解是 $X_{id}$ ，那么它的反向解 ${X^{\prime }}_{id}$ 为：

${X^{\prime }}_{id}=r\left(l{b}_d+u{b}_d\right)-X_{id}$ (19)

其中， $d=1,2,\cdots ,D$ ； $X_{id}$ 表示当前种群解向量 $X_i$ 在d维的取值， ${X^{\prime }}_{id}$ 表示当前反向种群解向量 ${X^{\prime }}_i$ 在d维的取值， $l{b}_j=\min \left\{X_{i,j}\right\}$ $u{b}_j=\max \left\{X_{i,j}\right\}$ ，r是 $\left[0,1\right]$ 上的随机数。根据反向解的定义生成 $X_i^E$ 的反向种群 ${X^{\prime }}_i$ ，选取混合种群 $X_i^E\cup {X^{\prime }}_i$ 中前50%的优秀解代替更新后最差的个体进入下一次的迭代，以提升算法的性能。

4.4. 删除操作

删除操作可有效减少路径节点数量，可最大限度优化目标函数同时使路径更加平滑，通过删除操作实现去除冗余路径节点的前后路径效果对比图见图5，蓝色表示删除前的路径，红色表示删除操作后的路径。删除操作通过判断连续路径上相邻三个节点中的中间节点的相邻路径节点之间直线连接有无障碍物，来判断中间节点是否为冗余节点。依次循环遍历三个节点的中间节点相邻节点直接相连的路径节点是否无障碍物，若无障碍物，则删除三个相邻节点的中间节点；若相邻节点的连线上有障碍物，则判断下一个节点开始的三个相邻节点的中间节点的前后节点直接相连是否有障碍物；依次循环直到倒数第二个节点。

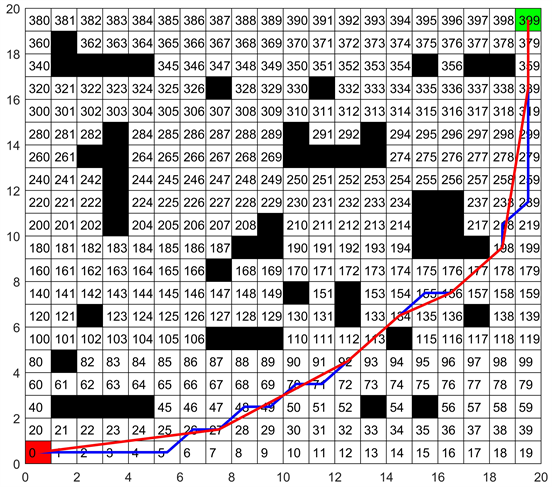
Figure 5. Path comparison before and after deletion

图5. 删除前后路径对比

举例来说，在图5的栅格模型中，假设编号239的位置，编号239的前一路径节点为编号218，下一个路径节点为编号339，此时从编号218到编号339的路径长度为6.4142；经过删除操作后，编号239的相邻节点即前一路径节点和后一节点之间无障碍物故可直接相连，此时从编号218到编号339的路径长度为6.0828，路径长度缩短了0.3314，并使得路径更加趋于平滑。

4.5. 本文算法流程

本文算法步骤具体如下：

步骤1：环境建模：采用栅格图进行建模，确定机器人的起点和终点位置。

步骤2：初始化：利用反向学习初始化种群，并计算金豺种群的适应度值。

步骤3：种群排序：根据排序结果选取适应度最高的2只金豺分别为雄性金豺和雌性金豺。

步骤4：计算能量因子：通过改进的逃逸能量公式(17)计算逃逸能量因子E，根据逃逸能量选择不同的策略。

步骤5：种群进化：根据式(6)~式(13)更新金豺位置。

步骤6：精英反向搜索：采用精英反向学习策略更新种群。

步骤7：终止条件判断：若满足终止条件，停止迭代并显示最优适应度值和最优位置；否则，转步骤3。

5. 实验仿真及结果分析

本文所有计算在配置为Intel(R) Core(TM) i7-11800H CPU @ 2.30GHz 2.30 16GB RAM的微型计算机上进行，操作系统为Microsoft Windows11。利用MATLAB R2021a仿真环境下进行分析实验。

5.1. 环境模型设置与算法参数

分别在20 × 20的简单环境和复杂环境两种不同环境的栅格环境下，与传统PSO、GJO、GA、ACO、ACO_GA和原始GJO算法进行仿真对比实验。为了避免随机性对结果的影响，分别将六种算法独立运行20次。实验中，六中算法种群规模为50，每次实验迭代100次，以及相同的环境模型、起点、终点。GA交叉概率为0.8，变异概率为0.2；PSO加速因子 $c_1$ 、 $c_2$ 设置为1，速度最大值 $\text{V}\max =-20$ ，最小值 $\text{V}\min =-20$ ；ACO信息素初始值 ${\tau }_0=1$ ，信息素启发因子 $\alpha =2$ ，期望启发因子 $\beta =6$ ，信息素挥发因子 $\rho =0.1$ ，信息素增强系数 $Q=10$ 。

5.2. IGJO与其他算法的比较

本节中，分别对IGJO与其他5个算法求解RPP的计算结果进行比较和分析。在表1和表2中给出各算法的求解结果。在简单环境下，设置36障碍物，红色表示起始点，绿色表示目标点。实验结果如图6、图8(a)和表1所示。在复杂环境下，设置76障碍物，红色表示起始点，绿色表示目标点。实验结果如图7、图8(b)和表2所示。

Table 1. Experimental results of six algorithms on 20 × 20 simple maps

表1. 六种算法在20 × 20简单地图实验结果

(a) PSO (b) GA (c) ACO (d) ACO_GA (e) GJO (f) IGJO

Figure 6. Path planning of six algorithms in a 20 × 20 simple map

图6. 六种算法在20 × 20简单地图中的路径规划

(a) PSO (b) GA (c) ACO (d) ACO_GA (e) GJO (f) IGJO

Figure 7. Path planning of six algorithms in a 20 × 20 complex map

图7. 六种算法在20 × 20复杂地图中的路径规划

(a) 简单地图 (b) 复杂地图

Figure 8. Iterative process of six algorithms in 20 × 20 map

图8. 六种算法在20 × 20地图中的迭代过程

Table 2. Experimental results of six algorithms on 20 × 20 complex maps

表2. 六种算法在20 × 20 复杂地图实验结果

首次将GJO算法用于求解机器人避障路径规划问题，图6~8、表1和表2证明了GJO算法同PSO、GA、ACO、ACO_GA算法一样，可以应用与移动机器人避障路径规划问题，证明了GJO算法在移动机器人路径规划的可行性，为路径规划领域提供了一种新方法。

通过表1和表2的路径长度标准差可以看出传统GJO算法在求解移动机器人避障路径规划问题的稳定性不高，进而改进的GJO算法的更新因子来平衡全局搜索和局部搜索能力之间的平衡，改进GJO算法在前期提高了全局搜索能力，使算法在求解移动机器人避障路径规划时不易陷入局部极值，在后期提高了局部搜索能力，加快了收敛速度，提高了算法的稳定性。通过表1和表2可以看出改进GJO算法最短路径、平均路径长度、最长路径相比其他算法都是最优。与此同时，图8中(a)和(b)给出了六种算法在两种测试环境中的最优进化曲线，据此可知，反向学习初始化方法使得改进GJO算法在初期能够获得高质量的解，而融合了历史最优的精英反向学习策略增强了算法的勘探能力，克服了传统GJO算法易陷入局部最优的不足。综上所述，本文提出的改进金豺优化算法应用路径规划中在最短路径、最长路径和平均路径均取得最优效果。

6. 总结与展望

本文提出一种IGJO算法的机器人路径规划研究方法。首先在初始化阶段，IGJO算法采用反向学习方法构建初始种群，力求提升解的质量；其次在进化过程中，重新设置算法进行探索或开发的条件，更好的平衡算法的全局搜索与局部搜索能；最后采用个体记忆功的精英反向学习策略探索当前种群中反向解空间，以增强算法的勘探能力。最后通过删除操作，去除冗余节点，平滑路径。在MATLAB软件中进行了仿真实验，结果表明，本文改进算法的最优解、最差解和平均解都优于对比算法，证明了改进GJO算法的可行性和有效性，为研究移动机器人避障路径规划提供了重要参考价值。但是，本文改进算法的速度有待进一步提高，同时只适用于静态全局路径规划，后续可以通过与实时动态局部路径规划结合，完善本文算法。