自然数的平方和公式推导

The Formula Derivation of the Sum of Squares of Natural Numbers

摘要: 解题是数学学习的一个核心内容和一种最基本的活动形式。罗增儒教授曾指出“数学教育中真正发生数学的地方都无一例外地有数学解题活动”。因此数学教学应“以解决问题为导向”，解决问题的过程是学习新知识、发展智力和提高能力的过程，而“一题多解”恰恰是解题教学中最常用、最有效的一种教学手段与技术。本文针对解题灵活性的要求，通过“自然数的平方和公式推导”的一题多解，完善学生数学知识框架，提升思维的发散性和系统性。让学生感受到学习数学的乐趣，从而进一步提高学生数形结合能力以及代数运算的能力以及空间解析能力等，激发学生学习数学的兴趣。

Abstract: Problem solving is a core content and the most basic form of activity in mathematics learning. Professor Luo Zengru once pointed out that “all places where mathematics truly occurs in mathe-matics education have mathematical problem-solving activities”. Therefore, mathematics teaching should be “problem-solving oriented”. The process of problem-solving is the process of learning new knowledge, developing intelligence, and improving abilities. “Multiple solutions to one problem” is precisely the most commonly used and effective teaching method and technique in problem-solving teaching. In view of the requirement of flexibility in solving problems, this paper improves students’ mathematical knowledge framework, improves their divergent and systematic thinking, makes students feel the fun of learning mathematics, and further improves students’ ability to combine numbers with shapes, algebraic operations and spatial analysis, and stimulates students’ interest in learning mathematics through multiple solutions to one problem of “square sum formula derivation of natural numbers”.

1. 引言

美国著名数学教育家、波利亚先生指出：“若一位认真备课的教师能够提出一道有意义但不复杂的数学问题，那么学生便可以通过这道题，如同通过一扇门，进入一个完整的理论领域，去探究问题的不同方面。”对于一个数学问题，从不同的角度去思考，总是会有不同的解法，而这些解法也同样能够暴露出数学知识之间的关联性 [1] 。因此，在高中数学教学中，应当重视教授解题技巧和方法，以帮助学生更好地理解所学知识，并将其应用于实际生活中。

对于“自然数的平方和公式”(即： $1^2+2^2+3^2+\cdots +n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$ )的推导证明，高中课本上仅

仅给出了数学归纳法的证明方法，导致很多学生对于该公式的本质并没有理解，在解题中只能局限于一种方法，不能做到科学地归纳和分类，往往以传统的解题思路来做答，无法做到举一反三、触类旁通。

随着新课程改革的不断深入，这就要求学生不能仅仅局限于用传统方法来解决数学问题，因而为了提高学生的数学学习效率，必须不断地创新和改革传统的解题方法 [2] 。本文将分别从代数、高等数学以及解析几何的角度出发，介绍几种推导自然数平方和公式的方法。

2. 自然数平方和公式推导

2.1. 代数方法

方法一：数学归纳法

数学归纳法是一种特殊的直接证明的方法，是连接有穷与无穷间的桥梁之一，一些与正整数n (n取无限多个值)有关的数学命题，几乎都可以通过数学归纳法进行证明 [3] 。在高中阶段就学过数学归纳法，通过数学归纳法我们证明了等差数列和等比数列的通项公式，其本质是通过经验，观察，推理，验证当公式对 $n,\left(n-\text{1}\right),\left(n-\text{2}\right),\cdots ,\text{1}$ ，即n取任意数的时候都成立时，则公式成立，证明了公式的正确性和从特殊性到一般性，蕴含了极限的数学思想。

通过观察1²，2²，3²，4²的结果，会发现它们均满足 $\frac{n\left(n+1\right)\left(2n+1\right)}{6}$ ，这就启发我们利用数学归纳法对这个命题进行严格证明。

首先对于前n个自然数的平方和，若给出命题：

$1^2+2^2+3^2+4^2+\cdots +n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$ ，

下面用数学归纳法做出证明：

① 当 $n=1$ 时，上式左边 $=1^2=1$ ，右边 $=\frac{1\times 2\times 3}{6}=1$ ，左 = 右，命题正确。

② 假设 $n=k\left(k\in N^{+}\right)$ 时命题正确，即：

$1^2+2^2+3^2+4^2+\cdots +k^2=\frac{1}{6}k\left(k+1\right)\left(2k+1\right)$ ，那么

$\begin{array}{c}{1}^2+2^2+3^2+4^2+\cdots +k^2+{\left(k+1\right)}^2=\frac{1}{6}k\left(k+1\right)\left(2k+1\right)+{\left(k+1\right)}^2\\ =\frac{1}{6}\left(k+1\right)\left[k\left(2k+1\right)+6\left(k+1\right)\right]\\ =\frac{1}{6}\left(k+1\right)\left(2k^2+7k+6\right)\\ =\frac{1}{6}\left(k+1\right)\left(k+2\right)\left(2k+3\right)\\ =\frac{1}{6}\left(k+1\right)\left[\left(k+1\right)+1\right]\left[2\left(k+1\right)+1\right]\end{array}$

即当 $n=k+1$ 时命题也成立

所以原命题对于任意自然数均成立，即

$1^2+2^2+3^2+4^2+\cdots +n^2=\frac{1}{6}n\left(n+1\right)\left(2n+1\right)$

数学归纳法所蕴含的就是数学思想中的极限思想，通过方法一的学习，可以加深学生从具体到抽象，由特殊到一般的认识规律的认识，发展学生的逻辑思维能力。

方法二：组合数累加法

组合计数是数学中的一个分支，主要研究将多个事物进行组合的方法和技巧 [4] 。在高中数学数列求和经常用到组合数累加法，而数列问题大多是与自然数有关，因此不难猜想，累加法同样也可以用于计算自然数平方的和。在现实生活和学术研究中，组合计数是非常重要的。从m个不同元素中取出n (n ≤ m)个元素的所有组合的个数，叫做从m个不同元素中取出n个元素的组合数。

这里先列出排列组合的主要关系式：

排列数公式： $A_n^m=\frac{n!}{\left(n-m\right)!}$ ①

组合数公式： $C_n^m=\frac{n!}{m!\left(m-n\right)!}$ ②

即 $A_n^m=C_n^m{A}_n^m$ ③ $C_n^m=C_n^{n-m}$ ④ $C_n^m+C_n^{m-1}=C_{n+1}^m$ ⑤

上述式中 $m<n$ ，其中 $m,n$ 都是自然数。

则根据排列数公式，我们可以利用这些公式对 $n^2$ 进行适当的分解。易得：

$\begin{array}{l}{A}_2^2+A_3^2+A_4^2+A_5^2+\cdots +A_{n+1}^2\\ =1\times 2+2\times 3+3\times 4+4\times 5+\cdots +n\left(n+1\right)\\ =\left(1+1^2\right)+\left(2+2^2\right)+\left(3+3^2\right)+\left(4+4^2\right)+\left(5+5^2\right)+\cdots +\left(n+n^2\right)\\ =1^2+2^2+3^2+4^2+\cdots +n^2+1+2+3+4+\cdots +n\end{array}$

因为 $A_2^2+A_3^2+A_4^2+A_5^2+\cdots +A_{n+1}^2=A_2^2\left(C_2^2+C_3^2+C_4^2+C_5^2+\cdots +C_{n+1}^2\right)$

根据组合数性质，得

$C_2^2+C_3^2+C_4^2+C_5^2+\cdots +C_{n+1}^2=C_{n+2}^3$

所以

$\begin{array}{c}{A}_2^2+A_3^2+A_4^2+A_5^2+\cdots +A_{n+1}^2=A_2^2{C}_{n+2}^3\\ =2\times 1\times \frac{\left(n+2\right)\times \left(n+1\right)\times n}{3\times 2\times 1}\\ =\frac{\left(n+2\right)\left(n+1\right)n}{3}\end{array}$

根据以上运算，可以得到

$\begin{array}{c}{1}^2+2^2+3^2+4^2+\cdots +n^2=A_2^2+A_3^2+A_4^2+A_5^2+\cdots +A_{n+1}^2-\left(1+2+3+4+\cdots +n\right)\\ =\frac{\left(n+2\right)\left(n+1\right)n}{3}-\frac{n\times \left(n+1\right)}{2}\\ =\frac{n\left(n+1\right)\left(2n+1\right)}{6}\end{array}$

此外我们还可以利用杨辉三角的规律。

首先我们先来观察一下如图1所示的杨辉三角。我们可以发现每相邻两行的第三个数之和都是自然数的平方。例如：第3行的第三个数为3，第4行的第三个数为6，则两数之和9为即为3²。

Figure 1. Pascal’s triangle

图1. 杨辉三角

此外组合数有一个重要的性质即 $C_n^{m+1}+C_n^m=C_{n+1}^{m+1}$ (其中：组合数 $C_n^m$ 中当 $n<m$ 时，则 $C_n^m=0$ )

因此我们可以得到：

$1^2=C_1^2+C_2^2$ ， $2^2=C_2^2+C_3^2$ ， $3^2=C_3^2+C_4^2$ ， $\cdots$ ， $n^2=C_n^2+C_{n+1}^2$

则自然数的平方和可用下式表示：

$\begin{array}{c}{1}^2+2^2+3^2+\cdots +n^2=C_1^2+C_2^2+C_2^2+C_3^2+C_3^2+C_4^2+\cdots +C_n^2+C_{n+1}^2\\ =\left(C_1^2+C_2^2+C_3^2+C_4^2+\cdots +C_n^2\right)+\left(C_2^2+C_3^2+C_4^2+C_5^2+\cdots +C_{n+1}^2\right)\\ =C_{n+1}^3+C_{n+2}^3\end{array}$

$\begin{array}{c}=\frac{n\left(n-1\right)\left(n+1\right)}{6}+\frac{n\left(n+1\right)\left(n+2\right)}{6}\\ =\frac{n\left(n+1\right)\left(2n+1\right)}{6}\end{array}$

组合数中的第二种方法不仅利用了组合数的性质，同时还利用了杨辉三角的特殊规律。使学生的思维能力以及运算能力都得到了提高，有利于形成和提高分析问题和解决问题的能力。

方法三：待定系数法

在解数学问题的过程中，有时候无法直接求出问题的答案，比如因式分解、求函数解析式等，如果已知所求结果具有某种确定的形式，则可引进一些尚待确定的系数来表示这种结果，即一种数学方法——待定系数法，建立某种等量关系，从而达到解决问题的目的。其本质是根据恒等条件列出一组含待定系数的方程，从而解方程或消去待定系数。

首先已知自然数的一次方幂和的结果是一个关于n的二次式，其次由不等式 $n^3>1^2+2^2+3^2+4^2+\cdots +n^2>\frac{n}{2}\cdot \frac{n}{2}>{\left(\frac{n}{2}-1\right)}^3$ ，因此我们可以猜想自然数的二次方幂和的结果是一个关于n的三次式，利用待定系数法求证。

将数列 $\left\{n^2\right\}$ 看成特殊的二阶等差数列。其中二阶等差数列的前n项和 $S_n=1^2+2^2+3^2+\cdots +n^2$ 是关于n的三次式。

设 $f\left(n\right)=1^2+2^2+3^2+\cdots +n^2=a{n}^3+b{n}^2+cn+d$ (其中 $a,b,c,d$ 为待定系数)

令 $n=1,2,3,4$ ，代入上式中分别得到：

$\{\begin{array}{l}a+b+c+d=1\\ 8a+4b+2c+d=5\\ 27a+9b+3c+d=14\\ 64a+16b+4c+d=30\end{array}$

解得 $a=\frac{1}{3}$ ， $b=\frac{1}{2}$ ， $c=\frac{1}{6}$ ， $d=0$

所以 $f(\left(n\right)=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

由此即可证得结论 $S_n=1^2+2^2+3^2+\cdots +n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

该方法相较于数学归纳法，计算量更小，它在知道答案的形式的前提下，将复杂的问题通过引入特定的系数，转化为较简单的问题。通过这个方法有助于提高学生的解题效率以及准确性。

2.2. 高等数学方法

人们常有一种片面的观点认为高等数学知识在中学数学教学中几乎无用 [5] 。其实高等数学知识在开阔中学教师的视野、指导中学数学解题等方面有很大的作用．下面就介绍几种应用高等数学的知识来解决该问题的方法。

方法一：积分法

我们先来了解一下积分所体现的思想就是无限求和，并且由于直接求解自然数的平方和较为复杂，但是我们知道自然数前n和为 $\frac{\left(1+n\right)n}{2}$ ，因此这就启发我们利用积分对所求的问题进行转换。通过设 $f\left(n\right)=2n$ ，则 ${\displaystyle \int f\left(n\right)\text{d}n}=n^2+C$ ，将求解自然数的平方和转化为求解

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \int f\left(i\right)\text{d}n}}$

我们可以得出

$\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{i}^2}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left({\displaystyle \int f\left(i\right)\text{d}n}-C\right)}+nC\\ =\left({\displaystyle \int {\displaystyle \underset{i=1}{\overset{n}{\sum }}f\left(n\right)}}\right)-nC+nC\\ =\left({\displaystyle \int 2{\displaystyle \underset{i=1}{\overset{n}{\sum }}i}\text{d}n}\right)-nC+nC\\ =\left({\displaystyle \int 2\cdot \frac{\left(1+n\right)n}{2}\text{d}n}\right)-nC+nC\\ =\left({\displaystyle \int \left(n^2+n\right)\text{d}n}\right)-nC+nC\\ =\frac{n^3}{3}+\frac{n^2}{2}+nC\end{array}$

通分得原式 $=\frac{2n^3+3n^2+6nC}{6}=\frac{n\left(2n^2+3n+6C\right)}{6}$

将 $n=1$ ，代入得：

$\frac{2+3+6C}{6}={\displaystyle \underset{i}{\overset{1}{\sum }}{i}^2}=1^2=1$

解得 $C=\frac{1}{6}$

则原式 $=\frac{n\left(2n^2+3n+1\right)}{6}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

方法二：阿贝尔变换求和法

阿贝尔变换可以用于求解能分解为数列积的数列的求和中。首先先来介绍阿贝尔(Abel)变换，并利用该方法来解决自然数的平方和的问题

令：

$S={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_k{b}_k}=a_1{b}_1+a_2{b}_2+a_3{b}_3+\cdots +a_n{b}_n$

$B_1=b_1,B_2=b_1+b_2,B_3=b_1+b_2+b_3,\cdots ,B_n=b_1+b_2+b_3+\cdots +b_n$

故

$\begin{array}{c}S={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_k{b}_k}=a_1{b}_1+a_2\left(B_2-B_1\right)+a_3\left(B_3-B_2\right)+\cdots +a_n\left(B_n-B_{n-1}\right)\\ =\left(a_1-a_2\right)B_1+\left(a_2-a_3\right)B_2+\left(a_3-a_4\right)B_3+\cdots +\left(a_{n-1}-a_n\right)B_{n-1}+a_n{B}_n\end{array}$

以上称为阿贝尔(Abel)变换，下面我们求 ${\displaystyle {\sum }_{k=1}^n{k}^m}\left(m>0,m\in N\right)$

记

$S_n^{\left(m\right)}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^m},a_k=k,b_k=k^{m-1}$

由阿贝尔(Abel)变换

$S_n^{\left(m\right)}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}^k{b}^k}={\displaystyle \underset{k=1}{\overset{n-1}{\sum }}\left(a_k-a_{k-1}\right)B_k}+a_n{B}_n$

其中

$B_k=1^{m-1}+2^{m-1}+3^{m-1}+\cdots +k^{m-1}=S_k^{m-1},\left(1\le k\le n\right)$

故

$S_n^{\left(m\right)}=n{S}_n^{\left(m-1\right)}-{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}{S}_k^{\left(m-1\right)}}$

通过以上推导我们可以发现，若低幂次和已知，则我们可以通过上式求出高幂次和。

构造数列 $\left\{a_n\right\}$ 为 $1,2,3，\cdots ,n,\cdots$ ，数列为 $\left\{b_n\right\}$ 为 $1,2,3，\cdots ,n,\cdots$ ，

易知数列 $\left\{a_n\cdot b_n\right\}$ 的前n项和

$S_n={\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i{b}_i}=a_1{b}_1+a_2{b}_2+a_3{b}_3+\cdots +a_n{b}_n$ ①

其中令 $b_i=i$ ，则 $B_i={\displaystyle {\sum }_{r=1}^i{b}_r}=\frac{i\left(i+1\right)}{2}\left(i=1,2,3,\cdots ,n\right)$ ， $\Delta a_i=a_{i+1}-a_i$

由Abel变换公式得①式可化为

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i{b}_i}=a_n{B}_n-{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}{B}_i\Delta a_i}$

$\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}i\times i}=n{B}_n-{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}{B}_i\Delta a_i}\\ =n\times \frac{n\left(n+1\right)}{2}-{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}\left(\frac{i^2}{2}+\frac{i}{2}\right)}\\ =\frac{n^2\left(n+1\right)}{2}-\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{i}^2}+\frac{n^2}{2}-\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}i}\end{array}$

化简得

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{i}^2}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

方法三：导数法

导数是高中数学重要的方法之一，是进一步学习高等数学的基础，并且是连接初等数学与高等数学的重要桥梁，使学生由以往静态、有限的常量数学观点过渡到以变化的、动态的、无限的变量数学观点来研究问题 [6] 。利用求导可以将复杂的高幂问题转换成较为简单的低幂问题，因此利用导数解决自然数平方和的问题可以达到事半功倍的效果。

令 ${\displaystyle \underset{k=0}{\overset{n}{\sum }}{x}^k}=\frac{x^{n-1}-1}{x-1}$ ，等式两端同时对x求导后再同乘以x得：

${\displaystyle \underset{k=1}{\overset{n}{\sum }}k{x}^k}=\frac{n{x}^{n+2}-\left(n+1\right)x^{n+1}+x}{{\left(x-1\right)}^2}$

等式两端再次同时对x求导得

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2{x}^{k-1}}=\frac{n^2{x}^{n+2}-\left(2n^2+2n-1\right)x^{n+1}+{\left(n+1\right)}^2{x}^n-x-1}{{\left(x-1\right)}^3}$ ①

对①式取x趋于1的极限，得 $\underset{x\to 1}{\lim }{\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2{x}^{k-1}}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}$ 。

则由洛必达法则可得，

$\begin{array}{c}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=\underset{x\to 1}{\lim }\frac{n^2{x}^{n+2}-\left(2n^2+2n-1\right)x^{n+1}+{\left(n+1\right)}^2{x}^n-x-1}{{\left(x-1\right)}^3}\\ =\underset{x\to 1}{\lim }\frac{n^2\left(n+2\right)x^{n+1}-\left(2n^2+2n-1\right)\left(n+1\right)x^n+{\left(n+1\right)}^{2}n{x}^{n-1}-1}{3{\left(x-1\right)}^2}\\ =\underset{x\to 1}{\lim }\frac{n^2\left(n+2\right)\left(n+1\right)x^n-n\left(2n^2+2n-1\right)\left(n+1\right)x^{n-1}+n\left(n-1\right){\left(n+1\right)}^2{x}^{n-2}}{6\left(x-1\right)}\\ =\underset{x\to 1}{\lim }\frac{n^3\left(n+2\right)\left(n+1\right)x^{n-1}-n\left(n-1\right)\left(2n^2+2n-1\right)\left(n+1\right)x^{n-2}+n\left(n-2\right)\left(n-1\right){\left(n+1\right)}^2{x}^{n-3}}{6}\\ =\frac{n^3\left(n+1\right)\left(n+2\right)-n\left(n^2-1\right)\left(2n^2+2n-1\right)+n\left(n-1\right)\left(n-2\right){\left(n+1\right)}^2}{6}\\ =\frac{n\left(n+1\right)\left(2n+1\right)}{6}\end{array}$

即 $1^2+2^2+3^2+\cdots +n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$ 。

2.3. 几何方法

自然数的平方和有多种证明方法，除了用数学归纳法、待定系数法、积分法等证明方法外，还可以通过将代数问题转化为几何问题进行证明，数形结合思想是一种至关重要的思想，它将抽象的数与直观的形结合起来，从而使复杂的问题以一种更加直观的方式呈现出来，起到优化解题过程的作用。

方法一：面积拼补法

⻓方形是最简洁、最直观的基本图形。构建基于⻓方形的几何模型，能自然流畅地呈现低阶自然数和的推理过程 [3] 。通过单位正方形构造自然数的平方和的几何面积图形，如图中白色部分的阶梯型，将它补成图2的矩形。

Figure 2. The rectangle after the cut

图2. 割补后的矩形图

由图阶梯型的面积为 ${\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}$ ，矩形的面积为 $n{\displaystyle \underset{k=1}{\overset{n}{\sum }}k}$ 。

所补梯形的面积为阴影面积为 ${\displaystyle \underset{k=1}{\overset{n-1}{\sum }}{\displaystyle \underset{r=1}{\overset{k}{\sum }}r}}$ 。

则可以得到所求阶梯型的面积为矩形的面积减去所补梯形的面积即：

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=n{\displaystyle \underset{k=1}{\overset{n}{\sum }}k}-{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}{\displaystyle \underset{r=1}{\overset{k}{\sum }}r}}$ ①

我们已知自然数的前n项和为 $\frac{\left(1+n\right)\cdot n}{2}$ ，可将①式化简为

$\begin{array}{c}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=\frac{1}{2}\left(1+n\right)\cdot n\cdot n-\left[\frac{1}{2}\left(1+1\right)\cdot 1+\frac{1}{2}\left(1+2\right)\cdot 2+\frac{1}{2}\left(1+3\right)\cdot 3+\cdots +\frac{1}{2}\left(1+n-1\right)\cdot \left(n-1\right)\right]\\ =\frac{1}{2}\left(1+n\right)\cdot n\cdot n-\frac{1}{2}\left[\left(1+1^2\right)+\left(2+2^2\right)+\left(3+3^2\right)+\cdots +\left(n-1+{\left(n-1\right)}^2\right)\right]\\ =\frac{1}{2}\left(1+n\right)\cdot n\cdot n-\frac{1}{2}\left[\left(1^2+2^2+3^2+\cdots +{\left(n-1\right)}^2\right)+(1+2+3+\cdots +n-1)\right]\\ =\frac{1}{2}\left(1+n\right)\cdot n\cdot n-\frac{1}{2}\left[\left({\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}-n^2\right)+\frac{1}{2}\left(1+n-1\right)\cdot \left(n-1\right)\right]\end{array}$

移项化简可得

$\frac{3}{2}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=\frac{1}{2}\left(1+n\right)\cdot n\cdot n+\frac{1}{2}{n}^2-\frac{1}{4}n\cdot \left(n-1\right)$

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=\frac{2}{3}\left[\frac{1}{2}\left(1+n\right)\cdot n\cdot n+\frac{1}{2}{n}^2-\frac{1}{4}n\cdot \left(n-1\right)\right]=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

由此推出：

$1^2+2^2+3^2+\cdots +n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

方法二：数阵法

我们学过幂的定义，即 $n^m$ 指m个n相乘。这启发我们将求解自然数的平方和的问题转化为求一列数 $\left\{1,2,2,3,3,3,\cdots ,n,n,n,\cdots ,n\right\}$ 和的问题。

我们可以借助构造如图3的三角形数阵来求解上述问题，其中 $k^2$ 表示k个k之和。将求和数摆到三角形各交点上，摆在第k行的k个位置上，如图：

Figure 3. Triangular array

图3. 三角形数阵

旋转图3三角形数阵得到另两个三角形数阵，如下图4，每一线段上的数字顺序成等差数列，再重叠三个数阵。

Figure 4. The rotated triangular array

图4. 旋转后的三角形数阵

则每一点上的数字和为 $2n+1$ ，则：

$3{\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=\left(2n+1\right){\displaystyle \underset{k=1}{\overset{n}{\sum }}k}=\frac{n\left(n+1\right)\left(2n+1\right)}{2}$

即：

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

该方法不仅可以使学生进一步理解乘方的运算，同时提高了学生数形结合的能力。

方法三：堆垛法

堆垛法也是一种比较直观的几何求和法。堆垛求和法是北宋科学家沈括在观察制酒的过程中发现，酒商为了方便储存，将酒缸一层层的堆起来，形成了堆垛。怎样用简便的方法计算堆垛中酒缸的总数，在古代就称为堆垛术 [7] 。通过对堆垛术本质的分析，实际上它是通过几何代数的变换来研究数列求和问题的，对级数理论的发展产生了深远的影响 [8] 。下面利用堆垛法来解决自然数的平方和的问题。

首先假设单位正方体的体积为1，那么从立体来看，自然数的平方和就是下面所有方块的体积和：(图5)

Figure 5. Geometric representation of the square of a natural number

图5. 自然数的平方的几何表示

将n²看作n²个单位正方体。从上到下用单位正方体作堆垒，从上到下第n层放n²个，将它们堆起来如图6。

最下层为第n层，第n层所堆补的体积为：由长为n，宽为1，高为 $n-1$ 的一个长方体与另一个长为 $n-1$ ，宽为1，高为 $n-1$ 的长方体所组成的几何体的体积。例如第在层的前方添6块单位正方体，右方添4块单位正方体。最后将它补成边长为n的正方体，则共需个n³正方体，即总体积为n³的正方体。

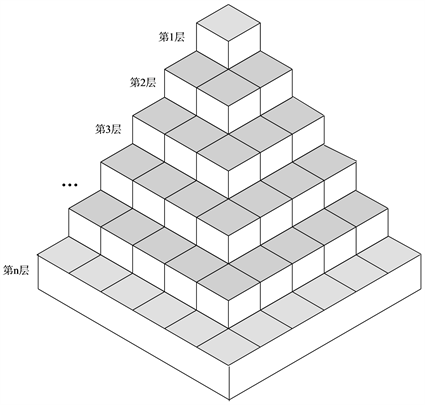
Figure 6. Geometric representation of the sum of squares of natural numbers

图6. 自然数的平方和的几何表示

其中设所求体积为V，每层所补几何体的体积为 ${\bar{V}}_n$ 。

每层所补几何体的体积分别为：

${\bar{V}}_n=n\left(n-1\right)+n\left(n-1\right)\left(n-1\right)=2n^2-3n+1$

则所补几何体的总体积为：

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{\bar{V}}_k}={\displaystyle \underset{k=1}{\overset{n}{\sum }}\left(2k^2-3k+1\right)}=2{\displaystyle \underset{k=1}{\overset{n}{\sum }}{k}^2}-3{\displaystyle \underset{k=1}{\overset{n}{\sum }}k}+n=2V-3\cdot \frac{n\left(n+1\right)}{2}+n$

并且整个正方体总体积为所求体积加上所补几何体的总体积，得：

$n^3=V+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\bar{V}}_k}=V+2V-3\cdot \frac{n\left(n+1\right)}{2}+n$

移项化简得

$3V=n^3+3\cdot \frac{n\left(n+1\right)}{2}-n$

$V=\frac{2n^3+3n^2+n}{6}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

3. 结语

数学知识从来都不是独立存在的，同时数学题型灵活多样，解题方法也是千变万化，各个方法之间都存在着千丝万缕的联系 [9] 。因此在面对同一道题目的时候就要求学生能够迅速并灵活的迁移知识，其次要结合学生已有的解题经验，从多个方面寻求解题思路，选择恰当的解题方法来优化解题方案，提升学生的解题效率。

本文通过介绍以上的几种方法从不同的视角来解决自然数的平方和这个问题，其目的旨在有效的开拓学生的视野和思维能力，一方面提高学生的计算能力和空间解析能力，发展学生的数形结合思想，另一方面也可以激发学生对数学学习的热情，以及对数学的好奇心，从而提高学生抽象思维能力。