1. 引言
推挤绝缘是PTFE电线电缆生产制造之中非常重要的一项工序。与之对应的绝缘推挤机是完成推挤动作的最主要的机器设备。推挤动作要求达到的工艺效果是在线芯圆周紧密的挤出覆盖一层熔融的PTFE材质外壳,要求其厚度要均匀,不得超出规定的误差,对于厚度的精度有较高的要求,同时不得有外壳断裂导致内芯线裸露。在过去线径生产工艺常常用到的控制方法是PID控制,因为其具有效果较为稳定,方法简单等优点而被大量应用到该工艺之中,但不足之处是其参数的选取比较困难,需要人有十分丰富的经验才能快速得到较为满意的三个参数。在参数整定结束后,参数的值保持恒定不变,比较难达到最好的控制效果。在真实的生产条件下,由于PTFE绝缘电缆生产系统具有时变性、非线性、大滞后性的特点 [1] 。所以其控制效果未达到电缆生产的高精度、抗干扰性能强等要求。故需要寻找新的控制方法来优化上述问题,以满足实际电缆生产的需求。
21世纪以来,智能控制科学发展突飞猛进,涌现出非常多智能控制算法。故许多专家学者将智能控制算法引入线径控制之中,以此来帮助解决线径生产中的问题。针对线径生产系统中的大滞后问题,Hussein H. [2] 将动态矩阵预测的方法引入系统中。针对控制系统PID参数整定问题。Li H. [3] 等人将蚁群优化算法引入系统,并结合卡尔曼滤波算法来增强系统整体的抗干扰能力。但会导致整体的运算量剧增,对传递函数也有影响,同时对设备的要求较高,会使控制结果出现一定的偏差。
上述对于线径推挤系统的改进方法都在一定程度上增强了的调节能力,但仍然存在一些不足,例如控制精度有待提升,调节时间稍长,易陷入局部最优。本文引入改进的鲸鱼算法(Improved Whale Optimization Algorithm, IWOA)和动态矩阵控制(Dynamic Matrix Control, DMC)结合的方法。这种方法的优势在于利用IWOA对PID的三个参数进行自动整定,解决PID调参问题。同时用DMC [4] 建立系统模型的预测控制算法,解决系统本身的大滞后问题,具有一定的预判性,使系统可以对干扰做出及时准确的调整。较好的解决了线径生产过程中的控制精度差、非线性和大滞后等问题,具有一定的实际生产价值。
1.1. 线径生产推挤系统
1.1.1. 线径控制系统结构
在理想条件下,电缆线径的生产制作可理解为将PTFT材质熔融之后包裹在一根铜芯线上。完成这一动作的系统按照从头到尾排序主要由放线设备、牵引设备、加热设备,挤塑设备、冷却设备、测量反馈设备、牵引设备和质量反馈设备组成。其系统的整体结构示意图如图1所示。
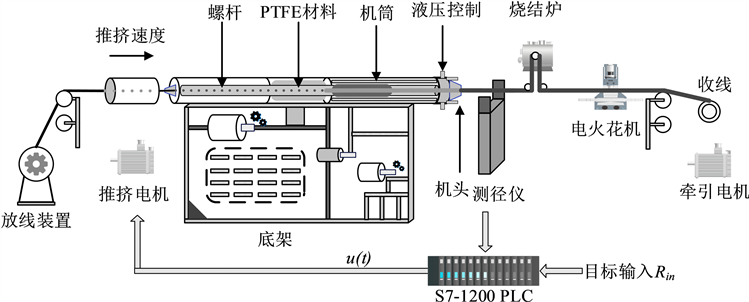
Figure 1. Structure of wire diameter extrusion system
图1. 线径推挤系统结构
金属芯线先经由放线装置和矫正装置,推挤电机作用于螺杆,芯线被螺杆以一定的推挤速度进入推挤机。同时PTFE原料经由供料管道被吸入供料部分,并熔融至可以被推挤的状态。芯线和熔融态的PTFE相遇后经推挤处理后一起被拉出挤塑机头部。然后经过一小段间隔,之后被测径仪检测半径是否合格。之后电缆进过烧结炉和电火花机将质量情况的数据上传,最后电缆由收线装置一起整装待出厂。
1.1.2. 对象模型建立
出于对测径仪的保护要求,机尾和测径仪之间要间隔一定的距离,防止烧坏测径仪。这导致反馈给系统的数据有一定的延迟,带来了一定的滞后性。为方便生产,通常将推挤速度设置为恒定。于是系统的滞后时间τ可用公式求得为
(1)
其中L为机尾到测径仪的长度,Vtraction为系统的推挤速度,即生产速度。其中滞后的环节可以看做是一阶惯性加纯滞后环节,螺杆调速系统为直流闭环调速,模型可等效为二阶惯性环节 [5] 。故其数学模型可以用如下近似表达:
(2)
其中,K为比例系数,T1、T2为惯性时间常数,τ为时滞时间常数 [6] 。根据相关研究成果 [1] [2] [3] ,并且对现场数据收集分析拟合得出较为符合本系统的传递函数为:
(3)
2. 基于IWOA预测PID控制系统设计
2.1. 系统运作原理
在实际线径制造过程中,如果两节胚料的链接处连接不牢固或者两节之间存在空气等干扰都会影响线径的推挤效果。从现场的线径波动数据分析,其差距缓缓减小,然后剧增,振幅较大。此类扰动可等效为一干扰信号。根据分析建立IWOA预测PID线径控制系统,如图2所示。
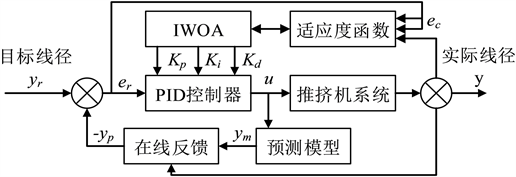
Figure 2. IWOA predictive PID control principle
图2. IWOA预测PID控制原理
系统的控制部分由控制和预测两部分组合共同作用。控制部分的算法是IWOA与PID结合,其原理是将系统控制的目标线径yr与实际线径y的差值er和差值变化率ec作为整个系统的输入量,之后按照适应度作用最后整定出最佳的Kp、Ki和Kd三个参数。预测部分的算法是将系统各参数拟合到一个预测模型之中,在矫正环节之后输出下一时刻的预测线径。然后u是推挤机的控制量(电压),作用于控制对象推挤机。最终使得推挤机的控制效果达到最优,来达到最佳的线径控制的效果。
2.2. 鲸鱼算法及其改进
2.2.1. 鲸鱼算法
鲸鱼优化算法 [7] 的灵感来源与白鲸在大海中的群体猎食行为,目标鱼群代表的是一个解,每个鲸鱼的位置可看做是一个可行解。算法的主体精髓包含三种策略,一种是围猎,群体向目标游动。另一种是围绕猎物呈圆形游动并吐出气泡驱逐猎物。最后一种是基于本身的位置向周围寻找猎物。其动作原理如下:
1) 围猎。在目标鱼群位置为止的情况下,选取鲸群中当前最优的位置为目标位置,剩下的鲸鱼向当前目标位置聚集,更新迭代,直至找出最优解。此一系列动作可用以下数学模型解释:
(4)
模型中的t表示为目前的迭代次数,X(t)和X*(t)分别为第t代和截止t为止的最优解。D为X(t)和X*(t)的空间距离的绝对值。A、C为矩阵系数,两者由随机向量
和线性衰减系数a决定。a的表达式为:
(5)
其中tMax是算法的最大迭代次数。
2) 气泡攻击。鲸鱼呈螺旋状游动并吐出气泡,气泡因为浮力上升并组成空气墙,攻击鱼群。此阶段的动作可用如下数学模型表示:
(6)
其中b为螺旋系数,
为向量。
3) 搜寻目标。鲸鱼在全局范围内寻找目标鱼群,此阶段动作可用如下模型表示:
(7)
模型中Xrand为鲸群中随机一个体。在算法的初期,
时算法执行全局搜索,在
时,算法执行局部搜索,便于快速找到最优解。局部搜索时为实现包围和缩圈的同时运行,采取用相同的p执行包围,用不同的概率1 − p执行螺旋缩圈,可用如下数学模型表示:
(8)
2.2.2. 鲸鱼算法的改进
由于初代鲸鱼算法的一些特性,比如其在前期执行的是全局搜索,且收敛速度较为迅速,后期执行的是局部搜索,这会导致其陷入局部最优解的困境。这也是诸多生物智能算法的通病。另外鲸鱼在搜寻目标阶段的策略较为单一古板,搜寻效果偏向于“随机”,相应的运算量比较繁琐且效率有待提升。
1) 针对鲸鱼算法之所以容易陷入局部最优解的问题,是因为其a的分布呈线性,而原始算法的a是在初始时就呈线性下降,不利于全局搜索,而在后期变化较慢,不利于全局搜索。应尽量多的使a停留在“全局搜索”的区域内,故本文引入新的函数(9)代替原始鲸鱼算法的函数。
(9)
函数(9)在算法执行的前期变化较为缓慢,有利于增强前期俯瞰全局的能力,大大增强其全局搜索性。而在算法执行后期其迅速收敛直至变为0,使其局部搜索能力大幅提升。
2) 针对搜寻效率不高且搜索不均衡的问题,现引入Levy飞行策略 [8] 。Levy被论证为是一种较为高效的仿生随机游走搜索的策略。其执行动作大部分为短步搜索,一小部分为长步跨越穿插在其中。这种长步跨越使得Levy自身具有鲸鱼算法那样精确搜索特性的同时,也具有一定的探索性。有利于算法在迭代时在区域性最优解附近长步探索更优解,避免其陷入局部最优解的误区。为方便在数学模型上复现此策略,本文所使用的Levy飞行数学表示如下 [9] :
(10)
其中s为步长,s的表达式如下:
(11)
其中
,
,β的取值为1.5,σu和σv的取值为如下:
(12)
将新的Levy飞行策略优化至原始鲸鱼算法中,新的搜寻策略为:
(13)
即把式(13)换做式(7)。
2.3. 适应度函数
为了使由算法得出的PID参数的调节效果能有一个衡量的标准,引入适应度函数的概念。适应度可用PID优化的评价指标中的误差绝对值对时间的积分的性能指标,并且加入了输入的平方项来抑制控制能量的增加 [10] 。适应度函数可用下式表示。
(14)
其中,式中:e(t)为输入与输出间的误差值,t,w为权值常数,u(t)为控制量。
考虑到超调量对于评价指标的影响,将超调量也加入评价指标之中,引入惩罚措施来避免产生超调 [11] 。此时的适应度函数式如式(15)所示。
(15)
2.4. DMC预测控制
由于线径制造时芯线从机头被推挤完毕后与测径仪的反馈之间有一定的间隔,从芯线出机头到被测径仪测量反馈至系统的这段时间为τ,τ由推挤速度和机头与测径仪之间的间距l决定,的表达式为
,vw这里的是指线径生产的平均速度。由于系统之后时间的存在导致了系统的控制不是实时进行的,所以需要进行预测控制。
本文采用DMC预测的方法来预测从机头产出的线径数据,在原来时滞的基础上提前τ个时间将预测结果输入系统,大幅提高线径控制系统的性能。其算法的本质是从阶跃响应来调整增量控制,之后以预测模型来对当前时刻的和之前的偏差值为数据进行滚动优化,最后将最合适的结果输入至系统。
2.4.1. 预测模型
模型的建立是以被测对象的输入和输出的数据进行采集为基础的。第一步,对被测对象进行单位响应的采样,其值用
,
表示。第二步依据得到的采样数据建立模型的预测向量,用
来表示,其中N为建模过程中时域的长度。第三步,采取控制变量法,除了其余的条件不变,只在K时间点对对象施加一增量控制
,采集之后由对象反馈的N个输出的数据。
那么在时间点之后对于对象的输出预测值可用如下描述:
(16)
(17)
(18)
其中,是K时间点起系统加入
之后的预测输出。表示系统未加
时的输出值;p表示为系统的优化时域长度;M表示控制时域长度;N表示建模时域长度;(k + 1, k)表示在k时对k + 1的预测。根据对推挤机对象模型的单位阶跃响应进行参考,拟使用采样周期T = 0.5,N = 20,M = 1,P = 15。
2.4.2. 在线校正
实际生产环境下,会存在干扰、建模不准确等因素的存在,得到的预测输出常常与真实的输出有一定的偏差。故必须对预测值进行在线校正以保证预测的拟合性,具体做法是在线校正。即在k的下一时刻把对象的实际输出值与(14)得出的预测输出值ym(k)进行差值处理。
(19)
接下来用由加权系数组成的N维校正向量h以滚动优化的方式实施校正更新:
(20)
其中,
,这里的
是由本系统决定的。γp(k + 1)为校正后的预测输出值,在相位偏移过后其自身以下一时刻的初始预测值的身份进入系统之中。γp(k + 1)可用向量表示为:
(21)
其中s是位移矩阵,可表示为:
(22)
3. 系统仿真与结果分析
3.1. 试验仿真数据
此次仿真的实验选择在MATLAB的Simulink内实施。数据的选取方式是采用到赣州某电缆生产工厂的实际现场采集取得。实验的目的是比较IWOA-DMC-PID控制算法、WOA-DMC控制算法与传统PID算法的控制效果。仿真实验开始时,先对PID三个参数进行初始化,令kp = ki = 0.7,kd = 2.1。传递函数的T1 = 0.84,T2 = 0.46,时间滞后τ = 0.9。设定鲸鱼的最大迭代次数为100,种群大小设置为30。
3.2. 寻优迭代分析
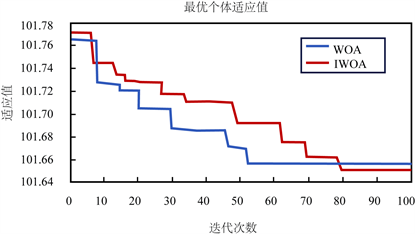
Figure 3. Relationship between fitness value and iteration number
图3. 适应值与迭代次数的关系
由图3可知,WOA的迭代次数为53次左右的时候迭代完成,并且适应值在101.66左右,而IWOA的迭代次数为63次数左右,并且相较于WOA的适应度值小,这说明了WOA算法虽然迭代次数少但是陷入了局部最优情况,没有得出全局最优的最佳一组参数,而IWOA则有效避免了这种局部最优解的情况,准确的找到了全局最优解。
3.3. 脉冲响应分析
为了比较三种控制方法的控制效果,设置线径值为2 mm。当系统未受外界扰动时分别对三种控制方式进行仿真,三种方式的控制效果如图4所示。由图中曲线可以得到,采用传统的PID算法时的系统超调量σ约为27.5%,达到运行平稳所需的调节时间ts约为30秒,调节过程中线径波动较大,响应较为迟钝,调节时间较为漫长。采用WOA-PID的结合算法,系统调节的效果有所提升,系统超调量σ约为15.4%,调节时间ts约为21秒,整体过程的控制线径波动比传统PID调节效果稳定,但依然有很大提升空间。而采用IWOA-DMC-PID复合控制算法时,系统的超调量σ约为0,调节时间ts为10秒,但系统的响应时间稍长。
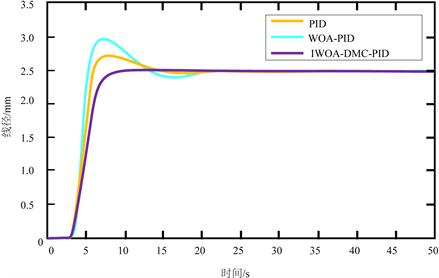
Figure 4. Three types of pulse response curves
图4. 三种方式的脉冲响应曲线
3.4. 抗扰动性能分析
在三种控制方式达到稳定运行状态后,在30秒对系统施加一个单位为1的阶跃扰动,其三种控制方式的仿真曲线如图5所示:
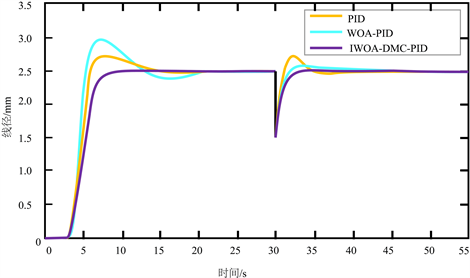
Figure 5. Three ways to add disturbance response curve
图5. 三种方式加扰动响应曲线
由图5中的相应曲线可知,普通PID在扰动出现后可做出最快反应,但是其控制线径的波动也十分剧烈,到达稳定的调节时间为23秒。采用WOA-PID结合算法反应时间较传统PID的稍慢,但是线径的波动情况有所改善,但线径值仍有波动。采用IWOA-DMC-PID复合算法的反应时间与前两者相当,但是在线径波动和调节时间方面都有极大的改善,线径值程平滑改变的趋势,几乎无波动。这说明了三种方式中IWOA-DMC-PID具有良好的抗干扰性能。
3.5. 鲁棒性测试分析
由于在实际的工厂生产条件下,由于电磁干扰等因素的存在,会导致数学模型发生变化,而模型的变化会影响控制效果甚至对系统失去控制。所以要求整个系统具有较强的鲁棒性,即使系统参数或者系统特性因为外因发生变化时,系统也能有维持现状,也能保持较好控制效果的性能。本文将数学模型的增益与时滞各自增大40%后以三种控制方式进行仿真,得到的响应结果如图6所示。
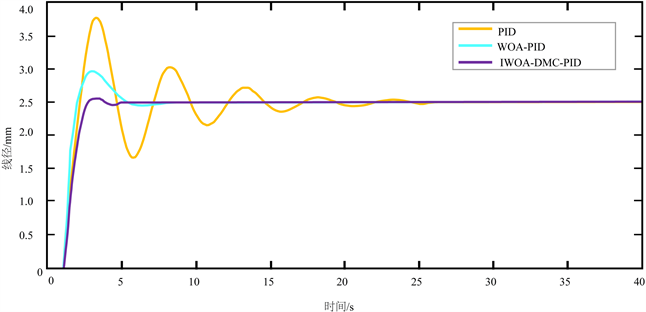
Figure 6. System response diagram after parameter changes
图6. 参数改变后的系统响应图
由图6可知,在数学模型改变后,普通PID的调节效果整体呈现出较大幅度的震荡,且调节时间最长,约为27秒。WOA-PID的调节效果较传统PID有一定的提升,调节时间约为11秒。最后IWOA-DMC-PID的调节效果对比前两者有大幅度提升,系统震荡最小,几乎无震荡,且调节速度很快,只需7秒即可达到稳定。这表明三种方式中IWOA-DMC-PID的鲁棒性最佳。
4. 结论
本文针对传统PID参数调节困难,控制效果不佳,智能算法与PID结合寻优易陷入局部最优的问题,本文引入鲸鱼算法与DMC与PID结合并应用于线径推挤系统。通过对鲸鱼算法进行改进,并且改进之后在Matlab中编程并用SIMULINK对PID,WOA-PID与IWOA-DMC-PID三种控制方式进行仿真,结果表明,采用IWOA-DMC-PID控制效果比其他两种控制方式的效果好。线径挤出系统能够将挤出的线径稳定控制在3.5 mm左右,并且对于外界的干扰有较好的快速响应的能力,具有较强的鲁棒性,可以满足实际线径挤出的生产要求。