基于特征提取和LSTM的PM _2.5浓度预测模型

PM _2.5 Concentration Prediction Model Based on Feature Extraction and LSTM

摘要: PM_2.5是空气污染中对人体危害最大的一类污染物之一，对PM_2.5的准确预测可以为人们社会活动的决策制定提供可靠依据。使用自编码器(Auto-encoder)能够达到较高的预测精度，但是需要训练的参数量大，所需的计算资源也会增加，于是本文提出了一种待训练参数比Auto-encoder减少了24%的PM_2.5预测模型FE-LSTM (Feature Extraction-LSTM)。FE-LSTM模型基于SE注意力机制、卷积神经网络(CNN)和长短期记忆网络(LSTM)等模块，先使用CNN提取出输入张量的初始特征，再通过SE注意力对特征张量按通道加权，通过全连接和重构后使用LSTM得出污染浓度的预测值。在北京PM_2.5数据集上，对FE-LSTM模型及对比模型进行了训练和测试，结果表明，本文所提出的FE-LSTM模型的预测精度优于其他对比模型。

Abstract: PM_2.5 is one of the most harmful pollutants in air pollution, and accurate prediction of PM_2.5 can pro-vide a reliable basis for decision making in people’s social activities. This paper proposes a PM_2.5 prediction model, FE-LSTM (Feature Extraction-LSTM), with 24% fewer parameters to be trained than Auto-encoder, which can achieve high prediction accuracy but requires a large number of training parameters and increased computational resources. The FE-LSTM model is based on the SE attention mechanism, convolutional neural network and long short-term memory network mod-ules. The initial features of the input tensor are first extracted using CNN, then the feature tensor is weighted by channel through SE attention, and the predicted pollution concentration is derived us-ing LSTM after full concatenation and reconstruction. The FE-LSTM model and the comparison mod-els were trained and tested on the Beijing PM_2.5 dataset, and the results showed that the prediction accuracy of the FE-LSTM model proposed in this paper was better than that of the other comparison models.

1. 引言

长期处于高污染空气中的人容易患有哮喘、肺病甚至癌症等疾病，其中PM_2.5直径小，被人体吸入后可深入到肺泡，直接影响心肺功能。近年，我国已高度重视大气污染相关问题，针对不同地区制定了不同的减排目标，空气污染预测对于排查污染源、治理空气质量有着重大意义。可靠的大气污染预测模型可以提前给大众提供大气污染预警信息，警醒有关环保部门采取反制措施。

因此，很多专家和学者对大气污染预测开展了研究。例如，孙宁 [1] 等人使用PSO-SVR方法预测北京的PM_2.5浓度，利用PSO算法优化SVR模型中的相关参数，达到了比单个SVR模型更好的预测精度。Salina [2] 等人结合了物联网技术和双向循环神经网络(RNN)模型实现了美国PM_2.5浓度的监测和预测系统。Dairi等 [3] 开发了一个集成多方向注意力的变分自编码器预测模型(IMDA-VAE)，并在美国四个州的空气数据上进行了实验验证。张波 [4] 等人提出了一个CAE-Learning模型，先使用CNN模型学习到污染物和天气因素之间的关联特征，然后利用基于LSTM的自编码网络实现多站点的特征分析。宋飞扬 [5] 等人提出了一个基于时空特征的KNN-LSTM模型，考虑了多个监测站之间的区域关联，用于预测哈尔滨市的PM_2.5浓度，达到了比BP和LSTM模型更好的预测效果。Zhang [6] 等人提出了一种基于自编码器和双向LSTM的深度学习模型来预测PM_2.5浓度，实验结果证明该自编码器的预测精度优于空气污染预测数值模型和几种机器学习模型。Qiao [7] 等人提出了一个基于小波变换、自动编码器和长短期记忆网络(LSTM)的组合模型来预测多个城市的PM₁₀浓度。Jin等 [8] 提出了一个基于经验模态分解(EMD)，卷积神经网络(CNN)和门控循环单元结构(GRU)的组合模型来预测北京市的PM_2.5浓度。上述学者使用多种机器学习或深度学习方法来预测大气污染浓度，并取得了很好的预测精度，但是没有考虑到模型中需要训练的参数量，可能导致模型过大而无法部署在资源受限的设备上，应用前景不够广泛。

本文提出了一种基于特征提取和LSTM的PM_2.5浓度预测模型FE-LSTM，在提升预测精度的同时，尽量减少模型中需要训练的参数量，试图花费较少的计算资源来获得更高的预测精度。该模型利用特征提取模块提取出输入张量的特征值，然后输入到LSTM中进行预测。其中，特征提取模块使用的是CNN和SE-Attention相结合的结构，通过CNN将时间序列转化为三维特征张量，然后使用SE-Attention加大重要特征的权重，这将有助于LSTM结构保留重要信息。

2. FE-LSTM模型

本文提出的FE-LSTM模型结构如图1所示，在LSTM之前加入特征提取模块，在特征提取模块中使用CNN初步提取出输入序列的特征张量，由于多核卷积生成的特征张量的不同通道会学习到不同的特征，某些通道的特征对于后续预测不太重要，为了使LSTM模型能够更好地学习到特征值，使用SE-Attention分别计算初始特征张量中各个通道的权重，并将归一化后的权重和原始特征张量相乘，得到加权后的特征张量。再经过全连接和重新排列，得到的新特征矩阵输入到LSTM结构中进行预测，这有助于更重要的特征存入LSTM单元的长期细胞状态中，从而提升模型精度。

图1. FE-LSTM模型结构图

2.1. 特征提取

FE-LSTM模型中使用特征提取模块进行序列变换，其具体步骤如图2所示，先使用卷积神经网络对输入序列进行多核卷积和池化后得到多个通道的初始特征张量，然后使用SE-Attention在初始特征张量的通道尺度上进行加权处理，得到权重特征张量，再通过全连接将通道数减少为1，并重构成二维矩阵。

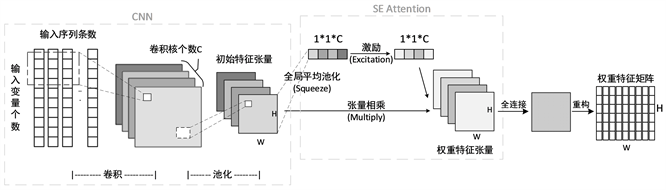
Figure 2. Structure of the feature extraction module

图2. 特征提取模块结构示意图

1) 选用CNN提取输入序列的初始特征张量。卷积神经网络(CNN)是多层感知机的变种 [9] ，具有局部感知和权重共享的特性，这有效减少了计算量，减轻了训练时对设备算力的严苛要求。如图2所示，本文使用的是2D-CNN，将输入序列看作通道数为1的二维矩阵，卷积核的数量C即为卷积的次数，每次卷积都能得到一个特征矩阵，最终得到通道数为C的特征张量。卷积部分的计算公式如公式(1)所示。

$X^{\prime }={\delta }_{relu}\left(\left(K_C\otimes X\right)+b_C\right)$ (1)

其中，X为输入矩阵， $X^{\prime }$ 为提取出的特征张量， $K_C$ 表示卷积核的权重系数， $b_C$ 表示偏置向量。 $\otimes$ 表示卷积操作， ${\delta }_{relu}\left(\mathrm{..}\right)$ 表示激活层，具体如公式(2)所示。

${\delta }_{relu}\left(z\right)=\{\begin{array}{c}0,z<0\\ z,z\ge 0\end{array}$ (2)

卷积神经网络中池化操作可以在不影响特征的本质的前提下减小特征矩阵的维度，减少后续的计算量。在FE-LSTM模型中使用了2*2最大池化，将卷积结果中每个2*2子矩阵中的最大值作为新矩阵的值，对C个特征矩阵都进行上述池化降维操作后，得到维度为W*H*C的初始特征张量 $X_p$ ，其中W、H分别表示初始特征张量的宽和高。

2) 选用SE-Attention对初始特征张量 $X_p$ 的各个通道加权。SE模块是由Hu [10] 等人提出，通过学习通道间的依赖关系来增强特征。为了计算各个通道的权重，先对每个通道的特征矩阵做全局平均池化(Squeeze)计算，得到每个通道的平均值即维度为1*1*C的张量。其计算过程如公式(3)所示。

$X_{sq}=\frac{1}{W\text{*}H}\underset{i=1}{\overset{H}{{\displaystyle \sum }}}\underset{j=1}{\overset{W}{{\displaystyle \sum }}}{X}_p\left(i,j\right)$ (3)

在激励(Excitation)的过程中，使用了两次全连接层得到通道的权值，第一次全连接压缩通道值至C/4，第二次全连接恢复通道数至原来的值C，先压缩再恢复能够减少需要训练的参数量至原来的1/4。使用sigmoid激励函数将权值映射到0~1之间，得到归一化后的通道权值 ${\tilde{X}}_c$ 。其计算过程如公式(4)所示。

$X_{sq}=\frac{1}{W\text{*}H}\underset{i=1}{\overset{H}{{\displaystyle \sum }}}\underset{j=1}{\overset{W}{{\displaystyle \sum }}}{X}_p\left(i,j\right)$ (4)

其中，W_s、b_s和W_r、b_r分别表示两次全连接层的权重系数和偏置向量， ${\sigma }_{Sig}$ 计算过程如公式(5)所示。

${\sigma }_{Sig}\left(z\right)=\frac{1}{1+{\text{e}}^{-z}}$ (5)

然后将待加权的初始特征张量 $X_p$ 和权值 ${\tilde{X}}_c$ 相乘，将通道维度上的权重加入到特征张量中，得到权重特征张量 $X_{FE}$ 。

3) $X_{FE}$ 为三维张量，不能直接输入到LSTM网络中，需要将其重构成二维矩阵。在此之前，使用全连接层将通道数为C的特征张量 $X_{FE}$ 映射成通道数为1的张量，这能缩减重构后的二维矩阵的大小，大大减少后续LSTM结构中需要训练的参数数量。最后将此维度为W*H*1的张量重构成维度为W*H的二维矩阵，输入到LSTM结构中。

2.2. LSTM结构

LSTM最早由Hochreiter和Schmidhuber [11] 提出，其单元结构 [12] 如图3所示。相比RNN，LSTM新增了遗忘门 ${\sigma }_f$ 、输入门 ${\sigma }_i$ 、输出门 ${\sigma }_o$ 三个结构，能够解决RNN容易出现梯度消失或梯度爆炸的问题，将过去的信息存储在内部的细胞状态中，随着新的输入递归更新。

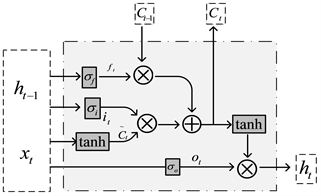
Figure 3. Structure of the LSTM unit

图3. LSTM单元结构示意图

图中， $x_t$ 、 $C_t$ 和 $h_t$ 分别表示当前时刻的输入、细胞状态和输出， $C_{t-1}$ 和 $h_{t-1}$ 分别表示上一时刻的细胞状态和输出， $\sigma$ 表示神经网络层，选用Sigmoid作为激励函数，其输出范围为0~1，代表门限的开关。遗忘门、输入门和输出门的计算分别如公式(6)~(8)所示。

$f_t={\sigma }_f\left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$ (6)

$i_t={\sigma }_i\left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)$ (7)

$o_t={\sigma }_o\left(W_o\cdot \left[h_{t-1},x_t\right]+b_o\right)$ (8)

其中， $W_f$ 、 $W_i$ 和 $W_o$ 分别表示遗忘门、输入门和输出门需要训练的权重矩阵， $b_f$ 、 $b_i$ 和 $b_o$ 分别表示遗忘门、输入门和输出门需要训练的偏置向量。临时细胞状态 ${\tilde{C}}_t$ 、当前细胞状态 $C_t$ 和输出 $h_t$ 的计算分别如公式(9)~(11)所示。

${\tilde{C}}_t=\tanh \left(W_c\cdot \left[h_{t-1},x_t\right]+b_c\right)$ (9)

$C_t=f_t\times C_{t-1}+i_t\times {C^{\prime }}_t$ (10)

$h_t=o_t+\tanh \left(C_t\right)$ (11)

2.3. 超参数选择

超参数需要在训练之前设置，本文使用网格搜索来确定最优的超参数组合，在FE-LSTM模型中，需要人为设置的超参数有：训练时的学习率lr、批处理大小batch_size、CNN卷积核个数filter、卷积核大小kernel、卷积核的滑动步长strider以及LSTM的隐藏单元个数hidden_size。经过实验比较，超参数取值如表1所示。

Table 1. Hyperparameter values chosen for the FE-LSTM model

表1. FE-LSTM模型选用的超参数值

3. 实验结果与对比分析

3.1. 数据集介绍

为了验证提出模型的有效性，本文使用北京PM_2.5数据集进行了测试。该数据集由Liang [13] 等人收集并在UCI [14] 数据集平台发布，包含2010年1月1日至2014年12月31日美国驻华大使馆附近的PM_2.5数据和北京首都国际机场的气象数据，包括露点、温度、气压、风速、降雪量和降雨量等。其数据间隔为一个小时，共43,800条数据。在实验中将此数据集划分为数据集、验证集和测试集，数据比例分别为0.7、0.15和0.15。

3.2. 模型评价指标

采用均方误差(MSE)、平均误差(MAE)、R²系数用于评估模型性能。其中MSE和MAE越大说明模型效果越差，R²系数取值范围为0~1之间，越接近1模型效果越好。它们的计算分别如公式(12)~(14)所示。

$MSE=\frac{1}{N}\underset{i=1}{\overset{N}{{\displaystyle \sum }}}{\left({\tilde{Y}}^i-Y^i\right)}^2$ (12)

$MAE=\frac{1}{N}\underset{i=1}{\overset{N}{{\displaystyle \sum }}}\left|{\tilde{Y}}^i-Y^i\right|$ (13)

$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^N{\left({\tilde{Y}}^i-Y^i\right)}^2}{{{\displaystyle \sum }}_{i=1}^N{\left(\bar{Y}-Y^i\right)}^2}$ (14)

其中， ${\tilde{Y}}^i$ 是i时刻PM_2.5的预测值， $Y^i$ 是i时刻PM_2.5的真实值，N为测试集样本数量， $\bar{Y}$ 表示PM_2.5真实浓度的平均值。

3.3. 对比模型介绍

为了评估本模型在空气污染预测中的性能，选取LSTM，bi-LSTM，Auto-encoder和Cnn-AE等模型进行了对比实验。

训练这四种基准模型时，由于每个模型的收敛速度不一样，在实验中使用早停法(Early Stopping)而非固定值。早停法能让模型得到充分训练的同时避免过拟合，当25个epoch后模型在验证集上的误差仍没有下降的时候停止训练，训练上限为300个epoch。采用的是Adam优化器来优化深度学习模型，损失函数被设置为均方误差(MSE)。

其余超参数使用网格搜索来选取，其中，LSTM神经元数量hidden_size从16，64，128中选取，学习率lr从0.01、0.001和0.0001中选取，batch_size从64，128，256中选取，各个模型最终选用的超参数如下：

1) LSTM模型选用简单的LSTM单元和全连接层的结构，LSTM神经元数量取128，batch size为128，学习率选取0.001。

2) Bi-LSTM模型选用Bi-LSTM和全连接层的结构，LSTM神经元数量取128，batch size为128，学习率选取0.001。

3) Cnn-LSTM模型，输入数据通过filters为64，卷积核大小为4，步长为1的2D卷积层，提取出的特征值输入到上述LSTM模型。

4) Auto-encoder模型中编码器和解码器中都使用相同的LSTM结构，分别从一层或两层，单向或双向的LSTM单元中选取，经过测试单层双向神经元数量128为最优结构，并选取batch size为128，学习率选取0.001。

5) Cnn-AE模型，输入数据通过filters为64，卷积核大小为4，步长为1的2D卷积层，提取出的特征值输入到上述Auto-encoder模型。

3.4. 实验结果

在北京PM_2.5数据集上，使用本文提出的FE-LSTM模型和上述5个对比模型进行预测对比测试，即输入前十个小时的气象信息和PM_2.5浓度来预测之后一个小时的PM_2.5浓度，实验结果如表2所示。从表2可以看出，本文提出的FE-LSTM模型在北京PM_2.5数据集上的MSE和MAE误差值均低于其他对比模型，R²相关系数均高于其他对比模型，FE-LSTM模型相较于LSTM、Bi-LSTM、Cnn-LSTM、Auto-encoder和Cnn-AE在测试集上的MAE误差分别降低了24.71%、22.06%、5.37%、20.41%和2.52%，MSE误差分别降低了21.60%、18.32%、19.52%、17.76%和14.38%，这证明了FE-LSTM模型的预测值更贴近真实值，预测精度更高。加入特征提取后的预测精度明显优于单一的LSTM模型，也证明了本文设计的特征提取模块的有效性。

Table 2. Comparison of prediction results from multiple models on the Beijing PM2.5 dataset

表2. 在北京PM_2.5数据集上各模型预测结果比较

各个模型中需要训练的参数量如表3所示，包括权重和偏置向量等，通常状况下，参数量越大的深度学习模型需要更多的计算资源和时间来更新和优化，会影响到模型的训练时间。在资源受限的设备上部署模型时也需要考虑到模型的参数量，参数量较小的模型更容易在嵌入式设备上运行。

Table 3. The number of parameters to be trained for each model

表3. 各模型需训练的参数量

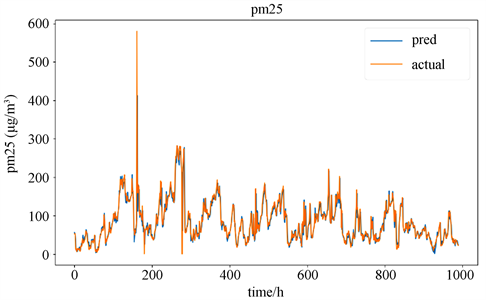
Figure 4. Visualisation of predicted and true values of the FE-LSTM model

图4. FE-LSTM模型预测值和真实值可视化

从表3可以看出FE-LSTM模型需要训练的参数只比LSTM增加13.58%，比Auto-encoder减少了23.48%，这说明FE-LSTM模型能够花费较少的计算资源就可以实现更为准确的预测结果。

FE-LSTM模型在测试集前1000条数据上的PM_2.5浓度预测值和真实值的可视化曲线如图4所示，其中蓝色曲线为预测数据，橙色曲线为真实数据。从图4中可以看出，本文提出的模型预测效果较好，能够预测出PM_2.5浓度的变化趋势，但是在峰值和谷值等数据突变处表现一般。

4. 结论与展望

本文提出了一个基于特征提取和LSTM的PM_2.5浓度预测模型，先使用卷积神经网络提取出输入序列的初始特征张量，再使用SE-Attention机制得到带有权重信息的加权特征张量，然后输入到LSTM结构中得到预测结果。在北京PM_2.5数据集的测试结果表明，本文提出的模型能很好地预测出PM_2.5浓度值的变化趋势，与其余五个基准模型相比，FE-LSTM预测出的数据和真实值更为贴近，相关系数均高于其余几个模型，均方误差和平均误差均小于其余模型，预测精度更高。FE-LSTM模型能够在确保精度的前提下降低需训练的参数量，表明该模型耗费的计算资源更少，便于部署在资源受限的设备上，能够在轻量级的嵌入式设备上运行，具有一定的应用价值。

本文提出的FE-LSTM模型仍有提升空间，由图4的预测曲线可以看出本模型在突变处的预测效果不太理想，之后可以继续尝试将更前沿的先进算法加入模型中，例如引入对突变数据敏感度更高的相关算法，来获得更高的预测精度。

基金项目

浙江省公益技术研究项目(2015C31024)。

参考文献

NOTES

^*通讯作者。