1. 引言
随着CMOS工艺越来越成熟,硅光子学已经成为最具潜力的光学研究平台之一。微环谐振器作为硅基集成光电子器件的关键部分,具有集成度高、结构紧凑、损耗低、扰动小、响应速度快等优点,可以构建成各种光波导器件,因此受到了国内外研究人员的广泛关注,促进了光电子行业的迅速发展 [1] [2] 。各研究课题组在设计高品质因子、低损耗的微环谐振腔方面做出了很大的贡献。
近年来,科研人员基于SOI技术研制出了很多光学传感元器件,例如马赫–曾德尔干涉仪传感器、亚波长光栅传感器、表面等离子体光纤位移传感器、微环谐振器以及微盘谐振器等。由于微纳布拉格光栅其特殊的物理结构,可以使波导传输的光与外界环境产生强烈的作用,使微环元件具有高灵敏度的特性。传感器的原理是改变外部环境折射率后,光波导器件的有效折射率也会跟着改变,引起谐振波长的飘动。周围环境的折射率是传感器计算中一个非常关键的参数,折射率传感器的作用是通过折射率来检测周围环境的变化,可以反映出被检测的物质的折射率改变的精度和范围,因此高品质因子高灵敏度的微环谐振器常用在各个传感领域当中 [3] [4] [5] 。在各个硅基波导元器件中,微环谐振器的结构体积小易集成,非常适合用来做高灵敏度折射率传感器。
以提高微环谐振器的品质因子和灵敏度为出发点,借鉴亚波长光栅微环谐振腔的结构,本文提出了一种基于圆孔光栅辅助的微环谐振器,我们把光栅加在微环和直波导上,把微环和直波导变成两个腔之间的耦合,可以选择性的让一到两种模式通过,其他模式则无法通过,这样的话能量很集中,信号很明显,灵敏度也就会很高。
2. 基本原理
2.1. 理论分析
光子晶体简介:光子晶体是指由两种或者两种或以上不同折射率的介质进行周期性排列构成的人造晶体,它可以分为一维,二维及三维光子晶体。光子晶体具有周期性的电介质结构。晶体内部的原子是周期性有序排列的,由于这种周期性介质的存在,使得电子的运动受到周期性的布拉格散射,形成能带结构,能带与能带之间存在间隙。当电场的能量落在带隙中,就无法继续传播。在某种特定的晶格常数和介电常数比的条件下,光子晶体的能带隙可以使某些频率的电磁波完全不能透过,我们将此频率区域称光子禁带。相反,可以透过的电磁波的频率区域我们称之为光子导带。
微环谐振机制为当光在微环中传输时,绕微环传输一周时所产生的光程差为波长的整数倍的光能产生谐振而加强,即满足:
式中:R为微环的谐振半径,λ为真空波长,m为谐振级数(从1开始的整数),nc表示模的有效折射率。
自由光谱范围:两个相邻谐振模式之间的波长或者频率之间的间隔之差称为自由光谱范围(FSR)。表达式如下:
品质因子,又称Q值,表征微环谐振腔的储能能力,定义为谐振器内部储存的能量与光在谐振腔内传输一周损耗的能量的比值,是决定环腔性能的关键参数,对设计微环谐振器有重要的意义 [6] [7] 。公式如下:
其中,
代表线宽,也就是半高全宽,即取在谐振峰最高处的一半位置的波长宽度大小。
传统的直通微环谐振器的结构模型如图1所示,直通光波导谐振腔是最基本的光学谐振腔结构,由一个环形谐振腔和一根直波导构成。光源的光从输入端进入光波导谐振腔内,经过耦合区域后,一部分光耦合进入谐振腔内绕环传输,每次经过耦合区域时都会有一部分光耦合出直波导进入到输出端。假设输入光场为Ein,输出光场为Eout,谐振腔内耦合区域前后的光场分别为E1和E2,耦合区域的耦合系数和透射系数分别为k和t,k与t满足k2 + t2 = l。

Figure 1. Analysis model of straight-through micro ring resonator
图1. 直通型微环谐振器分析模型
2.2. 结构设计
如图2所示,基于片上硅基光波导器件结构,本文提出的结构是有一根直波导和回音壁微环所组成,并在微环和直波导上加入了呈周期性排列的空气孔作为光栅。在直波导左侧端口导入光,加入了空气孔的微环的波导结构可以将大部分光限制在小孔中,孔状光栅会反射一小部分的光,同时让剩余的光通过到右侧端口。通过分析硅材料的弯曲损耗,采用环形波导的半径r为7 μm,波导宽度w0为1 μm,圆孔光栅半径r0为150 nm,直波导的长度为23 μm,硅的折射率为3.4757 [8] 。选取TE偏振模式。根据光栅在波导的不同位置,可以实现微环与法布里–珀罗腔组成不同的结构,当光在光栅腔内传播时,微环的腔和直波导的腔之间发生耦合,从而形成Fano共振现象,Fano谱线是一种非对称线性的共振现象 [9] ,由于模式的劈裂可以得出更高的Q值,即谐振处的波长与线宽的比值,也可以检测出周围环境改变时产生的较小波长的偏移。
3. 仿真结果
本文所提出结构采用有限元法对传输谱线和模场分布进行建模仿真,因为光子晶体腔和微环之间会发生很强的谐振效果,所以网格划分会采用尺寸较小的网格来进行网格区域的计算,以达到高仿真精度的结果。布拉格光栅的散射损耗会导致部分的能量散射到波导中或波导外部,微环谐振腔的损耗主要包括散射损耗、耦合损耗和弯曲损耗,但由于硅基波导的高折射率对比度,即当微环的半径大于3 μm时,弯曲损耗可以忽略不计 [10] [11] ,并且本结构的微环半径采用7 μm。此外,通过对比条形光栅以及圆孔光栅的本征Q值,得出条形光栅的本征Q值为3.6 × 105,而本文提出的圆孔光栅的本征Q值在4 × 107,和条形光栅相比具有更低的散射损耗。
模场分布如图3所示,从图中可以清晰地看出光场被限制性地分布在空气孔内,耦合效果非常明显,可以达到非常高的灵敏度以及Q值。
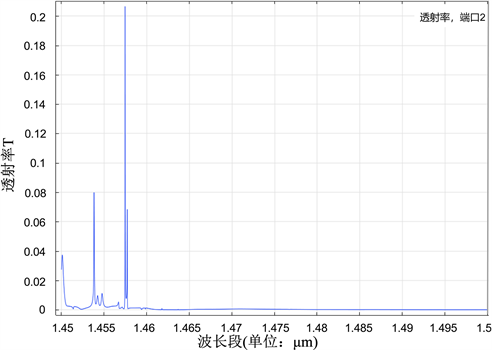
Figure 4. Transmission lines between 1450 nm and 1550 nm
图4. 1450 nm~1550 nm的传输谱线
传统的通光型直波导与环腔构成的微环谐振器的传输谱线是dip线形,然而从图4中光谱的仿真结果可以看出,本文中的微环结构由于在直波导内加了光子晶体,形成了滤波型直波导,可以减少由于模式太多而导致的能量分散,因此传输谱线为peak线形。由图可知,光在光子晶体禁带区域1460 nm~1550 nm内,光无法在光子晶体波导内进行传输;光在导带区域时,满足谐振条件的光进入微环发生谐振,不满足谐振条件的光将透射过直波导。谐振波长处透射率最高的传输谱线,产生了很好的法诺现象,根据品质因子Q的计算公式,计算出本结构的Q值达到了5.83 × 104。
4. 折射率传感特性
灵敏度是衡量传感器传感能力高低的重要参数之一,定义为传感器信号变化量与待测物质折射率变化量的比值。将待检测液体加入该结构的光子晶体内,待检测液体内杂质的浓度发生改变导致待测液体折射率发生变化,波导内的有效折射率也因此改变,此时谐振波长发生偏移。图5显示了光子晶体内不同折射率下的光场透射频谱。设置了从1~1.3范围内4个不同的折射率,当折射率增加时,谐振波长产生红移。我们一般用微环谐振腔的Q值代表光谱中谐振处peak的尖锐程度,因此当采用光谱漂移法检测时,传感的灵敏度与微环的Q值有着直接的关系。在某一个波长处,根据Q值等于波长和半高全宽的比值,谐振模式所对应的线宽越窄,在这个波长段的Q值就越高,进而用来做传感器时的灵敏度和精度也会越高。相反,线宽越宽时,Q值越小,传感的灵敏度就越差。从图中可以明显地看出光谱呈现的透射率下降的趋势是非线性的,但变化的趋势非常的直观,本文仅展现出设计的微环传感灵敏度变化的趋势即可,没有对折射率变化区间进行特别精细化的计算。这里需要注意若想实现高Q值的微环,减小损耗是关键因素一。当增大环半径时,可以减小弯曲损耗和散射损耗,但根据公式:
(其中ng为群折射率),当环半径增大时,FSR会随之减小,会影响器件的通信带宽指标。因此,微环谐振器的高Q值、高灵敏度和高探测范围不能兼得。
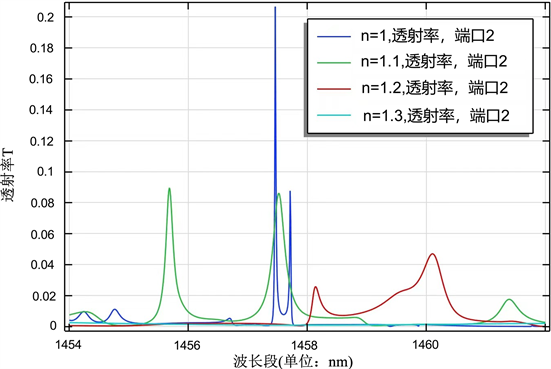
Figure 5. Comparison of spectral lines under different refractive indices
图5. 孔内不同折射率下的光场传输谱线对比
5. 总结
本文设计了一种基于布拉格光栅的椭圆空气孔状微环谐振器,在传统的通光形直波导微环谐振器的基础上进行了改进,通过在直波导内加入光子晶体,形成了滤波型直波导,并且与光子晶体环腔形成了两个腔之间的强耦合特性,效果显著。在该结构中由于同一种状态的光模式在不同的光路中产生模式劈裂而形成Fano共振现象,达到更高的Q值与灵敏度。采用有限元法对设计的结构进行仿真,从光场可以看出在强耦合的性能下光被限制在空气孔内进而达到更高的灵敏度为进行传感研究作铺垫。在波长1457 nm处,灵敏度为475 nm/RIU,品质因数为58,300。综上所述,所设计的光波导器件易于集成,在光学传感领域中具有不错的潜力。
NOTES
*通讯作者。