贝叶斯时空模型在新冠风险评估中的应用

Application of Bayesian Spatio-TemporalModel in the Risk Assessment of COVID-19

摘要: 基于2020~2021年河南省18个地级市新冠肺炎确诊病例数据，采用BYM (Besag-York-Mollie)、FBM (Familiar Bayesian Spatio-temporal)模型来分析新冠肺炎发病风险的时空分布特征，并探讨社会经济、 生态环境等因素对疾病风险的影响效应，同时就应用结果对比两种模型的优劣。方法：收集2020~2021 年河南新冠肺炎确诊数据，采用相关性分析排除部分相关性不大的影响因子，并运用因子分析降维诸指 标，而后分别代入两模型进行分析、讨论。结果：1) 2020~2021年河南全省的疫情风险程度是呈现下 降趋势的，高风险地区主要集中于豫北地区。2) 因子分析共构建基本经济因子、社会因子、温度因子、 降水因子以及空气质量因子五个综合指标。3) 通过模型运行后的结果和DIC值可以得出FBM模型总体要 优于BYM模型。

Abstract: Based on the data of confirmed cases of COVID-19 in 18 prefecture-level cities in Henan Province from 2020~2021, BYM (Besag-York-Mollie) and FBM (Familiar Bayesian Spatio-temporal) models were used to analyze the spatial and temporal distribution characteristics of the risk of COVID-19,and explore the influence of socioeconomic and ecological factors. The results of this study were also used to compare the advantages and disadvantages of the two models. Methods: The data of confirmed cases of COVID-19 in Henan from 2020 to 2021 were collected, correlation analysis was used to exclude some influencing factors with little correlation, and factor analysis was applied to downscale the indicators, which were then analyzed and discussed by substituting into the two models. Results: 1) The risk level of the epidemic in Henan province from 2020 to 2021 showed a decreasing trend, and the high-risk areas were mainly concentrated in the northern part of Henan. 2) The factor analysis constructed five comprehensive indicators: basic economic factor, social factor, temperature factor, precipitation factor and air quality factor. 3) The results and DIC values after the model run can be concluded that the FBM model is better than the BYM model in general.

1. 引言

新冠肺炎大流行历经三年，其中较为严重的是前两年的初始毒株和Delta大流行，通过贝叶斯时空模型可以良好地探索新冠肺炎在时间和空间维度上的发展趋势。对疾病的时空数据进行探索分析，这有助于我们知晓某种流行病的时空演变特征 [1] ，而对2020~2021新冠大流行的研究也是这个范畴。

BYM (Besag-York-Mollie)模型、FBM (Familiar Bayesian Spatio-temporal)模型是两种经典的贝叶斯时空统计模型，BYM模型是当前使用较多的、被充分验证过的贝叶斯时空统计模型，由Besag等人提出 [2] ，而FBM模型是G. Li等以BYM为根基而发展出的一种模型 [3] ，本文的后续讨论采用这两种模型。这两种模型目前已经被广泛运用于分析时空演变的问题当中，包括疾病、犯罪等问题的风险评估，例如，于国伟等利用BYM模型分析了甘肃省武威市凉州区胃癌死亡的时空分布及演变 [4] ，潘蕾等采用BYM模型分析了北京市2005~2009各区的结核病在气温、人口等影响因子的作用下的时空演变特征 [5] ，张伟文等运用BYM模型分析了新疆涂阳地区的肺结核发病的时空演变 [6] ，Daiane Leite da Roza等以BYM模型分析了巴西东南部São Paulo州Ribeirão Preto结核病发病率的时空格局及其与社会脆弱性的关系 [7] ，Daqian Liu等用BYM模型，加入相应的分析参数，基于贝叶斯时空模型研究了长春市犯罪时空格局 [8] ，上述研究的问题都有两个特点，那就是研究的对象都具有时间性和空间性两个性质，对于本文的研究很有借鉴价值，因而我们可以尝试将BYM模型应用于新冠肺炎的研究。FBM模型起初由G. Li等提出并运用于英国彼得区的入室盗窃犯罪风险评估，并分析了该区域内的热点、冷点区域及其发展趋势 [9] ，Danyan Liang等采用FBM模型讨论了2010~2015年内蒙古地区的布鲁氏菌疫情的时空发展演变 [10] ，Li Wang等运用FBM模型分析了社会经济发展不平衡地区的结核病的时空演变 [11] ，Ram K. Raghavan等采用FBM模型论证了美国落基山脉特有的斑点热疾病的时空分布和演变，并评估其风险，同时探讨了相关的驱动因素 [12] ，Junming Li等使用该方法分析论证了中国大陆地区卫生支出的时空演变并探讨了驱动因素以及驱动因素对演变的影响程度 [13] ，Xiangxue Zhang等采用该方法分析了2000~2018年中国PM2.5与气象和社会经济因素的时空异质性 [14] ，Wei Wang等运用FBM模型探索了2006~2020年中国大陆2844个县心血管死亡率的时空趋势和生态决定因素 [15] ，同样通过上述文献的论述，我们可以看出凡是研究对象具有时间和空间两个维度的属性，分析其时空发展的趋势可以采用FBM模型，新冠原始毒株和Delta的大流行在空间上，新冠流行于全世界，时间上跨越三年，因而将FBM模型应用于新冠肺炎的风险评估，分析其时空发展趋势也是符合条件的。那么两种模型在分析评估COVID-19问题当中的应用结果如何？通过上述前人的研究我们发现贝叶斯时空模型被较少地应用于新冠大流行的研究中，同时驱动一个地区新冠流行的影响因子对新冠流行风险的影响程度鲜有系统地评估；而且BYM与FBM模型的优劣对比也鲜有提及。因此，本文以2020~2021年河南省地区的新冠肺炎疫情作为研究对象，探讨两种模型在该流行病学研究中的应用情况和模型对比的结果,同时探索研究该流行病的驱动因素及其对疾病风险的影响。这里我们采用离差信息准则(Deviance Information Criterion, DIC)来比较两种模型之间的拟合程度，评价模型在应用中的优劣，一般DIC值越小模型拟合情况越佳 [16] 。

2. 理论分析

2.1. 数据相关性及因子分析

首先，对2020~2021年河南省18个地级市的各影响因子、确诊人数的数据取平均值，而后对各潜在的影响因子同确诊人数做相关性分析，这里采用皮尔逊相关性分析的方法，公式如下：

$r_{ij}=\frac{{\displaystyle \sum \left(x-\bar{x}\right)\left(y-\bar{y}\right)}}{\sqrt{{\displaystyle \sum {\left(x-\bar{x}\right)}^2}{\displaystyle \sum {\left(y-\bar{y}\right)}^2}}}$ (1)

得出结果后对相关性系数进行检验，得出结果P值小于0.05具有统计学意义，大于0.05不具有统计学意义，予以舍弃，从而筛选出合适的影响因子。

完成相关性分析后，对筛选完成的影响因子进行因子分析。由于各个影响因子在单位及量纲上都不一致，因而需要对各影响因子进行归一化，从而方便后续的建模分析。归一化的方法公式如下：

$\text{Normalization-Index}=\frac{X_{kij}-\text{Min}}{\text{Max}-\text{Min}}$ (2)

其中， $X_{kij}$ 表示区域i第j年第k个变量的原始数据，Min表示第k个变量的最小值，Max表示第k个变量的最大值，Normalization-Index的取值范围是0~1。

为使各影响因子间消除共线性问题，这里采用因子分析对指标间进行降维，从而对各影响因子进行新的分类重组。运用Bartlett球度检验和KMO检验，检查变量是否独立或相关，Bartlett球度检验统计量设为0.05，KMO取值介于0~1之间，取值越接近1，则变量间的相关程度越强，KMO统计量大于0.7以上时，因子分析效果较好。因子分析的数学模型表达如下：

$X=\{\begin{array}{l}{X}_1=a_{11}{F}_1+a_{12}{F}_2+\cdots +a_{1m}{F}_m+{\epsilon }_1\\ ⋮\\ X_n=a_{n1}{F}_1+a_{n2}{F}_2+\cdots +a_{nm}{F}_m+{\epsilon }_n\end{array}=AF+\epsilon$ (3)

2.2. 贝叶斯时空模型的构建

BYM和FBM模型均是利用先验分布对模型中所有的未知参数进行描述，随后进行贝叶斯估计获得贝叶斯后验分布，并利用马尔科夫蒙特卡洛方法(MarkovChain Monte Carlo methods, MCMC)进行后验分布的计算，最终获得未知参数的估计值 [17] 。

2.2.1. BYM模型的构建

设区域i在j时间段内感染病例数为 $Y_{ij}$ ，当感染人数远小于当地标准人口数时，可以认为 $Y_{ij}$ 服从Poisson分布。

$Y_{ij}|p_{ij}~\text{Poisson}\left(e_{ij}{\theta }_{ij}\right)$ (4)

$e_{ij}=n_{ij}\ast \left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{Y}_{ij}}/{\displaystyle \underset{i=1}{\overset{n}{\sum }}{n}_{ij}}\right)$ (5)

${\theta }_{ij}=\exp \left({\alpha }_0+{\mu }_i+g_j+Ps{i}_{ij}+v_i+{\alpha }_1\ast time{1}_j+d_i\ast time{1}_j+{\displaystyle \sum {\beta }_k\ast x_{kij}}\right)$ (6)

其中 $p_{ij}$ 表示区域i在j时间段内的感染率， $e_{ij}$ 是区域i在j时间段内的预期感染人数， $n_{ij}$ 为区域i在j时间段内的标准人口数。 ${\theta }_{ij}$ 是区域i在第j年的相对风险度。 ${\alpha }_0$ 表示截距， ${\mu }_i$ 表示空间同质性， $v_i$ 表示空间异质性， $g_j$ 表示自回归时间效应， ${\alpha }_1$ 表示时问效应的系数， $time{1}_j$ 表示第j年的时间效应， $d_i$ 表示距离效应， $Ps{i}_{ij}$ 表示时空交互效应， ${\beta }_k$ 表示相应影响因子的协变量， $x_{kij}$ 表示区域i第j年的第k个影响因子。

空间同质性 ${\mu }_i$ 反映空间相关性，其先验信息一般通过条件自回归模型(Conditional Autoregressive Process, CAR)建模表示。模型公式如下：

${\mu }_i|{\mu }_{j,j\ne i}~N\left({\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{w}_{ij}{\mu }_j},{\sigma }_{\mu }^2/n_i\right)$ (7)

其中， ${\mu }_i|{\mu }_{j,j\ne i}$ 表示区域i和区域j之间的空间效应； ${\sigma }_{\mu }^2/n_i$ 代表区域i受到相邻m个区域空间效应影响

的方差平均值， ${\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{w}_{ij}{\mu }_j}$ 代表区域i受到相邻m个单位空间效应影响的平均值，这里我们探寻的是河南省

18个地级市的空间同质性，所以，若两地市相邻则令 $w_{ij}=1$ ，反之则等于0。空间异质性由空间非结构效应反映，一般通过正态分布建模，即：

$v_i~N\left(0,{\sigma }_v^2\right)$ (8)

时间效应、时空交互效应一般也通过正态分布建模，而距离效应的建模方法与空间同质性的建模方法相同。这里所有的参数的超先验分布均采用标准差为(0, 10)的均匀分布，对于截距 ${\alpha }_0$ 的先验分布，这里采用无信息先验分布。

2.2.2. FBM模型的构建

FBM的数学形式如下：

${\theta }_{ij}=\exp \left({\alpha }_0+s_i+b_0{t}^{*}+v_j+b_{1i}{t}^{*}+{\epsilon }_{ij}+{\displaystyle \sum {\beta }_k{x}_{kij}}\right)$ (9)

$s_i=\exp \left({\alpha }_1+{\mu }_i+v_i\right)$ (10)

$t^{*}=t-t_{mean}$ (11)

这里， ${\alpha }_0$ 表示截距， $s_i$ 表示疾病风险的空间分布，这部分可以用BYM模型来表示。( $b_0{t}^{*}+v_j$ )代表在各区域里共同的时间变化趋势， $b_0{t}^{*}$ ( $t^{*}=t-t_{mean}$ )代表共同的时间趋势中线性组成部分， $v_j$ 通过正态分布建模代表时间效应中的随机变化部分。 $b_{1i}{t}^{*}$ 代表各区域各自的独立的时间变化趋势； ${\epsilon }_{ij}$ 代表不包含在模型中但是对观测数据产生影响的随机误差项。 ${\beta }_k$ 表示相应影响因子的协变量， $x_{kij}$ 表示区域i第j年的第k个影响因子。各参数采用正态分布建模，各参数的超先验分布采用方差(0, 10)的均匀分布； ${\mu }_i$ 和 $v_i$ 的先验分布与BYM模型相同； $b_0$ 、 $b_{1i}$ 的取值通过计算河南省整体确诊人数变化率和各地级市确诊人数变化率获得。本文中的两种模型均在WinBUGS1.4中编译运行。

3. 实证分析

3.1. 数据来源

2020~2021年河南省新冠肺炎确诊人数数据来源于河南省疾病预防控制中心，诸影响因子来源于2020年和2021年河南省统计年鉴。共引入GDP、农林牧渔产值、工业产值、建筑业产值、批发零售产值、交通运输产值、住宿餐饮产值、金融产值、房地产产值、其他服务业产值、居民人均家庭收入、第一产业单位数、第二产业单位数、第三产业单位数、年平均空气质量指数(AQI)、年平均气温、年平均降水、医疗机构、医疗床位数、医疗人员数共计20个影响因子。河南省基础地理信息数据来源于天地图。

3.2. 相关性及因子分析

将确诊人数和各感兴趣的影响因子进行两两相关性分析，分析结果如图1：

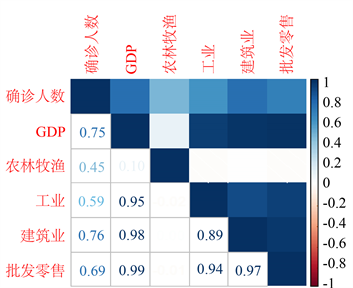
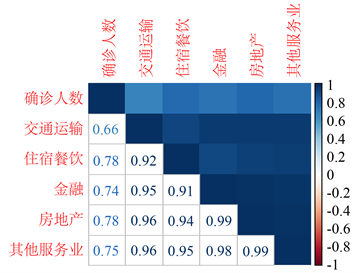
Figure 1. Correlation analysis of the number of diagnosed patients with each influence factor

图1. 确诊人数同各影响因子的相关性分析

相关性分析完成后，我们对结果进行检测，检测结果见表1。

通过上述分析，我们可以发现GDP、工业、建筑业、批发零售、交通运输、金融、其他服务业、第二产业单位数、医疗机构的P值大于0.05，不具备统计学意义，故而舍弃上述影响因子。筛选后的影响

Table 1. Results of correlation analysis between the number of confirmed diagnoses and each impact factor indicator detection

表1. 确诊人数与各影响因子指标相关性分析结果检测

因子，显然平均AQI、平均气温、平均降水属于气象因子，其余属于社会经济因子，分成两组进行因子分析，分析结果如下：

Table 2. Test results of socio-economic and meteorological factors

表2. 社会经济因子和气象因子的检验结果

从表2的分析结果看，社会经济因子的KMO值大于0.7，且显著性小于0.001，适合进行因子分析，而气象因子的KMO值小于0.7，且显著性大于0.001，故而不适合进行因子分析。所以，对社会经济因子进行因子分析，对其进一步降维，而气象环境因子中的平均气温、平均AQI、平均降水我们则将其设定为三个独立变量代入后面的贝叶斯统计建模中。社会经济因子的降维如图2、表3：

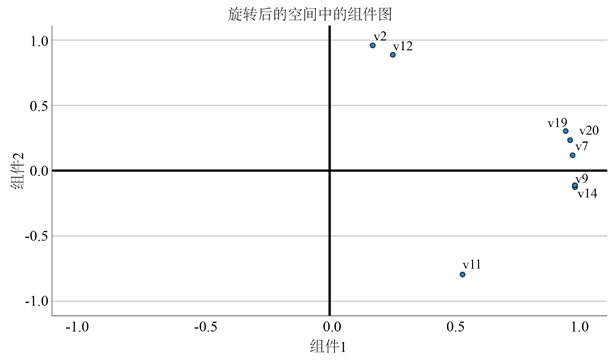
Figure 2. Spatial component diagram after rotation

图2. 旋转后的空间组件图

Table 3. Component score coefficient matrix

表3. 成分得分系数矩阵

这里V2代表农林牧渔业，V7代表住宿餐饮业，V9代表房地产，V11代表居民人均家庭收入，V12代表第一产业单位数，V14代表第三产业单位数，V19代表医疗床位数，V20代表医疗人员数。根据分析结果，这八个影响因子可以分成两个部分，第一部分包含农林牧渔业、居民人均家庭收入和第一产业单位数这三个影响因子，将这一部分命名为基础经济因子；其余为第二部分，将其命名为社会因子。至此，我们完成了数据的相关性分析和因子分析。

3.3. 贝叶斯时空模型建模

3.3.1. BYM建模

假设河南省地级市i第j年的相对风险为 $r{r}_{ij}$ ，基础经济因子为 $x_{1ij}$ ，社会因子为 $x_{2ij}$ ，平均AQI为 $x_{3ij}$ ，平均气温为 $x_{4ij}$ ，平均降水为 $x_{5ij}$ ，各影响因子的协变量系数为 ${\beta }_1~{\beta }_5$ 。那么构建的BYM数学模型如下：

$Y_{ij}|p_{ij}~\text{Poisson}\left(e_{ij}r{r}_{ij}\right)$

$r{r}_{ij}=\exp \left({\alpha }_0+{\mu }_i+g_j+Ps{i}_{ij}+v_i+{\alpha }_1\ast time{1}_j+d_i\ast time{1}_j+{\beta }_1\ast x_{1ij}+{\beta }_2\ast x_{2ij}+{\beta }_3\ast x_{3ij}+{\beta }_4\ast x_{4ij}+{\beta }_5\ast x_{5ij}\right)$

在WinBUGS1.4中进行大约300000次迭代，模型基本达到了收敛状态。

模型达到收敛后，我们可以得出河南省18个地级市2020年和2021年的相对风险程度的平均数值(见表4)，同时可以得出五个影响因子对相对风险的影响评估(见表5)。

Table 4. Relative risk level of prefecture-level cities in Henan Province, 2020~2021 in BYM Model

表4. BYM模型下2020~2021年河南省各地级市相对风险程度

Table 5. Impact assessment of each impact factor in BYM Model

表5. BYM模型下各影响因子的影响评估

根据表4的结果，绘制河南省2020~2021年新冠肺炎疾病风险专题地图，见图3、图4：

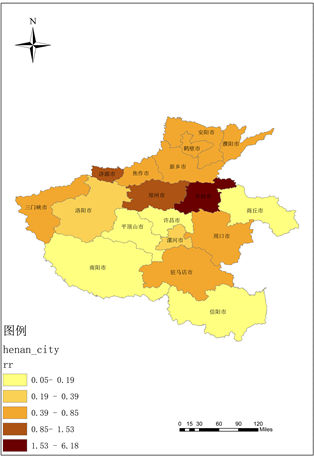
Figure 3. Risk assessment map of COVID-19 epidemic by prefecture-level cities in Henan Province in 2020 (BYM)

图3. 2020年河南省各地级市新冠疫情风险评估图(BYM)

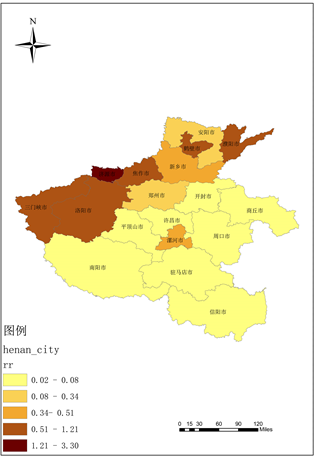
Figure 4. Risk assessment map of COVID-19 by prefecture-level cities in Henan Province in 2021 (BYM)

图4. 2021年河南省各地级市新冠疫情风险评估图(BYM)

从表5的结果来看，农林牧渔业、第一产业单位数等基础经济因子对新冠疫情的影响是正相关的，而空气质量指数即平均AQI对新冠疫情也存在着正相关的影响，且其中社会因子和平均气温对新冠疫情的影响较大，而从图3、图4的专题地图的表现来看，风险程度较高的主要集中于河南的中北部地区。河南的经济发达地区主要集中于这里，这里位于华北平原，农林牧渔业等基础经济因子也相较发达，同时，这里有着河南重要的工业基地，所以空气质量相对南部城市较差，人口也相对集中，所以疫情的风险集中于此。

3.3.2. FBM建模

假设河南省地级市i第j年的相对风险为 $r{r}_{ij}$ ，基础经济因子为 $x_{1ij}$ ，社会因子为 $x_{2ij}$ ，平均AQI为 $x_{3ij}$ ，平均气温为 $x_{4ij}$ ，平均降水为 $x_{5ij}$ ，各影响因子的协变量系数为 ${\beta }_1~{\beta }_5$ 。那么构建的FBM数学模型如下：

$Y_{ij}|p_{ij}~\text{Poisson}\left(e_{ij}r{r}_{ij}\right)$

$r{r}_{ij}=\exp \left({\alpha }_0+s_i+b_0{t}^{*}+v_j+b_{1i}{t}^{*}+{\epsilon }_{ij}+{\beta }_1\ast x_{1ij}+{\beta }_2\ast x_{2ij}+{\beta }_3\ast x_{3ij}+\beta \ast x_{4ij}+{\beta }_5\ast x_{5ij}\right)$

$s_i=\exp \left({\alpha }_1+{\mu }_i+v_i\right)$

在WinBUGS1.4中迭代400,000次，初始值burn in设置为10,000，模型基本达到收敛，这里 $t^{*}=t-t_{mean}$ ，t取1，2，则 $t_{mean}=1.5$ 。

模型达到收敛后，我们可以得出河南省18个地级市2020年和2021年的相对风险程度的平均数值(见表6)，同时可以得出五个影响因子对相对风险的影响评估(见表7)。根据表4的结果绘制河南省各地级市2020~2021年新冠疫情专题地图，见图5，图6，同时我们用WinBUGS1.4软件计算BYM和FBM两模型的DIC值，见表8。

Table 6. Relative risk level of prefecture-level cities in Henan Province, 2020~2021 in FBM Model

表6. FBM模型下2020~2021年河南省各地级市相对风险程度

Table 7. Impact assessment of each impact factor in FBM Model

表7. FBM模型下各影响因子的影响评估

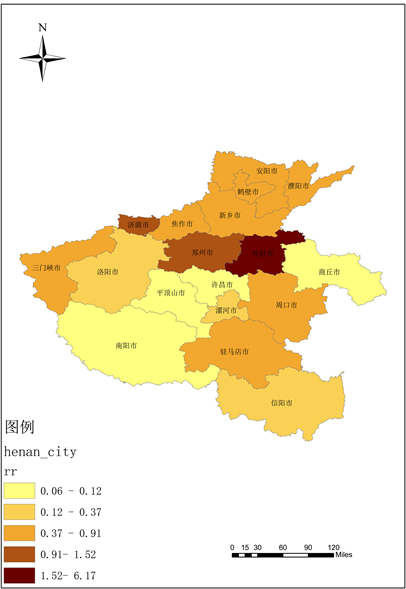
Figure 5. Risk assessment map of COVID-19 epidemic by prefecture-level cities in Henan Province in 2020 (FBM)

图5. 2020年河南省各地级市新冠疫情风险评估图(FBM)

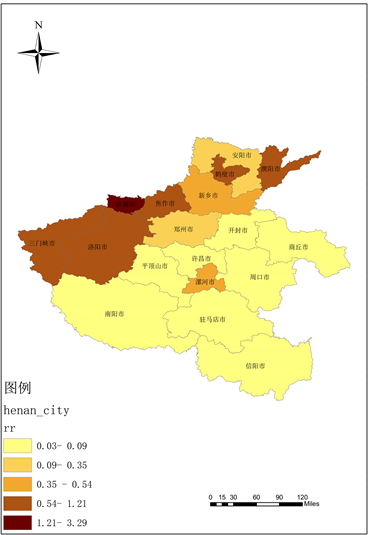
Figure 6. Risk assessment map of COVID-19 epidemic by prefecture-level cities in Henan Province in 2021 (FBM)

图6. 2021年河南省各地级市新冠疫情风险评估图(FBM)

Table 8. Comparison of the fit of the two models

表8. 两种模型的拟合程度比较

注：DIC = Dbar + pD。

从最终的结果来看，基础经济因子、社会因子以及平均降水是对河南省新冠疫情的影响较大的影响因素，各影响因子都对相对风险存在正相关的影响，相对风险的程度都会随着各影响因子的指标的提升而提升。从两年的河南省各地级市的疫情风险评估专题地图也可以看出，河南省各地级市的新冠疫情相对风险程度呈现整体的下降趋势，在河南的北部地区新冠疫情的风险一直较为严重，其中济源市、三门峡市、洛阳市、焦作市、濮阳市、鹤壁市在2021年的疫情相对风险程度有所增加，郑州市略微减弱。而河南南部的城市，从2020年到2021年全部都成减弱趋势。

4. 结论

本文采用的BYM和FBM模型，通过2020~2021年河南省新冠疫情时空风险评估的应用，我们可以得出结论如下：

2020~2021年的新冠大流行的风险评估可以运用BYM和FBM来实现，同时我们运用这两种模型还可以分析出相应的影响因子的影响系数。从两种模型最终的分析结果来看，2020~2021年河南省新冠疫情较为严重的城市主要集中于河南的北方，从时空发展的趋势来看，从东北部向西北部转移。南部地区在大流行的第二年基本上风险系数都降低到了较低值。从两个模型中影响新冠大流行风险的影响因子评估结果来看，基础经济因子和社会因子是影响程度较大的。从数据上看，河南省的主要产业集中于以郑州为中心的城市群，这里也是河南省人口稠密的地区，所以可以说这里的风险较大是符合实际情况的。这表明BYM和FBM两种模型不仅可以良好地评估研究区域的风险程度，而且可以良好地分析影响因子的对大流行风险的影响程度。

对于BYM模型和FBM模型的优劣对比，通过表6的DIC值计算结果可以明显看出，FBM模型是优于BYM模型。同时，通过对影响因子的评估结果分析我们可以看出，FBM模型的分析结果更加符合实际，在2021年河南省因为发生了强降水导致了较大范围的洪灾，洪灾过后疫情加重，这说明降水对于新冠大流行的风险有着较大的影响，而BYM模型的评估结果中，平均降水的影响系数仅为0.49，同时，气温对于新冠大流行的影响已然被证明影响程度有限，而BYM分析出的影响系数确是1.27，对比FBM模型仅为0.34，因而我们认为FBM模型对于新冠大流行风险的时空分析更为准确。

本文以河南省2020~2021年新冠疫情为例，探索了可能影响新冠大流行风险的影响因子，并探索了用BYM和FBM模型对新冠疫情的分析评估，并对比两种模型的优劣。最终证明，新冠疫情作为具有空间流行病特点的研究对象，可以运用贝叶斯时空模型来分析处理，同时在相同数据的前提下，FBM模型的分析结果要优于BYM模型。

NOTES

^*通讯作者。