针对全球变暖问题的相关数据的建模量化分析

Modeling Quantitative Analysis of Data Related to the Problem of Global Warming

摘要: 本文旨在针对自上个世纪开始出现的全球变暖效应，在进入21世纪后出现了Hiatus (全球变暖停滞状态)现象，使得公众开始怀疑全球变暖的真实性这一具体情况，通过大量数据分析全球变暖产生的原因，深入挖掘并量化分析极端天气现象的产生原因与气候变化之间所存在的数学关系，通过具体国家，选取代表性城市通过历史数据挖掘出温度的时空变化趋势，从历史数据中找寻温度变化规律。同时本文站在气候尺度上看待全球变暖问题，考虑到地表温度变化、大气层中二氧化碳浓度变化以及海洋吸热等一系列因素，量化相关数据，建立有利于非专业人士理解和认识的全球气候模型和极端天气模型，对未来气候变化进行预测。

Abstract: The purpose of this paper is to address the specific situation that Hiatus (global warming hiatus) phenomenon has appeared since the last century, which makes the public begin to doubt the reality of global warming. Through analyzing the causes of global warming with a large number of data, the mathematical relationship between the causes of extreme weather phenomena and climate change is deeply explored and quantitatively analyzed. Through the historical data of specific countries and representative cities, the temporal and spatial trends of temperature are mined, and the rules of temperature change are found from the historical data. At the same time, this paper looks at global warming from the climate scale, taking into account a series of factors such as surface temperature change, carbon dioxide concentration change in the atmosphere and ocean heat absorption, quan-tifying relevant data and establishing global climate models and extreme weather models that are conducive to non-professionals’ understanding and cognition, so as to predict future climate change.

1. 引言

从工业革命开始，由于大气中的二氧化碳浓度不断上升，温室效应的效果也随之增强。由于存在温室效应，影响地气系统吸收与发射的能量平衡，能量不断在地气系统累积，从而导致温度上升，造成全球气候变暖，不仅会危害自然生态系统的平衡，还威胁人类的生存。虽然温室气体的浓度在不断上升，但自从进入21世纪以来，10年间全球全年平均气温上升率仅为0.03℃，几乎未变化，这种现象叫做Hiatus (全球变暖停滞状态)。正因为出现全球变暖停滞现象，使公众对全球变暖产生了怀疑。2019年1月美国2/3的地区变成了一个大冰窖，出现了“几十年一遇”的极度寒冷天气，成为有人怀疑全球变暖的依据之一。导致分歧的原因在于观察问题的角度和范围。全球变暖是在气候尺度上看全球问题。从气候角度研究全球温度变化需要全球范围长时间的观测积累，但过去这方面的时空数据并不完整，给统计计算带来极大困难。不仅如此，海洋吸收热量对全球气候变化的影响很大。观测发现海洋表面温度的变化具有某种震荡特征，如年代际太平洋震荡、厄尔尼诺现象、拉尼娜现象等。这些因素使得研究全球温度变化更加困难。

吕金莹等 [1] 运用差分整合移动平均自回归模型(ARIMA)对松嫩平原未来10年活动积温变化进行了预测。周宏伟等 [2] 运用自回归移动平均模型(ARMA)对北京月平均相对温度进行了预测。薛宇峰和杨超梅 [3] 利用墨西哥帽小波函数分析了近百年来全球气温的变化特征，并用气温距平序列的5a滑动平均计算了信噪比(S/N)，验证了气候突变点的位置，同时，利用人工神经网络对全球气温变化趋势进行了的预测。彭润龙等 [4] 综合分析了全球变暖的气候变化问题对全球变暖背景下海洋表面温度的规律变化，对未来25年的气候变化进行了预测，并就极端天气现象与气候变化的影响因素建立了多元回归分析模型进行研究。

一般系统理论只能建立差分模型，不能建立微分模型。针对上述问题，本文采用了灰色理论 [5] 的微分方程性模型称为GM模型。差分模型是一种递推模型，只能按阶段分析系统的发展，只能用于短期分析，只能了解系统显露的变化。而灰色理论，基于关联度收敛原理、生成数、灰导数、灰微分方程等观点和方法建立了微分方程型模型。这样建立的模型，适用性强，计算方便，结果精确，可以实现对杂乱无章的原始数据的处理。加拿大是世界上海岸线最长的国家，气候情况复杂。本文选取五个具有气候代表性的城市，对其近35年的温度变化，降雨和降雪量进行数据分析，挖掘出加拿大温度时空变化趋势。观察其温度周期波动情况，并建立GM模型预测未来25年的气候变化。

2. 基本假设和符号说明

2.1. 基本假设

假设一：针对本文官网提供的数据均为真实有效的数据；

假设二：地球以外的因素不会对所建立的地球气候模型产生影响；

假设三：各种社会因素处于稳定状态。假设地球整体环境处于稳定状态；

假设四：假设加拿大的年平均温度变化趋势与全球表面温度变化趋势一致。

2.2. 符号说明

本文用到的符号以及其意义如表1所示。

Table 1. Description of some symbols used in this article

表1. 本文用到的部分符号说明

3. 模型建立及求解

3.1. 大气二氧化碳含量数据

大气中能产生温室效应的气体近30种，其中二氧化碳起重要的作用，从长期气候数据比较来看，在气温和二氧化碳之间存在显著的相关关系。本文采用世界气象组织发布的温室气体公报中全球二氧化碳浓度进行分析(表2)。

Table 2. Global average carbon dioxide concentration

表2. 全球二氧化碳平均浓度

3.2. 模型建立和求解

采用GM(1,n)模型，设时间序列 $X^{\left(0\right)}=\left\{X^{\left(0\right)}\left(1\right),X^{\left(0\right)}\left(2\right),\cdots ,X^{\left(0\right)}\left(n\right)\right\}$ 有n个观察值，通过累加生成新序列 $X^{\left(1\right)}=\left\{X^1\left(1\right),X^1\left(2\right),\cdots ,X^1\left(n\right)\right\}$ 则GM(1,n)模型相应的白化形式微分方程为：

$\frac{\text{d}{X}^{\left(1\right)}}{\text{d}t}+a{X}^{\left(1\right)}=\mu$ (1)

其中：α称为发展灰数；μ称为内生控制灰数。

记

$B=\left(\begin{array}{cc}-\frac{1}{2}\left[X^{\left(1\right)}\left(1\right)\text{+}{X}^{\left(1\right)}\left(2\right)\right]& 1\\ -\frac{1}{2}\left[X^{\left(1\right)}\left(2\right)\text{+}{X}^{\left(2\right)}\left(3\right)\right]& 1\\ \cdots & \\ -\frac{1}{2}\left[X^{\left(1\right)}\left(n-1\right)\text{+}{X}^{\left(1\right)}\left(n\right)\right]& 1\end{array}\right)$

$Y_n=(\begin{array}{c}{X}^{\left(0\right)}\left(2\right)\\ X^{\left(0\right)}\left(3\right)\\ \cdots \\ X^{\left(n\right)}(\; n\; ))\end{array}$

称 $Z^{\left(1\right)}$ 为 $X^{\left(1\right)}$ 的紧邻均值生成序列

$Z^{\left(1\right)}\text{=}\left\{Z^1\left(2\right),Z^1\left(3\right),\cdots ,Z^1\left(n\right)\right\}$

$Z^{\left(1\right)}\left(k\right)\text{=}\frac{1}{2}(X^{\left(1\right)}\left(k-1\right)+X^{\left(1\right)}(\; k\; ))$

则

$B=\left(\begin{array}{cc}-Z^{\left(1\right)}\left(2\right)& 1\\ -Z^{\left(1\right)}\left(3\right)& 1\\ \cdots & \\ -Z^{\left(1\right)}\left(n\right)& 1\end{array}\right)$

设 $\hat{\alpha }$ 为待估参数向量， $\hat{\alpha }=(\; a\; \mu \; )$

则微分方程可表示为

$Y=B\hat{\alpha }$ (2)

可利用最小二乘法求解，解得：

$\hat{\alpha }={\left(B^{\text{T}}B\right)}^{-1}{B}^{\text{T}}{Y}_n$ (3)

求解微分方程，即可得预测模型：

${\hat{X}}^{\left(1\right)}\left(k+1\right)=\left[X^{\left(0\right)}\left(1\right)-\frac{\mu }{a}\right]{\text{e}}^{-ak}+\frac{\mu }{a}，k=0,1,2,\cdots ,n.$ (4)

对其做累减还原，即可得到原始数列的灰色预测模型为：

${\hat{X}}^{\left(0\right)}\left(k\right)={\hat{X}}^{\left(1\right)}\left(k+1\right)-{\hat{X}}^{\left(1\right)}\left(k\right)$ (5)

由灰色预测方法原理，−a主要控制系统发展态势的大小，即反映预测的发展态势，被称为发展系数；μ的大小反映了数据变化的关系，被称为灰色作用量，其中：

①当−a < 0.3时，GM(1,1)模型可用于中长期预测；

②当0.3 < −a < 0.5时，GM(1,1)模型可用于短期预测，中长期预测慎用；

③当0.5 < −a < 1时，应采用GM(1,1)改进模型，包括GM(1,1)残差修正模型；

④当−a > 1时，不宜采用GM(1,1)模型，可考虑其他预测方法。

模型检验一般有残差检验、关联度检验和后验差检验。

1) 残差检验

按预测模型计算 ${\hat{X}}^{\left(1\right)}\left(i\right)$ ，将 ${\hat{X}}^{\left(1\right)}\left(i\right)$ 累减生成 ${\hat{X}}^{\left(0\right)}\left(i\right)$ ，然后计算原始数列 $X^{\left(0\right)}\left(i\right)$ 与 ${\hat{X}}^{\left(0\right)}\left(i\right)$ 的绝对误差序列及相对误差序列。

${\Delta }^{\left(0\right)}\left(i\right)=\left|X^{\left(0\right)}\left(i\right)-{\hat{X}}^{\left(0\right)}\left(i\right)\right|,i=1,2,\cdots ,n$ (6)

$\Phi \left(i\right)=\frac{{\Delta }^{\left(0\right)}\left(i\right)}{X^{\left(0\right)}\left(i\right)}\times 100\%,i=1,2,\cdots ,n$ (7)

给定a，当 $\bar{\Phi }<a$ 成立，称模型为残差合格模型

a取0.01、0.05、0.1分别为：优、合格、勉强合格

2) 关联度检验

根据前面所述关联度的计算方法算出 ${\hat{X}}^{\left(0\right)}\left(i\right)$ 与原始序列 $X^{\left(0\right)}\left(i\right)$ 的关联系数，然后计算出关联度，根据经验，当ρ = 0.5时，关联度大于0.6便满意了。

设原始数据序列 $X_0^{\left(0\right)}=\left\{x_0^{\left(0\right)}\left(1\right),x_0^{\left(0\right)}\left(2\right),\cdots ,x_0^{\left(0\right)}\left(n\right)\right\}$ 为参考序列，用m种灰色建模得模型值分别为 $X_i^{\left(0\right)}=\left\{x_i^{\left(0\right)}\left(1\right),x_i^{\left(0\right)}\left(2\right),\cdots ,x_i^{\left(0\right)}\left(n\right)\right\}$ ， $i=1,2,\cdots ,m$ ，求出该点m个序列与参考序列的邓氏关联度 ${\epsilon }_i\left(i=1,2,\cdots ,m\right)$ ，如果 ${\gamma }_i\left(i=1,2,\cdots ,m\right)$ 在所有关联度中最大，则第i种灰色建模方法为所建模型中最好的模型。

3) 后验差检验

a) 计算原始序列标准差：

$S_1=\sqrt{\frac{{\displaystyle \sum {\left[X^{\left(0\right)}\left(i\right)-{\bar{X}}^{\left(0\right)}\right]}^2}}{N}}$ (8)

b) 计算绝对误差序列的标准差：

$S_2=\sqrt{\frac{{\displaystyle \sum {\left[{\Delta }^{\left(0\right)}\left(i\right)-{\bar{\Delta }}^{\left(0\right)}\right]}^2}}{N}}$ (9)

c) 计算方差比：

$C=\frac{S_2}{S_1}$ (10)

d) 计算小误差概率：

$P=P\left\{\left|{\Delta }^{\left(0\right)}\left(i\right)-{\bar{\Delta }}^{\left(0\right)}\right|<0.6745S_1\right\}$ (11)

令

$e_i=\left|{\Delta }^{\left(0\right)}\left(i\right)-{\bar{\Delta }}^{\left(0\right)}\right|,S_0=0.6745S_1$

则

$P=P\left\{e_i<S_0\right\}$ (12)

若相关误差，关联度、后验差检验在允许范围之内，则可用所建模型进行预测(表3)。

Table 3. Accuracy class

表3. 精度等级

3.3. 灰色关联度分析介绍

灰色系统的应用范畴大致分为：灰色关联分析、灰色预测、灰色决策、灰色预测控制。灰色系统理论是人们认识客观系统改造客观系统的一个新型的理论工具。灰色关联分析有别于过去主要采取回归分析、方差分析，主成分分析的因素分析方法，灰色系统理论采用的关联分析方法可以克服过去算法需要大量数据作为基础，计算量大的弊端。

利用灰色关联分析进行综合评价的步骤是：

1) 确定评价指标体系，收集评价数据。

设n个数据序列形成如下矩阵：

$\left({X^{\prime }}_1,{X^{\prime }}_2,\cdots ,{X^{\prime }}_n\right)=(\begin{array}{cccc}{x^{\prime }}_1\left(1\right)& {x^{\prime }}_2\left(1\right)& \cdots & {x^{\prime }}_n\left(1\right)\\ {x^{\prime }}_1\left(2\right)& {x^{\prime }}_2\left(2\right)& \cdots & {x^{\prime }}_n\left(2\right)\\ ⋮& ⋮& ⋮& ⋮\\ {x^{\prime }}_1\left(m\right)& {x^{\prime }}_2\left(m\right)& \cdots & {x^{\prime }}_n(\; m\; ))\end{array}$

其中m为指标的个数，

${X^{\prime }}_i={\left({x^{\prime }}_i\left(1\right),{x^{\prime }}_i\left(2\right),\cdots ,{x^{\prime }}_i\left(m\right)\right)}^{\text{T}},i=1,2,\cdots ,n.$

2) 确定参考数据列

参考数据列应该是一个理想的比较标准，可以以各指标的最优值(或最劣值)构成参考数据列，也可根据评价目的选择其它参照值。记作

${X^{\prime }}_0={\left({x^{\prime }}_0\left(1\right),{x^{\prime }}_0\left(2\right),\cdots ,{x^{\prime }}_0\left(m\right)\right)}^T$

3) 对指标数据进行无量纲化

无量纲化后的数据序列形成如下矩阵：

$\left(X_0,X_1,\cdots ,X_n\right)=(\begin{array}{cccc}{x}_0\left(1\right)& x_1\left(1\right)& \cdots & x_n\left(1\right)\\ x_0\left(2\right)& x_1\left(2\right)& \cdots & x_n\left(2\right)\\ ⋮& ⋮& ⋮& ⋮\\ x_0\left(m\right)& x_1\left(m\right)& \cdots & x_n(\; m\; ))\end{array}$

常用的无量纲化方法有均值化法、初值化法和 $\frac{x-\bar{x}}{S}$ 标准化变换等。

均值化法：

$x_i\left(k\right)=\frac{{x^{\prime }}_i\left(k\right)}{\frac{1}{m}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{x^{\prime }}_i\left(k\right)}},i=0,1,\cdots ,n\text{;}k=1,2,\cdots m.$ (13)

初值化法：

$x_i\left(k\right)\text{=}\frac{{x^{\prime }}_i\left(k\right)}{x_i\left(1\right)},i=0,1,\cdots ,n\text{;}k=1,2,\cdots m.$ (14)

或采用内插法使各指标数据取值范围(或数量级)相同。

4) 逐个计算每个被评价对象指标序列(比较序列)与参考序列对应元素的绝对差值

$\left|x_0\left(k\right)-x_i\left(k\right)\right|\left(k=1,2,\cdots ,m;i=1,2,\cdots ,n\right)$ ，

n为被评价对象的个数。

5) 确定两级最小差与两级最大差

两级最小差

$\underset{i=1}{\overset{n}{\min }}\underset{k=1}{\overset{m}{\min }}\left|x_0\left(k\right)-x_i\left(k\right)\right|$

两级最大差

$\underset{i=1}{\overset{n}{\max }}\underset{k=1}{\overset{m}{\max }}\left|x_0\left(k\right)-x_i\left(k\right)\right|$

6) 计算关联系数

${\eta }_i\left(k\right)=\frac{\underset{i}{\min }\underset{k}{\min }\left|x_0\left(k\right)-x_i\left(k\right)\right|+\rho \underset{i}{\max }\underset{k}{\max }\left|x_0\left(k\right)-x_i\left(k\right)\right|}{\left|x_0\left(k\right)-x_i\left(k\right)\right|+\rho \underset{i}{\max }\underset{k}{\max }\left|x_0\left(k\right)-x_i\left(k\right)\right|},k=1,2,\cdots ,m.$

式中ρ为分辨系数，在(0, 1)内取值，若ρ越小，关联系数间差异越大，区分能力越强，常ρ取0.5。

如果 $\left\{x_0\left(k\right)\right\}$ 为最优值数据列， ${\eta }_i\left(k\right)$ 越大，越好；

如果 $\left\{x_0\left(k\right)\right\}$ 为最劣值数据列， ${\eta }_i\left(k\right)$ 越大，越不好。

7) 计算关联度

对各评价对象(比较序列)分别计算其个指标与参考序列对应元素的关联系数的均值，以反映各评价对象与参考序列的关联关系，并称其为关联度，记为：

${\gamma }_i=\frac{1}{m}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{\eta }_{{}_i}\left(k\right)}$ (15)

8) 如果各指标在综合评价中所起的作用不同，可对关联系数求加权平均值即

${{\gamma }^{\prime }}_i=\frac{1}{m}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{W}_k\cdot {\eta }_i\left(k\right),}k=1,2,\cdots ,m.$ (16)

式中 $W_k$ 为各指标权重。

9) 依据各观察对象的关联度，进行排序，得出综合评价结果。

4. 模型求解

4.1. 求解结果分析

利用上述GM模型，通过现有全球二氧化碳平均浓度数据以及温度变化情况对未来25年不同因素影响下的温度变化进行了预测。

图1(a)为二氧化碳浓度的变化情况。小概率误差P = 1，方差比C = 0.0045，相对误差Q = 1.0399e⁻⁵，通过精度比较我们发现小概率误差P = 1 > 0.95，方差比C = 0.0045 < 0.35，相对误差Q = 1.0399e⁻⁵ < 0.95，模型精度达到一级。由此可见GM模型可适用于预测温度变化 [6] 。图1(b)为海洋温度和二氧化碳浓度两个因素影响情况下温度变化的情况。小概率误差P = 0.8143，方差比C = 0.3937，相对误差Q = 0.06024，通过精度比较发现小概率误差P = 0.8143 > 0.80，方差比C = 0.3937 < 0.50，相对误差Q = 0.06024 < 0.95，模型精度较高。图1(c)为海洋温度，全球二氧化碳浓度以及降雨量和降雪量多个因素的影响下温度变化的情况。可以看出GM模型预测精度等级会降低，GM模型不能像神经网络那样考虑多因素问题，但是它可以作为一个简单模型来预测未来25年的变化，有利于非专业的简单理解。通过对比可以发现二氧化碳浓度对全球的温度变化具有显著的影响，并且全球的温度变化依旧处于一个上升趋势。

Figure 1. Temperature change under the influence of different factors

图1. 不同因素影响下温度的变化

4.2. 结果检验分析

通过多因素耦合神经网络RBF对GM模型预测结果进行检验。

如图2所示红色的为实际对应的公式，蓝色为输入因素得到的预测结果，从拟合度计算结果来看，R² = 0.98，均方根误差RMSE = 13.74，平均相对误差为0.1185，预测精度较高。

Figure 2. Neural network regression prediction data

图2. 神经网络回归预测数据

如图3，由后续25年预测结果可以看出神经网络预测的结果基本与GM预测趋势一致，在海洋温度，全球二氧化碳浓度以及降雨量和降雪量多个因素影响下，全球温度将持续走高。

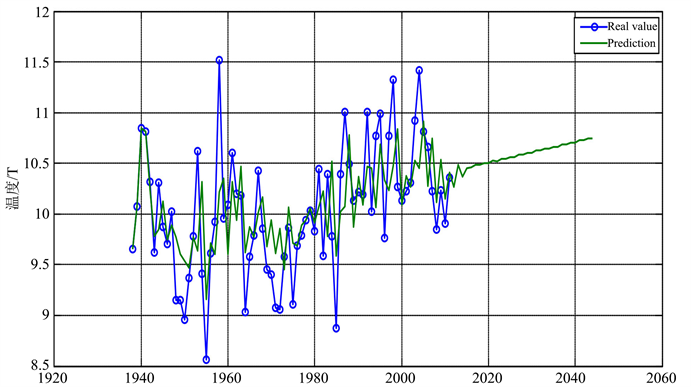
Figure 3. Forecast of temperature from 1938 to 2044

图3. 1938~2044年气温预测

5. 结论

从海温图中提取与经纬度有关的海温数据，收集全球二氧化碳浓度变化，将海温，加拿大五个站点的平均气温，全球二氧化碳的浓度作为变化要素从而建立简化的模型去预测未来25年的气候变化，所建立的模型区别于复杂的专业气候模型。在本文中采用GM模型通过单因素分析，多因素分析来观察模型的精度，在影响因素较少的情况下预测精度较高，在综合因素较多的情况下预测精度较低。最后采用神经网络RBF对GM模型预测的结果进行对比，验证得到预测结果基本一致。