基于改进的K-均值聚类算法构建柴油车运行工况

Construction of Diesel Vehicle Driving Condition Based on Improved K-Means Clustering Algorithm

摘要: 针对传统的K-均值聚类算法在聚类时容易陷入局部最优的问题，提出一种改进的K-均值聚类算法，并结合主成分分析法将其应用到柴油车运行工况的构建中。首先通过主成分分析完成运动学片段特征参数的降维，再利用改进的K-均值聚类算法进行运动学片段的聚类，最后选择具有代表性的片段合成运行工况。对自主构建的运行工况的特征参数值和总体数据的特征参数值进行比较，各参数间的相对误差在2%~5%之间，说明用改进后的K-均值聚类算法结合主成分分析法构建的运行工况具有很高的精度，并且对车辆的运行状况具有很强的代表性。

Abstract: Aiming at the problem that the traditional K-mean clustering algorithm is prone to fall into the local optimum during clustering, an improved K-mean clustering algorithm is proposed, and combined with the principal component analysis method, it is applied to the construction of diesel vehicle op-erating conditions. Firstly, dimensionality reduction of characteristic parameters of kinematic seg-ments was completed through principal component analysis, and then the improved K-means clus-tering algorithm was used to cluster kinematic segments. Finally, representative segments were selected to synthesize operating conditions. By comparing the characteristic parameter values of the independently constructed operating conditions with those of the overall data, the relative er-ror of each parameter is between 2% and 5%, indicating that the operating conditions constructed by the improved K-mean clustering algorithm combined with the principal component analysis method have high precision, and have a strong representation of the vehicle operating conditions.

1. 引言

城市化和机动化的进程使机动车保有量不断增加，机动车排放对环境造成的污染问题日益严重 [1] 。机动车排放标准认证与车辆运行工况有十分重要的联系，车辆行驶工况表示某种车型在某种交通环境下运行时的速度–时间曲线，对新车型的技术开发和评估也有重要意义 [2] [3] 。

为了构建更为精准的运行工况，国内外学者进行大量研究。路尧等 [4] 调研国内多个代表性城市的实际运行工况，获得车辆实际道路运行数据，利用短行程法构建轻型汽车运行工况。Wang等针对中国城市特点构建运行工况，并将其与欧洲运行工况和美国运行工况进行比较，然后对不同国家运行工况下的排放因子进行对比分析。彭育辉等 [5] 利用K-均值聚类方法对车辆行驶数据进行分析，再用Silhouette函数对聚类结果进行筛选，增加了人为选择的准确度，然后根据聚类结果进行车辆运行工况的构建。曹骞等 [6] 用自主驾驶的方法采集车辆的行驶数据，然后用马尔科夫链算法进行行驶工况的构建，最后针对沈阳市乘用车构建出具有代表性的运行工况。郭家琛等 [7] 用自编构建码器对数据进行降维处理，在聚类后用Silhouette函数对聚类结果进行筛选，构建车辆运行工况。段宇帅等 [8] 用传统的K-均值聚类算法和主成分分析法进行运行工况的构建。周溪召等 [9] 同样通过传统的K-均值聚类算法对大连市汽车运行工况进行构建。上述研究在聚类时大多运用了传统的K-均值聚类算法，在聚类结果方面存在一定的不足，比如聚类结果不稳定，聚类结果容易陷入局部最优等问题。

为此，本文通过改进K-均值聚类算法，解决聚类时聚类结果不稳定和容易陷入局部最优的问题，并将改进的K-均值聚类算法结合主成分分析法应用于车辆运行工况的构建。并验证所构建工况的准确性与代表性。

2. 车辆运行数据采集

为了使采集的车辆运行数据能更加有效的代表当地的实际道路交通状况，使构建的运行工况更具代表性。本研究将远程监控终端设备和北斗车载定位终端设备与试验车辆内的终端接口相连接，在不干扰试验车辆原本行驶计划的情况下，让试验车辆在实际道路进行同往常一样的行驶，然后利用车载终端所具有的发动机信息解析和存储功能、卫星定位功能采集试验车辆实际道路运行状况下的车速信息和定位信息，并利用车载终端所具有的远程通讯功能将所采集到的信息传送到远程监控数据平台，然后通过客户端登录获得试验数据，将得到的试验数据用于后续的工况构建中。数据采集装置如图1。

Figure 1. Data acquisition equipment

图1. 数据采集装置图

3. 主成分分析和改进的K-均值聚类算法

3.1. 主成分分析法

主成分分析法是把原数据中的多个变量进行处理，重新组合成新的综合变量，这些新的综合变量被称为主成分 [10] 。主成分能够反映原有变量的特征，并且主成分的数目相较于原来变量数目有所减少，达到数据降维的目的。经过主成分分析之后得到的主成分比原来的变量更加简洁且具有更高的独立性，为后续数据分析带来便利。

主成分分析的具体计算步骤如下：

1) 对原始数据进行向量化和标准化

采集m个样本，并且每个样本里包含n个变量，然后将其构造成一个样本矩阵，样本矩阵如式1：

$x=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& \cdots & x_{1n}\\ x_{21}& x_{22}& x_{23}& \cdots & x_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{m1}& x_{m2}& x_{m3}& \cdots & x_{mn}\end{array}\right]$ (1)

矩阵中 $x_{mn}$ 表示第m个样本的第n个变量。

由于特征参数量纲的不同，导致各变量的取值较为分散，进而导致后续数据分析的稳定性降低。所以为了避免上述情况的发生，对数据进行标准化处理。具体计算公式如式(2~4)：

${\bar{x}}_j=\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}}}{n}$ (2)

$s_j=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_{ij}-{\bar{x}}_j\right)}^2}}{n-1}}$ (3)

$Z_{ij}=\frac{x_{ij}-{\bar{x}}_j}{s_j}$ (4)

式中i为 $1,2,3,\cdots ,m$ ；j为 $1,2,3,\cdots ,n$ ；

进行标准化后的样本矩阵为

$Z=\left[\begin{array}{ccccc}{Z}_{11}& Z_{12}& Z_{13}& \cdots & Z_{1n}\\ Z_{21}& Z_{22}& Z_{23}& \cdots & Z_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ Z_{m1}& Z_{m2}& Z_{m3}& \cdots & Z_{mn}\end{array}\right]$

矩阵中 $Z_{mn}$ 表示标准化之后的第m个样本的第n个变量。

2) 计算 $Z$ 相关系数矩阵，具体计算公式如式5：

$R=Z^{\text{T}}\cdot Z$ (5)

$R=\left[\begin{array}{ccccc}{r}_{11}& r_{12}& r_{13}& \cdots & r_{1n}\\ r_{21}& r_{22}& r_{23}& \cdots & r_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& r_{n3}& \cdots & r_n{}_n\end{array}\right]$

矩阵中 $r_n{}_n$ 表示变量之间的相关系数，其中下标相同的相关系数为1。

3) 算矩阵的特征值及特征向量

对相关系数矩阵进行计算，根据特征方程 $\left|\lambda I-R\right|=0$ ，计算出特征值，然后将特征值从大到小按顺序排列 ${\lambda }_1\ge {\lambda }_2\ge {\lambda }_3\ge {\lambda }_4\cdots \ge {\lambda }_n\ge 0$ ；然后计算出每个特征值 ${\lambda }_i$ 对应的特征向量 ${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,\cdots ,{\alpha }_n$ 。

4) 计算各主成分贡献率和累计贡献率

根据上面的计算结果，计算主成分的贡献率，贡献率的大小代表对原信息综合反映能力，贡献率值越大代表性越强。具体计算公式如式(6~7)：

${\delta }_i=\frac{{\lambda }_i}{{\displaystyle {\sum }_{k=1}^n{\lambda }_k}}\left(i=1,2,3,\cdots ,n\right)$ (6)

${\zeta }_i=\frac{{\displaystyle {\sum }_{k=1}^i{\lambda }_k}}{{\displaystyle {\sum }_{k=1}^n{\lambda }_k}}\left(i=1,2,3\dots n\right)$ (7)

经过计算后，通常认为累计贡献率大于80%时，主成分具有较好的代表性，可以较为准确的反映原数据特征。

3.2. 改进的K-均值聚类算法

K-均值聚类作为一种迭代聚类算法，其相似程度用距离来衡量，把需要进行分类的数据按照分类标准划分成k类，通过计算每类所有点的均值确定聚类中心，用聚类中心来表示每个类 [11] 。K-均值聚类算法相较于其他聚类算法更加适用于数据量较大的时候。但其也存在一定的缺点，比如聚类结果的稳定性不好、聚类时容易陷入局部最优等。所以为了解决这些问题，对K-均值聚类算法进行改进，具体步骤如下：

步骤一：对每个样本进行计算，求其均值当作每个类的聚类中心，计算公式如式8：

$z_1=\frac{{\displaystyle {\sum }_{i=1}^n{f}_i}}{n}$ (8)

步骤二：令k = k + 1(k初始值为1)，当满足k > K时，终止聚类。

步骤三：定义新参数 $l_m$ ，对每个点的参数 $l_m$ 进行计算，当 $l_m$ 最大时，选其对应的点作为下一类的初始聚类中心。 $l_m$ 计算公式如式9：

$l_m={\displaystyle {\sum }_{i=1}^n\max \left(d_{k-1}^i-\Vert f_m-f_i\Vert ,0\right)}$ (9)

式中 $d_{k-1}^i$ 表示 $f_i$ 和它所在类中心的欧氏距离。

步骤四：本研究中 $f_i$ 和聚类中心的距离用欧式距离来表示，寻找与 $f_i$ 最近的中心点，将其划分到此类。

步骤五：对各新类的中心点重新进行计算， $z_{ji}=\frac{{\displaystyle {\sum }_{i=1}^n{f}_{ji}}}{N}$ ，N代表第i类中数据的数量。然后计算准则函数F值，计算公式如式10：

$F={\displaystyle {\sum }_{j=1}^k{\displaystyle {\sum }_{i=1}^n{\Vert f_{ji}-z_i\Vert }^2}}$ (10)

步骤六：判断准则函数值F是否收敛，若收敛，进行步骤二，若不收敛进行步骤四，在新类中心基础上进行进一步迭代。

4. 运行工况构建

4.1. 运动学片段划分

车辆在实际道路运行时，会受到道路交通环境的影响，导致运行过程必然经历很多次的起步和停车。所以从运动学角度出发，将车辆的一次启停用运动学片段来描述 [12] 。将一个怠速开始点到下一个怠速开始点定义为一个运动学片段，运动学片段划分示意如图2。

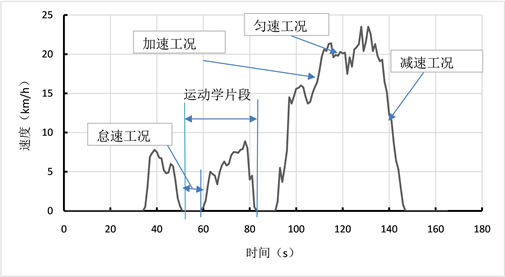
Figure 2. Schematic diagram of kinematic segment division

图2. 运动学片段划分示意图

划分运动学片段是为了更好的分析每个运动学片段的特征，每个运动学片段包含怠速、加速、减速和匀速四种状态，并且每种运动状态有着不同的定义方式，具体定义方式如下：

1) 怠速状态：车速为0并且发动机处于工作状态的车辆运行状态。

2) 加速状态：车速不为0并且车辆加速度大于等于0.15 m/s²的车辆运行状态。

3) 减速状态：车速不为0并且车辆加速度小于等于−0.15 m/s²的车辆运行状态。

4) 匀速状态：车速不为0并且加速度的绝对值小于等于0.15 m/s²的车辆运行状态。

在完成运动学状态划分后，利用Matlab编写相应的程序进行运动学片段的划分，最终将试验数据划分得到5250个运动学片段。完成运动学片段的划分后，由于部分运动学片段并不适用于工况构建，因为部分运动学片段受到突发状况的影响，导致这些运动学片段不符合车辆正常运行情况，所以要对运动学片段进行筛选。筛选条件如表1。

Table 1. Kinematic segment screening conditions

表1. 运动学片段筛选条件

如表1所示，对运动学片段时间进行限制，要求运动学片段时间大于10秒；加速度绝对值小于等于5 m/s²；速度范围在5 km/h到100 km/h之间；加速度为0的时间不超过10秒；按照此筛选条件进行运动学片段的筛选，使得到的运动学片段更具代表性。在对原来的5250个运动学片段进行筛选后得到4526个运动学片段。

4.2. 特征参数选取与计算

运动学片段特征仅用速度和时间来描述不够全面，所以为了更加具体的描述运动学片段特征，需要定义一些特征参数，然后用这些特征参数定量的描述运动学片段特征。描述性特征参数如表2，统计性特征参数如表3。

Table 2. Descriptive feature parameter

表2. 描述性特征参数

Table 3. Statistical characteristic parameters

表3. 统计性特征参数

对本研究中划分的运动学片段进行特征参数计算。得到计算结果如表4。

Table 4. Kinematic segment characteristic parameter calculation results

表4. 运动学片段特征参数计算结果

4.3. 主成分分析结果

根据计算得到主成分贡献率和累计贡献率如表5，由表可以看出主成分1的贡献率最高，达到41.17%，说明其对原始数据的解释度最大；紧随其后的是主成分2，其贡献率为19.17，累计贡献率为60.34%；主成分3的贡献率为14.16%，累计贡献率为74.50%；主成分4的贡献率为9.09%，累计贡献率为83.59%；所以前4个主成分的累计贡献率高于80%，说明前四个主成分能比较全面的反映原数据特征，即将运动学片段的14个特征参数降维为4个主成分 [13] 。

Table 5. Principal component contribution rate and cumulative contribution rate

表5. 主成分贡献率和累计贡献率

对主成分与特征参数的相关性进行计算，得到主成分与特征参数相关性如表6，由表6可以得出主成分1主要代表的是加速时间、运动片段时间、减速时间、平均速度、匀速时间、平均运行速度、最大速度；主成分2主要代表的是平均减速度、平均加速度、最大减速度、最大加速度；主成分3主要代表的是平均速度；主成分4主要代表的是怠速时间。

Table 6. Principal components are correlated with characteristic parameters

表6. 主成分与特征参数相关性

对主成分得分矩阵进行计算，结果如表7。将其用于后续聚类分析。

Table 7. Principal component score matrix

表7. 主成分得分矩阵

4.4. 改进的K-均值聚类结果分析

运用改进的K-均值聚类算法对运动学片段进行聚类，将运动学片段分成三类，聚类后各类平均特征值如表8。由表8可以看出，第1类运动学片段的平均速度最高，怠速比例最低，代表郊区或者环城高架桥高速路况；第2类运动学片段平均速度和怠速比例均处于其他两类之间，代表城市道路通畅时行驶情况；第3类平均速度最低，怠速比例最高，代表城市道路拥堵时行驶情况。

Table 8. The average eigenvalue after clustering

表8. 聚类后各类平均特征值

4.5. 运行工况合成

根据中国汽车行驶工况构建标准以及车辆实际运行情况，将本研究构建的运行工况的持续时间定为1800 s，这样能更好的反映车辆的实际道路运行情况，同时也满足将其用于排放测试时的标准。

$P_n=\frac{T_n}{T_z}\times 100\text{\%}$ (11)

式中 $P_n$ 表示第n类运动学片段时间占总运动学片段时间的比例， $T_n$ 为第n类运动学片段总时间， $T_z$ 是总运动学片段时间。

通过式11计算得到郊区或者环城高架桥高速路况所占的比例为15.4%，城市道路通畅时运行状态所占比例为57.8%，城市道路拥堵时运行状态所占比例为26.8%。根据各类运行状态所占比例，在第1类、第2类和第3类运动学片段库选取运动学片段用于工况构建。选取运动学片段时，通常选取聚类后与本类的特征值有最大相关性的运动学片段作为代表片段，而在本研究中，依次选取相关系数较大的运动学片段组成运动学片段库，然后用于后续的运行工况合成。

按上述方法，本研究在第1类运动学片段中选择107号片段、125号片段、212号片段组成第1类运动学片段库；在第2类运动学片段中选择525号片段、561号片段、623号片段、651号片段、1662号片段、1671号片段、1783号片段、2485号片段、898号片段、995号片段组成第2类运动学片段库；在第3类运动学片段中选择3521号片段、3631号片段、3789号片段、3965号片段、4021号片段、4156号片段、4258号片段、4321号片段组成第3类运动学片段库。根据各类运动学片段在构建工况时所占的时间比例，分别选取运动学片段来构建工况。按上面所求比例在第3类运动学片段库中选1个运动学片段；在第2类运动学片段库中选5个运动学片段；在第1类运动学片段库中选4个运动学片段；将选出的运动学片段构建成运行工况曲线如图3。

Figure 3. Vehicle driving cycle

图3. 车辆运行工况

4.6. 工况验证

通过比较构建的车辆运行工况的特征参数值和总样本数据的特征参数值，判断构建的运行工况是否能准确的反映车辆实际道路运行状况。选取的特征参数有平均速度 $V_m$ 、怠速比例 $P_d$ 、减速比例 $P_j$ 、加速比例 $P_s$ 、平均加速度 $a_m$ 、平均加速度 $a_n$ 。将这6个特征参数作为判定标准，把本研究构建的运行工况的特征参数值和总样本数据的特征参数值进行对比分析，结果如表9。

Table 9. Comparison of character parameter values

表9. 特征参数值对比

由表9可得，自主构建的运行工况和总样本数据的平均速度相对误差为2.0%，怠速比例相对误差为2.5%，减速比例相对误差为2.2%，加速比例相对误差为2.3%，平均加速度相对误差为2.2%，平均减速度相对误差为4.8%。由此可见本研究构建的运行工况和总体数据的特征参数值相对误差很小，可以较好地反映车辆实际道路运行情况。

5. 结论

1) 对数据预处理后进行运动学片段的划分与筛选得到4526个运动学片段，用主成分分析法将数据降维成4个主成分，再用改进的K-均值聚类算法聚类为3类，最后选取每类的代表片段构建车辆运行工况。

2) 与传统的K-均值聚类算法构建的运行工况相比，用改进的K-均值聚类算法构建的运行工况精度更高。用改进的K-均值聚类算法构建的运行工况和总样本数据的平均速度相对误差为2.0%，怠速比例相对误差为2.5%，减速比例相对误差为2.2%，加速比例相对误差为2.3%，平均加速度相对误差为2.2%，平均减速度相对误差为4.8%。说明该工况能很好的反映当地的车辆实际道路交通状况，该工况具有很高的可信度。

3) 构建的工况中郊区或者环城高架桥高速路况所占的比例为15.4%，城市道路通畅时运行状态所占比例为57.8%，城市道路拥堵时运行状态所占比例为26.8%，运行工况的路况构成存在一定的地域差异，本工况的构建为后续其他城市工况构建时的地域加权提供数据依据。