复杂网络能控性的研究进展

Recent Progress in Controllability of Complex Networks

摘要: 复杂网络是近年来新兴的热门跨学科科学，复杂网络的控制是当前复杂网络研究的焦点，也是复杂网络分析和研究的目标之一。综述了复杂网络能控性的最新研究成果，详细讨论了能控性理论、能控性优化方法和能控性鲁棒性。最后，本文发现复杂网络子网间结构对能控性的影响，遭受攻击后能控性可恢复理论以及多重网络能控性鲁棒性等方面的问题值得深入探索和研究。

Abstract: Complex networks are an emerging and popular interdisciplinary science in recent years. The con-trol of complex networks is the focus of current research on complex networks and is one of the goals of complex network analysis and research. The latest research results of complex network controllability are reviewed, and the controllability theory, controllability optimization method and controllability robustness are discussed in detail. Finally, it is found that the influence of complex network subnet structure on controllability, the theory of controllability recovery after attacks and the robustness of multiple networks controllability are worthy of further exploration and research.

1. 引言

21世纪以来，随着信息技术、网络化、智能化的发展，人类社会已经进入网络时代。互联网，交通网络，社会网络等均可以被抽象为复杂的网络。简单地说，如果把某个体看作是一个点，那么复杂网络就是连接这些点和线的复杂结构。早期复杂网络的研究发展过程如表1所示。此后，掀起了研究复杂网络的热潮。

Table 1. The development of complex network research

表1. 复杂网络研究发展历程

现今，复杂网络研究的主要方向大概为：复杂网络的能控性，复杂网络拓扑结构性质，复杂网络的结构稳定性等。这些研究方向提供了研究复杂网络的全新视角和方法。然而，复杂网络的控制是分析复杂网络的终极目标之一，而解决能控性问题的关键是找到网络中需要被控制的节点。2011年，Liu等人 [3] 研究了线性定常系统的结构能控性问题，建立了复杂网络能控性分析架构，引起了人们对复杂网络能控性前所未有的关注。此后，许多关于网络能控性的研究成果被发表在国际顶级期刊上。

鉴于网络能控性研究的蓬勃发展和一些突破性成果，本文对目前复杂网络能控性的研究工作进行了总结，旨在为国内相关研究者了解复杂网络能控性提供一个窗口。本文重点介绍了以下几个方面：第一部分主要介绍网络能控性的理论基础。第二部分主要讨论网络能控性优化难题。第三部分重点介绍了网络能控的鲁棒性研究成果。最后，对本文进行了归纳和展望。

2. 网络能控性理论框架

在网络理论中，如果有向网络中节点N₂到节点N₁之间存在一条有向路径，则有向网络中的节点N₁可被另一个节点N₂控制，能控性在经典控制理论中被用来描述动态系统的控制行为。2007年，Lombardi等人 [4] 首先将经典控制理论应用于复杂网络的能控性分析，并将网络能控性问题抽象为线性系统。

从结构上讲，非线性系统的能控性问题同线性化系统的能控性类似。因此，为了研究复杂系统中的非线性动态行为，不妨先考虑如下的线性定常系统的状态方程：

$\stackrel{\dot{}}{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)$ (1)

其中， $x\left(t\right)={\left(x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right)\right)}^{\text{T}}$ 表示该系统的n维状态变量， $A\in R^{n\times n}$ 是系统矩阵， $u\left(t\right)={\left(u_1\left(t\right),u_2\left(t\right),\cdots ,u_m\left(t\right)\right)}^{\text{T}}$ 表示该系统的m维外部输入变量， $B\in R^{n\times n}$ 是输入矩阵。当且仅当能控性矩阵满足：

$rank\left(B,AB,\cdots ,A^{N-1}B\right)=N$ (2)

则系统(1)完全能控。此充要条件称为Kalman能控性判据 [5] ，继而网络能控性问题转化为能控性矩阵的秩的计算问题。

但是，由于该判据需要不断地计算矩阵的秩，且还需明确网络拓扑中的所有权重，而在实际情况中，复杂网络拓扑的权重不可测或不确定，故该判据无法直接引申到复杂网络中。对此，Liu等人 [3] 引入线性系统结构能控性理论及图的匹配学说，将系统的结构能控性问题转化为图匹配问题，一定程度上降低了时间的复杂度。

结构能控性基本定理将结构能控性问题转化为择取驱动节点的问题，而后将外部输入信号施加到驱动节点，以确保所产生的系统 $\left(A,B\right)$ 结构可控，对此Liu等人给出最小输入定理：

定理1 [3]

$N_I=N_D=\max \left\{N-\left|M^{*}\right|,1\right\}$ (3)

其中N_D，N_I表示控制网络所需的最小驱动节点数， $\left|M^{*}\right|$ 为有向网络最大匹配的节点数。

利用结构能控性理论架构求解最小驱动节点流程步骤，如图1所示。

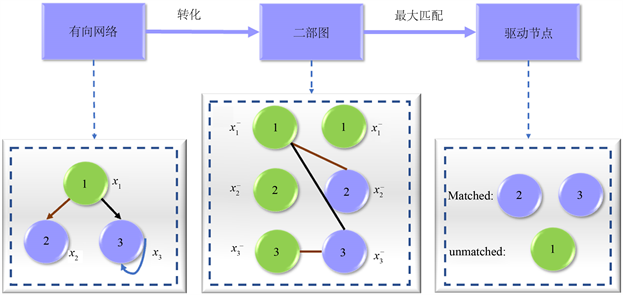
Figure 1. The flow chart of minimum drive node is solved by structural controllability theory

图1. 结构能控性理论求解最小驱动节点流程图

由于Liu等人 [3] 提出的结构能控性分析框架偏向有向网络，忽略了无向网络和部分边权值已知网络的不适用问题。因此，Yuan等人 [6] 提出了一个适用于任何网络的基于PBH准则 [7] 的严格能控性理论，证明了控制网络所需的动力源节点的最小数目等于网络相应矩阵特征值的最大几何重数。

定义1 [8] 系统(1)实现能控所需最小驱动节点的数量为，满足PBH判据时所有矩阵 $B$ 的秩最小值，即

$N_D=\min \left\{rank\left(B\right)\right\}$ (4)

接着，得到控制网络所需的最小输入定理：

定理2 [6] 线性定常系统(1)实现完全能控所需最小驱动节点数N_D等于矩阵A的最大几何重数，即

$N_D=\underset{i}{\max }\left\{\mu \left({\lambda }_i\right)\right\}$ (5)

由于定理2只使用矩阵的特征值和秩，对网络的边权重并未有要求，故定理适于任意网络。

Yuan等人 [6] 求解出N_D后，又给出了找具体驱动节点的方式。由定理2，控制网络所需的驱动节点个数为：

$N_D=\underset{i}{\max }\left\{\mu \left({\lambda }_i\right)\right\}=\underset{i}{\max }\left\{N-rank\left(A-{\lambda }_i{I}_N\right)\right\}$ (6)

记使式(6)取得最大值的特征值为 ${\lambda }^M$ ，则

$N_D=\mu \left({\lambda }^M\right)=N-rank\left(A-{\lambda }^M{I}_N\right)$ (7)

所需的驱动节点为矩阵 $A-{\lambda }^M{I}_N$ 线性相关行所对应的节点。综上，采用严格能控性理论寻驱动节点流程图如图2所示。

Figure 2. Flow chart of minimum drive node set solved by strict controllability theoretical framework

图2. 严格能控性理论框架求解最小驱动节点集流程图

严格能控性学说虽适用度广，但时间复杂度高。结构能控性理论和严格能控性理论虽为研究复杂网络能控性提供了理论架构，但都忽略运行真实网络时的能量消耗问题。Sun [9] 基于Gramian矩阵的奇异性提出网络能控性的理论研究框架。能量最优控制中，系统的输入和对应的运动路径如下所示：

$\begin{array}{l}u\left(t\right)=B^{\text{T}}{\varphi }^{\text{T}}\left(t_0,t\right)W^{-1}\left(t_0,t\right)\left[\varphi \left(t_0,t_1\right)x^{\left(1\right)}-x^{\left(0\right)}\right],\\ x\left(t\right)=\varphi \left(t,t_0\right)\left[x^{\left(0\right)}+M_{t_0,t_1,t}\left(\varphi \left(t_0,t_1\right)x^{\left(1\right)}-x^{\left(0\right)}\right)\right]\end{array}$ (8)

其中 $M_{t_0,t_1,t}=W\left(t_0,t\right)W^{-1}\left(t_0,t_1\right)$ ， $W\left(t_0,t_1\right)={\displaystyle {\int }_{t_0}^{t_1}\varphi \left(t_0,t\right)B{B}^{\text{T}}{\varphi }^{\text{T}}\left(t_0,t\right)\text{d}t}$ ， $\varphi \left(t_0,t_1\right)={\text{e}}^{\left(t_0-t_1\right)A}$ ， $W\left(t_0,t_1\right)$ 即为Gramian矩阵。

通过最少的输入来控制线性系统通常具有过高的能量需求，为显着降低控制能量，Alizadehs等人 [10] 研究了识别最小输入节点集的问题，将其映射到寻找联合最大匹配和最小支配集，以便在限制最长控制链长度的同时确保能控性。

3. 网络能控性优化

能控性优化即减少最小驱动节点集合中的数量。现有，能控性优化方法：改变网络的拓扑结构和边指向。

Wang等 [11] 提出了添加边的途径来控制整个网络。具体方法如图3所示。图3(a)网络(30个节点图)，图3(b)中的所有匹配路径按顺序连接(网络最大匹配集中孤立点和简单有向路径依次连接的新回路)，从节点10开始并在节点29结束，其中红色边是借助算法添加的边，绿色为匹配边以，灰色为未匹配边。

(a) (b)

Figure 3. Perturbation algorithm diagram for complex networks, cited in [11]

图3. 复杂网络微扰算法图，引自文献 [11]

Wang等人 [11] 的方式要求提升网络中边的数量，Hou等人 [12] 则建议利用重连冗余边的途径升级网络的能控性。此法虽强化了网络能控性，但在真实网络中，转变拓扑结构难度较大，成本过高。

因此，Hou等人 [13] 在不改变网络拓扑构造的基础上，提出了基于网络的节点剩余度对边指向改变进而提高能控性的方法，数值结果表明，该方法的优化效果明显优于随机边缘取向的方法。由于此法是一种启发式算法，进行边指向，当选择满足条件的节点时具有随机性，故不会使网络能控性最优，于是，Xiao等人 [14] 构造了一个交换网络成功将最优能控性的边指向问题转化为解交换网络节点的最大独立集问题。先建立任意网络的有向对称图，再根据连边规则构造交换网络，最后求出交换网络的最大独立集；如图4所示。

Hou等人 [15] 指出，上述使用交换网络寻找网络中最大的独立集的问题对于大规模网络来说是NP难问题，在计算上也是不可行的。因此，反转网络中边指向来优化网络能控性。

然而在真实的网络中，如城市交通网络，存在控制节点和状态节点。不过，前面提到的网络能控性优化主要针对只包含状态节点而没有控制节点的网络。故而，Li等人 [16] 对任意网络能控性优化难题进行研究。用遗传算法来生成最优网络拓扑，实现PBH判据下的完全能控。

另外，Li [17] 基于保度边缘交叉连接的优化算法，用于复杂网络结构的能控性，分析了如欧洲航空网络等真实网络结构的抗击优化效果。Zhang [18] 提出采用反转边指向来更改网络控制模式的优化算法。在集中模式下，驱动节点的数量大大降低，网络更易控制。

4. 网络能控性鲁棒性

复杂网络的能控性鲁棒性指在受到袭击时，复杂网络维持能控性的综合能力 [19] 。其中基于能控性曲线的定义为能控性鲁棒性即系统在遭受节点或连边攻击之后，余下网络的能控性。其中节点攻击下能控性鲁棒性定义如下：

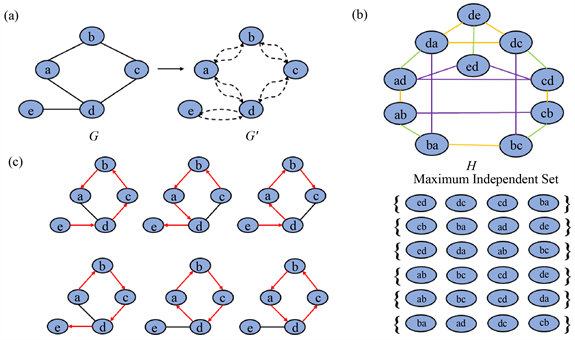
Figure 4. Solving the flow chart of the maximum independent set of switching network nodes. (a) Simple 5-point 5-sided undirected network G and its directed symmetric network G'; (b) According to the constructed switching network; (c) The maximum independent set corresponds to the direction set that generates the least number of driver nodes

图4. 求解交换网络节点的最大独立集流程图。(a) 简单5点5边无向网络G，及其有向对称网络G'；(b) 根据G构建的交换网络H；(c) 最大独立集对应于产生最少数量的驱动节点方向集

$n_D^N\left(i\right)\equiv \frac{N_D\left(i\right)}{N-i},i=0,1,\cdots ,N-1$ (9)

其中 $N_D\left(i\right)$ 是当i个节点被攻击后，所需的控制节点数； $N-i$ 为i个节点被攻击后的网络剩余节点数。式(9)定义了攻击情况下能控性变化的动态过程。继而由平均得到整体的能控性鲁棒性，如式 (10)所示：

$R_c^N=\frac{1}{N}{\displaystyle \underset{i=0}{\overset{N-1}{\sum }}{n}_D^N\left(i\right)}$ (10)

同理，连边攻击下能控性鲁棒性定义如下：

$n_D^E\left(i\right)\equiv \frac{N_D\left(i\right)}{N},i=0,1,\cdots ,M$ (11)

其中N和M分别表示网络节点和连边数。整体的能控性鲁棒性为：

$R_c^E=\frac{1}{M+1}{\displaystyle \underset{i=0}{\overset{M}{\sum }}{n}_D^E\left(i\right)}$ (12)

综上， $R_c^N$ 或 $R_c^E$ 的值越小，在节点或连边攻击的情况下，整体的能控鲁棒性越好。

近年来，对复杂网络的攻击成为研究热点之一，不同的攻击策略有不同的特点和效果。针对随机攻击，Sun等人 [20] 指出，在随机攻击下，网络所需的控制节点数增量由网络中关键连边的数量估算得到：

$\Delta N_D=\frac{M_r\cdot M_c}{M},\text{if}{M}_r\le M_c$ (13)

当被攻击的连边数小于关键连边数时，关键连边会以 $p\left(M_c\right)=\frac{M_c}{M}$ 的概率被攻击。每攻击一条关键

连边，所需的控制节点数增加1；若攻击到非关键连边，所需控制节点数保持不变。但实际上，攻击1条连边就可能引起关键连边的变化，如图5所示，当连边(2, 3)和(3, 4)被攻击以后，非关键连边(2, 4)变成了关键连边。

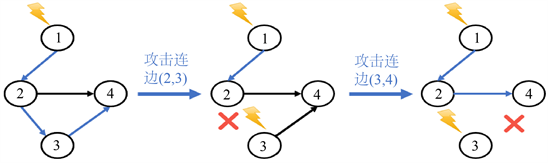
Figure 5. Changes in the course of the attack on the critical edge

图5. 关键连边遭受攻击过程的变化

针对蓄意攻击，Sun等人 [20] 提出了基于关键连边的攻击策略。Lou等 [21] 在Sun等人 [20] 的基础上，提出了层级连边攻击，虽然该方法计算复杂度较高，但是攻击效果较好。对于启发式攻击，Li等人 [22] 通过邻域信息来提高随机算法搜索关键节点集合的能力，攻击效率显著提高。

能控性鲁棒性优化改善旨在增强复杂网络防御各种攻击的能力 [23] 。Wang等人研究网络遭受蓄意攻击时如何拥有较高的能控性。提出了控制鲁棒性指数：

$CR=\frac{1}{N}{\displaystyle \underset{q=1/N}{\overset{1}{\sum }}\frac{s\left(q\right)}{N_D\left(q\right)}}$ (14)

其中N是节点数， $s\left(q\right)$ 表示消除 $q\times N$ 个节点后，网络最大弱连通子图中的节点比例， $N_D\left(q\right)$ 表示移除 $q\times N$ 个节点后网络需要的驱动节点的最小数。因此，提出了一种通过交换随机边来增强CR的方式，尽管复杂度太高。

传统上，CR是通过攻击模拟确定的，这在计算上很耗时，甚至不可行。Lou等 [24] 使用卷积神经网络(CNN)开发了改进的CR预测方法。与传统方式相比，提出的基于CNN的预测因子提供了更好的预测测量。

5. 总结与展望

近年来，随着复杂网络科学的发展，学界从不同层面对复杂网络的能控性进行了深入研究，取得的成果斐然。除了以上几个方面，关于网络能控性还有很多其他的研究，比如复杂网络的子网间的结构对能控性的影响 [25] 。

针对以上三个问题，未来可研究内容包括：

1) 当前理论研究成果主要包括结构能控性和严格能控性，但对网络能控性的结构特征缺乏定量叙述和完善认识 [26] ，且现有理论观点仅适用于理想网络，而实际的复杂网络大多为非线性系统，故而，如何将相关理论与实际问题结合来研究复杂系统是今后集中持续研究的方向 [3] 。

2) 在如何优化网络能控性的问题上，目前的能控性优化方法主要是改变网络拓扑结构和改变边指向，但在现实生活中很难改变。因此，在不改变网络拓扑构造和边指向的前提下，优化网络的能控性是未来一段时间的研究重点 [9] 。

3) 现实中的复杂网络系统难免会遭遇天灾人祸，这将增加网络控制的困难程度。对相关多重网络能控性鲁棒的全面研究远未得到有效的重视，能否以较低的网络代价提高网络的能控性鲁棒性是将来研究的重要方向 [23] 。

基金项目

唐山市科学技术研究与发展计划(第七批)项目(19130222g)；教育部协同育人项目(202102088007)。