基于DFT的氮参杂TiO₂ (101)检测H2S的气敏特性研究

Study on Gas Sensing Characteristics of Nitrogen Doped TiO₂ (101) for Detecting H2S Based on DFT

摘要: SF₆绝缘气体作为电力系统中最重要的气体绝缘介质之一，具有灭弧能力强、无毒等突出优点。但其在设备内部绝缘缺陷产生的局部放电作用下，会分解生成包括SO₂F₂，SO₂和H₂S在内的几种特征物质，降低SF₆气体绝缘性能。而通过化学气体传感器检测SF₆特征分解组分，实现气体绝缘设备故障诊断与在线监测技术，已被认为是估算电气工程中绝缘设备运行状态的可行方法。研究发现TiO₂纳米管传感器对SF₆分解组分H₂S具有良好的响应，因此TiO₂纳米管传感器具有增强的敏感性和对气体分子的响应。本文基于密度泛函理论方法模拟了SF₆分解组分H₂S在N掺杂TiO₂上的吸附特性。结果表明，N-TiO₂对H₂S的敏感性较好，吸附后电导率发生明显变化。

Abstract: As one of the most important gas insulation media in power system, SF₆ insulating gas has the outstanding advantages of strong arc extinguishing ability and non-toxic. Under the action of partial discharge caused by the internal insulation defects of the equipment, several characteristic substances, including SO₂F₂, SO₂ and H₂S, will be decomposed and generated, which will reduce the insulation performance of SF₆ gas. By detecting SF₆ characteristic decomposition components by chemical gas sensor, fault diagnosis and on-line monitoring technology of gas insulation equipment has been considered as a feasible method to estimate the running state of insulation equipment in electrical engineering. The study found that N-TiO₂ sensor has a good response to the H₂S of SF₆ decomposition components, so N-TiO₂ sensor has enhanced sensitivity and response to gas molecules. The adsorption characteristics of SF₆ decomposition component H₂S on N doping TiO₂ are simulated based on density functional theory method. The results show that the sensitivity of the N-TiO₂ to the H₂S is good, and the conductivity changes obviously after adsorption.

1. 引言

在变电绝缘工程中长期存在的SF₆在绝缘设备中，难免的缺陷会导致SF₆分解。然后，SF₆的副产物将在氧气和微量水的存在下反应 [1] ，形成包括SO₂F₂，SO₂和H₂S在内的几种物质。已经证明，这些杂质的存在会降低SF₆的绝缘性能，并可能导致电力系统瘫痪 [2] [3] [4] [5] 。因此，SF₆分解产物的在线检测一直是电气工程领域的研究热点 [6] ，用于估计绝缘系统的运行状态并防止高压系统中的相关绝缘缺陷 [7] 。

近年来，基于TIO₂的气体传感器因其快速响应和对目标分子的高灵敏度而受到了广泛的关注。电阻率型传感器的感应机制取决于吸附剂表面与气体分子之间的电荷转移，从而导致电导率变化得以检测 [8] [9] 。

据报道，在众多元素中，对分子相互作用具有高催化活性的N是TIO₂的掺杂剂，以实现其在某些小气体检测中的应用。为了进一步探索其应用，本文基于密度泛函理论方法模拟了N掺杂的TIO₂在三种SF₆分解产物H₂S上的吸附行为。还介绍了前沿分子轨道理论以了解吸附过程中电导率的变化。结果表明N-TIO₂表面位置H₂S的性能相当好，表明其强大的潜力正被准备用作电气工程领域的实用传感器。

用SF₆气体来进行的绝缘电气设备在广泛的电气行业中有不可估计的前途和价值。SF₆气体因为自己的特别的性质，所以有极其良好电气绝缘强度，是均匀电场中空气的电气绝缘强度的2.5倍左右。而SF₆的灭弧能力约为空气的100倍，其冷却效果远强于空气 [10] ，与电气设备相比，传统的变压器电站具有占地面积小、不受外界天气影响、配置灵活、安全可靠等优点 [10] 。可以通过对气体绝缘设备某些局部放电的重要信息来对局部放电现象进行监视和数据处理，这样就可以发现早期不容易检测出的高压电气设备所存在的绝缘缺陷，避免了事故的发生，具有预见性和精确性等特点，所以加强对设备的重点监控，提前预警是非常重要的。纯净的SF₆气体没有气味、没有味道、没有毒性、不容易点燃，致其分解的温度也要大于500℃。但是，如果在电气绝缘的SF₆气体中混有极其少量的氧气和水蒸气的话，则SF₆气体就会进行分解，从而会引起氧气和水蒸气的复杂化学反应，如二氧化硫和硫化氢等，产生稳定的有毒性或腐蚀性气体成分，这样不仅SF₆气体的内部耐电强度会受到影响，而且还会加速绝缘设备老化。

CIGRE对于H₂S体积分数是有严格的规定的，其具体运行控制指标初步定为：H₂S体积分数 ≤ 0.5 μL/L [11] 。国家电网公司企标《SF₆气体分解产物检测技术现场应用导则》给出了GIS设备状态判断用分解产物参考指标 [11] 。因为局部放电所生成的特征产物浓度通常都比较低，所以要去摸索和了解GIS等SF₆气体在设备内由于不同因素而导致的分解情况，且这些分解的气体都是稀有气体，不容易被察觉，所以对于SF₆气体分解的重要特征组分的定量检测难度都比较高。检测管法、气相色谱法红外、紫外吸收光、谱法气体传感器法是目前实用也是实验和研究中的主要监测的办法。

2. 实验手段

2.1. 密度泛函理论

在MS (Materials Studio)软件中所建立的模型，使用进过Kohn-Sham的方式实现的密度泛函理论最常见的方法。在Kohn-Sham DFT的框架中，最难处理的多体问题(由于处在一个外部静电势中的电子相互作用而产生的)被简化成了一个没有相互作用的电子在有效势场中运动的问题 [12] 。电子间库仑相互作用的影响与原子外部的势场是被这个有效势能囊括的，比如，交换原子所需要的能量(交换能)和相关原子相互作用的能量(相关作用能)。虽然到目前为止求解交换相关能EXC的办法还没有被准确的定义出来，但使用局域密度近似(LDA近似)用近似求解方法来求解还是最方便容易的方法。

K-S方程是可以通过密度泛函理论中的薛定谔方程来改进和改善的，并且各自之间且无联系的自由电子动能也可以通过公式里面的动能来进行分析和计算。

2.2. 第一性原理

第一性原理以原子核与电子相互作用的原理为基础和原子核与电子基本运动定律为原则，通过使用量子力学中所包含的原理，最开始的出发点就是实际，然后经过某些相近似于这些实际的模拟处理，进而提出了的一些算法来求解薛定谔方程，并将这一过程直接的称为第一性基本原理。广义的第一性原理一般有Hartree-Fock自洽场计算为基础的从头算和密度泛函理论(DFT)计算两种。

以密度泛函理论为基础和在密度泛函理论基础上发展衍生出来的第一性原理电子结构计算方法有LDA和GGA两种方法，这两种方法对比以密度泛函理论为基础的老式传统方法，不但能给出描述系统微电子特性的物理量，如波函数、态密度等，还能得出电子间相互作用的各种至关重要的参数等优点。在此基础上，还能得到了相关能、电离能、比热、电导率、光电子能谱、穆斯堡尔谱等宏观物理性质参数，用密度泛函理论来计算的一些结果可以直接与实验进行比较。随着社会的发展，越来越多的应用程序的开发和商业软件的发布，使得基于密度泛函理论的第一种基本计算方法得到了广泛的应用。

原子的晶体结构、晶格参数、带宽结构、密度状态(DOS)、光学性质、磁性和全能量可以通过密度泛函理论来进行实验计算和估计预期。

2.3. 仿真内容及方法

基于SF₆局部放电分解特性的SF₆气体绝缘设备故障诊断法具有灵敏度高、不受外界干扰等优点，是保障智能电网安全稳定运行的可行在线监测法。基于第一性原理，利用Material Studios，探究SF₆局部放电特征分解气体组分之一H₂S分子，在N-TiO₂上的吸附特性(吸附距离、电荷转移量、态密度、前沿分子轨道等)，对研制相应的智能电网SF₆局部放电特征分解组分气敏传感器具有重要的工程和科学意义。

方法是利用Material Studios构建并优化H₂S分子及N-TiO₂的仿真模型，计算并分析单个及两个H₂S在N-TiO₂的表面吸附特性。然后对氮惨杂二氧化钛特征组分响应进行研究，得出表面特征和等离子改性参数。同时进行二氧化钛纳米管对硫化氢的响应特征实验。最后进行第一性原理仿真，对气敏特征进行解释。

本文是氮掺杂TiO₂晶面对硫化氢敏感响应过程通过仿真从微观仿真角度来进行计算，同时计算了各种情况的吸附能、电荷转移、稳定距离和态密度等，通过仿真的图像来体现气敏特性的特点参数，并基于这些数据来分析了吸附性能的好坏。

3. 仿真内容

到目前利用氮掺杂二氧化钛材料对SF₆分解成分中的H₂S检测的研究还相对较少。本文将研究锐钛矿型TiO₂ (101)对H₂S的气敏特性，通过Materials Studio软件计算出吸附所需要的能量(吸附能)电荷转移量、吸附距离以及态密度等的多个参数，利用这些参数来分析吸附特性。

3.1. 计算方法和参数设置

此仿真计算在Materials Studio软件的Visualizer模块建立模型，在Dmol³模块中完成计算和分析。在仿真最开始的时候，需要在Materials Studio软件中建立锐钛矿型二氧化硅(101)模型和H₂S分子的模型，搭建好模型后，调成棍球状显示，方便观看和测量，然后标出原子的距离和角度，具体图形如下图1所示。然后分别对所搭建好的二氧化硅(101)和H₂S分子的模型用Dmol³模块来进行计算优化。在优化完成后，接着根据文献找出最合适的位置，然后用氮原子取代二氧化硅(101)表面氧原子而后再进行优化以使微观模型的结构参数更加接近实际的理化标准。随后对二氧化硅(101)吸附H₂S结构进行优化，分别以硫原子、氢原子靠近方式进行两次次优化达到稳定吸附结构。最后，计算分析了表面吸附气体分子的稳定吸附体系的物理化学性质。

Figure 1. H₂S and TiO₂ (101) models

图1. H₂S和TiO₂ (101)模型

3.2. N-TiO₂模型建立及态密度分析

首先打开Materials Studio软件，然后找到已经构建好的未改性锐钛矿型TiO₂ (101)晶面的微观模型模型，然后打开Dmol³模块进行优化，在这个模块输入相关化了未改性锐钛矿型TiO₂ (101)晶面的微观模型的参数，等优化好了之后并研究了优化了未改性锐钛矿型TiO₂ (101)晶面的微观模型后，继续使用Dmol³模块，继续研究和查找文献找到氮最合适的惨杂位置，随后继续实验和仿真观测氮惨杂是否会对未改性TiO₂晶面基本性质产生影响，从而得出结论。最合适氮惨杂的TiO₂晶面的不同角度视图如图2(a)和图2(b)所示。

氮掺杂二氧化钛是在优化好的二氧化钛模型上进行原子取代，用一个氮原子取代二氧化钛表面的氧原子形成Ti-N键。

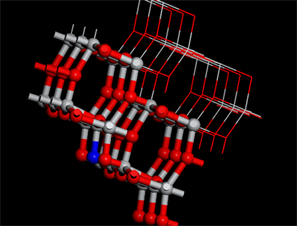
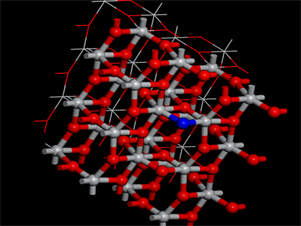(a) (b)

Figure 2. Nitrogen doped TiO₂ model

图2. 氮掺杂TiO₂模型

态密度是一种微观量，它表示的是单位能量范围内所能被允许的电子的数量，简而言之就是能说明在某种能量的区域内电子所分布的范围和情况。并且各种原子之间的互相的作用的状况和原子的化学键的重要信息以及各种轨道中的电子的分布的状况，这些都可以由态密度图来进行确切的反映。态密度图(DOS)有着非常大的作用，比如，能够根据费米能级是否处于DOS值为零的区域中，来进行判定这个体系是绝缘性质的和半导性质的。

Figure 3. Comparison of state densities of unmodified TiO₂ and N-TiO₂ crystal planes

图3. 未改性TiO₂及N-TiO₂晶面的态密度对比图

态密度分析固有TiO₂和N-TiO₂的计算态密度(DOS)曲线如图3所示。可以发现，在本征TiO₂的DOS中，费米能级附近有一个较大的带隙，表明其半导体性质。与N-TiO₂的DOS相比，人们发现N原子掺杂后的总DOS发生了一些细微的变化。在费米能级附近，N原子的局部DOS与N-TiO₂的总DOS相似，表明N掺杂剂对整个系统的显着贡献。换句话说，TiO₂上的N原子在带隙内诱导了一些新的状态，从而导致N-TiO₂的DOS中出现了一些新出现的峰和变窄的带隙。带隙变窄这就够说明N掺杂TiO₂表面化学活性和电子迁移率得到了提高。

3.3. N-TiO₂吸附H₂S的参数计算

为了找到气体分子在N-TiO₂晶面上的稳定吸附位置，需要将一个H₂S和两个H₂S的硫原子分别以不同角度接近N-TiO₂，即分别以一个S原子、两个S原子靠近N原子，并计算每个结构的吸附参数。气体分子吸附于晶体表面的能力，是通过吸附能的大小体现的，吸附能同时也是指晶体表面与气体分子吸附过程中总体能量的变化，在本文吸附能用E_ad表示，计算公式如下：

$\text{Ead}=\text{ETIO2/}气体-\text{E}气体-\text{EN-TIO2}$ (1)

其中 $\text{ETIO2/}气体$ ， $\text{E}气体$ 和 $\text{EN-TIO2}$ 分别代表吸附系统的能量，气体分子的能量和N-TiO₂总能量。负 $\text{Ead}$ 表示相互作用是放热的，但也有可能自发发生。除外，还要考虑使用密立根总体的分析来得到Qt结果。正Qt表示电荷从分子转移到N-TiO₂，而负值表示相反的电子传输路径。

为了更好的了解吸附时前面和后面的电荷数量的变化，所以要计算出了晶状体的表面与气体分子吸附结构的密立根电荷分布。当气体分子与晶面吸附时与单个分子存在时的电荷变化用电荷转移量来进行表示。当电子从分子转移到晶面时电荷转移量为正值，反之为负值。气体分子与晶体表面在稳定的吸附结构中最近的距离表示为吸附距离。

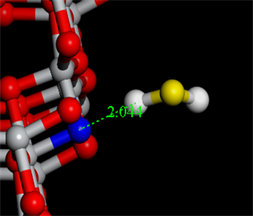
Figure 4. The structure of one and two H₂S adsorbed on the N-TIO ₂ crystal plane with S and one H atom in close proximity

图4. 一个和两个H₂S以S和一个H原子靠近的方式吸附于N-TiO₂晶面的结构

上图4为一个S原子、两个S原子和一个H原子分别靠近氮惨杂二氧化钛的吸附模型图，其中一个H₂S分子中的S原子和H原子与氮惨杂二氧化钛吸附的距离分别为2.040埃和2.044埃，两个H₂S分子中的两个S原子与氮惨杂二氧化钛吸附的距离分别为2.020埃和2.130埃。在MS软件中一般吸附原子的距离为2~4埃的为合适距离，因为如果距离过大，就会导致计算时间太长造成资源的浪费，如果吸附距离太小，就会有可能会发生化学吸附，从而影响吸附的结果。

根据Mulliken种群分析，我们发现N原子在吸附过程中的电荷转移时表现出真正的活化行为。具体而言，N掺杂剂中电荷的变化在吸附过程中对N的贡献很大。换句话说，N掺杂剂是抽出还是提供电子可以定性地确定被吸附物分子的电子损失或捕获行为。因此，可以得出结论，N掺杂剂为气体吸附到纳米载体上提供了具有强化学活性的活性部位，有望改善TiO₂表面的吸附性能。

考虑到参数，我们假设N-TiO₂与H₂S分子的相互作用较弱，其中范德华力在此过程中起主要作用，而对H₂S表现出很强的吸附能力，可以确定化学吸附。因此，可以推断出N-TiO₂对H₂S的吸附能力大于TiO₂。关于N掺杂物与原子内部气体分子之间的结合力，该顺序可以按以下顺序排列：S > H。这可证明N-TiO₂对H₂S具有更强的吸附能力。N-TiO₂与TiO₂相比，因此导致这些系统中的E_ad和Q_t更大。也就是说，N-TiO₂具有作为嵌入GIS中的气体吸附剂的潜力，以去除一些不良气体，从而确保这种电气设备的稳定运行。而且，如果这种材料具有一定的电子特性，使其可以用于检测这些气体，那么对它的勘探将是更好的选择。

Table 1. Surface characteristic parameters of N-TiO2 adsorbed by H2S

表1. H₂S吸附N-TiO₂表面特征参数

H₂S分子吸附N-TiO₂晶面的方式有三种，其吸附稳定结构如图4所示。吸附参数如表1所示，以一个S原子靠近吸附时，吸附能为−0.321 eV，吸附距离为2.040埃。以两个S原子靠近吸附时吸附能为−0.504 eV，吸附距离为2.020埃和2.130埃。以一个H原子靠近时吸附能为−0.021 eV，吸附距离为2.044埃。各个原子靠近吸附能大小比较为两个S原子大于一个S原子大于一个H原子。各个吸附中气体分子均得电子，吸附表面失电子，电子均从N-TiO₂晶体转移到气体分子，增大了电阻性，且电荷转移量相当，几乎为零。吸附距离大小相差不多。以上比较说明两个S原子比一个S原子及一个H原子靠近方式更稳定吸附于N-TiO₂晶面。

3.4. 前沿分子轨道理论分析

前沿分子轨道是一个叫做福井谦一的日本化学家所提出的，以分子的轨道可以能量的大小精确的分为不同大小的能级为根据，认为一个系统的化学反应发生与否与HOMO和LUMO是息息相关的，所以HOMO和LUMO是非常关键的，虽然其它的化学能量轨道对系统也有一定的影响，但是它们所造成的影响是很小的。

为了更好地理解由气体吸附引起的N-TiO₂的电导率变化，采用前沿分子轨道理论。在前沿分子轨道理论中有以下几个轨道，最高占据分子的分布轨道(Highest Occupied Molecular Orbital)，最低未占用分子轨道(Lowest Unoccupied Molecular Orbital)以及它们的能量，即HOMO，LUMO的能量以及HOMO和LUMO之间的能隙。

以分子前线轨道来看，吸附结构的能隙宽度可以通过计算N-TIO₂晶体吸附前和吸附气体分子之后的HOMO与LUMO来进行获取，并且根据1Hartree = 27.2114 eV的关系来进行换算。吸附后结构中的电子在整个HOMO与LUMO轨道之间转移的难易程度可以由能隙的宽度来反映，简而言之就是电子从价带顶跃迁到导带底端的能力。能隙越小，价带电子越容易跃迁到导带，让吸附基底的导电性能增强，使得气敏特性更好。

从表示计算体系的HOMO和LUMO分布的表2中可以看出，TiO₂计算体系是没吸附结构所以它的HOMO和LUMO能量分别为−7.3470 eV和−5.9320 eV，HOMO-LUMO为1.4150 eV。N-TIO₂计算体系也是没吸附结构所以它的的HOMO和LUMO能量分别为−7.3561 eV和−6.9471 eV，HOMO-LUMO为0.0408 eV。最高占据分子轨道和最低未占分子轨道分别可以表示为HOMO (Highest Occupied Molecular Orbital)和LUMO (Lowest Unoccupied Molecular Orbital)。因为前线轨道理论所规定的原则，这两者都叫做前线轨道，同时处在前线轨道上的电子称为前线电子。前线轨道HOMO与LUMO之间的能量差称为“能带隙”，这个能量差也就是HOMO-LUMO能级，一个分子是否很容易就被激发可以用HOMO与LUMO之间能带隙来进行衡量，根据带隙越小，分子越容易被激发,带隙越大，分子越难被激发的结论，对比数据TiO₂计算体系的HOMO-LUMO为1.4150 eV大于N-TIO₂的HOMO-LUMO为0.0408 eV，所以N-TiO₂比TiO₂具有更好的吸附性。

Table 2. Orbital parameters of stable structure on the surface of H2S adsorbed N-TIO2 crystal

表2. H₂S吸附N-TiO₂晶体表面稳定结构的轨道参数

根据H₂S系统，两个吸附位对于HOMO和LUMO具有相似的密度分布，如表2所示。H₂S的一个S原子吸附结构的HOMO和LUMO能量分别为−6.4571 eV和−6.1571 eV，HOMO-LUMO为0.3000 eV，可以看出它们的能带隙非常小，说明吸附效果良好。H₂S的一个H原子吸附结构的HOMO和LUMO能量分别为−5.4757 eV和−4.9566 eV，HOMO-LUMO为0.5191 eV，对比一个S原子能带隙增大了0.2191 eV，说明吸附效果降低了。H₂S的两个S原子吸附结构的HOMO和LUMO能量分别为−7.4896 eV和−7.2389 eV，HOMO-LUMO为0.2509 eV，在H₂S系统中吸附效果最好。

总而言之，可以得出结论，N-TiO₂是一种理想的传感材料，可以用于检测H₂S，因为它们存在时电导率会降低。

3.5. H₂S以不同原子靠近的方式吸附于N-TiO2晶面稳定结构的态密度

在分析态密度图的时候，要将DOS图和PDOS图放在一起，来进行对比分析。DOS图可以分析能隙的特性，比如，处于DOS所表示的值为零的那段区间的费米能级，说明了该体系可以是绝缘的体系或者说是半导体性质的体系；如果当体系是金属性质的体系时，那么就可以从图中看到有分波DOS跨过费米能级，并且PDOS图中的两个尖峰之间的DOS其实并不为零。赝能隙直接反映了该体系成键的共价性的强弱：越宽，说明共价性越强。

如图5所示H₂S以不同原子靠近的方式吸附于N-TiO₂晶面稳定结构的态密度，从气体分子态密度图中可以看出p轨道对气体分子的态密度贡献是最大的，因此将气体分子总的与p轨道的态密度一起展现在图里。

图5所示，在H₂S系统上，与N-TiO₂的DOS相比，两个系统的DOS在费米能级附近急剧转变，表明N-TiO₂对H₂S的良好吸附能力。另外，H₂S-S-TiO₂和之间的重叠面积大于H₂S-H-TiO₂之间的重叠面积，证实了N-S键的结合力比N-H键的结合力强。应当注意，相对于纯N-TiO₂系统，两个系统的带隙变大。该发现表明N-TiO₂的电导率在H₂S分子吸附后将下降。

总体而言，可以初步总结N-TiO₂对这些H₂S气体敏感性较好。也就是说，H₂S由于其化合价急剧增加，可以被视为对N-TiO₂最敏感的气体­导带隙，因为它引起N-TiO₂电导率的呈现出下降的趋势。

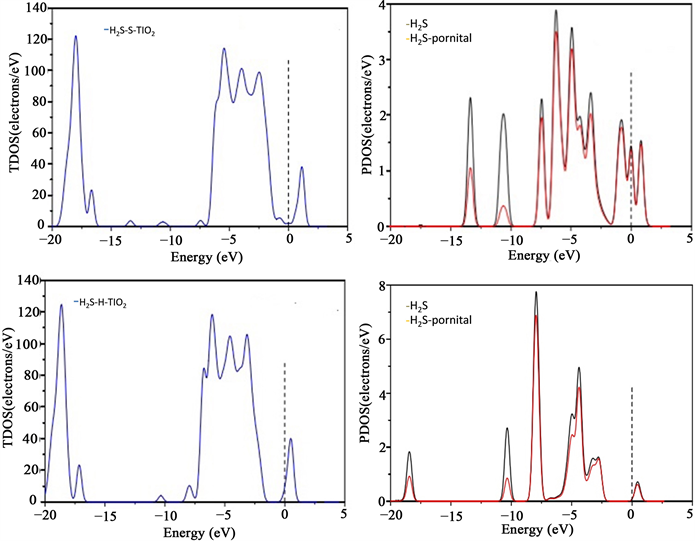
Figure 5. Density of states of H₂S adsorbed on the stable structure of N-TiO₂ crystal plane with different atomic approaches

图5. H₂S以不同原子靠近的方式吸附于N-TiO₂晶面稳定结构的态密度

4. 结论与展望

本文基于密度泛函理论，对SF₆分解气体在N掺杂TiO₂上的吸附进行了理论计算。为了全面了解这些吸附过程，考虑了Mulliken种群分析DOS和前沿分子轨道理论。结果表明：

1) N掺杂剂可以为TiO₂提供活性吸附位点，从而有效地提高了N-TiO₂对气体分子的吸附能力。

2) DOS和前沿分子轨道理论的结果一致表明，N-TiO₂对H₂S表现出良好的敏感性，N-TiO₂对气体的响应H₂S效果好。

3) N掺杂物与被吸附物分子中原子之间的结合力顺序可以按S > H的顺序排列。

TiO₂将成为一种选择性检测H₂S的前瞻性传感材料，因为它们呈现出不同的化学吸附度并导致不同的电导率变化。鉴于其对H₂S的更好敏感性，可以开发N-TiO₂气体传感器的某些应用。我们的计算可以为这种新型材料提供基本的吸附和传感机制，从而支持将其开发为电气工程领域中用于气体检测的化学传感器。对于GIS的运行状态估计，我们希望这样的初步研究可以为实验人员提供对这种新型材料的感应机制的进一步研究的初步了解。