1. 引言
随着近代科技的飞速发展,温室效应日益加重,气候变化成为人类面临的全球性问题。而我国在2020年9月明确提出“3060计划”,既是对于气候问题的积极应对,也是将其作为进一步推进经济高质量发展的重要抓手。在这样的战略背景下,对于广大企业而言,亟待有效地控制自身碳排放量与碳排放强度。而如何基于历史碳排放时序变化特征进一步对未来碳排放趋势进行预估对于企业的双碳规划与减碳工作有着至关重要的作用。
目前,主流对碳排放进行预测的方法有以下几种:基于IPAT分析模型的多元回归模型,基于STIRPIT分析模型的多元回归模型,Logistic模型,BP神经网络预测模型,GM(1,1)等。文献 [1] 使用了IPAT模型用于分析江西省碳排放因素,再以最小二乘法回归进行拟合,用于预测碳排放峰值,IPAT模型是表示人类活动对环境影响的一个简单的线性模型,虽然结构简洁,但也存在致命问题,如人口的数量,技术的发达与否,在不同的国家对环境所造成的影响程度是不同的,该模型无法确切表现出不同的背景下人类行为对环境的影响 [2] 。于是,Dietz and Rosa将其改善成了STIRPAT模型,文献 [3] 定量分析了江苏省能源消费碳排放与人口总量,技术先进程度,城镇化范围之间的关系,实验结果表明,控制人口和经济,提升科技发展,能有效降低江苏省的能源消费碳排放。文献 [4] 利用K-means聚类方法将中国各省区的碳排放类型分成5类,分析后,利用基本的Logistic模型预测结果,发现除宁夏自治区外结果较为精确,表明当年的碳排放与影响因素之间关系并不复杂。文献 [5] 用LDMI因素分解模型找出影响碳排放的主要因素,GM(1,1)全名是灰色系统预测,指用部分信息已知,部分信息未知的数据,去预测相应的目标,在碳排放预测方面正好具备一定的要求。
但是就预测结果与实际对比可以发现,以上方法的准确度仍然存在较大的提升空间。主要原因在于现阶段主流地碳排放预测大多需要额外的特征辅助,例如人口基数,技术发达程度,经济发展程度等指标,这些指标容易出现测算困难,“噪声”严重等问题,进而影响到预测效果。
针对上述研究的不足,本文提出了一种改进Prophet算法的预测算法。Prophet预测框架最初由Facebook在2017年提出 [6] ,用于预测时间序列相关的大规模数据。之所以选择Prophet算法,主要原因在于它的参数直观且容易调整,能够挖掘数据的潜在特殊特征,并对有趋势,周期,季节性变化的数据,相比于其他经典时间序列算法具有更大优势 [7] 。相较于ARIMA等传统算法,Prophet不需要使用者手动指定差分和季节性参数,能够自动适应多种季节性变化,提高拟合度;而与LSTM等深度学习算法相比,Prophet算法的模型更加直观,可解释性更高,对于中小规模的数据预测有着更好的效果。目前,Prophet算法已经被用于多个行业,商店价格预测 [8] ,交通运输量预测 [9] ,公路边坡变形分析 [10] ,表现出了极强的适用性和较高的准确率。本文尝试将Prophet算法用于工业领域,对某地区的碳排放进行相关分析与预测。以Prophet算法建立预测模型,在数据预处理过后,拟合Prophet算法进行预训练,再对短时间内的残差计算,将所有时间段的残差放入LSTM模型,进一步预测Prophet算法未来的残差,最后将预测出获得的残差与Prophet原预测值相加,计算得出改进后的预测值。
2. Prophet算法原理与数据预处理
2.1. Prophet算法原理
Prophet算法是一个加法回归模型,是对曲线不断拟合,迭代而形成的。整体模型由三个核心部分趋势项、季节项及假期项构成,公式如下:
(1)
2.2. 使用数据
本文使用数据为某地区2022年1月至2022年10月日碳排放数据。如图1为所示,为该地区每日用电碳排放总量变化图,在2022年1月,2022年2月,2022年7月时,经历了3段高峰,分别为225 kg与350 kg左右的日排放量,猜测是受气温变化的影响,用电碳排放数值在夏季和冬季有巨大的波动。
2.3. 数据清洗预处理
现有数据中存在着数据缺失,数据异常等问题。虽然prophet算法可以有效地忽视缺失值,但是对异常数据十分敏感,所以本文在预处理阶段,将数据表中明显脱离于总体数据变化趋势的值剔除,删除异常数据所用的方法为四分位距法。
2.4. 历史节假日标签设定
在Prophet算法中,假期项会对节假日单独处理,降低这些日期对模型的影响。虽然当前数据并未包含完整一年内的用电碳排放数据,但经测试,节假日仍然对模型有着一定影响。据此,本文针对节假日范围进行了设定,图2即为Prophet模型所设定的结果。其中,Lower_window和upper_window分别表示用电碳排放数据受节日前后影响的天数,lower_window不宜设置过高,否则会表明在假期多日前,数据已受其影响,从而导致数据失真。
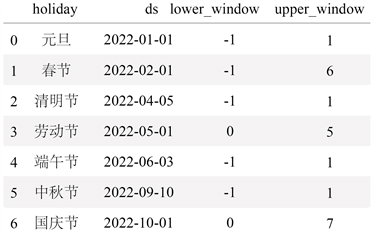
Figure 2. Historical holiday label settings
图2. 历史节假日标签设定
2.5. Prophet所拟合的变化趋势
图3从上至下分别为该地区用电碳排放数据整体变化趋势,受节假日影响、受星期影响的变化。

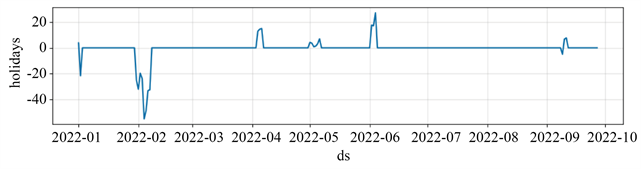

Figure 3. Prophet’s several terms trends
图3. Prophet各项趋势
由图3中第1张图可知,7月与8月间,该地区用电碳排放到达了最高峰,与原本数据变化相一致。第2张图,假期对数据变化趋势的影响较为明显。从第3张图的数据变化趋势来看,在周末的时候,用电碳排放量到达高峰,比较符合实际情况。
2.6. 算法检验指标
本文选用回归算法常用的RMSE (均方根误差)均方根误差和MAPE (平均绝对误差)作为模型拟合效果的检验指标。其中,RMSE用于判别预测值与样本真实值之间的差距,通常地,RMSE越小,代表模型的预测能力越好,其取值受到模型的规模和具体使用场景的影响,通常需要通过比较其他模型的RMSE来判断模型的预测效果。而MAPE一般用来判断模型预测值与真实值之间的相对误差,越接近0,则模型误差越低。
(2)
(3)
3. Prophet算法拟合
3.1. 初始参数设定
在Prophet的参数中,较为重要的参数主要是growth,change_points,,n_changepoints,periods,freq,changepoint_prior_scale;seasonality_prior_scale;holidays_prior_scale,分别为趋势模型,季节模型,假期模型之中的参数。growth有2个属性:linear和logistic。其中,linear用于线性回归,logistic用于逻辑回归,考虑到用电碳排放的数据前后间的时间关系,本文选择了logistic属性。
changepoints是数据趋势突然改变的一个特殊的时间点,默认为None,在本文的场景中,需要指定n_changepoints的值,以确定数据突变点的个数,本文设定为非空状态下的默认值,为25;changepoint_prior_scale代表模型的灵活度。值越大,模型对数据的拟合度越高,但是也会提高过拟合的风险,本文将通过循环确定最优取值(详见下文)。
Period,freq分别为待预测的日期长度(单位为天)和间隔,本文将period设定为‘D’,period指定为10,表示预测未来10天的数据。
Seasonality_prior_scale为季节性参数,值越大,表明数据受季节变化的影响越大,本文数据受季节影响,初始设定为10,后续通过循环进行优化调整。
Holidays_prior_scale为节假日参数,对变化趋势影响不大,默认为10,本文不做调整。
3.2. 最优参数循环确定
本文设定自动调整的参数为c = changepoint_scale,s = seasonality_prior_scale。步骤如图4所示:
1) 设定默认参数为c = 0.01,s = 1.
2) 输出用电碳排放预测结果,即[d1, d2, d3, ..., dn–4]所对应的yhat的值,计算RMSE
3) 将当次结果保存至缓存。
4) 调整c和s的值,补偿输出档次循环的预测结果, 计算RMSE。
5) 将当次RMSE的值与缓存中的RMSE进行比较,如果比已储存的RMSE更小,则将当前RMSE存入缓存。
6) 循环结束,得出最佳参数c = 0.95,s = 10
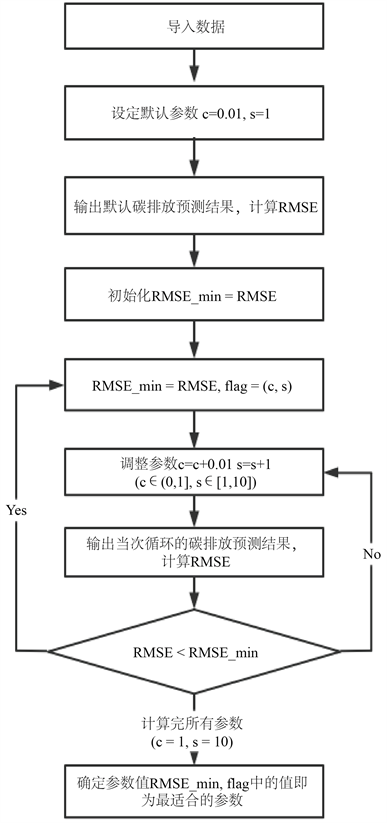
Figure 4. The flow path of ensuring prophet parameters
图4. 确定Prophet参数的流程
3.3. 基于可视化分析的算法调整方向确定
图5即为调整参数过后的Prophet算法,由图中可知,在数据前半部分,Prophet与真实数据拟合效果尚可,但在后半段,Prophet趋势变得平缓,不再波动,经分析,确定原因是changepoint_prior_scale最终取值定为0.8 (进一步调大存在过拟合风险),而在数据的后半段,有较多的突变点,影响了模型的预测效果,说明单一的Prophet算法拟合对于这种数据较短(不足一年的周期),拐点较多的数据集仍然存在着不足之处,因此本文进一步考虑了以LSTM神经网络拟合残差的方式进行算法的补充优化。
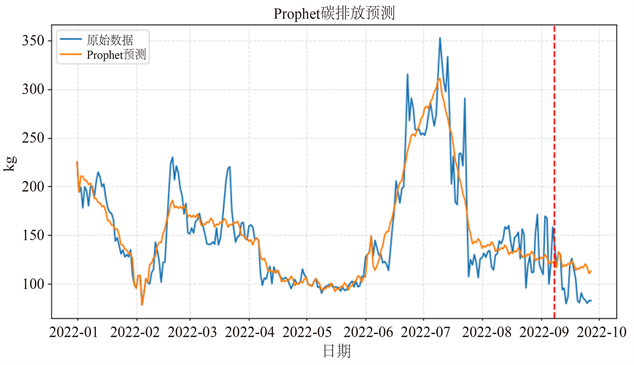
Figure 5. Prophet prediction on the carbon emissions
图5. Prophet碳排放预测
4. 基于LSTM改进的Prophet算法思路说明
4.1. LSTM算法原理
LSTM (Long Short-Term Memory)长短期记忆网络,是一种时间循环记忆网络。基于RNN (Recurrent Neural Network)循环神经网络改造,解决了RNN长期依赖的问题,而能够将其用于时间序列的预测。
4.2. 基于LSTM的Prophet算法改进
为了进一步提升Prophet的预测精度,本文提出了一种基于LSTM改进的Prophet算法。算法的流程如下,如图6所示:
1) LSTM将40天划分为一个时间段,通过前30天的用电碳排放数值预测后10天的值,残差为Prophet的预测值减样本真实值。
(4)
2) 将第1个时间段起止时间向后推移一天,此时,求出第2个时间段的残差,此时间段所对应的用电碳排放数据即为建立LSTM模型所需的第2个样本。
3) 将时间序列数据转换为可监督数据,建立一个新的数据表,特征值Data_X为前30天的数据,标签值Data_Y为后10天的残差.
4) 将该数据表7/3分,分为训练集与测试集,分别得到样本数为160和70。测试集用来测试模型的预测效果,以调整神经网络的参数。
5) 将训练集归一化放入模型,以提高预测精度。测试集同时进行归一化,并且使用训练集中的最大值和最小值作为归一化的参数进行计算,避免预测集的数据泄漏到测试集,影响模型的可用性。
6) 将已归一化的训练集的特征转换成LSTM神经网络的格式[samples, time steps, features],其中samlpes为样本总数,表明从原始数据分离出的时间段(一个时间段为一个样本)的数量,此处为161,timestep为时间跨度,即一个样本中用于观测的天数,此处为30,features为特征个数,在该时间序列中,特征只有30天内的用电碳排放数值,所以特征为1。所以新的数据集特征为[161, 30, 1]。利用网格调参,调整神经网络的参数,分别设置epochs设置在在[10, 15, 20, 25, 30]之间,batch_size设置在[2, 4, 6, 8, 16, 32]之间,分别反归一化后,得到所有模型的平均MAPE与RMSE,基于检验指标得到最佳参数。
新模型的预测结果的最后一条数据即为单一的Prophet未来的预测残差,将二者相加,计算出新的预测结果,并进一步与原预测结果比较。

Figure 6. Ensemble flow path of improving prophet algorithm
图6. 整体改进Prophet算法流程
5. 预测结果对比分析
图7为Prophet算法为某地区用电碳排放预测的结果,本文首先以可视化的方式,同时与单一的Prophet与LSTM算法进行了比较。如图6中所示,在测试集中随机选取了9个时间片段,分别对3种算法的准确度进行比较,蓝色曲线为原始数据,橙色曲线为Prophet的预测数据,绿色曲线为LSTM预测数据,红色曲线为LSTM调整后的Prophet预测数据。
可以看出,对这些时间段进行预测时,单一的LSTM效果最差,与原始数据的偏离程度较高。单一Prophet与改进后的Prophet曲线接近,但在大部分的时间段中,改进后的Prophet效果比单一的Prophet效果更好。
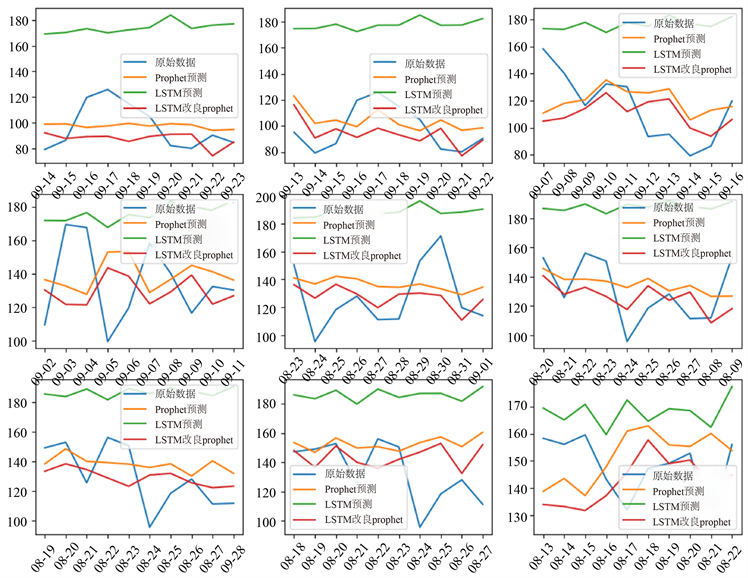
Figure 7. Prediction results of three algorithms in several time periods
图7. 三种算法几个时间段内的预测结果
进一步的,本文通过计算MAPE和RMSE这两个检验指标,对三种算法的拟合效果进行量化比较,结果如表1所示。从结果来看,基于LSTM改进后的prophet算法预测效果相比于单一的Prophet和LSTM都有显著的优势,其中,MAPE下降约12%与82%,RMSE下降5%与36%。
6. 总结
本文提出了一种基于改进Prophet的地区用电碳排放预测模型,并形成了以下结论:
1) Prophet算法能适用于时间序列的地区用电碳排放预测,但是当时序数据存在阶段性突变情况时,Prophet的拟合效果会有比较明显的下滑;
2) LSTM在观测短时间内的数据时,与Prophet等时序模型相比,对观测数据的拟合效果较差,导致预测结果与实际值偏差较远。
3) 结合LSTM对残差的拟合,能够进一步有效改进Prophet算法,具体而言,先通过Prophet算法进行短时间的预测,算出预测结果与实际值的残差,再将所有时间段内的残差放入LSTM进行拟合,最后将LSTM预测出的残差,附加到Prophet的预测值中,得到改进后的预测值,其预测结果会明显优于单一的Prophet算法。
参考文献