钻石项链图Nk的点被多重集可区别的E-全染色(2 ≤ k ≤ 165)

E-Total Coloring of Nk Which Is Vertex-Distinguished by Multiple Sets (2 ≤ k ≤ 165)

摘要: 利用反证法和构造具体染色的方法，讨论了钻石项链图Nk的顶点被多重集可区别的E-全染色。给出了钻石项链图Nk的相应染色方案，构造了具体的钻石项链图Nk的点被多重集可区别的E-全染色，其中2 ≤ k ≤ 165。

Abstract: In this paper, by using the method of contradiction and the method of constructing concrete col-oring, we discuss E-total coloring of Nk which is vertex-distinguished by multiple sets. The corre-sponding colorings of Nk are presented, and the E-total chromatic numbers of vertex-distinguished Nk with multiple sets are obtained, which 2 ≤ k ≤ 165.

1. 引言

图的点可区别正常边染色在文献 [1] 中提出的。文献 [2] 给出了完全图和星的合成的点可区别正常边色数。关于无爪3-正则图的研究 [3] [4] 已经有不少，其中在文献 [5] 中探讨了特殊的无爪3-正则图钻石项链图。图的点可区别IE-全染色这一概念在文献 [6] 中被提出。并且点可区别IE-全染色在文献 [7] [8] [9] [10] 中针对完全三部图展开研究。上述文献都是基于图的点被非多重集可区别全染色所做出的工作，而我们在本文中所提出的为图的点被多重集可区别的E-全染色，并给出了钻石项链的染色的方案，构造了具体钻石项链 $N_k\left(\text{2}\le k\le \text{165}\right)$ 的点被多重集可区别的E-全染色。

设v是G的一个顶点，v的度是点关联的边数，若对所有 $v\in \text{V}$ 都有d(v) = k，则称G为k-正则的。任意两个顶点都邻接的图称为完全图，将含n个顶点的完全图记为K_n。特别的，K₃称为三角形，K₄去掉一个边称作钻石。

对于一个整数k ≥ 2，令N_k表示如下定义的连通的3-正则图，取k个不交的钻石 $D_1,D_2,\cdots ,D_k$ ， $V\left(D_i\right)=\left\{a_i,b_i,c_i,d_i\right\}$ 且 $a_i{b}_i$ 是 $D_i$ 中去掉的边。令N_k是由这k个钻石通过不交的并，并添加边 $\left\{a_i{b}_{i+1}|i=1,2,\cdots ,k-1\right\}$ 和 $a_k{b}_1$ 构成的图。将N_k叫做一个k个钻石的钻石项链(图1)。

Figure 1. A diamonds

图1. 一个钻石

图G的VE-全染色是指使得每条关联边与它的端点染以不同的颜色(I条件)的一个VE-全染色。图G的E-全染色是指使得相邻顶点染以不同色(V条件)，每条关联边与它的端点染以不同的颜色(I条件)的一个E-全染色。图G使用了k种颜色的VE-全染色叫做图G的k-VE-全染色，图G使用了k种颜色的E-全染色叫做图G的k-E-全染色。若f为图G的E-全染色。对于任意的 $x\in \text{V}\left(\text{G}\right)$ ，用 $\tilde{C}\left(x\right)$ 表示点x的色以及与x相关联的边的颜色构成的多重集。称 $\tilde{C}\left(x\right)$ 为点x的多重色集合或色集合。显然有 $\left|\tilde{C}\left(x\right)\right|=d_G\left(x\right)+1$ ，其中， $d_G\left(x\right)$ 表示图G中点x的度。若对任意的 $u,v\in \text{V}$ ， $u\ne v$ ，总有 $\tilde{C}\left(u\right)\ne \tilde{C}\left(v\right)$ ，则称f是点被多重色集合可区别的。

将 ${\tilde{\chi }}_{vt}^e\left(G\right)$ 称为图G的点被多重集可区别的E-全色数， ${\tilde{\chi }}_{vt}^{ve}\left(G\right)$ 称为图G的点被多重集可区别的VE-全色数。 ${\tilde{\chi }}_{vt}^e\left(G\right)$ = min{k|G存在点被多重集可区别的k-E-全染色}。 ${\tilde{\chi }}_{vt}^{ve}\left(G\right)$ = min{k|G存在点被多重色集合可区别的k-VE-全染色}。

设图G中存在使用了l种色的点被多重色集合可区别的E-全染色， $n_i$ 为i度点的个数， $A_j$ 为从l-1种颜色里有重复的取出i + 1种颜色使j只出现1次的组合， $j=\text{1},\text{2},\text{3},\cdots ,l$ 。其中 $\left|A_j\right|$ 为从l-1种颜色里有重复的取出i种颜色的组合的个数。

设 $\tilde{\eta }\left(G\right)$ 表示满足下面两条件对一切使得 $\delta \le i\le \Delta$ 的i都成立的正整数l的最小值，分为以下两个情形：

情形1 l ≥ i + 2。

$\begin{array}{l}\left|A_1\cup A_2\cup A_3\cup \cdots \cup A_{i+1}\right|\\ =\left(\begin{array}{c}l-1\\ 1\end{array}\right)\left(\begin{array}{c}l+i-2\\ i\end{array}\right)-\left(\begin{array}{c}l-1\\ 2\end{array}\right)\left(\begin{array}{c}l+i-4\\ i-1\end{array}\right)+\left(\begin{array}{c}l-1\\ 3\end{array}\right)\left(\begin{array}{c}l+i-6\\ i-3\end{array}\right)+\cdots \\ +{\left(-1\right)}^i\left(\begin{array}{c}l-1\\ i-1\end{array}\right)\left(\begin{array}{c}l-i+2\\ 2\end{array}\right)+{\left(-1\right)}^{i+1}\left(\begin{array}{c}l-1\\ i+1\end{array}\right)\left(\begin{array}{c}l-i-3\\ 0\end{array}\right)\ge n_i;\end{array}$

情形2 l ≤ i + 1。

$\begin{array}{l}\left|A_1\cup A_2\cup A_3\cup \cdots \cup A_{l-2}\right|\\ =\left(\begin{array}{c}l-1\\ 1\end{array}\right)\left(\begin{array}{c}l+i-2\\ i\end{array}\right)-\left(\begin{array}{c}l-1\\ 2\end{array}\right)\left(\begin{array}{c}l+i-4\\ i-1\end{array}\right)+\left(\begin{array}{c}l-1\\ 3\end{array}\right)\left(\begin{array}{c}l+i-6\\ i-3\end{array}\right)+\cdots \\ +{\left(-1\right)}^{l-2}\left(\begin{array}{c}l-1\\ l-3\end{array}\right)\left(\begin{array}{c}i-l+6\\ i-l+4\end{array}\right)+{\left(-1\right)}^{l-1}\left(\begin{array}{c}l-1\\ l-2\end{array}\right)\left(\begin{array}{c}i-l+3\\ i-l+3\end{array}\right)\ge n_i;\end{array}$

命题1 ${\tilde{\chi }}_{vt}^e\left(G\right)\ge {\tilde{\chi }}_{vt}^{ve}\left(G\right)\ge \tilde{\eta }\left(G\right)$ 。

2. 准备工作

以下定义十一种剖分：

设N_p是一个点被多重集可区别的q-E-全染色f_p的p阶钻石项链，其q种颜色是 $\text{1},\text{2},\cdots ,q$ 。

O₁型剖分运算：设i，j，s，h，t是五种互不相同的颜色， $i,j,s,t,h\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,j,j}，{j,t,i,i}{i,j,s,t}，{i,j,h,t}均不是N_p外围圈上的任意点在f_p下的色集合，所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;t] -O₁型剖分运算是指将N_p按照图2所示的方法变成N_p+1的过程。

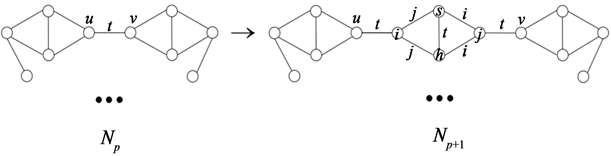
Figure 2. The color of vertex u is not i, and the color of vertex v is not j

图2. 点u的色不是i，点v的色不是j

O₂型剖分运算：设i,j,s,h,t,r是六种互不相同的颜色， $i,j,s,h,t,r\in \left\{1,2,3,\cdots ,q\right\}$ 。且{i,r,t,t},{j,r,t,t}{s,r,t,t},{h,r,t,t}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;r,t]-O₂型剖分是指将N_p按照图3所示的方法变成N_p+1的过程。

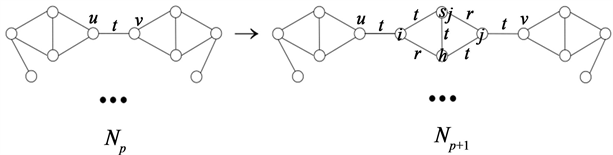
Figure 3. The color of vertex u is not i, and the color of vertex v is not j

图3. 点u的色不是i，点v的色不是j

O₃型剖分运算：设i,j,s,h,t是五种互不相同的颜色， $i,j,s,h,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,j,j}，{j,t,i,i}{i,j,s,t}，{i,j,s,h}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;t]- O₃型剖分是指将N_p按照图4所示的方法变成N_p+1的过程。

图4. 点u的色不是i，点v的色不是j

O₄型剖分运算：设i,j,s,h,r是五种互不相同的颜色， $i,j,s,h,r,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,j,j}，{i,t,r,r}，{s,r,i,j}，{h,r,i,j}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,s,h;j,r,t]-O₄型剖分是指将N_p按照图5所示的方法变成N_p+1的过程。

图5. O₄型剖分运算

O₅型剖分运算：设i,j,s,h,是四种互不相同的颜色， $i,j,s,h,r,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,j,j}，{j,t,i,i}{s,r,i,j},{h,r,i,j}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;r,t]- O₅型剖分是指将N_p按照图6所示的方法变成N_p+1的过程。

O₆型剖分运算：设i,j,s,h,是四种互不相同的颜色， $i,j,s,h,m,n,r,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,r,m}，{j,t,r,m}{s,r,m,n}，{h,r,m,n}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;m,n,r,t]- O₆型剖分是指将N_p按照图7所示的方法变成N_p+1的过程。

图6. 点u的色不是i，点v的色不是j

图7. 点u的色不是i，点v的色不是j

S₁型剖分运算：设i,j,s,h,m,n,r,t是八种互不相同的颜色 $i,j,s,h,m,n,r,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,t,t}，{i,s,t,t}，{i,h,t,t}，{i,j,t,t}，{j,t,r,r}，{r,t,i,i}，{m,i,t,r}，{n,i,t,r}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h,m,n;r,t]-S₁型剖分是指将N_p按照图8所示的方法变成N_p+2的过程。

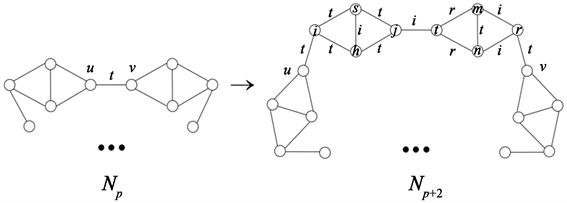
Figure 8. The color of vertex u is not i, and the color of vertex v is not r

图8. 点u的色不是i，点v的色不是r

S₂型剖分运算：设i,j,s,h,m,n,t是七种互不相同的颜色 $i,j,s,h,m,n,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,t,t}，{s,t,t,t}，{h,t,t,t}，{i,j,t,t}，{m,i,t,t}，{j,t,i,i}，{n,t,i,i}，{m,t,i,i}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h,m,n;t]-S₂型剖分是指将N_p按照图9所示的方法变成N_p+2的过程。

S₃型剖分运算：设i,j,s,h,r,t是六种互不相同的颜色 $i,j,s,h,r,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,r,r,t}，{s,r,r,t}，{h,r,r,t}，{r,j,t,t}，{r,i,t,t}，{s,r,t,t}，{h,r,t,t}，{j,t,r,r}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;r,t]-S₃型剖分是指将N_p按照图10所示的方法变成N_p+2的过程。

Figure 9. The color of vertex u is not i, and the color of vertex v is not m

图9. 点u的色不是i，点v的色不是m

图10. 点u的色不是i，点v的色不是j

T₁型剖分运算：设i,j,s,t是四种互不相同的颜色 $i,j,s,t,r\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,j,j}，{s,t,j,j}，{t,j,j,j}，{r,j,t,t}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,r;t]-T₁型剖分是指将N_p按照图11所示的方法变成N_p+1的过程，其中r可以为i。

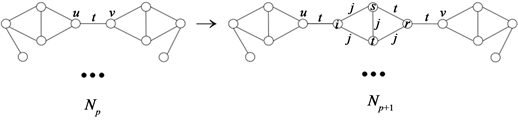
Figure 11. The color of vertex u is not i, and the color of vertex v is not r

图11. 点u的色不是i，点v的色不是r

T₂型剖分运算：设i,j,s,h,t是五种互不相同的颜色 $i,j,s,h,r,t\in \left\{\text{1},\text{2},\text{3},\cdots ,q\right\}$ 。且{i,t,r,r}，{s,r,r,r}，{j,t,r,r}，{h,r,r,r}均不是N_p外围圈上的任意点在f_p下的色集合。所谓对N_p的染有颜色t的一条边uv实施一次[i,j,s,h;r,t]-T₂型剖分是指将N_p按照图12所示的方法变成N_p+1的过程,其中r可以为t。

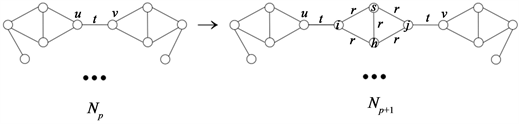
Figure 12. The color of vertex u is not i, and the color of vertex v is not j

图12. 点u的色不是i，点v的色不是j

3. 主要结论及其证明

定理1 $N_k\left(\text{2}\le k\le \text{165}\right)$ 的点被多重集可区别的E-全染色

${\tilde{\chi }}_{vt}^e\left(N_k\right)=\{\begin{array}{l}4,2\le k\le 5;\\ 5,6\le k\le 12;\\ 6,13\le k\le 23;\\ 7,24\le k\le 42;\\ 8,43\le k\le 68\\ 9,69\le k\le 110\\ 10,111\le k\le 165\end{array}$

证明 根据命题1与 $N_k\left(\text{2}\le k\le \text{165}\right)$ 的性质， $N_k\left(\text{2}\le k\le \text{165}\right)$ 中3度点有n个，则有

$\tilde{\eta }\left(N_k\right)=\min \left\{l|\left(\begin{array}{c}l-1\\ 1\end{array}\right)\left(\begin{array}{c}l+1\\ 3\end{array}\right)-\left(\begin{array}{c}l-1\\ 2\end{array}\right)\left(\begin{array}{c}l-1\\ 2\end{array}\right)+\left(\begin{array}{c}l-1\\ 3\end{array}\right)\left(\begin{array}{c}l-3\\ 1\end{array}\right)-\left(\begin{array}{c}l-1\\ 4\end{array}\right)\ge 4k\right\}$ ;

$k\le \lfloor \frac{\left(\begin{array}{c}l-1\\ 1\end{array}\right)\left(\begin{array}{c}l+1\\ 3\end{array}\right)-\left(\begin{array}{c}l-1\\ 2\end{array}\right)\left(\begin{array}{c}l-1\\ 2\end{array}\right)+\left(\begin{array}{c}l-1\\ 3\end{array}\right)\left(\begin{array}{c}l-3\\ 1\end{array}\right)-\left(\begin{array}{c}l-1\\ 4\end{array}\right)}{4}\rfloor$ 。

假设N_k存在点被多重集可区别的l-E-全染色f_k $\left\{\text{1},\text{2},\cdots ,l\right\}$ ，其中一个钻石D_i存在点被多重集可区别的l-E-全染色f_k $\left\{\text{1},\text{2},\cdots ,l\right\}$ ，不妨设序列：

$\begin{array}{l}{f}_{D_i}=(f_k\left(b_{i-1}{a}_i\right)f_k\left(a_i\right)f_k\left(c_i{a}_i\right)f_k\left(d_i{a}_i\right),f_k\left(a_i{c}_i\right)f_k\left(c_i\right)f_k\left(c_i{d}_i\right)f_k\left(c_i{b}_i\right),\\ f_k\left(a_i{d}_i\right)f_k\left(d_i\right)f_k\left(c_i{d}_i\right)f_k\left(d_i{b}_i\right),f_k\left(c_i{b}_i\right)f_k\left(b_i\right)f_k\left(d_i{b}_i\right)f_k\left(b_i{a}_{i+1}\right)),i=1,2,\cdots ,k-1\end{array}$

则 $f_k=\left(f_{D_1};f_{D_2};\cdots ;f_{D_k}\right)$ 。

情形1 $\text{2}\le k\le \text{5}$ 。

首先证明当k = 2时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)>3$ 。(尽管此时 $\tilde{\eta }\left(N_k\right)=3$ ，但 ${\tilde{\chi }}_{vt}^e\left(N_k\right)>3$ 。)

假设N_k存在顶点被多重集点可区别染色的3-E-全染色h。若一个4-子集能够成为一个顶点的色集合，必须具备“某一种颜色在该4-子集里仅出现一次”的性质。所以能够成为顶点的色集合的4-子集，只可能是以下9个子集：

{1,1,1,2}，{1,1,1,3}，{2,2,2,1}，{2,2,2,3}，{3,3,3,1}，{3,3,3,2}，{1,2,3,1}，{1,2,3,2}，{1,2,3,3}；

则N₂只能为以下模式： $h_2=\left(3132,3213,2312,3123;3231,3123,1321,3213\right)$ 。

显然 $\text{C}\left(a_1\right)=\text{C}\left(b_2\right)$ ，故这两点无法可区别，矛盾。

综上可得， ${\tilde{\chi }}_{vt}^e\left(N_k\right)>3$ 。

其次，当 $\text{3}\le k\le \text{6}$ 时， $\tilde{\eta }\left(N_k\right)=4$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 4$ 。但当k = 6时， $\tilde{\eta }\left(N_k\right)>4$ 。

假设N₆存在顶点被多重集点可区别染色的4-E-全染色。将能够成为一个顶点的色集合的25个4-子集分为两类，一类形如iiij，其中i,j = 1,2,3,4且i≠j共12个，剩余的13个4-子集成为第二类。之后，若一个钻石存在顶点被多重集点可区别染色的4-E-全染色g，这样的g可分为A，B，C，D，E五类模块，其中i,j,s,t为四种不同的颜色，模块分别为：

A类模块由三个一类4-子集，一个二类4-子集组成；则g = (isii,itii,ijii,isir)，其中r = t或j。

B类模块由两个一类4-子集，两类个二类4-子集组成；则g = (ijii,itis,isii,sjir)，其中r = s或i。

C类模块由两个一类4-子集，两类个二类4-子集组成；则g = (isii,ijrs,itrs,siss)，其中r = s或i。

D类模块由一个一类4-子集，三类个二类4-子集组成；则g = (kthi,hjir,isii,rtim)，其中r = s或i,h = s或i,r ≠ h，k = i,j,s，m = i,j,s，k与m可以相同。

E类模块由四个二类4-子集组成；

再将这五个模块结合为六个钻石，最后将这六个钻石按照边 $b_{i-1}{a}_i$ 和边 $b_i{a}_{i+1}$ 的颜色串成圈(颜色相同的可相邻，反之不可)，分为以下几个情形：

情形1.1 包含4个A类模块，2个E类模块

若N₆包含4个A类模块，不妨设4个A模块所用的第二类4-子集为{1,1,2,3}，{2,2,3,4}，{1,3,3,4}，{1,3,4,4}，且剩余的9个4-子集中的4个4-子集可组合为E模块的色集合 (3213,1341,3144,1243)，故剩余{1,2,2,3}，{1,1,2,4}，{1,2,2,4}，{2,3,3,4}，{2,3,4,4}其中有4个4-子集组合起来必会成为一个钻石的色集合。

若这个钻石的色集合含{1,1,2,4}，令顶点a₆的顶点着色为2，a₆外接边的颜色为1，则顶点b₆的色集合需要颜色2，颜色4，颜色1皆出现一次。但{1,2,2,3}中颜色4不出现，{2,3,3,4}中颜色1不出现。

令顶点a₆的顶点着色为4，a₆外接边的颜色为1，则顶点c₆的色集合只能为{1,3,2,2}，故顶点d₆的色集合需要出现颜色2两次，但剩余的三个集合都不满足。

令顶点a₆的顶点着色为4，a₆外接边的颜色为2，则顶点c₆的色集合只能为{1,3,2,2}，顶点d₆着色需满足V条件，并且色集合需要出现颜色1一次，颜色2一次，但剩余的三个集合都不满足。

令顶点a₆的顶点着色为2，a₆外接边的颜色为4，则顶点c₆的色集合只能为{1,4,2,2}，顶点d₆的色集合只能为{1,3,2,2}，故顶点b₆的色集合需要出现颜色2两次，但剩余的两个集合都不满足。

故这个钻石的色集合不含{1,1,2,4}，因此这个钻石的色集合只能包含{1,2,2,3}，{1,2,2,4}，{2,3,3,4}，{2,3,4,4}。

若这个钻石的色集合含{1,2,2,4}，令顶点a₆的顶点着色为4，a₆外接边的颜色为2，则顶点c₆的色集合只能为{1,3,2,2}，故顶点d₆的色集合需要出现颜色2两次，但剩余的两个集合都不满足。

令顶点a₆的顶点着色为1，a₆外接边的颜色为2，若顶点c₆的色集合为{4,2,3,3}，则顶点d₆的色集合只能为{2,1,3,2}，故顶点b₆的色集合需要出现颜色2一次，颜色3一次且满足I条件，但{2,3,4,4}不满足上述条件。若顶点c₆的色集合为{4,2,3,4}，则g = {2142,4234,2132,4324}，因C(a₆) = {2142}，C(b₆) = {4324}，但C(a₁) = {1311}所以无法串成圈。若顶点c₆的色集合为{4243}，故顶点d₆的色集合需要出现颜色2一次，颜色4一次且满足I条件，但{2,3,3,4},{1,2,2,3}不满足上述条件。

令顶点a₆的顶点着色为1，a₆外接边的颜色为4，若顶点c₆的色集合{2,3,1,2}，故顶点d₆的色集合需要出现颜色1一次，颜色2一次，但剩余的两个个集合都不满足。若顶点c₆的色集合{2,3,2,1}，故顶点d₆的色集合需要出现颜色2两次，但剩余的两个集合都不满足。若顶点c₆的色集合{2,4,3,3}，故顶点d₆的色集合需要出现颜色2一次，颜色3一次且满足I条件，但剩余的两个集合都不满足。若顶点c₆的色集合{2,3,4,4}，故顶点d₆的色集合需要出现颜色2一次，颜色4一次且满足I条件，但剩余的两个集合都不满足。

令顶点a₆的顶点着色为4，a₆外接边的颜色为1，若顶点c₆的色集合{2,3,1,2}，故顶点d₆的色集合需要出现颜色1一次，颜色2一次，但剩余的两个集合都不满足。若顶点c₆的色集合{2,3,2,1}，故顶点d₆的色集合需要出现颜色2两次，但剩余的两个集合都不满足。若顶点c₆的色集合{2,4,3,3}，则不满足V条件。若顶点c₆的色集合{2,3,4,4}，故顶点d₆的色集合需要出现颜色2一次，颜色4一次且满足I条件，但剩余的两个集合都不满足。

故在情形1.1中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.2 包含3个A类模块，1个B类模块，1个D类模块，1个E类模块

若N₆包含3个A类模块，不妨设3个A模块所用的第一类4-子集为iiij，其中i,j = 1,2,3且i ≠ j，第二类4-子集为{1,1,2,3}，{2,2,1,3}，{1,3,3,2}。

若{4,4,4,1}与{4,4,4,2}与两个第二类4-子集组合为B模块，{4,4,4,3}与三个第二类4-子集组合为D模块。B模块的色集合不妨为{4144,4342,4244,2142}，D模块的色集合只能为{4134,3243,4344,3143}，E模块的色集合只能为{1412,1243,2142,3422}，之后将得到的六个模块串成一个链，但因C(b₆) = {3143}，但C(a₁) = {1311}所以无法串成圈。

若{4,4,4,1}与{4,4,4,3}与两个第二类4-子集组合为B模块，{4,4,4,2}与三个第二类4-子集组合为D模块。B模块的色集合不妨为{3134,3244,4344,4144}，D模块的色集合只能为{4124,2342,4244,2142}，E模块的色集合只能为{1413,1342,3143,2433}，之后将得到的六个模块串成一个链，但因C(b₆) = {2142}，但C(a₁) = {1311}所以无法串成圈。

若{4,4,4,2}与{4,4,4,3}与两个第二类4-子集组合为B模块，{4,4,4,1}与三个第二类4-子集组合为D模块。B模块的色集合不妨为{4244,4143,4344,2342}，D模块的色集合只能为{1314,1241,4144,1434}，E模块的色集合只能为{2124,2433,4234,3142}，之后将得到的六个模块串成一个链，但因C(a₆) = {4244}，C(b₆) = {2342}，但C(a₁) = {1311}所以无法串成圈。

故在情形1.2中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.3 包含2个A类模块，2个B类模块，1个C类模块，1个E类模块

若N₆包含2个A类模块，不妨设2个A模块所用的第一类4-子集为iiij，其中i,j = 1,2且i ≠ j，第二类4-子集为{1,1,2,3}，{2,2,1,3}。

只能{3,3,3,1}与{3,3,3,2}与两个第二类4-子集组合为一个B₁模块，{4,4,4,1}与{4,4,4,2}与两个第二类4-子集组合为一个B₂模块，{3,3,3,4}与{4,4,4,3}与两个第二类4-子集组合为C模块。

若C模块的色集合为{3433,1344,2344,4344}，B₂模块的色集合中的{1,3,4,4}，{2,3,4,4}已被使用，无法组合为B₂模块的色集合。

若C模块的色集合为{3433,1334,2334,4344}，B₁模块的色集合中的{1,3,3,4}，{2,3,3,4}已被使用，无法组合为B₁模块的色集合。

C模块的色集合有且仅有这两种，故在情形1。3中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.4 包含2个A类模块，1个C类模块，3个D类模块

若N₆包含2个A类模块，不妨设2个A模块所用的第一类4-子集为iiij，其中i,j = 1,2且i ≠ j，第二类4-子集为{1,1,2,3}，{2,2,1,3}。{3,3,3,4}与{4,4,4,3}与两个第二类4-子集组合为C模块。{3,3,3,1}，{3,3,3,2}，{4,4,4,1}，{4,4,4,2}从中取三个与三个第二类4-子集组合为D₁,D₂,D₃模块。

若C模块的色集合为{3433,1344,2344,4344}，D₁模块的色集合为{1431,1233,3133,3431}，D₂模块的色集合为{2124,2342,4244,2144}，D₃模块的色集合为{1431,1233,3133,3431}。剩余的第二类4-子集为{1,1,2,4}，{2,3,3,4}，{1,2,3,4}，因{1,1,2,4}中没有颜色3，故只能由{4,4,4,1}与上述三个子集组合。若{1,1,2,4}是a₆的色集合，故顶点c₆的色集合只能是{1,3,4,2}，故顶点b₆的色集合需要出现颜色2一次，颜色4一次，但剩余的两个集合都不满足。若{1,1,2,4}是c₆的色集合，故顶点a₆的色集合只能是{2,3,1,4}，故顶点b₆的色集合需要出现颜色1一次，颜色4一次，但剩余的两个集合都不满足。

故在情形1.4中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.5 包含2个A类模块，2个B类模块，2个D类模块

若N₆包含2个A类模块，不妨设2个A模块所用的第一类4-子集为iiij，其中i,j = 1,2且i ≠ j，第二类4-子集为{1,1,2,3}，{2,2,1,3}。{3,3,3,1}与{3,3,3,2}与两个第二类4-子集组合为B₁模块，{4,4,4,1}与{4,4,4,2}与两个第二类4-子集组合为B₂模块，{3,3,3,4}，{4,4,4,3}分别与三个第二类4-子集组合为D₁，D₂模块。

则B₁的色集合为{3133,3432,3233,2133}，B₂的色集合为{4144,4324,4244,2142}，余{1,1,2,4}，{1,2,4,4}，{1,1,3,4}，{1,3,3,4}，{1,3,4,4}，{2,2,3,4}，{1,2,3,4}与{3,3,3,4}，{4,4,4,3}组合为D₁，D₂模块，其中{1,1,3,4}因不满足V条件，故无法与其组合。则余下的六个第二类4-子集必能与{3,3,3,4}，{4,4,4,3}组合为D₁,D₂模块。

若{1,3,3,4}与{3,3,3,4}组合为D₁模块，则c₅的色集合只能是{4,2,3,1}，故顶点b₆的色集合需要出现颜色1一次，颜色3一次且满足V条件，但剩余的两个集合都不满足。故{1,3,3,4}无法与{3,3,3,4}组合为D₁模块。则剩余的3个含颜色“3”的4-子集必可与{3,3,3,4}组合为D₁模块。

若{1,3,4,4}与{3,3,3,4}组合为D₁模块，则c₅的色集合只能是{4,2,3,1}，故顶点b₆的色集合需要出现颜色1一次，颜色3一次且满足V条件，但剩余的两个集合都不满足。故{1,3,4,4}无法与{3,3,3,4}组合为D₁模块。

故在情形1.5中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.6 包含1个A类模块，3个B类模块，1个C类模块，1个D类模块

若N₆包含1个A类模块，不妨设1个A模块的色集合{1311,1211,1411,1312}。{2,2,2,1}与{2,2,2,3}与两个第二类4-子集组合为B₁模块，{3,3,3,1}与{3,3,3,2}与两个第二类4-子集组合为B₂模块，{4,4,4,1}与{4,4,4,2}与两个第二类4-子集组合为B₃模块，{3,3,3,4}与{4,4,4,3}与两个第二类4-子集组合为C模块，{2,2,2,4}与三个第二类4-子集组合为D模块。

若C模块的色集合为{3433,3134,3234,4344}，则B₂模块没有{2,3,3,4}或{1,3,3,4}，无法组合。

若C模块的色集合为{3433,3144,3244,4344}，则B₃模块没有{2,3,4,4}或{1,3,4,4}，无法组合。

C模块的色集合有且仅有这两种，故在情形1.6中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.7 包含1个A类模块，2个B类模块，2个C类模块，1个D类模块

若N₆包含1个A类模块，不妨设1个A模块的色集合{1311,1211,1411,1312}。{3,3,3,1}与{3,3,3,4}与两个第二类4-子集组合为B₁模块，{4,4,4,1}与{4,4,4,3}与两个第二类4-子集组合为B₂模块，{2,2,2,3}与{3,3,3,2}与两个第二类4-子集组合为C₁模块，{2,2,2,4}与{4,4,4,2}与两个第二类4-子集组合为C₂模块，{2,2,2,1}与三个第二类4-子集组合为D模块。

若C₁模块的色集合为{2322,2123,2423,3233}，则C₂模块的色集合只能为{2422,2144,2344,4244}，则B₂模块没有{1,1,4,4}或{2,3,4,4}，无法组合。

若C₁模块的色集合为{2322,2133,2433,3233}，则C₂模块的色集合只能为{2422,2124,2324,4244}。

若B₁模块的色集合为{3133,3234,3433,4134}，则B₂模块的色集合只能为{4344,4241,4144,1341}。故{1,2,2,3}，{1,1,2,4}，{1,2,3,4}必能与{2,2,2,1}组合为D模块。若{1,1,2,4}必能与{2,2,2,1}组合为D模块，且c₅的色集合是{1,3,2,4}，故顶点b₆的色集合需要出现颜色2一次，颜色4一次且满足V条件，{1,2,2,3}不满足。若{1,1,2,4}必能与{2,2,2,1}组合为D模块，且c₅的色集合是{1,3,2,2}，故顶点b₆的色集合需要出现颜色2两次，{1,2,3,4}不满足。故{1,2,2,3}，{1,1,2,4}，{1,2,3,4}无法与{2,2,2,1}组合为D模块。

若B₁模块的色集合为{3133,3234,3433,4133}，若B₂模块的色集合为{4344,4241,4144,1341}，则同上。若B₂模块的色集合为{4344,4241,4144,1344}，余下的子集为{1,2,2,3}，{1,1,2,4}，{1,1,3,4}必能与{2,2,2,1}组合为D模块，但{1,1,3,4}无颜色2。

C₁模块的色集合有且仅有这两种，故在情形1.7中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.8 包含1个A类模块，3个B类模块，2个D类模块

若N₆包含1个A类模块，不妨设1个A模块的色集合{1311,1211,1411,h}。h为{1,1,2,3}或{1,1,2,4}或{1,1,3,4}。{2,2,2,1}与{2,2,2,3}与两个第二类4-子集组合为B₁模块，{3,3,3,1}与{3,3,3,2}与两个第二类4-子集组合为B₂模块，{4,4,4,1}与{4,4,4,2}与两个第二类4-子集组合为B₃模块，{2,2,2,4}，{3,3,3,4}，{4,4,4,3}的其中两个与两个第二类4-子集组合为D₁，D₂模块。

若B₁模块的色集合为{2122,2423,2322,3123}，B₂模块的色集合为{3133,3432,3233,2132}，B₃模块的色集合为{4144,4342,4244,2142}。剩余的4-子集中只有{1,1,2,4}，{1,2,4,4}，{1,2,3,4}含颜色2，但{1,1,2,4}与{2,2,2,4}无法组合为D模块(与V条件矛盾)，故D模块的色集合不包含{2,2,2,4}。同样{1,1,3,4}与{3,3,3,4}，{4,4,4,3}都无法组合为D模块(与V条件矛盾)。

若B₁模块的色集合为{2122,2423,2322,3123}，B₂模块的色集合为{3233,3431,3133,1231}，B₃模块的色集合为{4144,4342,4244,2142}。因{1,1,2,4}与{2,2,2,4}无法组合为D模块(与V条件矛盾)，则剩余的4-子集中只有{1,2,2,3}，{1,2,4,4}，{2,3,3,4}，{1,2,3,4}含颜色2。若{1,2,4,4}为a₅的色集合，则c₅的色集合是{4,3,2,1}，故顶点b₆的色集合需要出现颜色1一次，颜色2一次且满足V条件，余下4-子集不满足。故D模块的色集合不包含{2,2,2,4}。同样{1,1,3,4}与{3,3,3,4}，{4,4,4,3}都无法组合为D模块(与V条件矛盾)。{1,3,4,4}，{2,3,3,4}，{1,2,3,4}必与{4,4,4,3}组合为D模块，故{1,3,4,4}为a₅的色集合，则c₅的色集合是{3,2,4,3}，故顶点b₆的色集合{3,1,4,2}。因此{1,2,2,3}，{1,1,2,4}，{1,2,4,4}必与{3,3,3,4}组合为D模块，但{1,1,2,4}，{1,2,4,4}无颜色3。

若B₁模块的色集合为{2122,2423,2322,3123}，B₂模块的色集合为{3133,3432,3233,2132}，B₃模块的色集合为{4244,4341,4144,1241}。因{1,1,3,4}与{3,3,3,4}，{4,4,4,3}都无法组合为D模块(与V条件矛盾)。剩余的4-子集中只有{1,3,3,4}，{2,3,4,4}，{1,2,3,4}含颜色3，可与{3,3,3,4}组合为D模块。故{1,3,3,4}为a₅的色集合，则c₅的色集合是{4,2,3,4}，故顶点b₆的色集合{4,1,3,2}。且{1,1,3,4}不含颜色2，因{1,2,2,4}，{1,2,4,4}可与{4,4,4,3}组合为D模块，但第二类4-子集个数不足。

若B₁模块的色集合为{2122,2423,2322,3123}，B₂模块的色集合为{3233,3431,3133,1231}，B₃模块的色集合为{4244,4341,4144,1241}。剩余的4-子集中只有{1,2,2,3}，{2,3,3,4}，{2,3,4,4}，{1,2,3,4}含颜色3，可与{3,3,3,4}组合为D模块。若{1,2,2,3}为a₅的色集合，则c₅的色集合需要出现颜色2一次，颜色3一次且满足V条件，余下4-子集不满足。若{2,3,3,4}为a₅的色集合，则c₅的色集合{3,2,4,3}，则d₅的色集合需要出现颜色2一次，颜色3一次且满足V条件，余下4-子集不满足。故D模块的色集合不包含{3,3,3,4}。剩余的4-子集中只有{1,2,2,4}，{1,2,4,4}，{2,3,3,4}，{2,3,4,4}，{1,2,3,4}含颜色4，可与{4,4,4,3}组合为D模块。若{1,2,2,4}为a₅的色集合，则c₅的色集合需要出现颜色2一次，颜色4一次且满足V条件，余下4-子集不满足。若{2,3,3,4}为a₅的色集合，且c₅的色集合{3,1,4,2}，则d₅的色集合需要出现颜色2一次，颜色4一次且满足V条件，余下4-子集不满足；若{2,3,3,4}为a₅的色集合，且c₅的色集合{3,2,4,3}，则d₅的色集合需要出现颜色3一次，颜色4一次且满足V条件，余下4-子集不满足。因此{1,2,4,4}，{2,3,4,4}，{1,2,3,4}必能与{4,4,4,3}组合为D模块。则D₁模块的色集合为{2144,4234,4344,3142}。剩余的4-子集{1,2,2,3}，{1,2,2,4}，{2,3,3,4}必能与{2,2,2,4}组合为D模块。但{2,3,3,4}无法与{2,2,2,4}组合为D模块(与V条件矛盾)。

当B₁模块的色集合为其他4-子集组合时同理。故在情形1。8中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

在只包含一个A类模块，分配其他三类模块的前提下，其余情形皆为第二类4-子集个数不足以满足，故省去。

情形1.9 包含6个C类模块

若N₆包含6个C类模块，只能{1,1,1,2}与{2,2,2,1}与两个第二类4-子集组合为C₁模块，{1,1,1,3}与{3,3,3,1}与两个第二类4-子集组合为C₂模块，{1,1,1,4}与{4,4,4,1}与两个第二类4-子集组合为C₃模块，{2,2,2,3}与{3,3,3,2}与两个第二类4-子集组合为C₄模块，{2,2,2,4}与{4,4,4,2}与两个第二类4-子集组合为C₅模块，{3,3,3,4}与{4,4,4,3}与两个第二类4-子集组合为C₆模块。

若C₁模块色集合{1211,1312,1412,2122}，C₂模块色集合只能是{1311,1233,1433,3133}，C₃模块色集合只能是{1411,1244,1344,4144}，C₄模块色集合只能是{2322,2123,2423,3233}，但C₅模块色集合需4-子集{2,2,3,4}或{1,2,4,4}，上述两个子集都已使用，故无法组合为C₅模块。

若C₁模块色集合{1211,1322,1422,2122}同理。故在情形1.9中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.10 包含5个C类模块，1个D类模块

若N₆包含5个C类模块，只能{1,1,1,2}与{2,2,2,1}与两个第二类4-子集组合为C₁模块，{1,1,1,3}与{3,3,3,1}与两个第二类4-子集组合为C₂模块，{1,1,1,4}与{4,4,4,1}与两个第二类4-子集组合为C₃模块，{2,2,2,3}与{3,3,3,2}与两个第二类4-子集组合为C₄模块，{2,2,2,4}与{4,4,4,2}与两个第二类4-子集组合为C₅模块，{3,3,3,4}，{4,4,4,3}其中一个与两个第二类4-子集组合为D模块。

同情形1.9，故在情形1.10中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.11 包含2个B类模块，4个C类模块

若N₆包含4个C类模块，只能{1,1,1,2}与{2,2,2,1}与两个第二类4-子集组合为C₁模块，{1,1,1,3}与{3,3,3,1}与两个第二类4-子集组合为C₂模块，{1,1,1,4}与{4,4,4,1}与两个第二类4-子集组合为C₃模块，{2,2,2,3}与{3,3,3,2}与两个第二类4-子集组合为C₄模块，{4,4,4,2}，{4,4,4,3}与两个第二类4-子集组合为B₁模块，但{3,3,3,4}，{2,2,2,4}无法与两个第二类4-子集组合为B₂模块。(不满足B模块的组合条件)

故在情形1.11中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.12 包含1个B类模块，4个C类模块，1个D类模块

若N₆包含4个C类模块，只能{1,1,1,2}与{2,2,2,1}与两个第二类4-子集组合为C₁模块，{1,1,1,3}与{3,3,3,1}与两个第二类4-子集组合为C₂模块，{1,1,1,4}与{4,4,4,1}与两个第二类4-子集组合为C₃模块，{2,2,2,3}与{3,3,3,2}与两个第二类4-子集组合为C₄模块，{4,4,4,2}，{4,4,4,3}与两个第二类4-子集组合为B模块，{3,3,3,4}与{2,2,2,4}分别与两个第二类4-子集组合为D₁,D₂模块。(不满足B模块的组合条件)

若C₁模块色集合{1211,1312,1412,2122}，C₂模块色集合只能是{1311,1233,1433,3133}，C₃模块色集合只能是{1411,1244,1344,4144}，C₄模块色集合只能是{2322,2123,2423,3233}，但B模块色集合需4-子集{1,2,4,4}或{1,3,4,4}，上述两个子集都已使用，故无法组合为B模块。

若C₁模块色集合{1211,1322,1422,2122}，若C₂模块色集合是{1311,1213,1413,3133}，C₃模块色集合只能是{1411,1244,1344,4144}，C₄模块色集合只能是{2322,2133,2433,3233}，但B模块色集合需4-子集{1,2,4,4}或{1,3,4,4}，上述两个子集都已使用，故无法组合为B模块。若C₂模块色集合是{1311,1233,1433,3133}且C₃模块色集合是{1411,1214,1314,4144}，但C₄模块色集合需4-子集{1,2,2,3}或{1,2,3,3}，上述两个子集都已使用，故无法组合为C₄模块。若C₂模块色集合是{1311,1233,1433,3133}且C₃模块色集合是{1411,1244,1344,4144}，但C₄模块色集合需4-子集{1,2,2,3}或{1,2,3,3}，上述两个子集都已使用，故无法组合为C₄模块。

故在情形1.12中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.13 包含2个B类模块，3个C类模块，1个D类模块

若N₆包含3个C类模块，不妨设{1,1,1,2}与{2,2,2,1}与两个第二类4-子集组合为C₁模块，{1,1,1,3}与{3,3,3,1}与两个第二类4-子集组合为C₂模块，{1,1,1,4}与{4,4,4,1}与两个第二类4-子集组合为C₃模块，{2,2,2,3}，{2,2,2,4}；{3,3,3,2}，{3,3,3,4}；{4,4,4,2}，{4,4,4,3}其中取两组与两个第二类4-子集组合为B₁,B₂模块，再从余下的一组中取一个与两个第二类4-子集组合为D模块。

若C₁模块色集合{1211,1322,1422,2122}，若C₂模块色集合是{1311,1213,1413,3133}，C₃模块色集合只能是{1411,1244,1344,4144}，若取{2,2,2,3}，{2,2,2,4}与两个第二类4-子集组合为B₁模块，但B₁模块色集合需4-子集{1,2,2,3}或{1,2,2,4}，上述两个子集都已使用，故无法组合为B₁模块。若取{4,4,4,2},{4,4,4,3}；与两个第二类4-子集组合为B₁模块，但B₁模块色集合需4-子集{1,2,4,4}或{1,3,4,4}，上述两个子集都已使用，故无法组合为B₁模块，则无法组合有两个B模块。

若C₁模块色集合{1211,1322,1422,2122}，若C₂模块色集合是{1311,1213,1413,3133}，C₃模块色集合只能是{1411,1244,1344,4144}，同理，无法组合有两个B模块。若C₂模块色集合是{1311,1233,1433,3133}且C₃模块色集合是{1411,1214,1314,4144},若取{2,2,2,3}，{2,2,2,4}与两个第二类4-子集组合为B₁模块，但B₁模块色集合需4-子集{1,2,2,3}或{1,2,2,4}，上述两个子集都已使用，故无法组合为B₁模块。若取{3,3,3,2},{3,3,3,4}；与两个第二类4-子集组合为B₁模块，但B₁模块色集合需4-子集{1,3,3,4}或{1,2,3,3}，上述两个子集都已使用，故无法组合为B₁模块，则无法组合有两个B模块。若C₂模块色集合是{1311,1233,1433,3133}且C₃模块色集合是{1411,1244,1344,4144}，同理，无法组合有两个B模块。

故在情形1.13中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

情形1.14 包含4个B类模块，1个C类模块，1个D类模块

若N₆包含1个C类模块，不妨设{1,1,1,2}与{2,2,2,1}与两个第二类4-子集组合为C模块，{1,1,1,3}与{1,1,1,4}与两个第二类4-子集组合为B₁模块，{2,2,2,3}与{2,2,2,4}与两个第二类4-子集组合为B₂模块，{3,3,3,1}与{3,3,3,2}与两个第二类4-子集组合为B₃模块，{4,4,4,1}与{4,4,4,2}与两个第二类4-子集组合为B₄模块，{3,3,3,4}，{4,4,4,3}其中取一个与三个第二类4-子集组合为D模块。

若C模块色集合{1211,1312,1412,2122}，B₁模块色集合需4-子集{1,1,2,3}或{1,1,2,4}，上述两个子集都已使用，故无法组合为B₁模块。

若C模块色集合{1211,1322,1422,2122}，B₂模块色集合需4-子集{1,2,2,3}或{1,2,2,4}，上述两个子集都已使用，故无法组合为B₂模块。

故在情形1.14中N₆不存在顶点被多重集点可区别染色的4-E-全染色。

在不包含A类模块，只分配其他三类模块的前提下，其余情形皆因第二类4-子集个数不足以满足情形条件，故省去。

综上所述，当 $\text{2}\le k\le \text{5}$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 4$ ，当k = 6时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)>4$ 。

最后给出当 $\text{2}\le k\le \text{5}$ 时，N_k的点被多重集可区别的4-E-全染色。

先给N₂进行点被多重集可区别的4-E-全染色f₂。f₂ = (1311,1211,1411,1312;2422,2322,2122,2421)。

在N₂的点被多重集可区别的4-E-全染色的基础上，给N₃进行点被多重集可区别的4-E-全染色f₃。f₃ = (1311,1211,1411,1312;2422,2322,2122,2423;3213,1341,3144,1241)。

在N₃的点被多重集可区别的4-E-全染色的基础上，给N₄进行点被多重集可区别的4-E-全染色f₄。f₄ = (1311,1211,1411,1312;2422,2322,2122,2423;3213,1341,3144,1243;3433,3233,3133,3431)。

在N₄的点被多重集可区别的4-E-全染色的基础上，给N₅进行点被多重集可区别的4-E-全染色f₅。f₅ = (1311,1211,1411,1312;2422,2322,2122,2423;3213,1341,3144,1243;3133,3233,3433,3134;4244,4144,4344,4241)。

余{1,2,2,3}，{1,1,2,4}，{1,2,2,4}，{2,3,4,4}，{2,3,3,4}。

通过上述方式就可得出当 $\text{2}\le k\le \text{5}$ 时，N_k的点被多重集可区别的4-E-全染色。

情形2 当 $6\le k\le 12$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)=5$ 。

当 $6\le k\le 13$ ， $\tilde{\eta }\left(N_k\right)=5$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 5$ 。但当k = 13时， $\tilde{\eta }\left(N_k\right)>4$ 。证明与当k = 6时类似，故省去。

当 $6\le k\le 12$ ， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 5$ 。故l = 5时，在N₅的点被多重集可区别的4-E-全染色的基础上，进行如下过程：

[5,4,2,3,3,4;2,1]-S₁型剖分运算，[5,3,4,2;1]-O₃型剖分运算，[3,2,4,3;5]-T₁型剖分运算，[4,3,2,4;5]-T₁型剖分运算，[2,4,3,2;5]-T₁型剖分运算，[1,2,3,4;5,5]-T₂型剖分运算，余{1,1,4,5},{1,4,4,5}。

情形3 当 $13\le k\le 23$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)=6$ 。

当 $14\le k\le 26$ ， $\tilde{\eta }\left(N_k\right)=6$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 6$ 。但当k = 24、25、26时， $\tilde{\eta }\left(N_k\right)>6$ 。证明与当k = 6时类似，故省去。

当 $13\le k\le 23$ ， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 6$ 故l = 6时，在N₁₂的点被多重集可区别的5-E-全染色的基础上，进行如下过程：

[6,4,2,3,4,5;3,1]-S₁型剖分运算，[6,5,3,4,4,5;3,2]-S₁型剖分运算，[6,2,3,5;1]-O₁型剖分运算，[6,4,2,5;1]-O₁型剖分运算，[6,4,5,3;2]-O₃型剖分运算，[4,3,5,4;6]-T₁型剖分运算，[3,5,4,3;6]-T₁型剖分运算，[2,6,1,2;5]-T₁型剖分运算，[1,2,3,4;6,6]-T₂型剖分运算，余{1,1,5,6}，{1,5,5,6}。

情形4 当 $24\le k\le 42$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)=7$ 。

当 $27\le k\le 45$ ， $\tilde{\eta }\left(N_k\right)=7$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 7$ 。但当k = 43、44、45时， $\tilde{\eta }\left(N_k\right)>7$ 。证明与当k = 6时类似，故省去。

当 $24\le k\le 42$ ， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 7$ 。故l = 7时，在N₂₃的点被多重集可区别的6-E-全染色的基础上，进行如下过程：

令i依次为1,2,3进行[7,i + 3,i + 1,i + 2,5,6;4,i]-S₁型剖分运算。

令j依次为1,2令i依次为 $j+\text{1},j+\text{2},\cdots ,3$ 进行[7,i,i + 1,6;j]-O₁型剖分运算，令i依次为1,2进行[7,5,3,6; i] -O₁型剖分运算，[7,5,6,4;3]-O₃型剖分运算。

再进行[5,4,6,5;7]-T₁型剖分运算，[6,5,4,6;7]-T₁型剖分运算，[4,6,5,4;7]-T₁型剖分运算，[2,3,5,6;7,6]-T₂型剖分运算，[1,2,3,4;7,7]-T₂型剖分运算，[7,4,5;1,2,6]-O₄型剖分运算, [7,6,2,3;6,1]-O₅型剖分运算，余{1,1,5,7}。

情形5 当 $43\le k\le 68$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)=8$ 。

当 $46\le k\le 73$ ， $\tilde{\eta }\left(N_k\right)=8$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 8$ 。但当k = 69,70,…,73时， $\tilde{\eta }\left(N_k\right)>8$ 。证明与当k = 6时类似，故省去。

当 $43\le k\le 68$ ， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 8$ 。故l = 8时，在N₄₁的点被多重集可区别的7-E-全染色的基础上，进行如下过程：

令i依次为1,2进行[8,i + 3,i + 1,i + 2,6,7;5,i]-S₁型剖分运算，

令j依次为1,2,3令i依次为 $j+\text{1},j+\text{2},\cdots ,4$ 进行[8,i,i + 1,7;j]-O₁型剖分运算，令i依次为1,2,3进行[8,6,4,7;i]-O₁型剖分运算，之后再进行[8,6,7,5;4]-O₃型剖分运算，[8,4,6;1,2,6]-O₄型剖分运算，[8,2,5,6;3,7]-O₅型剖分运算。

再进行[6,5,7,6;8]-T₁型剖分运算，[7,6,5,7;8]-T₁型剖分运算，[5,7,6,5;8]-T₁型剖分运算，[1,2,3,4;8,8]-T₂型剖分运算，[7,4,5,6,3,2;8]-S₂型剖分运算，

最后 $f_{D_{68}}=\left(7833,3518,3618,8187\right)$ 。

余{1,1,5,8}，{1,1,7,8}，{1,2,5,8}，{1,7,7,8}。

情形6 当 $69\le k\le 110$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)=9$ 。

当 $74\le k\le 112$ ， $\tilde{\eta }\left(N_k\right)=9$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 9$ 。但当k = 111、112时， $\tilde{\eta }\left(N_k\right)>9$ 。证明与当k = 6时类似，故省去。

当 $69\le k\le 110$ ， ${\tilde{\chi }}_{vt}^e\left(N_k\right)\ge 9$ 。故l = 9时，在N₆₈的点被多重集可区别的8-E-全染色的基础上，进行如下过程：

令i依次为1,2,3,4,5进行[9,i+3,i+1,i+2,7,8;6,i]-S₁型剖分运算，

令j依次为1,2,3,4，令i依次为 $j+\text{1},j+\text{2},\cdots ,\text{5}$ 进行[9,i,i+1,8;j]-O₁型剖分运算，令i依次为1,2,3,4，进行[9,7,5,8;i]-O₁型剖分运算，之后再进行[9,7,8,6;5]-O₃型剖分运算，[9,4,5;2,1,6]-O₄型剖分运算，[9,6,7;2,1,8]-O₄型剖分运算，[9,5,7;3,2,7]-O₄型剖分运算，[9,6,7;4,3,8]-O₄型剖分运算，[9,1,5,6;1,8]-O₅型剖分运算，[6,7,4,5;1,2,9,2]-O₆型剖分运算，[5,7,2,3;1,6,9,3]-O₆型剖分运算， [6,8,5,7;2,4,9,2]-O₆型剖分运算。

再进行[7,6,8,7;9]-T₁型剖分运算，[8,7,6,8;9]-T₁型剖分运算，[6,8,7,6;9]-T₁型剖分运算，[4,2,3,5;8,9]-S₃型剖分运算，

[1,2,3,4;9,9]-T₂型剖分运算，[5,6,7,8;9,9]-T₂型剖分运算。

余{1,1,7,9}，{1,8,8,9}，{1,4,6,9}，{1,4,7,9}。

{1,1,7,9}与情形4所余子集{1,1,5,7}，情形5所余子集{1,1,5,8},{1,1,7,8}组合，可得 $f_{D_{109}}=\left(1517,1718,7911,8511\right)$ ，{1,4,6,9},{1,4,7,9}与情形1所余子集{1,1,4,5},{1,4,4,5}组合，可得 $f_{D_{110}}=\left(5411,1694,1794,4145\right)$ ，最终余{1,8,8,9}。

情形7 当 $111\le k\le 165$ 时， ${\tilde{\chi }}_{vt}^e\left(N_k\right)=10$ 。

当 $111\le k\le 165$ ， $\tilde{\eta }\left(N_k\right)=10$ ，则由命题1， ${\tilde{\chi }}_{vt}^e\left(N_k\right)>10$ 。故l=10时，在N₁₁₀的点被多重集可区别的9-E-全染色的基础上，进行如下过程：

令i依次为1,2,3,4,5,6进行[10,i+3,i+1,i+2,8,9;7,i]-S₁型剖分运算，

令j依次为1,2,3,4,5令i依次为 $j+\text{1},j+\text{2},\cdots ,6$ 进行[10,i,i+1,9;j]-O₁型剖分运算，令i依次为1,2,3,4,5进行[10,8,6,9;i]-O₁型剖分运算，之后再进行[10,8,9,7;6]-O₃型剖分运算，[5,8,7,6;10,1]-O₂型剖分运算，[10,7,8;2,1,9]-O₄型剖分运算，[10,5,6;3,2,7]-O₄型剖分运算，[10,6,8;4,3,8]-O₄型剖分运算，[10,7,8;5,4,9]-O₄型剖分运算，[5,6,7,8;3,1,10,1]-O₆型剖分运算，[7,8,2,4;1,6,10,4]-O₆型剖分运算，[6,8,4,5;2,7,10,4]-O₆型剖分运算，[6,8,7,9;2,3,10,2]-O₆型剖分运算，

再进行[8,7,9,8;10]-T₁型剖分运算，[9,8,7,9;10]-T₁型剖分运算，[7,9,8,7;10]-T₁型剖分运算，[6,9,8,7;10]-T₁型剖分运算，令i依次为1,4进行[i,i+1,i+2,i+3;10,10]-T₂型剖分运算，[10,9,3,5;9,4]-O₅型剖分运算，最后 $f_{D_{160}}=\left(10299,931010,91109,102910\right)$ ， $f_{D_{161}}=\left(91033,37510,38510,101109\right)$ 。

余{3,4,7,10}，{2,5,8,10}，{1,2,4,10}，{1,2,5,10}，{1,5,7,10}，{1,5,8,10}，其中{2,5,8,10}与情形5所余子集{1,2,5,8}，情形6所余子集{1,8,8,9}，情形1所余子集{1,2,2,3}组合，可进行[9,3,5,10;1]-O₃型剖分运算，{1,2,4,10}，{1,2,5,10}与情形1所余子集{1,1,2,4}，{1,2,2,4}组合，可进行[2,1,10,5;4]-O₃型剖分运算，{1,5,7,10}，{1,5,8,10}与情形1所余子集{1,1,5,6}，{1,5,5,6}组合，可进行[5,1,7,8;10,6]-O₅型剖分运算。余{3,4,7,10}，{2,3,4,4}，{2,3,3,4}，{1,7,7,8}。

将情形7的 $f_{D_{32}}=\left(1755,5617,5317,7571\right)$ 重新与{1,7,7,8}组合，成为 $f_{D_{32}}=\left(1577,7817,7615,7155\right)$ ，并将 $f_{D_{31}}=\left(1733,3417,3617,7371\right)$ 与余出的{1,3,5,7}重新组合为 $f_{D_{31}}=\left(1733,3517,3617,7371\right)$ , 其中 $f_{D_{31}}$ 可直接通过剖分加入N_k，此时余出子集{1,3,4,7}。将 $f_{D_6}=\left(1511,1251,1351,1415,5122,2315,2415,5251\right)$ 拆为 $f_{D_6}=\left(1511,1251,1351,1415\right)$ 、 $f_{D_7}=\left(1522,2315,2145,5251\right)$ ，其中 $f_{D_7}$ 可直接通过剖分加入N_k，再将 $f_{D_{32}}$ 与 $f_{D_6}$ 颜色“5”的边连在一起，此时两个钻石的左右连接边颜色都为“1”，可剖分进N_k的颜色为“1”边，由此余出子集{1,3,4,7}。则{3,4,7,10}，{1,3,4,7}与情形1所余子集{2,3,4,4}，{2,3,3,4}组合，可进行[3,4,1,10;7,2]-O₅型剖分运算。

因此， $N_k\left(\text{2}\le k\le \text{165}\right)$ 存在点被多重集可区别的l-E-全染色。

4. 结语

根据反证法得到了 $N_k\left(\text{2}\le k\le \text{165}\right)$ 不存在点被多重集可区别的(l-1)-E-全染色，因此 $N_k\left(\text{2}\le k\le \text{165}\right)$ 存在点被多重集可区别的l-E-全染色。并且利用具体构造染色的方法将 $N_k\left(\text{2}\le k\le \text{165}\right)$ 存在点被多重集可区别的l-E-全染色具体给出。之后，可继续利用反证法，用具体构造染色的方法对k ≥ 166进行讨论，并给出相应的染色数。