1. 引言
随着我国社会经济和城市化进程的加速发展,城市居民的生活水平显著提升,从而导致机动车保有量逐年增长,据公安部统计 [1] ,2022年全国机动车保有量达4.17亿辆。现有的道路交通设施所提供的交通容量已经不能满足当前的交通流量需求,城市道路交通拥挤现象愈发严重,道路交通安全、环境污染、能源大量消耗等问题频发,影响着社会经济的健康发展。交通流预测技术利用现有的交通数据,能对未来的交通流量进行实时、精准的预测,有效缓解当前所面临的城市道路拥堵问题。同时,由于交通流受到时空变化和其他干扰因素的影响,表现出强烈的随机性和不确定性,所以当前交通流预测主要以短时交通流预测为主(预测时间跨度通常不超过15 min)。
1994年,Hobeika等 [2] 将ARIMA模型(差分整合移动平均自回归预测模型)应用到高速公路交通流量预测中。交通流数据具有明显的时间相关性,ARIMA模型针对短时交通流时间序列进行建模,能有效的进行短时交通流预测研究,成为了短时交通量预测研究领域的经典模型。2017年,Xu等 [3] 提出了一种基于ARIMA和卡尔曼滤波器的实时道路交通状态预测算法,实验证明基于ARIMA和卡尔曼滤波的实时道路交通状态预测可行且准确率更高。2018年,王晓全等 [4] 提出一种组合模型ARIMA-GARCH-M进行短时交通流预测,并利用城市快速路交通流数据进行模型预测精度的检验,结果表明:ARIMA-GARCH-M模型相比于ARIMA-SVR模型和ARIMA-GARCH模型的预测结果,该组合模型具有较好的预测效果。2019年,刘学刚等 [5] 考虑道路交通流时间序列的非平稳性特征,通过差分使数据变得平稳,构建ARIMA(6,1,6)模型进行短时交通流进行预测,结果表明:ARIMA模型可以很好地拟合短时交通量数据,在短时交通量预测中有很大应用价值。2020年,张腾飞等 [6] 在考虑历史数据较少的基础上,通过建立ARIMA模型进行短时交通量的静态预测,避免多步预测误差递增的问题,结果表明:所建立的ARIMA 模型可以较好地对短时交通量进行短时预测;2022年,张玺君等 [7] 提出一种基于SARIMA-GA-Elman的组合预测模型来处理单一模型在交通流特征挖掘和神经网络模型收敛速度上存在的缺陷,实验表明,该模型相较于单一模型展现出了良好的预测精度和鲁棒性。上述研究表明,ARIMA模型能将非平稳的时间序列转化为更为平稳的时间序列,从而能够达到更好的预测效果。同时,随着交通流预测领域对ARIMA模型研究的深入,国内外学者对于如何提升ARIMA模型的预测可靠性方面也展开了广泛的研究,此类模型的预测精度已经得到了较好的提高。但是如何提高此类模型预测结果的可靠性仍需展开进一步研究。
针对如何提升ARIMA模型预测可靠性问题,本文提出基于新型数据分解的ARIMA模型短时交通量预测模型,利用该数据分解方法对原始交通流序列信号进行分解,以期提高ARIMA模型的预测精度,并将本文模型的预测结果与其他传统短时交通量预测模型预测结果进行比较,评估本文模型的性能。
2. 基于数据分解方法和ARIMA模型的短时交通流预测方法
2.1. 数据分解方法
2.1.1. 时变滤波经验模态分解
经验模态分解(Empirical Mode Decomposition, EMD)方法是一种时频域信号处理方法,对非线性、非平稳信号的处理具有良好的效果 [8] 。EMD将原始序列信号
分解为多个不同的本征模态函数(Intrinsic Mode Function, IMF)
和残余分量
之和:
(2.1)
虽然EMD方法在理论上取得了优异的成果,但在算法的实际应用上存在着模态混叠、迭代次数过多、缺乏停止迭代的标准等缺陷 [9] 。
时变滤波经验模态分解(TVF-EMD)方法2017年由Li等 [10] 提出,对经验模态分解方法存在的缺陷进行了改进。TVF-EMD将输入信号分解为一系列局部窄带分量过滤,利用Hilbert谱的局域窄带信号(局部窄带信号)来代替本征模态函数作为迭代停止条件,达到有效缓解模态混叠现象的目的,能更好地消减数据中存在的非线性、非平稳成分,提高数据的质量。该方法的基本思想是为确定局部截止频率,对信号进行时变滤波处理 [10] ,具体分解操作为:
1) 利用Hilbert变换计算径流序列
的瞬时幅值
和瞬时频率
:
(2.2)
(2.3)
式中,
为径流序列
的Hilbert变换。
2) 确定瞬时幅值
的局部极大值序列和局部极小值序列,分别表示为
和
;
3) 对
进行插值得到
,以同样的方法对
得到
,计算瞬时均值
和瞬时包络
:
(2.4)
(2.5)
4) 分别对
和
进行插值,得到
和
并计算瞬时频率分量
和
:
(2.6)
(2.7)
5) 计算局部截止频率
:
(2.8)
6) 为解决间歇问题,重新对局部截止频率
进行调整;
7) 计算信号
,并将
的极值点作为构造时变滤波的节点,采用B样条插值对径流序列
进行逼近;
8) 计算停止准则
,如果
,则可以确定
的局部窄带信号,不满足则令
,重复执行(1)~(8)步骤:
(2.9)
式中,
为两分量信号的Loughlin瞬时带宽;
为单个分量瞬时频率的加权平均值;
为瞬时包络局部平均值。分解后得到所有的子序列之和为原径流序列
的值。
2.1.2. 数据分解方法对比
由于EMD具有模态混叠现象,分解出IMF的过程中需要迭代很多次,而停止迭代的条件缺乏一个标准,会出现分解过度或者分解不彻底的问题;变分模态分解(Variational Mode Decomposition, VMD) [10] 方法通过自适应分解,有效地避免了模态混叠问题,实现了分量的准确分离,但VMD方法中高频的信号分离上能力较弱;TVF-EMD作为EMD方法的升级,通过收敛准则,自适应分解层数,利用局部窄带信号代替本征模态函数,有效地改善了EMD分解方法中存在的弊端、提高了分离能力。所以本文选取TVF-EMD方法进行应用分析。
2.2. ARIMA模型介绍
ARIMA(p,d,q)模型由自回归模型(Auto Regression, AR)、移动平均模型(MA, Moving Average)和差分整合方法(I, I-for Integrated)三部分组成 [11] ,其中d是需要对数据进行差分的阶数。ARIMA基本原理是将非平稳时间序列转化为平稳时间序列然后将因变量仅对它的滞后值和随机误差项的现值进行回归 [4] ,其公式定义为:
(2.10)
式中,
,
分别为预测值和历史交通流数据;
为常数项;
,
分别为自相关系数和误差项系数;p,q分别为自回归阶数和移动平均阶数;
,
分别为模型的误差和时间点i的偏差。
在建立ARIMA(p,d,q)模型前,需要将数据平稳化,即需要对数据进行差分处理,差分的阶数d一般选择一阶或者二阶,通过假设检验(Augmented Dickey-Fuller test, ADF)判断序列是否存在单位根来确定序列的平稳性。对于平稳时间序列模型p和q阶数的确定,本文采用赤池信息准则(Akaike Information Criterion, AIC) [12] 对模型进行定阶,准则定义如下:
(2.11)
式中,k表示模型的参数数量;L为似然函数。
2.3. TVF-EMD-ARIMA模型的建立
笔者根据TVF-EMD方法能有效处理具有非平稳和非线性特点的短时交通量数据,提出TVF-EMD方法与ARIMA模型相结合的短时交通量预测模型(TVF-EMD-ARIMA),预测模型的具体步骤如下所示:
步骤一:将选取的短时交通量数据经过TVF-EMD分解得到多个具有不同特性的窄带子序列
,
,进一步对更为平稳的子序列展开建模分析;
步骤二:将实验数据分为测试集和训练集,分别进行模型的建立和性能评估;
步骤三:对分解得到的各分量建立ARIMA模型:采用ADF对模型进行平稳性检验,确定差分阶数d,采用BIC对各分量ARIMA(p,q)模型进行定阶;
步骤四:计算模型中的残差统计值,如果不合适则针对残差进行白噪声检验,当残差统计值合适时开始预测;各分量预测结果叠加得到最终的预测值。图为预测模型流程图1。
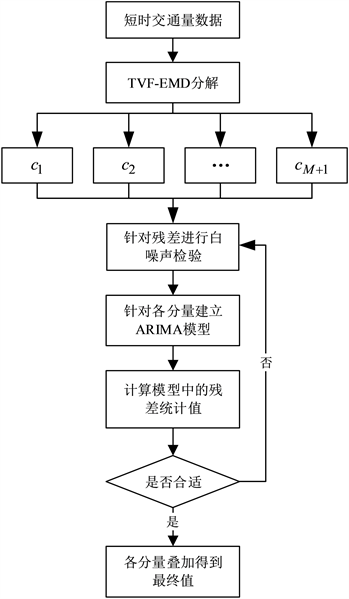
Figure 1. Flow chart of TVF-EMD-ARIMA
图1. TVF-EMD-ARIMA模型流程图
3. 案例应用分析
3.1. 数据说明
短时交通量数据来源于重庆市某主干道的路口,数据统计间隔为5 min。通过数据预处理方法对错误数据与丢失数据进行修复;之后进行数据集的划分,利用留出法划分为互斥的两部分,一部分作为训练集,一部分作为测试集,通常情况下将大约2/3~4/5的样本用于训练,所以本文选取前2/3的数据对模型进行训练,剩余1/3的数据进行测试,原始时间序列如图2。
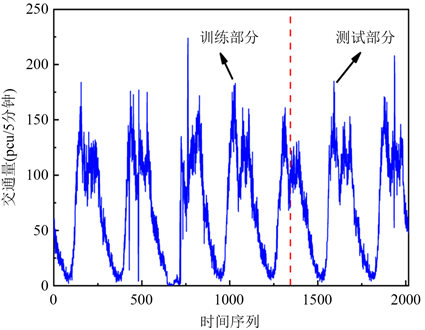
Figure 2. Time series of short-term traffic volume
图2. 短时交通量时间序列
3.2. 评价准则
为了更好地评估TVF-EMD-ARIMA模型的预测效果,笔者选取平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)作为本文的评价指标,MAE、MAPE、RMSE越小,预测误差越小。
其计算式如下式所示:
(3.1)
(3.2)
(3.3)
3.3. 案例应用
本文运用TVF-EMD对短时交通量数据进行信号分解处理,得到8个子序列,如图3。分别对8个子序列建立ARIMA模型进行预测。针对各子序列利用赤池信息准则分别确定模型阶数,各自序列的ARIMA模型均为ARIMA(1,1,1)。对于带宽阈值
和B样条阶数l,设定
,
。
为证明新建模型TVF-EMD-ARIMA的优势,笔者选取3种模型进行对比,分别为ARIMA、EMD-ARIMA和VMD-ARIMA。ARIMA模型能有效处理线性特征的数据,具有模型简单、训练时间短等优点;EMD-ARIMA模型和VMD-ARIMA是基于数据分解方法的混合预测模型,将EMD-ARIMA和VME-ARIMA与TVF-EMD-ARIMA模型进行对比,能进一步分析本文模型的有效性。这3种不同模型的评价指标结果如表1,预测结果如图4。
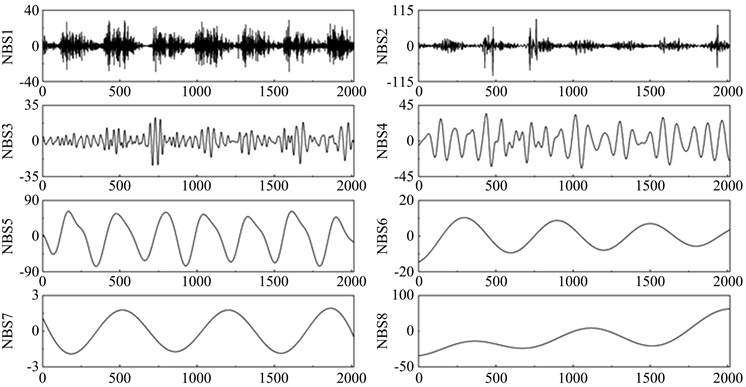
Figure 3. Decomposition results of TVF-EMD
图3. TVF-EMD分解结果
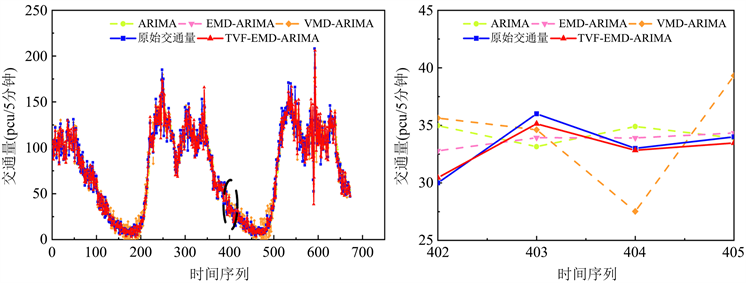
Figure 4. Prediction results of different prediction methods
图4. 不同预测方法预测结果

Table 1. Comparative analysis of prediction accuracy of different methods
表1. 不同方法预测精度对比分析
3.4. 预测结果分析
1) 由图4和表1可以看出,TVF-EMD-ARIMA模型的拟合效果优良;本文采用的3个评价指标分别为MAE = 5.4728,MAPE = 0.0931,RMSE = 7.7118。与对比EMD-ARIMA模型相比,3项评价指标分别相差1.1508、0.0273、1.4184。评价结果表明:TVF-EMD-ARIMA模型采用新型数据分解方法,利用时变滤波技术,对非线性和非平稳信号进行分析,对噪声干扰具有一定的鲁棒性,有效解决了EMD-ARIMA模型中存在的模态混叠问题,提升了预测精度;同时,与VMD-ARIMA模型相比,TVF-EMD-ARIMA模型性能上也显示出一定的优越性。
2) ARIMA模型的3个评价指标结果分别为MAE = 9.1428、MAPE = 0.1706、RMSE = 13.0657。与TVF-EMD-ARIMA相比,具有明显的指标差距,差距分别为3.6700、0.0775、5.3539。本案例所使用的是非线性数据,结果表明ARIMA模型在非线性数据上的应用能力较差,预测精度较低。
4. 结论
本文提出一种基于TVF-EMD方法的ARIMA模型。实验结果表明,TVF-EMD-ARIMA模型能有效提升单一ARIMA模型的预测精度,相较于EMD-ARIMA模型和VMD-ARIMA模型相比预测性能也得到了有效的提升,为短时交通流预测提供了一种新的预测方法。然而,上述方法仅能够提供准确地预测结果,无法考虑短时交通流数据中不确定因素的影响。为此,有必要展开短时交通流概率预测研究,进而为后续风险评估提供理论指导。
基金项目
全国大学生创新创业训练项目,项目编号:S202210618039;S202210618027。
NOTES
*通讯作者。