1. 引言
智能反射表面(Intelligent Reflecting Surface)被认为是第六代(6G)网络的关键技术之一,可以通过软件控制反射元件参数来实现智能和可编程的无线传播环境,从而改善基站(Base Station, BS)和用户之间的无线信道并且增强系统性能 [1] [2] [3] 。通常,IRS由大量的无源反射元件组成,可以通过调整每个反射元件的反射参数(幅度和相位)来改变入射信号的反射。在毫米波大规模MIMO系统中,由于毫米波的传输特性,其遇到障碍物阻挡时,信号的视距(Line Of Sight, LOS)传播会受到严重影响,IRS被引入系统来建立新的稳定的视距连接 [4] 。为了充分发挥IRS的优势,研究需要精确的信道状态信息(Channel Station Information, CSI)来进行设计。因此,实现IRS辅助通信系统的一个重要任务是进行信道估计。与传统系统中的信道估计不同,IRS通常是由无源设备构成,无源中继不能接收导频信号,只能估计用户到IRS再到BS的级联信道。对于采用传统方法(例如最小二乘法(LS)方法 [5] 和线性最小均方误差(LMMSE)方法 [6] )估计上行链路的级联信道,然而级联通道通常具有较大的尺寸,这些方法会产生大量的训练开销并且计算复杂度较高。在文献 [7] 中,通过利用BS至IRS和IRS至用户之间信道的低秩结构,开发了一种基于稀疏矩阵分解的信道估计方法。该方法需要每次关闭一些无源元件。然而对每个IRS元件进行单独的振幅控制,实施ON/OFF开关的成本较大 [8] 。文献 [5] 中设计了一种二进制反射控制LS信道估计方案,其中IRS在每个时隙仅打开一个反射元件并关闭其余反射元件。虽然BS没有接收到来自其他反射元件的任何干扰,但其只能获得用于信道估计的信噪比(Signal to Interference plus Noise Ratio, SNR)。
与传统方法相比,深度学习(Deep Learning, DL)技术可以帮助更好地提取输入输出信号的固有关系,并实现更可靠的信道估计,如OFDM系统 [9] 和大规模MIMO系统 [10] 。文献 [11] 基于IRS辅助的大规模MIMO系统,提出了两个相同的卷积神经网络(CNN),用于以顺序方式估计视距信道和级联信道。然而,由于估计的直接信道被用于构造估计的级联信道,因此会有误差传播问题。A. Taha等提出的混合无源/有源IRS对于信道估计,在文献 [12] 和 [13] 中分别提出了基于压缩感知(Compress Sensing, CS)和DL的信道估计方法,利用角域信道稀疏性来减少导频开销。然而,CS公式中采用的2D离散傅里叶变换(Discrete Fourier Transform, DFT)矩阵由于不可忽视的功率泄漏效应而产生性能损失 [14] ,并且不同子载波之间的结构化信道稀疏性没有得到充分利用。
为了减少导频损耗,降低信道估计难度,研究引入了一种包含有源/无源元件的混合IRS架构。混合IRS架构可看作是有源中继,可以主动接收用户和基站发送的导频信号,与基带连接并进行采样信道估计。考虑到毫米波信道的稀疏特性,研究使用贪婪算法及正交匹配追踪(Generalized Approximate Message Passing, GAMP)从估计的采样信道全部信道。由于毫米波容易受到传播环境的影响,压缩感知重构出的信道是带有噪声的,信道估计问题本质上可以看作是去噪问题 [15] 。信道矩阵含有实部和虚部两个部分,大部分研究都是采取实部虚部分开输入至实数卷积网络分开训练,此类方法通常未考虑到信道实部虚部之间的相关性,容易造成信道信息的部分丢失,降低信道恢复的精确度。为此,研究引入了文献 [16] 的复数卷积层,可以实现将信道矩阵的实部和虚部同时输入复数卷积网络进行训练,用以增强实部虚部的相关性,减少信息丢失,提升信道重构的精确度。同时,为了在不增加网络深度和宽度的前提下扩大深度卷积网络的感受野,研究还引入了空洞卷积层 [17] 。考虑到毫米波信道的稀疏特性,研究引入了注意力机制以加强噪声特征提取性能,恢复出噪声矩阵,通过重构部分恢复出去噪信道矩阵。仿真结果表明,本文所提方法可以利用更少的导频重构出更精确的CSI,有效减少了导频损耗,同时,对于不同路径数量的情况下,网络性能也相对稳定。
2. 模型与问题描述
2.1. 系统模型
IRS正在成为大规模天线系统的低成本绿色替代方案 [18] 。当视距无线传输(Line Of Sight, LOS)传播被阻断时,IRS可以实现重新改变无线环境以帮助发送方和接收方之间的信号传输 [19] 。如图1所示,LOS传输信道被阻挡住,基站发送的信号无法直接传输到用户,通过将IRS布置在基站与用户的周围建筑物上创造非视距传播(Non Line Of Sight, NLOS)传输,发送的信号可以通过IRS元件反射给用户。
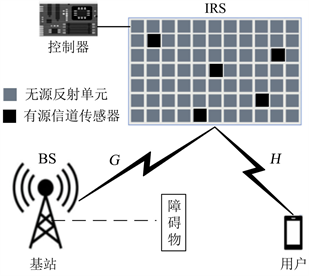
Figure 1. IRS assisted millimeter wave MIMO systems
图1. 智能反射面辅助的毫米波系统
本文研究IRS辅助的毫米波大规模MIMO的单用户下行链路,采用具有K个子载波的正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统,部署IRS以辅助从基站(Base Station, BS)到用户的NLOS信号传输。假设IRS是具有M个反射元件的UPA阵列。BS配备了
个天线。
表示从BS到IRS的信道,
表示从IRS到用户的信道。IRS的每个反射元件可以通过智能控制器设置重构相移和振幅。IRS包含有源元件和无源元件,其有源反射单元有两种工作模式:1) 信道感知功能:可以主动接收信号进行信道估计并与基带连接;2) 反射功能:对信号进行反射传输。无源反射单元仅具备反射功能 [13] 。
2.2. 信道模型
假设BS端和用户端的天线阵列均采用均匀线性阵列(ULA),IRS端的天线阵列采用均匀平面阵列(UPA)。
对于BS端至IRS端的信道,G有:
(1)
(2)
(3)
(4)
(5)
其中,L为发射端到IRS端的路径数,
为与路径相关的复增益,
为IRS端接收阵列的归一化响应向量,
为BS端发射阵列的归一化响应向量,
和
为第l条路径到达角的方位角和仰角。
为第l条路径的偏离角。
IRS的反射系数矩阵为:
(6)
其中,
表示第m个反射元素的相移,
为反射面元件的反射幅度,为了方便设计通常设置为
。
IRS至用户的信道表示为:
(7)
(8)
(9)
(10)
其中,
是离散延迟域中的毫米波MIMO离散信道脉冲响应,可以将其建模为几何信道模型 [20] 。L为IRS端到用户的路径数,
为与路径相关的复用增益,
为采样周期,g为脉冲整形滤波器,
为离散延迟,
和
分别为用户端和IRS端发射阵列的归一化响应向量,
和
为第l条路径到达角的方位角和仰角,
和
为第l条路径的偏离角。
第k个子载波在BS处接收的上行链路信号为:
(11)
用户接收的第k个子载波的第b时隙的信号表示为:
(12)
其中,
表示第k个子载波在第b个时隙发送的导频信号,
为加性高斯白噪声
。
3. 算法设计
3.1. 基于压缩感知的信道估计
研究采用了基于压缩传感(Compress Sensing, CS)的信道估计算法,有效地节约了无线电资源和网络基础设施。为了减少训练开销,本文利用KatriRao和Kronecker乘积,获得毫米波信道的稀疏表示。毫米波信道具有角度域稀疏性,而压缩感知算法对于这种可压缩的稀疏信号,可以使用远低于奈奎斯特的采样频率对信号采样,设计重构算法来恢复信道。如图1所示,IRS中随机分布
个有源反射元件,基站端和用户端可以发射少量导频信号并由IRS的有源元件接收,估计出采样信道,利用压缩感知算法从估计的采样信道重构出全部信道。由于基站和IRS的位置在布置完成之后基本是固定的,基站和IRS之间的信道将在很长一段时间内保持不变,可以直接通过LS算法进行估计,研究重点关注的是用户至IRS之间的可变信道的估计问题。
根据A. Taha [13] ,用户至IRS的信道
可写成:
(13)
其中,
表示路径增益向量,
为阵列响应向量。
将
表示为
,其中:
(14)
(15)
采样信道表示为
:
(16)
其中,
表示有源反射单元在IRS上的布置情况,
表示采样过程中被激活的有源反射单元布置情况,
表示需要求解的稀疏向量即本文需要估计的用户至IRS之间的信道,
表示接收噪声矢量。
信道重构即可变为求解如下非凸问题:
(17)
为了充分利用毫米波信道的稀疏特性,本文采用贪婪算法及正交匹配追踪(Generalized Approximate Message Passing, GAMP)来解决该非凸问题,重构出信道。
3.2. AM-DnCNN网络设计
上文基于压缩感知估计出的信道带有噪声,阻碍了信道恢复的精确度。信道矩阵为复数矩阵,目前大部分基于深度学习估计信道的神经网络都是将实部和虚部分开输入实数值卷积网络进行训练,这种训练方法会导致复数相位信息缺失等问题。受文献 [21] 启发,研究设计了一种引入复数卷积层的注意力引导的深度去噪神经网络(Attention Mechanism-Denoising Convolution Neural Network, AM-DnCNN)网络如图2所示。
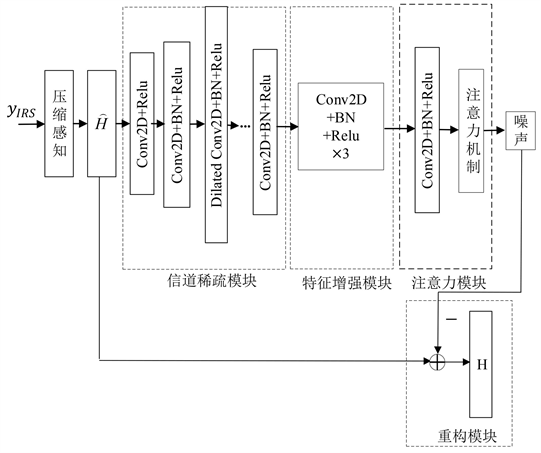
Figure 2. AM-DnCNN Network structure diagram
图2. AM-DnCNN网络结构图
复数卷积层如式(18) (19)所示:
(18)
(19)
其中,W表示复数卷积网络的复数权重,H表示输入的含有噪声的信道矩阵数据。
AM-DnCNN网络的输入为上一节介绍的基于压缩感知算法估计的带有噪声的信道,由于注意力机制和深度卷积网络在特征提取和去噪方面的突出性能,研究提出的AM-DnCNN网络可以进一步提高信道估计精度。本文所提网络可以分为四个部分,即信道稀疏特征提取(Channel Sparse Feature Extraction, CSFE)部分、信道特征增强 (Channel Feature Enhancement, CFE)部分、注意力机制(Attentional Mechanism, AM)部分和信道重构(Channel Reconstruction, CR)部分,网络可以从噪声观测中学习噪声,从而重构出去噪信道。下文详细的介绍了四个模块的基本构成和实现功能。
1) CSFE:
神经网络通常采用两种方法来扩大感受野,一是增加网络深度,二是增加网络宽度。然而,加深网络深度会加大训练困难;加大网络宽度会涉及更多的参数增加去噪网络的复杂性。AM-DnCNN网络的CSFE部分用于获得含噪声信道的浅层特征,受文献 [17] 启发,网络引入了空洞卷积,空洞卷积层可以放大接收野,减少网络深度获得更加密集的数据,降低去噪网络的估算成本和内存消耗。CSFE包含空洞卷积层和CNN卷积两种卷积层共12层。卷积核的大小设置为3 × 3,其中空洞卷积层的扩张因子设置为2,空洞卷积层放置在第二、五、九、十二层。每一层卷积层后面都加入归一化层(Batch Normalization, BN),用来加快网络的学习速度,防止过拟合。激活函数采用文献 [21] 所提的CRelu如式(20)所示,更适合复数卷积网络,改善梯度消失的问题。
(20)
2) CFE:
CFE充分利用了网络的全局和局部特征,增强了网络去噪的性能。深层网络的性能会受到浅层削弱作用,如深度增长 [22] [23] 等深度残差网络模型,为了解决该类问题,AM-DnCNN网络加入了特征增强块去噪。在处理给定的包含噪声信道矩阵时与CSFE功能互补。CFE由两种类型组成:Conv2D + BN + CReLU和Conv2D,Conv2D + BN + CReLU安装在13~15层,Conv2D为第16层,卷积核大小为64 × 3 × 3。将提取的特征通过卷积层进行噪声提取,再通过全连接层输出噪声信道矩阵。
3) AP:
复杂的信道会增加训练的难度,AM-DnCNN网络加入了注意力模块来训练去噪模型,用以增强网络在前一阶段学习的噪声特征。AP可分为两个步骤来实现,第一步是获得噪声权重,第二步利用获得的噪声权重对CFE部分输出的噪声矩阵进行加权,以提取更突出的噪声特征,提高网络的去噪效率。
注意力部分可以快速提取关键噪声特征,用于复杂的噪声任务。将CFE部分提取噪声信道矩阵输入到注意力网络中,输出特征权重参数Q与网络前面提取的信道噪声矩阵相乘,得到新的噪声矩阵。注意力机制算法如表1所示。
4) CRP:
将估计的带有噪声的信道输入AM-DnCNN网络进行训练,输出噪声矩阵。将压缩感知估计的信道与噪声矩阵做相减处理,获得去噪矩阵。信道重建块可以用式(21) (22)表示:
(21)
(22)
其中,
为压缩感知算法估计的带有噪声的信道,H为真实信道矩阵,E为实际噪声矩阵,
为网络输出的估计噪声矩阵,
表示为去噪矩阵。
本文采用均方差(Mean Squared Error, MSE)损失函数定义为:
(23)
其中,N为训练样本数量。
AM-DnCNN网络采用归一化均方误差(Normal Mean Square Error, NMSE)来评价信道估计质量。NMSE是用来衡量估计量与被估计量之间差异程度,表达式为:
(24)
其中:
是估计的信道矩阵,NMSE越小,信道估计准确度越高。
4. 实验仿真
4.1. 系统参数设置
实验中,设置BS至IRS的距离为150米,用户在距离IRS 30米处的10米半径圆圈内。路径损耗为
,
为用户至IRS距离。表2给出了系统仿真参数的设置。

Table 2. Parameter settings for massive MIMO system
表2. 大规模MIMO系统的参数设置
4.2. 网络参数设置
利用Matlab仿真信道生成5000个训练样本和1000个测试样本,参数设置如表3所示。
4.3. 性能分析
为了确定深度去噪网络的最佳卷积层数,图3展示了网络的CSFE部分设置不同卷积层数量的性能对比,分别给出了−10 dB,10 dB,20 dB三种不同信噪比的性能对比,可以看出卷积层数在15层左右NMSE性能就趋于收敛,故设置该部分卷积层数为15。
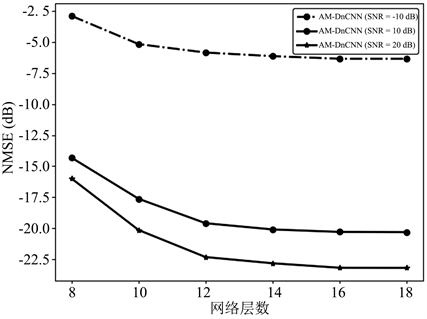
Figure 3. Performance comparison of different network layers
图3. 不同网络层数的性能对比
为了分析不同信噪比情况下的网络去噪性能,图3展示了所提算法与如下3种基线算法的复杂度量级对比,包括:
1) OMP (Block Coordinate Descent, BCD)算法 [24] :将信道估计转换为稀疏信号恢复问题,并通过正交匹配追踪(OMP)算法来解决。
2) Channel Net算法 [25] :采用双卷积神经网络(CNN)结构,将接收到的导频信号输入网络估计信道,未考虑到信道实部虚部的内在联系,容易造成信道信息部分丢失。
3) LS:最小二乘法,信道估计开销较大且计算复杂度较高。
由图4可以看出,与4种基线方法相比,信噪比在范围−10~20 dB时,本文所提AM-DnCNN算法有较明显的性能提升。这是因为本本所提算法考虑到信道实部虚部的内在联系,引入了复数卷积网络和空洞卷积层,减少了信息丢失量,同时引入了注意力引导的深度去噪网络,提高了信道的恢复精度。另外,实验还对比了采用不同信噪比训练的网络的NMSE性能和固定SNR = 10 dB,路径数量为8训练的网络的NMSE性能进行对比,可以看出只有较小的性能变化,由此可以证明本文所提算法针对不同信噪比,同样可以获得较好的NMSE性能,证明该网络具有鲁棒性。

Figure 4. Comparison of NMSE performance under different SNR
图4. 不同信噪比情况下的NMSE性能对比
为了对比不同导频长度下的NMSE性能对比,图5展示了AM-DnCNN与三种基线算法的性能对比。由图5可以看出,随着导频长度的增加,四种算法信道估计的NMSE性能也随之提升,这是因为导频长度的增加代表其含有的信道信息也更多,更有利于进行信道估计。本文所提算法在导频长度为20左右时,NMSE性能就趋于收敛,而其他算法需要超过60的导频长度才能开始收敛。因为本文引入了混合IRS架构,其少量的有源元件可以主动接收导频信号估计信道,所提AM-DnCNN算法仅需要20左右的导频长度就可以获得较好的NMSE性能,而其他方法大概需要超过60的导频长度才能获得较为稳定的NMSE性能。有效减少了导频损耗。
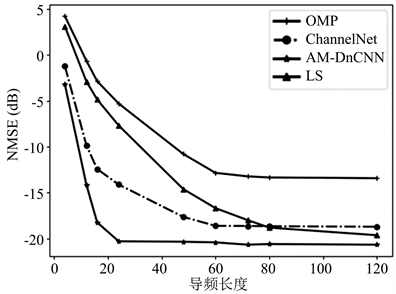
Figure 5. Comparison of NMSE performance at different pilot lengths
图5. 不同导频长度下的NMSE性能对比
为了对比不同路径情况下的性能,图6展示了四种算法在不同路径数量情况下的NMSE性能对比。
由图6可以看出,本文所提AM-DnCNN算法的性能在不同路径数量情况下均优于OMP算法和ChannelNet算法。此实验还对比了基于SNR = 10 dB,路径数量为8训练的AM-DnCNN网络和基于SNR = 10 dB,不同数量路径的网络性能,由图6也可以看出,本文所提算法在不同路径数量情况下也能获得较稳定的NMSE性能,由此可以证明该网络在不同数量路径下也具有鲁棒性。

Figure 6. Comparison of NMSE performance in different paths
图6. 不同路径下的NMSE性能对比
5. 总结
针对无源智能反射面辅助大规模MIMO系统的信道难以进行估计的问题,本文引入了一种包含有源/无源元件的混合智能反射面,并设计了一种基于注意力引导的复数深度卷积网络来提高信道的恢复精度。经过仿真实验,结果表明,本文所提方法在少量激活的有源反射元件的情况下,仅需20左右的导频长度就能获得更加精确的信道状态信息,有效减少了导频损耗。本文所设计的复数深度卷积网络更好的考虑到了信道矩阵实部和虚部之间存在的隐藏关系,可以获得更多的信道信息。同时,本文引入的注意力网络和空洞卷积层,有效提升了网络的去噪性能,更有利于信道恢复精确度的提升。此外,所提网络在不同信噪比和不同数量路径情况下,也能获得较好的NMSE性能,证明了网络具有鲁棒性。
基金项目
华为技术有限公司合作项目(YBN2019115054)资助。