经管类虚拟仿真实验系统学习效果分析——基于AHP-结构熵权法

Analysis of the Learning Effect of Virtual Simulation Experiment System in Management Education: Based on AHP-Structural Entropy Weight Method

摘要: 本文针对已有虚拟仿真系统评价指标体系指标权重确定方法单一的问题，采用层次分析法和结构熵权法分别计算学生和专家的权重，并进行组合赋权。将学生体验与专家意见相结合，给出了更为客观、准确的经管类虚拟仿真实验系统学习效果评价体系及指标权重。通过S大学经济管理学院市场营销虚拟仿真实验平台进行实例检验。研究成果为虚拟仿真实验系统的进一步开发提供了科学参考。

Abstract: Addressing the issue of the single method for determining the weight of the evaluation index sys-tem for existing virtual simulation systems, the Analytic Hierarchy Process (AHP) and Structural Entropy Weight (SEW) methods are used to calculate the weights of students and experts, separately, which are then combined for weighting in this paper. By combining student experiences with expert opinions, a more objective and accurate evaluation system and index weight for learning outcomes of virtual simulation experiments in business management have been proposed. Using the above-mentioned method, an evaluation was conducted on the learning outcomes of the market marketing virtual simulation experimental platform of the School of Economics and Management of S University. The results provide a scientific reference for the further development of virtual simulation experimental systems.

1. 引言

随着国家政策主导与现代化数字技术飞速发展，虚拟仿真实验学习技术已被广泛应用于国内的高校教学 [1] 。在教育部大力推动下，各高校积极响应国家政策，大力发展虚拟仿真实验课程 [2] 。建立客观、准确的虚拟仿真实验系统学习作用评价体系，是提高虚拟仿真实验系统教学效果，建设我国信息化高等教育的重要基础 [3] 。

我国对虚拟仿真学习评价体系的研究尚处初级阶段 [3] 。2011年，杨雪等 [4] 基于反馈理论提出“以学习者为中心”的虚拟仿真实验设计理念，从感官、行为、交流三个层面对学习者表现进行评定。此后，李丽等 [5] 针对汽车电路虚拟仿真实验系统构建评价指标体系，并利用模糊层次分析法确定指标权重。2018年，何聚厚 [6] 采用问卷调查法、文献分析法等建立起全面、完善的虚拟仿真系统学习效果三级评价指标体系，合理解答“如何评价学生在虚拟仿真系统中的学习效果”问题。随后，蒿丽萍 [7] 系统地总结归纳了虚拟仿真实验评价机制。在此基础上，张咪 [8] 着重考虑仿真实验学习中动作技能的考评，基于多元智能理论、学习结果分类理论建立起新的评价指标体系，并利用层次分析法确定权重。

以上研究虽已建立起较为全面、完善的虚拟仿真系统评价指标体系，但确定指标权重方法单一，结果易受主观因素影响。研究表明，虚拟仿真实验系统负责教师大多具有行政职务，年龄较大，开发虚拟仿真实验系统时缺乏对一线年轻教师经验与学生自身体验的考虑 [8] 。

本文总结前人研究成果，提出AHP-结构熵权法进行指标组合赋权。分别对虚拟仿真系统使用学生和开发专家进行问卷发放，利用层次分析法计算使用学生角度权重，利用结构熵权法计算开发专家角度权重，并将两套权重进行组合，得到综合赋权。该方法将领域内专家的优势经验与学生参与虚拟仿真实验的真实体验结合，给出了更为客观、准确的经管类虚拟仿真实验系统学习效果评价体系，为虚拟仿真实验系统的进一步开发提供了科学参考。

2. 经管类虚拟仿真实验系统学习效果评价指标体系建立

本文以现有虚拟仿真(下文简称“虚仿”)实验评价体系为依据 [6] ，根据学生实际使用情况和教师建议进行拓展，共设3个一级指标，9个二级指标，25个三级指标，构建评价体系如图1所示。

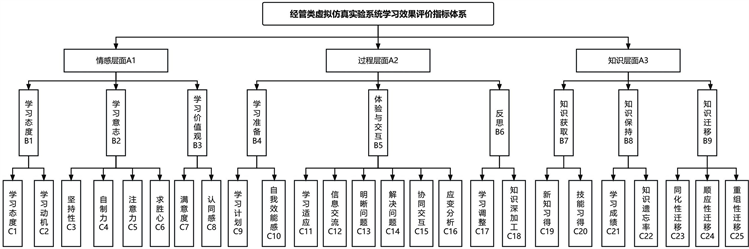
Figure 1. Evaluation Index of learning effect of virtual simulation system for students of economics and management

图1. 经管类学生虚仿系统学习效果评价指标体系

部分指标说明如下。

1) 协同交互：虚仿实验中与其他成员的沟通协作能力；

2) 应变分析：对虚仿实验设计的突发情况处理与分析的能力。

除上述2个指标外，其余指标在文献 [7] 中均有详细说明。

3. AHP-结构熵权法组合赋权

3.1. AHP评价模型

层次分析法将同一层次的指标两两比较的重要性进行定量描述，能够快速梳理复杂的多指标问题。层次分析法步骤如下 [9] ：

1) 建立层次结构模型，包含目标层、准则层和方案层；

2) 采用“1至9相对重要性标度法”，两两比较各指标之间的重要性，构建比较判断矩阵A；

3) 计算判断矩阵的最大特征值、特征向量和各指标权重。计算步骤如下：

第一步，计算判断矩阵每行因子的乘积 $M_i$ ：

$M_i={\displaystyle \underset{j=1}{\overset{n}{\prod }}{a}_{ij}}$ (1)

式中， $a_{ij}$ 为判断矩阵A中的元素。

第二步，由上得到的 $M_i$ 值，计算其n次方根，其中n为判断矩阵维数：

${\bar{w}}_i=\sqrt[n]{M_i}$ (2)

第三步，按式(3)得到各指标归一化权重：

$w_i=\frac{{\bar{w}}_i}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\bar{w}}_i}}$ (3)

4) 进行一致性检验，首先计算判断矩阵的一般一致性指标CI (式(4))，再计算随机一致性指标CR (式(5))，CR值小于0.1说明通过一致性检验，反之则未通过一致性检验。

$\text{CI}=\frac{{\lambda }_{\max }-1}{n-1}$ (4)

$\text{CR}=\frac{\text{CI}}{\text{RI}}$ (5)

下表1为RI取值。

Table 1. Ri Table of random concordance

表1. 随机一致性RI表

3.2. 结构熵权法模型

结构熵权法将定性与定量分析相结合，能较大程度避免由专家主观意志带来的局限性，其主要步骤如下 [10] ：

1) 采集专家意见，进行“典型排序”：

首先根据“德尔斐法”对专家意见进行调查，将各指标按照重要程度进行排序，调查形式如表2所示。

Table 2. Structure entropy weight method expert survey sketch

表2. 结构熵权法专家调查示意

注：表中每位专家的指标排序均按照重要程度由高到底依次排列，即排序为“1”的指标在4个指标中重要程度最高，排序为“4”则代表该指标重要程度最低。

2) 对“典型排序”进行“盲度”分析：

由h位专家对n个指标的排序矩阵记为A ( $A={\left(a_{ij}\right)}_{h\times n}$ , $i=1,2,\cdots ,h$ , $j=1,2,\cdots ,n$ )，称为指标的“典型排序”矩阵，其中 $a_{ij}$ 表示第i个专家对第j个指标 ${\mu }_j$ 的评价。定义隶属函数为

$\mu \left(I\right)=\frac{-\ln \left(q-I\right)}{-\ln \left(q-1\right)}$ (6)

其中I代表专家给出的排名序号。假设有4个指标A，B，C，D，如果指标A最重要，对应的I = 1，如果A第二重要，那么I = 2，以此类推。 $\mu$ 是定义在[0, 1]上的变量， $\mu \left(I\right)$ 为I对应的隶属函数值， $I=1,2,\cdots ,j,j+1$ ，j为实际最大顺序号，表示一共有j个指标参与排序。q为转化参数量，这里取 $q=j+2$ 。将 $I=a_{ij}$ 代入式(7)，得到定量转化值 $b_{ij}$ ，它是I的隶属度。假设每位专家对于指标 ${\mu }_j$ 有相同的“话语权”，我们得到专家对于第j个指标的平均认识度：

$b_j=\frac{b_{1j}+b_{2j}+\cdots +b_{kj}}{k}$ (7)

定义 $Q_j$ 为专家对第j个指标的认知的不确定性，称为“认知盲度”：

$Q_j=\left|\frac{\left[\max \left(b_{1j},b_{2j},\cdots ,b_{kj}\right)-b_j\right]+\left[\text{mix}\left(b_{1j},b_{2j},\cdots ,b_{kj}\right)-b_j\right]}{2}\right|$ (8)

于是对于每一个指标 ${\mu }_j$ ，全体专家对它的总体认识度，记为 $m_j$ ，得到

$m_j=b_j\left(1-Q_j\right)$ (9)

3) 归一化处理：

通过归一化处理得到各指标权重

${\alpha }_j=\frac{m_j}{{\displaystyle \underset{j=1}{\overset{n}{\sum }}{m}_j}}$ (10)

其中 ${\alpha }_j$ 为各个指标权重

3.3. 综合评价模型建立

为使得该评价体系能够兼顾专家的教学经验与学生的真实体验，依据式(11)进行综合权重的计算。

${\beta }_i=\frac{\sqrt{{\alpha }_i{w}_i}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\sqrt{{\alpha }_i{w}_i}}}$ (11)

其中， ${\alpha }_i$ 为结构熵权法确定的指标权重， $w_i$ 为层次分析法确定的指标权重。

4. 实例分析——S大学虚仿实验系统学习效果评价

以S大学经济管理学院市场营销虚仿实验平台为例。本文以图1所示评价体系为基础，对使用学生共发放110份问卷，回收有效问卷102份问卷，问卷有效率率92.7%；对教学专家共发放10份问卷，回收有效问卷10份问卷，回收率100%。

4.1. AHP确定权重

1) 对来自学生的102份问卷进行均值统计，构造一级指标层的判断矩阵，按照前述层次分析法步骤进行计算。判断矩阵及所得各指标权重如表3所示。

Table 3. The weights of the first-level indicators based on AHP

表3. 基于AHP的一级指标层权重

经计算，该判断矩阵最大特征根为3.094，CR值为0.09，通过一致性检验。

2) 构造各一级指标下设的二级指标层判断矩阵，以过程层面为例，权重结果如表4所示。

经计算，该判断矩阵最大特征根为3.065，CR值为0.062，通过一致性检验。

依次计算其它二级指标相对其所属一级指标的权重，二级指标层计算结果如下表5，所构造各判断矩阵均通过一致性检验。

3) 计算各三级指标相对其所属二级指标的权重，所构造各判断矩阵均通过一致性检验，结果如下表6所示。

Table 4. The weight of the two-level index layer based on AHP

表4. 基于AHP的二级指标层权重

Table 5. The relative weights of the secondary indicators based on AHP

表5. 基于AHP的二级指标相对上级权重

Table 6. The relative weights of the three-level indicators based on the analytic hierarchy proces

表6. 基于层析分析法的三级指标相对上级权重

4) 各三级指标相对于目标层的最终权重可由其相对上一级权重与所隶属的一级、二级指标权重依次相乘获得。基于层次分析法的三级指标最终权重如表11所示。

4.2. 结构熵权法确定权重

1) 回收问卷，统计10位专家对各级指标的排序意见。表7所示为10位专家对三个一级指标的“典型排序”。

Table 7. Typical ranking of Tier 1 indicators

表7. 一级指标的典型排序

2) 依次计算各指标平均认知度、认知盲度、总体认知度和归一化权重，计算结果如下表8所示。

Table 8. The weights of the first-level indicators based on the method of structural entropy

表8. 基于结构熵权法的一级指标层权重

3) 重复上述步骤，依次计算各二级、三级指标相对其上一级指标的权重。表9为二级指标权重计算结果，表10为三级指标权重计算结果。

Table 9. Relative superior weight of two-level index based on structure entropy weight method

表9. 基于结构熵权法的二级指标相对上级权重

Table 10. The relative superior weight of three-level indexes based on structure entropy weight method

表10. 基于结构熵权法的三级指标相对上级权重

4) 各三级指标相对于目标层的最终权重可由其相对上一级权重与所隶属的一级、二级指标权重依次相乘获得。基于结构熵权法的三级指标最终权重如表11所示。

Table 11. Evaluation index system and weight of virtual learning system for students of Economics and management

表11. 经管类学生虚仿系统学习效果评价指标体系及权重

4.3. 组合权重确定及权重对比

按照式(11)计算最终的组合权重，计算结果如下表11。

由表11可以得出，在三级指标层面，学生意见与专家意见形成较大分歧。在虚仿实验过程中，学生明显更加重视“明晰问题”“学习调整”“同化性迁移”等能衡量短时间内学习成果的指标；而“认同感”“自我效能感”“学习适应”等衡量长时间内学习思维、情感的指标则被忽略。

由图2可知，在虚仿学习过程中，学生高度关注“体验与交互”的感受；在“情感层面”，学生认为“学习价值观”重要程度低于“学习意志”，专家意见反之；与专家意见相比，学生意见下的“情感层面”重要程度更低，而“知识层面”双方意见相仿。

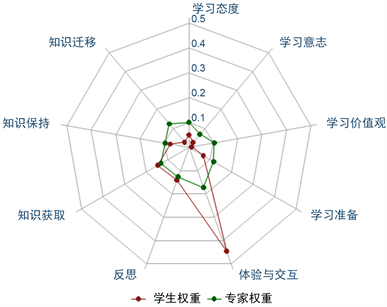
Figure 2. Comparison of the weights of the two-level indicators from students and experts perspectives

图2. 学生角度与专家角度二级指标权重对比

由图3可知，组合后的权重大体上与专家意见下的权重相近，在“学习调整”和“知识深加工”指标上，组合权重要显著高于专家角度权重，因为学生力图更好地完成下次虚拟学习，故更加重视每次虚仿实验后的反思与调整。“知识迁移”的三个指标的组合权重均低于专家角度权重，这与学生在实际学习中更注重学习成绩和知识掌握程度、轻视知识应用与迁移的特点相符，说明将两者意见相结合的权重更加客观，贴合实际学习情况。

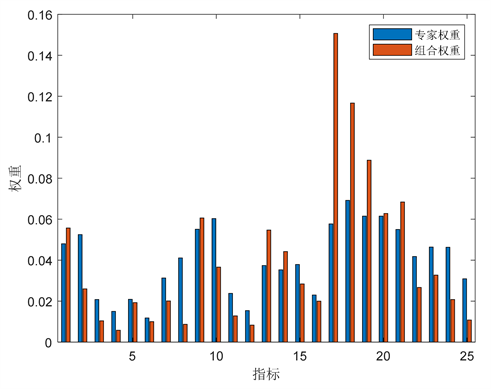
Figure 3. Comparison of three-level index combination weight and expert angle weight

图3. 三级指标组合权重与专家角度权重对比

5. 结语

本文提出AHP-结构熵权法进行虚仿实验系统学习评价体系指标组合赋权，将领域内专家的优势经验与学生参与虚仿实验的真实体验结合，给出了更为客观、准确的经管类虚仿实验系统学习效果评价体系及指标权重，为虚仿实验系统的开发和维护提供了科学参考。

基金项目

北京市级大学生创新创业训练计划资助项目(批准号：202310004147)

NOTES

^*通讯作者。