1. 引言
目前,交通拥堵和效率低下已成为一个全球性问题。发达国家和发展中国家城市人口急剧增加所造成的最直接问题就是车辆数量的增加和交通堵塞。提高交通效率是改善日常交通状况的重要方法,当下大数据的兴起也为提高交通效率提供了新的解决方案。各个城市每天都会产生大量的交通数据,随着大数据处理的快速发展,这种存储的数据信息开始发挥作用。通过对大数据中的数据信息进行分析和处理,可以提出解决交通问题的新思路。
当前,全球对智能交通系统 [1] 的投资正在增加。智能交通系统有许多环节,包括交通量预测,在智能交通控制和动态控制中起着重要的作用。借助准确的预测结果,通勤者可以选择合适的交通方式、出行路线和出发时间,实现诱导前提。同时,实时、准确的路网短期交通流量预测有助于更好地分析路网交通状况 [2] ,在道路网络的交通规划和交通管理优化中发挥着重要作用。在构建智慧城市中,实时预测交通量是亟待解决的问题。
现有的短期交通量预测模型 [3] - [16] ,如神经网络方法 [7] ,具有复杂的误差面。如果在计算过程中不小心,神经网络会陷入局部极小点,容易造成评估结果出现偏差。还有一些AR模型 [6] ,其中相位会影响频谱峰值的位置,噪声会降低频谱估计等。此外,交通量预测也存在数据缺失、冗余等问题,也会受上下游路段流量影响。交通量数据受各方面因素的影响,具有稳定性差、随机性强、高度非线性等特点,使得交通量预测非常困难。
综上所述,现有模型都存在着不容忽视的缺点,结合交通量的复杂性和易受其他因素影响的特点,可以得出结论,目前用于交通流预测的模型不足以满足本文的交通量预测的真实需求。本团队提出了一种利用高斯过程回归模型(GPR) [15] 的交通量预测方法。GPR是一种全新的机器学习算法,它是基于贝叶斯理论和统计学习理论发展起来的,与ARIMA [6] 、支持向量积回归 [3] 。等方法相比,GPR不仅能够预测未知量的期望值,还能给出其分布状况;与传统的区间预测方法相比,GPR又具有机器学习算法泛化能力强等优点。此外,GPR模型参数较少,能自适应获取其超参数。因此GPR可以直接、方便地用于概率性预测 [17] 。GPR有严格的统计学理论基础,不仅能够处理低维数、小样本、非线性等复杂回归问题,而且也适用于大样本和高维情形的扩展算法,还具有参数自适应获取和预测结果具有概率意义等优点。并且GPR模型在其他领域已经取得了成功应用 [18] 。综上所述,高斯过程回归模型满足了本文对交通量预测的实际需求。
2. 基于高斯回归过程的短时交通量预测
2.1. 高斯回归过程 [19]
高斯过程是随机过程的一种,适用于处理小样本、随机性强及含多维复杂因素的饱和负荷预测问题 [18] [20] [21] [22] 对于训练集
,其中
为一组训练输入变量,
为目标输出向量。输入变量的随机过程状态集合
服从n维联合高斯分布,因此f属于高斯过程,其概率函数用GP表示,可通过均值函数
及协方差函数矩阵
确定 [23] ,即
(1)
高斯过程回归模型将输入变量X与目标输出y之间的关系视作高斯过程f;把独立的白噪声
考虑到f,则可建立标准高斯过程回归模型:
(2)
式中:
为白噪声,服从高斯分布,即满足
,I为单位阵,
为方差。由于白噪声具有独立性,因此y同样属于高斯过程,即
(3)
根据贝叶斯原理,在给定的训练集D内,建立y的先验分布:
(4)
则对测试样本
,根据高斯过程的性质,训练样本的目标输出y与测试样本输出
服从联合高斯分布:
(5)
式中:
为训练输入变量X的
阶协方差函数矩阵,
为核函数;
为训练输入变量X与测试输入变量
的
阶协方差函数矩阵;
为测试输入变量
自身的协方差。
利用贝叶斯后验概率公式,在给定测试输入变量
与训练集
的条件下,对应的输出
满足:
(6)
式中:
和
分别是测试样本输出
的均值和方差。
则高斯过程回归预测模型为:
(7)
(8)
利用高斯分布的“
原理”,测试样本输出
预测值99.73%的置信区间为:
(9)
2.2. 分析步骤
用高斯回归过程精准预测短时交通量。如图1所示。
1) 收集若干交通量的历史时间序列数据,得到
。
2) 当交通量数值变化差异较大时,会对高斯过程学习造成不利影响,因此需要对交通量进行归一化处理,具体为:
(10)
式中:
和
为最大值和最小值;x为原始值。
3) 交通量数据划分为训练集和测试集,建立标准高斯回归过程模型,根据贝叶斯原理,建立y的先验分布。
4) 对高斯过程回归模型进行参数选择和调整之后,将训练所得模型在测试样本上进行测试,通过评价指标可知,高斯过程回归模型对数据的拟合效果较好 [24] 。
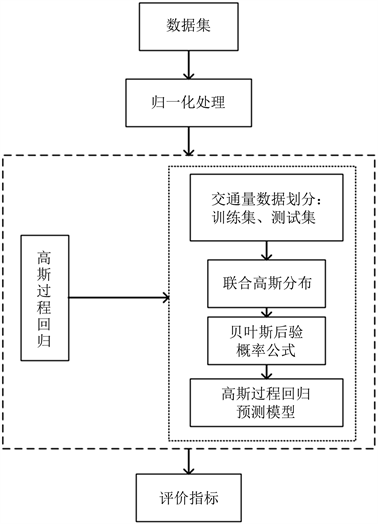
Figure 1. Flowchart of the analysis procedure
图1. 分析步骤流程图
3. 案例应用与分析
3.1. 数据说明
为了测试GPR模型的短时交通量量预测性能,数据采用重庆市某主干道2019-10-11 00:00:00至2019-10-31 20:00:00的每5分钟的交通流量,得到6000个样本,如图2所示。前3000个样本作为训练集,其余样本作为测试集。
为了更加方便地使用数据,消除奇异样本点对整体数据的不良影响,将采集到的数据进行归一化处理。
3.2. 评价指标
针对短时交通量不确定性区间的特点,本文采用无效覆盖率(KP)和区间宽度(Width)两个评价指标,它们定义为:
(11)
式中:
(12)
(13)
式中各表达式含义与KP相同 [25] 。
3.3. 预测结果分析
将交通量数据进行划分后,对数据进行归一化处理。在MATLAB中,再对已经归一化处理后的数据集进行高斯回归过程处理。预测结果如图3所示:
本文使用GARCH [7] 、BOOTSTRAP模型 [25] 与本文所提模型进行预测结果评价指标的对比,各模型的评价指标如表1所示:

Table 1. Evaluation indicators of different models
表1. 不同模型的评价指标
由表1可知,本文模型相较于GARCH,KP和Width分别提高了0.6%、18.59;相较于BOOTSTRAP,KP和Width分别提高了0.24%、6.34。结果表明,本文模型表现出的性能最优。
4. 结论
高斯过程回归模型(GPR)具有机器学习算法泛化能力强、模型参数少、超参数自适应采集、统计学理论基础严格等优点,可以直接方便地用于概率性预测。在此基础上,本文建立了高斯过程回归模型作为道路交通量状态动态分析和预测的方法。并通过将高斯过程回归模型与GARCH、BOOTSTRAP模型进行对比,发现高斯过程回归模型表现出的性能最优,且对数据有很好的拟合效果,满足了我们一开始希望通过高斯过程回归模型预测交通量、减少交通拥堵等问题的设想。综上,高斯过程回归模型满足了本文对交通量预测的实际需求。
基金项目
重庆交通大学大学生创新创业训练计划项目《城市道路短时交通流预测研究——以重庆市某主干道为例》(S202210618027)资助。重庆交通大学大学生创新创业训练计划项目《一种新型混合模式在短时交通流预测中的应用研究》(S202210618039)资助。