校际教育资源分配对学生学业表现影响探究——基于PISA科学素养数据

Research on the Influence of Interschool Educational Resource Allocation on Students’ Academic Performance—Based on PISA Science Literacy Data

摘要: PISA学生素养评估计划在测试内容、方式和规模上都为国际领先水平，充分利用其数据资料，对把握学生发展有积极意义。文章基于因子分析及多层线性模型开展，研究学生个人和校际因素对学业表现的具体作用情况。结果表明：学生学业表现不仅受到个人影响，还会因为学校条件受到影响。个人层面中，起到积极作用的是学生态度和家庭经济条件；而学生感知的来自老师的期望，逆反心理，焦虑感等都起到负面影响。添加校际层面地理位置和资源投入因子的交互作用后，个人层面的影响力可能会被加强或削弱。对院校间资源的优化配置能够改善个人或家庭因素带来的负面影响。

Abstract: The PISA student literacy Assessment program is internationally advanced in terms of test content, method and scale. Making full use of its data is of positive significance for grasping student development. Based on factor analysis and multi-layer linear model, this paper studies the specific effects of individual and inter collegiate factors on academic performance. The results show that students’ academic performance is not only affected by individuals, but also affected by school conditions. At the individual level, students’ attitudes and family economic conditions play a positive role. However, students’ perceived expectation from teachers, rebellious psychology, anxiety and so on all play a negative role. The influence at the individual level may be strengthened or weakened by the inter collegiate level inter action between geographic location and resource investment factors. The optimal allocation of resources between colleges and universities can improve the negative impact brought by individual or family factors.

1. 引言

“努力让每个孩子都能享有公平而有质量的教育” [1] ，教育改革发展的两大要求，一是以公平为前提，着重于教育资源的分配；二是围绕“质量”两字，着重于教育品质的提高。其中，公平处于先行位置。教育公平始终是社会公众关注的民生大事。

建国以来，我国的教育综合水平得到了很大的提高。但由于社会经济发展的历史原因，我国的教育仍旧存在着一定的供需矛盾 [2] ，并在区域间、城乡里、院校中以及经济群体内表现出资源分布不均现象。结合以往PISA的测试数据，中国学生在整体平均素养表现上都处于领先地位，但同时存在于学生间的巨大差异也是不可忽略的重点，教育公平始终是亟待提升的重点 [3] 。

我国对于教育资源配置问题的研究起步较晚，开始主要集中于定性研究，形式是结合理论与实际现象分析教育资源配置的现状及原因。之后，逐渐在研究中加入定量分析，并实现了从简单的单因素相关分析到多因素实证分析的转变。总结来看，教育领域对于资源公平配置的研究主要遵循两种基本范式：一类主要存在于教育社会学，利用单个指标或建立一个指标体系 [4] [5] 展开对教育不公平现象的分析和评价，指出症结所在并提出处理建议；二类主要存在于教育经济学，利用各类统计指标(如极差、基尼指数、Theil系数等) [6] [7] 或统计方法(如侧重衡量投入产出效率的DEA模型 [8] 、侧重变量拟合的回归模型 [9] 等)来验证教育不公平现象的存在。其中，由于教育数据表现出的嵌套结构，多层线性模型在教育领域的应用十分广泛。多层线性模型在引入多变量时，不仅在单个层面进行，还能引入第二层面变量，分析两层面的交互作用，这便于我们揭示个体和群体的关系。基于此，本文聚焦学生个人和校际维度，研究影响学生学业表现的个人因素，引入校际因素，探究两层面的相互作用情况。这对于我们把握学生情况，调整沟通与教学方式，提高育人整体效率，促进教育均衡发展具有正向作用。

2. 研究准备

2.1. 模型概述

多层线性模型(HLM)是基于普通线性回归分析发展而来的可同时处理个体和群体数据的统计分析方法。其在处理嵌套型数据时，在模型参数估计、数据解释力上相对传统线性回归更具优势。

在建模时，多层线性模型先以第一层级的自变量( $X_m$ )对因变量( $Y_{ij}$ )建立回归方程；再将其中的截距( ${\beta }_{0j}$ )及斜率( ${\beta }_{1j}$ )作为因变量，以第二层级自变量( $W_n$ )作为自变量，建立回归方程。由此得到的方程在二层级上拥有相同的截距和斜率，又在一层级上受到个体变量的影响。模型基本形式如下：

$\{\begin{array}{l}{Y}_{ij}={\beta }_{0j}+{\beta }_{1j}{X}_m+{\epsilon }_{ij}\\ {\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{W}_n+{\mu }_{0j}\\ {\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{W}_n+{\mu }_{1j}\end{array}$ (1)

其中， $Y_{ij}$ 为因变量，i表示第一层级各变量单位。X和W分别代表一层级和二层级的自变量，m和n分别为一层级和二层级的变量个数。 ${\epsilon }_{ij}$ 、 ${\mu }_{0j}$ 、 ${\mu }_{1j}$ 为模型的随机效应，即未被纳入模型，无法解释的部分。 ${\beta }_{0j}$ 、 ${\beta }_{1j}$ 分别为截距和斜率。

2.2. 建模思路

中国城乡、区域之间因教育资源配置不平衡，继而造成悬殊的教育水平差距，是中国教育的基本国情。学校所处地域不同，其享有的资源也相差巨大，无论是以教师数量和质量为代表的人力资源还是以教学设备和实验设备为代表的硬件资源。学校作为重要的学习场所，是学生学习最直接的外部环境。在同一所学校学习的学生受到的外部影响条件相似度极高，包括学校学习资源、学习氛围等。由于“群体效应”的存在，学生学习行为和学习效率也呈现一种高度的相似性。此时，传统线性回归的独立性条件不再满足，但多层线性模型就能做到较为精确的估计。在同一所学校学习的学生内部差异远小于院校间的差异性。基于以上，学生学业表现不仅受到个人因素的影响，还会受到学校层级的影响，故在研究学生学业表现影响因素时，对个人和学校两个层级进行分析是有必要的。

因此，本研究拟通过多层次线性模型从学生个体和学校两个层次分离出其对学生学业表现差异的不同效应，着重探究校际层面的资源投入所引发的学生学业的差异。

2.3. 数据来源

本文利用来自PISA项目的第一手数据。PISA是一项国际层面的学生能力评估计划，在全球72个国家、地区抽取15岁中学生样本对其综合科学素养展开调查测评。其中，在中国地区(北京、上海、江苏、广东)进行的测试，通过PPS抽样方式共抽取268所院校的9841名学生样本参与，抽取不同层级中的样本，确保样本涵盖总体的各部分，从而提高测试结果反映总体的可信度。数据清洗完毕后，本文最终获取有效数据6003条。PISA调查包括背景问卷和素养评估两部分，一是针对学生、教师以及学校的背景问卷，问卷数据在每个指标大类下设有1~20个问题不等，均以量表形式设置问题，得到多角度主观感受数据；二是对学生进行的综合科学素养测试，范围覆盖小学到中学的知识和技能，得到较为客观的成绩数据。此数据结合主观自评和客观事实，利于模型全方位地分析和解释学生的学业表现情况。

3. 实证分析

本文选定因变量(被解释变量)为学生的科学素养得分，即问卷数据中科学能力成绩(PV1SCIE - PV10SCIE)的算术平均值。PISA数据显示，中国学生科学素养表现平均分528.05，标准差为95.40，偏度为−0.28，峰度为−0.42。OCED国家学生科学素养平均分为494.84，标准差为94.14，偏度−0.03，峰度−0.53。虽然我国学生的素养平均水平高于OCED国家学生，但学生群体间差异相对显著。北京、上海、江苏、广东均属于经济及教育相对发达地区，其学生的群体差异尚且显著，国内各地区间的学生差距更为悬殊。探索产生差异的原因，对于我们改进教育水平有重要意义。

另外，选定自变量(解释变量)分两个水平方面：第一水平(学生层面)和第二水平(校际层面)的指标共51个。学生层面指标包括学生个人信息、经济情况、心理情况等，从多角度对学生个体展开评分；校际层面指标包括学校的地理位置(具体指学校所在城市的规模大小)和相关资源配置(人力、教学设施配置、实验条件等)情况(表1)。

Table 1. Primary index system

表1. 初选指标体系

由于大类下指标显著相关，由此产生的多重共线性会对建模效果有不利影响。为了避免模型失真和估计不准确的情况出现，本文考虑引入因子分析，同时达到对指标降维，简化模型的作用

3.1. 因子分析

经过SPSS对数据的分析计算，得到结果，KMO和巴特利特球度检验值为0.89，说明数据适合做因子分析。软件将31个学生层面的指标群，简化输出8个共性因子，累计方差贡献率达到63.99%。根据旋转后的成分矩阵，对提取的共性因子进行命名。

根据因子解释的主要方面依次命名为焦虑因子、态度因子、社交因子、期望因子、经济因子、逆反因子、娱乐因子、性别因子(表2)。

Table 2. First level factor information table

表2. 第一层面因子信息表

接着对第二层面数据做因子分析，KMO和巴特利特球度检验值为0.74，软件将7个指标群简化，提取出2个因子，累计贡献率达到52.3%。V₁主要解释学校在实验设备的投入和使用情况，师资力量及教师发展投入的情况，因此命名为资源投入因子；V₂主要解释了学校所处的城镇，因此命名为地理位置因子(表3)。

Table 3. The second layer factor information table

表3. 第二层因子信息表

经过处理后，第一层的变量变为G₁~G₈八个不同维度的因子，第二层的变量变为V₁，V₂两个因子。表4为因子得分结果。其中学生个人层面，逆反因子G₆和娱乐因子G₇表现出严重的偏态分布。偏度值分别为2.84和2.23，对应峰度值10.22和10.52，即这两者在右侧的存在极大值，并在均值左侧呈尖峰分布。通俗来讲，存在学生对老师表现出显著的逆反心理，但多数学生表示与老师较为融洽；同理，有少数学生表现出较高的娱乐性，这可能对学生的学业表现有一定影响。

Table 4. Factor score information table

表4. 因子得分信息表

另外校际层面，资源投入V₁也表现出较明显的偏态分布，偏度值为−1.44，峰度值为1.0，这是左偏和尖峰分布。整体来看，学校资源投入评分在均值左端存在极小值，即有学校表现出严重资源不足的问题。V₂地理位置峰度值为−0.22，相对正态分布较平缓，说明不同学校的地理差异比较明显。

因子分析显示，学生在个体层面和校际层面都表现出了显著的差异，这与实际情况相符。下面借助多层线性模型对两个层面的影响方式作出具体测定。

3.2. 多层线性模型

首先引入模型1 (零模型)，检验HLM分析法的适用性。

零模型不包含任何自变量，仅包括学校层面的随机效应。这能够确定学生学业表现中由学校层面产生的变异比例，以此来检验数据是否适合运用多层线性模型进行分析(表5)。

Table 5. Summary table of null model results

表5. 零模型结果汇总表

$\{\begin{array}{l}{Y}_{ij}={\beta }_{0j}+{\epsilon }_{ij}\\ {\beta }_{0j}={\gamma }_{00}+{\mu }_{0j}\end{array}$ (2)

引入HLM软件分析后的零模型结果显示，在方差分析中，组间方差分量(校际差异)为0.546，对应P值接近于0，统计学显著，说明校际间学生学业表现差异显著，具有明显的校际隔离。组内相关系数ICC = 0.546/(0.546 + 0.481) = 53%，即学生学业表现的差异中有53%由学校层面影响，高占比决定了校际差异属于不可忽略的组间差异，因此采用多层线性模型分析是合适的。

接着引入模型2、3、4：定义模型2为随机效应回归模型，只包含学生个人层次变量，但允许个人层次方程的系数和截距在校际随机变化，着重衡量学生个人层面变量对学业表现的作用。模型3在控制学生个体层次变量的基础上，在截距项加入学校层面变量，衡量学校对学生学业平均表现的直接效应，并允许个体层面各变量在校际间随机变化，可以说，这是完整模型的一个特殊变异。最终的模型4为完整模型，在模型3的基础上，继续在一层变量的回归系数中加入学校层面变量影响(校际因素同时作用与截距和斜率)，通过学生个体和学校的交互作用结果探究其对学生学业表现差异的作用过程，即学校对学业表现差异的间接调整作用，两层次的系数符号相同则说明起到加强作用，反之起削弱作用。

模型4完整形式如下：

$\{\begin{array}{l}{Y}_{ij}={\beta }_{0j}+{\beta }_{mj}{G}_m+{\epsilon }_{ij}\\ {\beta }_{0j}={\gamma }_{00}+{\gamma }_{0n}{W}_n+{\mu }_{0j}\\ {\beta }_{mj}={\gamma }_{m0}+{\gamma }_{mn}{W}_n+{\mu }_{nj}\end{array}$ (3)

事实上，模型4假定是最符合实际情况的，即学生的绝对水平在校际间存在差异，并且校际因素能够作用于学生个人，间接影响学生的各方各面。不同的院校有各自的文化，通过营造不同的氛围来影响学生。例如就读于不同院校的学生对学习的兴致不一，对于集体的感知度有差异，焦虑程度也或轻或重。

经过拟合，模型2、3、4对应的组内相关系数ICC分别为51.2%，47.9%，47.7%，模型的组间差异不断减小。固定效应表示一层(学生)和二层(学校)的自变量对学业表现差异的影响效果，随机效应表示自变量所没有解释的差异。具体建模结果如下表6所示。

Table 6. Model result table

表6. 模型结果表

注：^*即P值 < 0.05，^**即P值 < 0.01，^***即P值 < 0.001；加粗为个人层面因子。

具体多层线性模型结果示意图如图1所示。

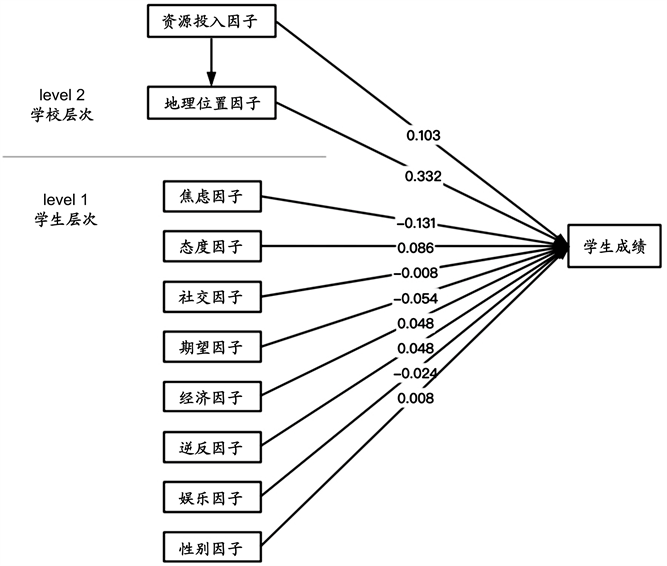
Figure 1. Schematic diagram of HLM model

图1. 多层线性模型示意图

经过分析，可以得到以下结果。

1) 个人层面。在学生个人层面中，对学生学业表现有正向影响的因素有态度因子(0.086，0.1%水平下显著)，经济因子(0.048，0.1%水平下显著)。学生良好的学习态度是提升学业表现的必然要求，而一定程度的经济状况对学生学业表现也表现出显著的正向影响。对学生个人而言，学习态度是影响学业表现的最直接条件，态度端正与否能够直接决定学生学业表现的优劣走向；同时，学生经济条件好，其学业表现也会相对优异。经济条件较好的家庭，有意愿和有能力让孩子获得更好的教育资源，从而在学业表现上更优异。此时教育不平等主要表现在教育获得的质量差异上 [10] 。但是，当经济条件达到一定阈值之后，这个效用就会停止扩张。经济条件提升不会无限制的正向促进学生学业表现。对比两因素，显然学习态度起到的效用更大。相同条件下，态度因子影响力是经济因子影响力的1.79倍。

对学生学业表现呈现显著负向影响的因素有焦虑因子(−0.131，0.1%水平下显著)，期望因子(−0.048，0.1%水平下显著)，逆反因子(−0.054，0.1%水平下显著)，娱乐因子(−0.024，1%水平下显著)。学生个人心理状况，生活、社交情况及对外界期望感知等都对其学业表现都有显著的影响。具体来说，学生心理状态越不稳定，焦躁、急切等心理都会反向作用学业表现。当学生感知到老师对自己有较大期望时，反而对其学业表现有一定的负面影响；同时，当学生对老师有逆反情绪时，其学业表现必然也会受到一定损伤。在以上起负面作用的因子中，影响力效果排序是焦虑因子 > 逆反因子 > 期望因子 > 娱乐因子，若娱乐因子的影响力为1，则期望、逆反、焦虑因子影响力以此为1，2，2.25，5.46。

2) 学校层面。校际层面引入主要分为对截距和因子系数影响，对应表6模型3，模型4的相关数据。截距方面，学校层面的资源投入因子(0.103，0.1%水平下显著)和地理位置因子(0.332，1%水平下显著)都呈现正向影响，即学生学业表现的平均成绩受到这两项因子的影响，学校的资源投入越高，学校的地理位置越好(所处城市的规模越大)，学生学业表现的平均成绩越高。相同条件下，地理位置因子的影响力是资源投入的3.22倍。这可解释为城市规模在一定程度上与资源分配情况呈正相关影响。

因子系数方面，结合模型4回归系数一列，整理得，学校层面因子影响显著并对个人层面因子起到加强作用的组合是地理位置因子和期望因子。通俗解释，越是大城市的学生，对于老师给予的高度期望，表现出更强烈的负面影响。这表明，大城市的学生的自我观念可能更强烈。

学校层面因子影响显著并对个人层面因子起到削弱作用的组合较多，地理位置因子分别与焦虑、态度、娱乐因子构成作用削弱组合。学生所在城市越大，心理焦虑和爱好娱乐引发的负面影响会被削弱，与此同时，端正的学习态度带来的正面影响也被削弱。这可以解释为，大城市学生的抗压能力会相对较强，同时由于他们的学习资源会更丰富，所以学习效率也会更高。另外，资源投入因子与经济因子构成作用削弱组合。学生的学业表现受到家庭经济情况正相关，但这个削弱组合显示随着学校资源的投入，学生学业表现受到家庭经济影响的效用就会越低。它直接向我们证明了，推进基础教育资源平衡是极其重要的。

4. 结论与启示

4.1. 结论

1) 校际因素对学生发展有重大影响

零模型显示，组内相关系数为0.53，说明学校层面可以解释学生学业表现差异的53%。学生学业表现具有明显的层级特征，校际因素对学生学业表现至关重要。我国人口较多，但资源有限，不同地区得到的社会资源差异较大。学校地理位置越好，得到的资源越多，学生学业表现的成绩越好。

同时，参与调查的数据显示，处于较好地理位置的学校和学生家庭水平间也有正向的关系。但校际因素对于学生的影响作用不一定是直接的，一方面好的学校能够通过创建好的学习文化直接作用于学生个人，正向导向学生的学习态度等来实现学业的发展；另一方面通过吸引较好家庭、个人条件的学生来入学使得学生总体学业表现的提升。这种现象的存在会使得院校间的差距越来越大。

2) 学生个人因素对其自身发展起直接作用

个人因素对学生学业发展有直接作用力。模型也向我们展示了，学习态度和经济水平因子对学生的学业表现有正向作用。焦虑、逆反、期望和娱乐因子则起反向作用。学生心理健康、个人态度、社会表现这类主观性变量具有的高解释力，证明从个体层面改善学生学业表现是有操作可能的，并且也向我们暗示了学校和家庭可以大有作为的方面。

3) 学生个人和学校因素对学生发展有交互作用

学校和学生因素间的交互是复杂的。不论是地理位置因子还是资源投入因子对学生层面的因素都有加强和削弱两方面。根据模型4的结果，我们对不同校际间的学生有一定的认识，对于不同校际间的学生应当有针对性的调整策略。处在大城市学生生活的学生们，表现出了更高的抗压能力和自我主张。他们更能承受焦虑感，比起来自老师的期望，学生更希望以自我感受为主体。

同时由于大城市教育投入高质量好，对学生个人层面的要求就会降低。具体表现是相对于资源少的乡村学生，大城市学生想要取得更好的学业表现时在学习态度、家庭经济情况和时间投入等方面的要求宽松得多。合理的利用两层面的交互作用能够更精准有效地调整学生情况，进而去正面影响学生学业表现。

4.2. 启示

上文的数据实证，对把握我国中学生教学教育有一定的借鉴意义。基于此，我们分别针对学生、学校、教师和社会给出启示：

1) 学生占据教育主体地位，应当充分发挥主观能动性

学生在教育中是特殊的存在，他作为客体的同时更是主体。他的主体性一方面表现在学生主体对教育结果的高度影响力，另一方面则是学生的主观能动性。因此，学生应当充分利用这一特性，调整自我状态，树立学习观念，转变学习方式，进而提高个人的学业素养。

学生在学习进程中需要一个良好的学习观作指引。为了使学生更好的认识学习和投入学习，一个正确的学习观是极其必要的。需要强调得是，学习是个人发展的客观需要，它帮助学生认识、充实和发展自我，是发现个体个性和魅力的过程。其次学习不受限于时间和空间，学生不应拘泥于学习场所和时间。

2) 学校应注重自身资源的分配

学校对学生的发展有关键作用，学校需在能力范围内合理分配资源。一方面应当为学生搭建坚实的硬件基础，为学生创造一个有利的学习环境。另一方面，学校也应注重师资力量的壮大和教师后续的发展。教师队伍规模是一方面，队伍整体水平的与时俱进也是不容忽视的一方面。因此，一部分的资源应投入到教师身上，使得教师在工作的同时也能让自身得到发展。如今，信息化建设处于一个快速推进的阶段，利用网络工程，学校能够为学生提供优质的数字教育资源，同时也能为教学提供参考，转圜资源短缺的矛盾。

除此之外，对学生心理状态也不可轻视。学生个人所感知到的氛围对其学业成绩是有影响力的 [11] 。因此，学校通过创建良好的文化氛围来改善学生整体的心理状况，进而提高学业表现也不失为一种好方法。

3) 教师应主动有效地发挥自身主导作用

教师的主导作用是教学存在的标识，而教师能否科学地帮助学生、督促学生、引导学生，是提高学习效能和教育产出的关键。教师应当以学生主体为中心，充分发挥主导作用。虽然教学形式上从以往的内容引导、知识引导转化成学习方式的引导、逻辑能力的培养和学习思维的激发，但本质上教师的主导作用没有变。课堂上，教师依旧需要组织课堂纪律，设计教学方式方案，引导学习进程；课堂下，教师需观察学生生活，了解学生心理，在引导其健康发展的同时，切忌对学生过分寄托期望，做到有鼓励但不过激。

同时，教师对自身发展也应投入更多关注。在学科能力方面，教师承载着家长、学校、社会的信任，须始终保持自主完善和自主提高，掌握系统的知识体系是对个人和学生负责的体现；在个人成长方面，不应仅将职业作为一种谋生手段，应始终保持追求保持上进。横向与同事比较，纵向与自身相比，不断地查漏补缺，求得个人良好的发展。

4) 社会资源的合理分配和共享

学校资源的平衡归根到底是社会资源的合理分配和共享。校际资源的平衡能在多方面优化甚至解决学生由于个人、家庭差异带来的负面影响。

我国不同地区的城市，经济发展差异悬殊，单凭地方财政实现教育公平难度巨大。希望国家能够给予适当的政策倾斜，将更多的公共资源投入到更贫困更边远的地区，慢慢缩小区域间差距。同理，各级政府也在配置资源时，应当有适当的倾斜，慢慢缩小城乡间的差距。

另外，部分学校的资源短缺情况也能通过共享方式来解决。首先对于优势院校，教师们通过输出优质的教学管理经验，形成共享的系统化资源；其次，需要加强共享资源的有效利用，一方面通过线上能够直接的输出到有需要的学校和学生，另一方面可通过线下的教师经验分享会。总之，我们可以根据需求，多方式地解决问题。