高层建筑外廊行人风环境研究

Study on Pedestrian Wind Environment in Out-Corridor of High-Rise Building

摘要: 为了研究高层建筑塔楼外廊区域的行人风环境，进行了一系列的数值模拟研究。研究结果表明，当来流风向与建筑面垂直时，外廊行人区域整体风速偏小，随着来流风向与建筑立面夹角的增大，塔楼外廊行人高度处风速逐渐增大，最大风速通常出现在外廊的拐角区域。随着外廊宽度增加，行人高度处的风速有所增大，随着外廊围栏高度的增加，外廊行人高度处的风速逐渐减小。最终考虑不同建筑尺寸，提出了塔楼外廊最大风速加速比的经验公式，可为高层建筑外廊的行人风环境评估提供参考。

Abstract: In order to study the pedestrian wind environment in the out-corridor of high-rise buildings, a series of CFD simulations were carried out. The results show that when the wind direction is perpendicular to the building surface, the wind speed in the pedestrian area of the outer corridor is relatively small, and gradually increases with the increase of wind direction angle. The maximum wind speed usually occurs in the corner area of the outer corridor. Meanwhile, the wind speed increases with the width of the corridor increases, and decreases with the height of the corridor fence. Considering different building sizes, an empirical formula for the maximum speed-up ratio of the out-corridor was proposed, which can provide reference for the assessment of pedestrian wind environment.

1. 引言

高层建筑附近区域的局部强风可能使行人行走困难，甚至造成行人被吹倒跌伤等安全事故，城市“峡谷风”是当今城市所面临的20种新城市灾害之一。近年来，一些超高层建筑设置了高空露台、外廊、屋顶等露天区域，以营造更多的室外活动空间。比如图1所示的超高层建筑，分别在四个高度设置的较大区域的室外走廊。当大风来临时，高空露天区域可能遭受局部强风，影响行人安全，对这些区域进行风环境研究具有重要现实意义。

Figure 1. A super high-rise building

图1. 某超高层建筑

行人风环境关系到行人安全性和舒适性，长期以来一直备受关注，诸多国内外学者基于实测、风洞试验和CFD数值模拟等手段进行了相关研究 ‎[1] - ‎[6] 。从既有研究来看，关于建筑周围地面行人高度处风场特性的研究已经相对成熟，对高空露天活动区域的行人风环境很少关注。根据平均风速剖面的沿高增长特性，高空区域的来流风速更大，造成的风环境问题可能更为突出。随着社会的发展，此类高空人员活动区域会更为常见。鉴于此，本文针对图1所示的一类建筑外廊，进行了一系列的数值模拟研究。

2. 数值模拟概况

以图1所示的高层建筑为原型，模型化的建筑情况如图2所示，塔楼高240米、宽40米，裙房宽160米。数值模拟工况如表1所示。

Figure 2. High-rise building model

图2. 高层建筑模型示意图

Table 1. Numerical simulation condition table of out-terrace

表1. 塔楼外廊风环境数值模拟工况表

根据塔楼实际尺寸，考虑数值模拟效率和精度，计算域尺寸定为H × D × L = 800 m × 1000 m × 2500 m，计算域如图3所示。采用适应性强的四面体网格(见图4)，并对建筑表面和围栏等区域进行加密，加密区域的最大网格尺寸为0.5 m，总网格数约为300万。

Figure 3. The set of calculate area

图3. 计算域设置

Figure 4. Building model meshing

图4. 建筑模型网格划分

湍流模型选择Realizable k-e模型，入口边界采用速度入口边界条件，计算域出流条件设置为自由出口，计算域顶面和两个侧面采用对称边界条件，模型表面和计算域底面采用无滑移壁面条件。风速剖面、湍动能k和湍流耗散率e等入口边界条件通过编写自定义函数(UDF)实现。求解方式为基于压力求解器(Pressure-Based)，求解模态为稳态求解(Steady)，选用SIMPLE算法求解。考虑收敛性和模拟精度，选用二阶离散格式，计算收敛的标准为无量纲残差达到1 × 10⁻⁴且保持稳定。

3. 模拟结果分析

3.1. 风速比和加速比的定义

在进行风环境评价时，业界常用方法之一是以平均风速比作为评价标准，计算公式为：

$R=\frac{V_r}{V_0}$ (1)

式中，V_r为监测区域的平均风速(m/s)；V₀为当地标准地貌10 m高度处的平均风速(m/s)。

为了使研究结果具有一般适用性，本文采用加速比的概念来衡量风速分布情况，将加速比定义为：

$R_{\infty }=\frac{V_r}{V_{\infty }}$ (2)

式中， $V_{\infty }$ 为监测区域所在高度的来流平均风速(m/s)。

加速比与风速比本质含义一致，仅参考高度不同。加速比参考点高度与监测区域高度相同，故而加速比与来流风速、地面粗糙度、裙房高度都无关。

3.2. 风向角的影响

为确定塔楼外廊行人风环境的最不利风向角以及风向角对风速分布的影响，首先进行不同风向角下的数值模拟分析，风向角的定义如图5所示。

Figure 5. Definition wind direction

图5. 风向角示意图

图6为不同风向角下塔楼外廊行人高度风速矢量云图。从图6来看：当来流方向与建筑立面垂直时，最大加速比出现在上游两拐角处；当来流方向与建筑立面接近45度时，最大加速比出现在侧向两拐角处；不论何种风向角，背风区域的风速整体较小。根据数值模拟结果，计算所得的各风向角下最大加速比见图7。从图7可以看出，外廊行人高度处最大加速比随着来流风向角的增大而逐渐增大。根据这一结果，将外廊设置在当地主导风向的下游背风区域，或将外廊避开建筑物的拐角区域对行人风环境的舒适性和安全性是有利的。

(a) 0度风向角 (b) 20度风向角(c) 30度风向角 (d) 45度风向角

Figure 6. Wind speed vector under different wind directions

图6. 不同风向角下塔楼外廊行人高度风速矢量图

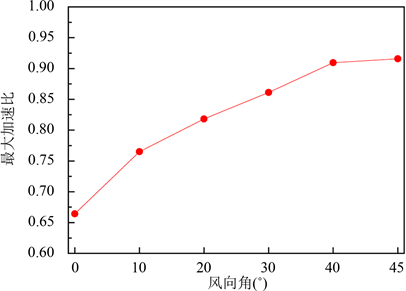
Figure 7. Maximum speed-up ratio under different wind directions

图7. 不同风向角下塔楼外廊最大加速比

3.3. 外廊宽度的影响

针对最不利风向角(45度)，本节研究外廊宽度对风环境的影响。图8为不同外廊宽度下的行人高度风速矢量图(部分工况)，图9为不同外廊宽度下的最大加速比。从图8和图9的结果来看，外廊最大加速比随着外廊宽度的增大而逐渐增大，当外廊宽度达到围栏高度的3倍时，最大加速度比将接近1.0。这是因为，当外廊宽度较小时，由于围栏的遮挡效应，使得外廊区域行人风速较小，当外廊宽度逐渐增大，遮挡效应减弱，行人风速逐渐变大。

(a) 外廊宽3 m (b) 外廊宽5 m(c) 外廊宽7 m (d) 外廊宽9 m

Figure 8. Wind speed vector under different out-terrace width

图8. 不同外廊宽度下行人高度风速矢量图

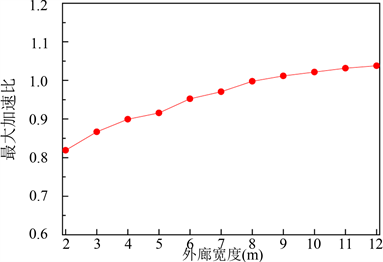
Figure 9. Max speed-up ratio under different out-terrace widths

图9. 不同外廊宽度下外廊最大加速比

3.4. 围栏高度的影响

(a) 无围栏 (b) 围栏高1.5 m(c) 围栏高2.5 m (d) 围栏高4.0 m

Figure 10. Wind speed vector under different fence heights

图10. 不同围栏高度下塔楼外廊风速矢量图

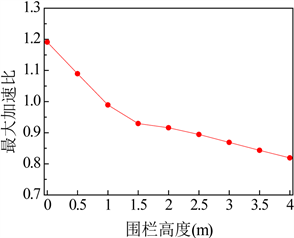
Figure 11. Max speed-up ratio under different fence heights

图11. 不同围栏高度下外廊最大加速比

图10为不同外廊围栏高度下的行人高度风速矢量图(部分工况)，图11为不同围栏高度下的最大加速比。从图10的结果来看，随着围栏高度的增加，加速区域面积逐渐减小，比如当围栏高度为1米时，高速区域几乎布满整个走廊，而当围栏高度达到3米时，高速区域仅出现在走廊内侧靠近建筑表面处。从图11的结果来看，外廊最大加速比随着围栏高度的增加而逐渐减小，造成这一现象的原因是围栏对对来流风的遮挡效应。

4. 最大加速比经验公式

根据上述不同工况的数值模拟结果，提出适合的塔楼外廊行人高度最大加速比的经验公式为：

$R_{\max }=0.226x_d+0.3518{\text{e}}^{-x_h}+0.7448$ (3)

式中，x_d为外廊宽度，x_h为外廊围栏高度。

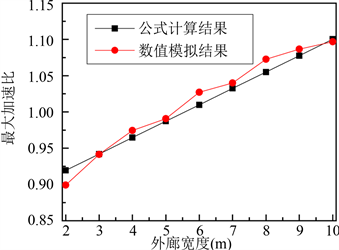
经验公式(3)计算结果与数值模拟结果的对比情况见图12。从图12的结果可以看出经验公式的结果与数值模拟结果比较吻合。

(a) 围栏高1 m (b) 外廊宽7 m

Figure 12. Comparison of CFD results and formula results

图12. 数值模拟结果与公式计算结果对比

本文加速比与来流风速、地面粗糙度、裙房高度无关，在实际应用时，需结合当地实际风剖面和监测区域的实际高度将加速比换算为风速比或实际风速值，即可进行风环境评价。当存在建筑群体干扰时，以受干扰后的风速作为来流风速，再结合式(3)即可用于群体建筑中裙房屋面的风环境评价。

5. 结论

本文在数值模拟计算的基础上，对高层建筑塔楼外廊行人风速分布特性进行了研究，得到不同建筑尺寸塔楼外廊行人高度处最大加速比的变化规律。主要结论如下：

1) 当来流方向与建筑立面垂直时，最大加速比出现在上游两拐角处；当来流方面与建筑立面接近45度时，最大加速比出现在两侧拐角处。外廊行人高度处最大加速比随着来流风向角的增大而逐渐增大。不论何种风向角，背风区域的风速整体较小。

2) 由于围栏的遮挡效应，当外廊宽度较小时，外廊区域行人风速较小，当外廊宽度逐渐增大，遮挡效应减弱，行人风速逐渐变大。外廊最大加速比随着外廊宽度的增大而逐渐增大，当外廊宽度达到围栏高度的3倍时，最大加速度比将接近1.0。随着围栏高度的增加，外廊最大加速比和加速区域面积均逐渐减小。

3) 在现有数值模拟结果基础上，考虑不同的建筑尺寸，提出塔楼外廊行人高度最大加速比和最大风速比的经验公式，可为高层建筑外廊的行人风环境评估提供参考。