一个关于材料力学例题的讨论

Discussions of an Example in Mechanics of Materials

摘要: 现行的许多材料力学教材中列举过一个两端固定的静不定梁在横向集中力作用下的挠度和约束力的计算实例，然而，在该例的分析和计算当中，却忽略了固定端轴向约束力的影响。本文在计入固定端轴向约束力影响的基础上，分析计算了该梁中点的挠度以及梁两端的约束力，并与材料力学教材中所给出的未计入固定端轴向约束力影响的对应结果进行了比较，发现两者之间存在显著差异，进而说明：在两端固定的静不定梁的挠度和约束力的分析计算当中，计入固定端轴向约束力的影响是完全必要的。

Abstract: There is an example of determining deflection and constraint forces of a statically indeterminate beam with two fixed ends subjected to transverse load in many textbooks on mechanics of materials. However, in this example, the influence of axial constraint forces at the fixed ends is not taken into consideration. In the present paper, taking into account the influence, the results of the deflection of the center point of the beam and constraint forces at the two fixed ends are determined. These results are found to be strikingly different from the corresponding results without accounting for the influence of axial constraint forces presented in textbooks on mechanics of materials. This indicates that the inclusion of the influence of axial constraint forces in determining deflection and constraint forces of statically indeterminate beams with two fixed ends subjected to transverse load is necessary.

1. 引言

材料力学教材 [1] - [10] 中列举过如下一个典型例题：如图1所示，一根长度为l、截面积为S、截面惯性矩为I、弹性模量为E的等截面直梁的两端被固定，梁的中部作用有横向集中力 $F$ ，试确定该梁中点的挠度和梁两端的约束力。值得注意的是：上述材料力学教材针对这一例题所给出的分析和求解答案当中，并没有计入固定端轴向约束力的影响。本文在计入固定端轴向约束力影响因素的基础上，通过分析计算出该梁中点的挠度和梁两端的约束力，并与上述材料力学教材中所给出的未计入固定端轴向约束力影响的对应结果进行比较，以说明在两端固定的静不定梁的挠度和约束力的分析计算当中考虑固定端轴向约束力影响的必要性。

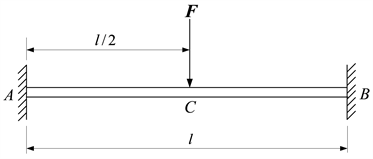
Figure 1. Statically indeterminate beam with two fixed ends

图1. 两端被固定的静不定梁

2. 挠曲线微积分方程

下面研究如图1所示的两端固定的静不定梁的挠度和约束力计算问题，为此首先画出该梁的受力图——图2，注意图中除了标出A、B两端的剪力和弯矩外，还标出这两端的轴向约束力 $F_{Ax}$ 和 $F_{Bx}$ (梁发生弯曲变形后，梁的长度会有所增加，因而在梁的两端必然存在轴向拉力)。

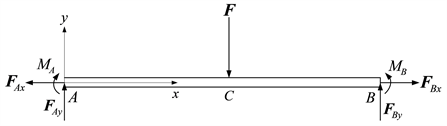
Figure 2. The forces acting on the beam

图2. 作用在梁上的力

根据静力学平衡方程 ${\displaystyle \sum F_y}=0$ ，列写出

$F_{Ay}-F+F_{By}=0$ (1)

进一步根据对称性原理，可知

$F_{Ay}=F_{By}$ (2)

联立以上两个方程，解得

$F_{Ay}=F_{By}=\frac{1}{2}F$ (3)

注意：这里完全根据静力学平衡方程和对称性原理无法求出 $F_{Ax}$ 、 $F_{Bx}$ 、 $M_A$ 和 $M_B$ ，这四个未知量将在求出梁的挠曲线函数后才能被进一步求出。

下面接着研究该梁的挠曲线。考虑到该梁的左半段挠曲线和右半段挠曲线是对称的，因此只需研究该梁的左半段挠曲线即可。为此应用截面法，取横坐标为x ( $0\le x\le l/2$ )的横截面的左侧截断梁为研究对象，画出该截断梁处于变形位置时的受力图——图3，图中的 $F_{\text{N}}\left(x\right)$ 、 $F_{\text{S}}\left(x\right)$ 和 $M\left(x\right)$ 分别表示横坐标为x处的横截面上分布的轴力、剪力和弯矩(图中的轴力、剪力和弯矩均按正方向画出)， $w\left(x\right)$ 表示此截面的挠度。由该截断梁的力矩平衡方程，容易推导出弯矩 $M\left(x\right)$ 的表达式如下式(4)。

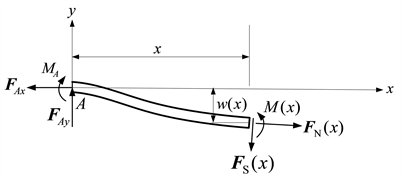
Figure 3. Free-body diagram of a section beam on the left of the cross section of abscissa x

图3. 横坐标为x的横截面的左侧截断梁在变形位置的受力图

$M\left(x\right)=M_A+F_{Ay}x+\underset{\_}{F_{Ax}w\left(x\right)}$ ( $0\le x\le l/2$ )(4)

上式中的画线项 $F_{Ax}w\left(x\right)$ 代表固定端的轴向约束力 $F_{Ax}$ 对于弯矩函数的贡献，这里需要说明的是只有将截断梁的变形位置(图3)作为平衡位置分析，才能在弯矩函数 $M\left(x\right)$ 中计入该轴向约束力的贡献。

将式(4)代入梁的挠曲线近似微分方程 $EI{w}^{″}\left(x\right)=M\left(x\right)$ 后，得到

$EI{w}^{″}\left(x\right)=M_A+F_{Ay}x+F_{Ax}w\left(x\right)$ ( $0\le x\le l/2$ ) (5)

根据胡克定律，轴向约束力 $F_{Ax}$ 和该梁中部截面上的轴力 $F_{Cx}$ 可写为

$F_{Ax}=F_{Cx}=k_{AC}\cdot \text{Δ}{l}_{AC}$ (6)

式中， $k_{AC}$ 和 $\text{Δ}{l}_{AC}$ 分别为梁的左半段(AC段)的拉压刚度和该段梁的伸长量，其表达式分别为

$k_{AC}=\frac{ES}{l/2}$ (7)

和

$\text{Δ}{l}_{AC}={\displaystyle {\int }_0^{l/2}\sqrt{1+{\left[w^{\prime }\left(x\right)\right]}^2}}\text{d}x-l/2\approx {\displaystyle {\int }_0^{l/2}\left\{1+\frac{1}{2}{\left[w^{\prime }\left(x\right)\right]}^2\right\}\text{d}x}-l/2=\frac{1}{2}{\displaystyle {\int }_0^{l/2}{\left[w^{\prime }\left(x\right)\right]}^2\text{d}x}$ (8)

将以上两式代入式(6)后，得到

$F_{Ax}=\frac{ES}{l}{\displaystyle {\int }_0^{l/2}{\left[w^{\prime }\left(x\right)\right]}^2\text{d}x}$ (9)

根据梁的挠曲线近似微分方程 $EI{w}^{″}\left(x\right)=M\left(x\right)$ ，可以将该梁在固定端A处的弯矩表达为

$M_A=M\left(0\right)=EI{w}^{″}\left(0\right)$ (10)

将式(3)、式(9)和式(10)代入式(5)后，得到

$EI{w}^{″}\left(x\right)=EI{w}^{″}\left(0\right)+\frac{1}{2}Fx+\frac{ES}{l}w\left(x\right){\displaystyle {\int }_0^{l/2}{\left[w^{\prime }\left(x\right)\right]}^2\text{d}x}$ ( $0\le x\le l/2$ ) (11)

这就是左半段梁(AC段)的挠曲线微积分方程。左半段梁的边界条件为

$w\left(0\right)=0$ , $w^{\prime }\left(0\right)=0$ , $w^{\prime }\left(l/2\right)=0$ (12)

3. 挠曲线函数

下面应用瑞利–里兹法 [11] 求方程(11)且满足边界条件(12)的近似解析解。为此，选取满足边界条件(12)的以下两个函数

$w_1\left(x\right)=x^4-2l{x}^3+l^2{x}^2$ (13)

和

$w_2\left(x\right)=x^6-3l{x}^5+2l^2{x}^4+l^3{x}^3-l^4{x}^2$ (14)

作为瑞利–里兹函数，于是可以将左半段梁(AC段)的挠曲线函数表达为

$w\left(x\right)=c_1{w}_1\left(x\right)+c_2{w}_2\left(x\right)$ ( $0\le x\le l/2$ ) (15)

式中的两个待定未知量 $c_1$ 和 $c_2$ 可按如下的方法确定：将式(15)代入方程(11)，然后在方程的两边乘以 $w_i\left(x\right)\left(i=1,2\right)$ ，再将所得到的方程的两端分别作为被积函数取定积分 ${\displaystyle {\int }_0^{l/2}\left(\right)\text{d}x}$ ，然后再经过化简得到如下两个关于 $c_1$ 和 $c_2$ 的非线性代数方程：

$\begin{array}{l}\text{7744}ES{l}^9{c}_1^3-\text{28864}ES{l}^{11}{c}_1^2{c}_2+\text{35904}ES{l}^{13}{c}_1{c}_2^2+\text{43908480}EIl{c}_1-\text{14904}ES{l}^{15}{c}_2^3\\ -\text{46347840}EI{l}^3{c}_2+\text{2934855}F=0\end{array}$ (16)

$\begin{array}{l}\text{1976832}ES{l}^9{c}_1^3-\text{7369472}ES{l}^{11}{c}_1^2{c}_2+\text{9168512}ES{l}^{13}{c}_1{c}_2^2+\text{11162511360}EIl{c}_1\\ -\text{3806592}ES{l}^{15}{c}_2^3-\text{11808276480}EI{l}^3{c}_2+\text{748692945}F=0\end{array}$ (17)

设梁的长度 $l=1\text{m}$ ，横截面积 $S=6\times {10}^{-5}{\text{m}}^{\text{2}}$ ，截面惯性矩 $I=4.5\times {10}^{-11}{\text{m}}^{\text{4}}$ ，弹性模量 $E=2.01\times {10}^{11}\text{Pa}$ ，作用在梁中部的横向集中力 $F=25\text{N}$ 。将上述已知数据代入方程(16)和(17)后，应用MATLAB Solve [12] 求解该组方程，得到其实数解(舍去非实数解)为 $c_1=-0.0162{\text{m}}^{-3}$ 和 $c_2=0.0504{\text{m}}^{-5}$ ，最后将此解以及式(13)和式(14)代入式(15)，得到

$w=x^2{\left(x-1\right)}^2\left(0.0504x^2-0.0504x-0.0666\right)\left(\text{m}\right)$ (18)

式(18)就是在计入固定端轴向约束力影响的情况下得到的左半段梁的挠曲线函数(右半段梁的挠曲线同左半段梁的挠曲线相对称，所以无需再求解右半段梁的挠曲线函数)。

4. 计算结果及比较讨论

由挠曲线函数(18)可计算出梁中点的挠度

$w_C={w|}_{x=0.5}=-0.0050\left(\text{m}\right)$ (19)

由此进一步可知梁中点挠度的绝对值与梁的跨度之比 $\frac{\left|w_C\right|}{l}=0.5\%$ ，这说明该梁的变形属于小变形情形。

将式(18)和梁的已知参数代入式(9)后，计算得到固定端A的轴向约束力为

$F_{Ax}=722.1152\left(\text{N}\right)$ (20)

该结果说明：即使在梁的小变形情形下，也不能笼统地认为该梁固定端的轴向约束力为零或近似为零。

固定端A的剪力(固定端A的横向约束力)由式(3)给出，并由此式计算得到

$F_{Ay}=\frac{1}{2}F=12.5\left(\text{N}\right)$ (21)

将式(18)和梁的已知参数代入式(10)后，计算得到固定端A的弯矩为

$M_A=-1.2048\left(\text{N}\cdot \text{m}\right)$ (22)

在求出上述固定端A的约束力的基础上，可进一步根据对称性原理求得固定端B端的约束力(从略)。

到此为止，在考虑固定端轴向约束力影响的情形下分别求出了梁中点的挠度和固定端的约束力。为了将这些结果同未考虑固定端轴向约束力影响的对应结果进行比较，下面将材料力学教材 [1] - [10] 中所给出的未计入固定端轴向约束力影响的该梁中点的挠度和固定端约束力的表达式以及应用这些表达式所得到的计算结果列写如下：

$w_C^{*}=-\frac{F{l}^3}{192EI}=-0.0144\left(\text{m}\right)$ (23)

$F_{Ax}^{*}=F_{Bx}^{*}=0$ (24)

$F_{Ay}^{*}=F_{By}^{*}=\frac{1}{2}F=12.5\left(\text{N}\right)$ (25)

$M_A^{*}=M_B^{*}=-\frac{Fl}{8}=-3.125\left(\text{N}\cdot \text{m}\right)$ (26)

分别将式(19)~式(22)给出的结果同式(23)~式(26)给出的结果进行比较，可以发现：① 在计入固定端轴向约束力影响的情形下求得的梁中点挠度的绝对值远小于未计入固定端轴向约束力影响的情形下所求得的梁中点挠度的绝对值，后者对前者的相对误差竟高达188%；② 在计入固定端轴向约束力影响的情形下求得的固定端轴向约束力远大于零，因此，即使在该梁的小变形条件下也不能认为“固定端的轴向约束力为零或近似为零”；③ 在计入与不计入不固定端轴向约束力影响的两种情形下所求得的固定端剪力(固定端的横向约束力)是相同的；④ 在计入固定端轴向约束力影响的情形下所求得的固定端弯矩的绝对值明显小于未计入固定端轴向约束力影响的情形下所求得的固定端弯矩的绝对值，后者对前者的相对误差竟高达159%。上述几点说明：在两端固定的静不定梁的挠度和约束力的分析和计算当中，计入固定端轴向约束力的影响是完全必要的，否则会造成较大的计算误差，甚至会出现错误的计算结果。

5. 结束语

本文针对一些材料力学教材中列举过的两端固定的静不定梁在横向集中力作用下的挠度和约束力的计算实例进行了研究，研究当中考虑了材料力学教材中未曾考虑过的固定端轴向约束力的影响，给出了计入固定端轴向约束力影响的梁中点的挠度以及梁两端约束力的计算结果，在此基础上，与材料力学教材中给出的未计入固定端轴向约束力影响的对应结果就行了比较，发现后者的结果明显不同于前者，进而说明：在两端固定的静不定梁的挠度和约束力的分析和计算当中，计入固定端轴向约束力的影响是完全必要的。