1. 引言
降落伞具有质量轻、减速效果好的优点,在航空航天领域内得到了广泛应用,包括无人机回收、载人航天器返回等气动减速任务 [1] 。降落伞依靠在空气中产生气动阻力实现减速制动,附近流体具有的动量发生变化后会使得降落伞受到额外的惯性阻力,附加质量被用来直观地描述该惯性力 [2] 。由于降落伞是一个大而轻薄又有着巨大容积的物体,因而在空气中运动时伞衣内部携带着大量气体,且总质量远远超过降落伞本身,特别是在充气展开过程中,伞衣的形状、尺寸和体积变化十分激烈,流固耦合效应显著,降落伞附加质量及其变化也因此非常复杂又非常剧烈,对其动力学特性产生了重大影响。一般降落伞附加质量的确定主要依赖试验和工程经验进行估算,且往往将其视为伞衣体积或是阻力面积的函数 [3] - [8] ,而降落伞充气过程中的伞衣体积和阻力面积又难以准确得到,一些简化假设导致附加质量的计算结果与实际情况存在较大偏差 [9] ,最终影响降落伞开伞载荷计算分析的准确性。随着计算机技术和数值仿真技术的发展,目前已能通过数值仿真的方式获取降落伞充气展开过程中的伞衣外形变化 [10] [11] [12] [13] ,并且仿真结果的精度也在可接受范围内,这为降落伞充气时的伞衣体积和阻力面积计算提供了一条新的技术途径。
本文通过数值仿真的方式模拟了降落伞的充气展开过程,从仿真结果中获取到降落伞充气时的伞衣体积和阻力面积变化规律,然后针对常用的降落伞附加质量工程计算方法,分析了附加质量对降落伞开伞载荷的影响。
2. 物伞系统动力学模型分析
动力学分析是降落伞常用的气动性能研究方法,根据不同程度的简化可以建立多个不同的物伞系统运动方程组 [14] ,其中二自由度平面动力学模型较为简单,可直接计算得到降落伞开伞载荷和物伞系统运动速度等,且精度能够满足一般的分析需求,因此,为了便于问题分析,本文使用该模型计算分析附加质量对降落伞开伞载荷的影响。
如图1所示,为物伞系统平面动力学分析模型。图中t为时间;Fk为降落伞开伞载荷;v为物伞系统运动速度;θ为物伞系统弹道倾角;ρ为气体密度;gn为重力加速度;A为伞衣阻力面积;Aw为进入器阻力面积;ms为降落伞质量;mw为进入器质量;mf为附加质量。
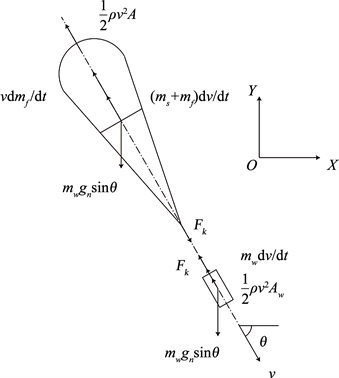
Figure 1. Plane dynamics analysis model of forebody-parachute system
图1. 物伞系统平面动力学分析模型
物伞系统平面动力学分析模型的基本假设如下 [15] :
1) 物伞系统为双质点系统,且质心分别位于进入器的重心和降落伞伞衣底边中心处;
2) 物伞系统始终保持在二维平面内运动;
3) 物伞系统的运动轴线始终重合;
4) 忽略物伞之间伞绳弹性的影响。
根据充气时间法求解该模型的微分方程为:
(1)
由上述Fk的计算表达式可知,开伞载荷包括惯性力、伞衣阻力、附加质量变化引起的反作用力以及降落伞重力。一般附加质量大小是降落伞质量的数倍以上,导致惯性力中附加质量的占比较大,此外附加质量变化率与物伞系统运动速度的乘积可以是比较大的数值,因此附加质量对降落伞气动性能的影响不容忽视。
3. 降落伞附加质量计算方法
3.1. 基于阻力面积的计算方法
附加质量计算是流体力学研究中的难点,结构复杂的物体其附加质量没有解析解,工程中通常根据降落伞阻力面积的变化规律计算分析其附加质量 [16] [17] ,如式(2)所示。
(2)
式中:kA为修正系数。
采用该方法需要事先获取降落伞充气过程中的阻力面积变化规律,且式(2)中A1.5的本质是用阻力面积模拟得到降落伞体积来计算附加质量。
3.2. 基于体积的计算方法
根据降落伞与流体相互作用的特点,可将附加质量分解为内含质量和表观质量来计算 [18] [19] :内含质量可由伞衣体积与气体密度直接计算得到;表观质量是伞衣外部随动的气体质量,其大小难以描述,但是任意状态下降落伞的表观质量与内含质量之比是存在的,被称为表观质量系数,因此降落伞附加质量还可以通过式(3)进行计算:
(3)
式中:V为伞衣体积;kf为表观质量系数。
使用该方法需要已知充气过程中的伞衣体积变化规律。另外,文献 [20] 研究指出表观质量系数是随时间而变化的,并且与时间是单值函数关系。
3.3. 基于椭球体势流理论的计算方法
根据势流理论,椭球体的附加质量可由式(4)计算 [21] :
(4)
式中:a和b为椭圆的赤道半径,c为椭圆的半长轴;α所在项表征了椭球体沿其对称轴运动的表观质量。根据文献 [21] α的取值接近1,将α = 1代入式(4)得到:
(5)
该方法将充满的伞衣视为椭球体,若用伞衣体积V表示其中的椭球体积
,则式(5)与式(3)便具
有相同的形式,进一步得到α取1与kf取1是等价的。
3.4. 附加质量工程计算方法
根据分析,不同降落伞附加质量计算方法的差异性在于附加质量系数的确定以及伞衣体积获取方式,由此本文确定出三种降落伞附加质量计算方法,如表1所示。根据2.3小节,kf可取定值1,即方法2;同时为了避免附加质量大小的不确定性影响分析结果,附加质量计算公式中的修正系数大小应使得在降落伞稳态阶段的附加质量计算结果尽量接近,因此以方法2为参照不断调整可得到kA,即方法1;最后,根据文献 [21] 的内容考虑令kf按照某种规律变化增大,即方法3,但是变化的kf取值下限不能过小也不能与上限十分接近,因此综合考虑之下确定kf的变化范围为[0.5, 1.0]。

Table 1. Engineering calculation methods of parachute added mass
表1. 降落伞附加质量工程计算方法
4. 降落伞充气过程数值仿真
为了获得降落伞充气过程中的形状和体积变化规律,以及伞衣阻力面积变化规律,用于表1所示附加质量的计算和动力学模型分析,对降落伞的充气过程进行了数值模拟。
4.1. 仿真模型
本文以某型号环帆伞为研究对象,主要尺寸参数如表2所示,伞衣幅结构如图2所示,其中伞衣幅总长h为3970 mm,上宽la为52 mm,下宽lb为989 mm;环高hr为1640 mm;帆高hs为2250 mm;环缝宽度r为40 mm。

Table 2. Parachute main structural dimensions
表2. 降落伞主要结构尺寸
为了确保仿真中降落伞开伞充气时的初始状态与空投试验一致,本文在仿真模型中添加了收口绳结构并采用单元失效的方式实现收口控制,如图3(a)所示,由于仿真设置的关系,收口绳使用了2D网格单元。仿真时首先维持收口状态计算一段时间,直到降落伞与流场达到稳定,然后才解除收口进行充气展开计算,从而使得仿真模型在开伞时刻的状态与实际情况相符,保证开伞充气仿真数据的合理性。
如图3(b)所示,记D0为降落伞名义直径,则流场仿真模型是直径为4D0、高度为5D0的圆柱形流场。为了使得仿真模型能够捕捉降落伞最小结构孔隙的气体流动,以保证开伞载荷、开伞时间以及伞衣外形变化等仿真结果的正确性,对伞衣附近的流场网格进行了局部加密。
另外,根据该伞某次空投试验中解除收口时的环境条件,得到仿真计算初始条件如表3所示。
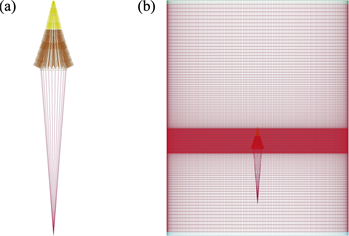
Figure 3. Simulation model: (a) Parachute model; (b) Fluid model
图3. 数值仿真模型:(a) 降落伞仿真模型;(b) 流场仿真模型

Table 3. Simulation initial conditions
表3. 仿真初始条件
4.2. 仿真结果及数据处理
仿真中解除收口时刻所得伞衣外形与风洞试验中的伞衣外形比较如图4所示,可以看出仿真模型在收口绳约束下的状态与实际情况是一致的,同时收口稳定状态以及伞衣充满稳定状态的阻力面积与空投试验的对比如表4所示,二者误差小于2%,因此仿真结果是可靠的。
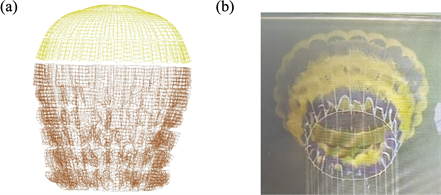
Figure 4. Comparison of parachute reefed canopy shape: (a) Reefed ca nopy shape in simulation; (b) Reefed canopy shape in wind tunnel test
图4. 降落伞收口状态伞衣外形对比:(a) 数值模拟伞衣收口外形; (b) 风洞试验伞衣收口外形

Table 4. Comparison of canopy drag area
表4. 伞衣阻力面积对比
根据仿真结果提取伞衣节点坐标数据,通过数值积分的方式计算得到了仿真模型在解除收口后的伞衣投影面积S和伞衣体积V [22] 变化曲线,如图5所示,曲线的时间零点被设定为解除收口时刻。根据图5(a)伞衣投影面积第一次达到稳态平均值24.74 m2的时间得到仿真模型伞衣充满时间tf为0.5324 s。
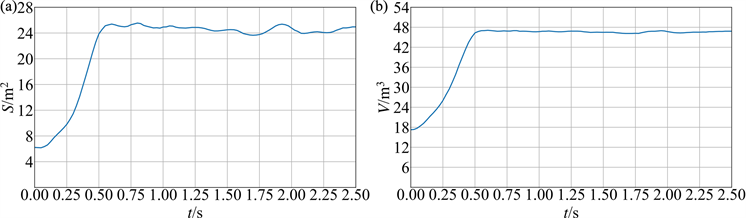
Figure 5. Curves of canopy projected area and volume in simulation: (a) Canopy projection area curve; (b) Canopy volume curve
图5. 仿真伞衣投影面积与体积变化曲线:(a) 伞衣投影面积曲线;(b) 伞衣体积曲线
考虑到降落伞附加质量计算方法1以及通过式(1)分析降落伞开伞载荷需要已知充气过程中的伞衣阻力面积,表4中已获得阻力面积的变化范围,为此假设降落伞阻力面积的变化规律与其投影面积变化规律相同 [23] ,并由式(6)计算得到阻力面积曲线:
(6)
式中:
为稳态阻力面积;Ad为收口稳定状态下的伞衣阻力面积;Sd为收口稳定状态下的伞衣投影面积;St为某时刻伞衣投影面积;
为伞衣稳态投影面积。
为了更直观地理解充气过程中降落伞阻力特性的变化规律,以及后续分析使用,将所得阻力面积曲线处理为无量纲充气时间 的形式,如图6所示,其中 的定义为:

Figure 6. Curve of parachute resistance area with T
图6. 降落伞阻力面积随T变化曲线
5. 附加质量对降落伞开伞载荷的影响
5.1. 附加质量及其变化率
根据表1所示三种附加质量计算方法,利用相应仿真数据,计算得到了降落伞附加质量曲线,如图7(a)所示,同样将其处理成了 的形式。对图7(a)曲线求导,便得到图7(b)所示附加质量变化率
曲线,
其中曲线峰值大小以及峰值时间如表5所示。

Figure 7. Dimensionless inflation time curves of parachute added mass and change rate: (a) Curve of added mass with T; (b) Curve of added mass change rate with T
图7. 降落伞附加质量及其变化率无量纲充气时间曲线:(a) 附加质量随T变化曲线;(b) 附加质量变化率随T变化曲线

Table 5. Peak value and dimensionless time of added mass change rates
表5. 附加质量变化率峰值及峰值无量纲时间
5.2. 开伞载荷计算
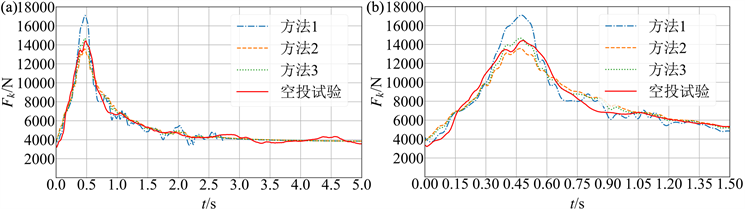
Figure 8. Comparison of prediction results of parachute opening load: (a) Opening loads during 0.0 s~5.0 s; (b) Opening loads during 0.0 s~1.5 s
图8. 开伞载荷预测结果对比:(a) 开伞载荷曲线(0.0 s~5.0 s);(b) 开伞载荷曲线(0.0 s~1.5 s)
由该伞空投试验的分析结果可知,其解除收口后的伞衣实际充满时间tf为0.58 s,进一步根据图6与图7(a)降落伞阻力面积与附加质量无量纲充气时间曲线,近似得到空投试验中降落伞充气时的阻力面积和附加质量变化规律,然后由式(1)动力学模型以及空投试验中该伞解除收口时刻的物理条件,计算得到了不同附加质量计算方法下的开伞载荷曲线,与空投试验载荷结果的对比如图8所示,其中开伞载荷峰值大小及峰值时间的对比如表6所示。

Table 6. Comparison of opening loads peak value and peak time
表6. 开伞载荷峰值及峰值时间对比
上述结果中,基于阻力面积的附加质量计算工程方法1得到的开伞载荷与空投试验相差较大,其载荷峰值误差达到了约18%,而基于体积的附加质量工程计算方法2、3得到的开伞载荷曲线在变化趋势上均与空投试验数据吻合较好,且载荷峰值大小和峰值时间的误差较小,处于可接受的范围内。
综上,在分析降落伞开伞载荷时附加质量的计算可以从内含质量和表观质量两部分来考虑,且假定表观质量系数按照伞衣投影面积变化规律而增大可以取得较好的分析结果,若投影面积变化规律未知或难以确定,也可简单地令表观质量与内含质量保持相等来分析。
5.3. 附加质量对开伞载荷的影响分析
为了进一步分析附加质量对降落伞开伞载荷的影响,如图9所示,忽略降落伞重力并将图8三种附
加质量计算方法所得开伞载荷Fk分解为惯性力
(用FI表示)、伞衣阻力
(用qA表示)以及附加质量变化引起的反作用力
三个部分。

Figure 9. Decomposition of opening loads: (a) Method 1; (b) Method 2; (c) Method 3
图9. 开伞载荷分解:(a) 方法1;(b) 方法2;(c) 方法3
根据图9,虽然伞衣阻力大小与开伞载荷大小比较接近,但是附加质量变化引起的反作用力对开伞载荷曲线的变化趋势更有决定性影响。结合表5与表6,可以看出附加质量变化率峰值过大或过小,开伞载荷峰值都会随之发生相同的变化,表明附加质量变化率特别是其峰值大小对降落伞开伞载荷分析的准确度具有较大影响。
为了进一步分析图9中曲线变化的规律,如表7所示,将开伞载荷Fk、附加质量变化率
及伞衣阻力qA的峰值时间进行了对比。其中,开伞载荷预测效果较好的方法3所得Fk峰值时间与
峰值时
间非常接近,而与qA峰值时间的间隔较长,表明附加质量变化率也是影响开伞载荷峰值出现时刻的重要因素。
另外,表7中方法1与方法3的
峰值时间均与其Fk峰值时间非常接近,结合表5与图9(a)表明方法1较大的
峰值是其开伞载荷预测结果偏大的主要原因;同时表7中方法2与方法3表明,较早出现的
峰值是方法2开伞载荷预测结果偏低的主要原因,因此如图9所示,加大
与qA之间峰值时间的差距是降低降落伞开伞载荷的一种有效途径。

Table 7. Comparison of peak times between Fk, d m f d t and qA
表7. Fk、
和qA的峰值时间对比
最后,从降落伞充气过程中伞衣结构变形与受力关系方面,可以为表7方法3中峰值时间前后规律的形成提供合理解释:
1) 在临近降落伞充满时刻,由于伞衣结构受限其织物内应力迅速增加,并在一瞬间内限制了伞衣的膨胀过程,因此与伞衣体积变化密切相关的附加质量其增加速度即附加质量变化率迅速减小,并在伞衣充满之前形成峰值;
2) 由于伞衣具有柔性,允许其在结构受限后继续延展,在伞衣充满后出现过充,导致伞衣投影面积仍然继续增加使得伞衣阻力面积增大,但是过充增加的伞衣阻力是有限的,伴随着充气过程中较大的阻力物伞系统运动速度在不断下降,导致动压持续降低,伞衣阻力转而降低并在伞衣充满后形成峰值;
3) 当附加质量变化率达到峰值后,其引起的反作用力载荷减小的速度非常快,虽然在过充阶段伞衣阻力几乎仍然在增加,但是不足以弥补载荷损失,受此影响开伞载荷出现峰值,并介于二者之间,且与附加质量变化率峰值时间十分接近。
6. 结论
本文用数值仿真的方式模拟了降落伞的充气展开过程,从中获得了降落伞充气时的形状、体积和阻力面积变化规律,然后针对降落伞常用的几种附加质量工程计算方法,使用物伞动力学模型比较分析了附加质量对降落伞开伞载荷的影响,并得出以下结论:
1) 附加质量工程计算方法对降落伞的开伞载荷分析具有较重要的影响,采用基于伞衣体积的方法计算降落伞的附加质量比较合适,其中表观质量系数按照伞衣投影面积变化规律而增大,且当伞衣充满后表观质量系数取1时可达到较高的分析精度;同时,表观质量系数直接取定值1也可以得到比较不错的分析结果。
2) 伞衣阻力与附加质量变化引起的反作用力是降落伞开伞载荷的主要来源,所研究降落伞开伞载荷构成中,二者比例接近2:1,因而分析降落伞气动性能特别是充气性能时不能忽略附加质量带来的影响。
3) 附加质量变化率是影响开伞载荷峰值大小及峰值出现时刻的主要因素,开伞载荷峰值时间一般在附加质量变化率峰值时间之后,且二者非常接近。
基金项目
飞行器环境控制与生命保障工业和信息化部重点实验室开放课题资助(KLAECLS-E-202004)。
NOTES
*通讯作者。