基于时间序列分析的广东省GDP的预测

The Forecast of GDP in Guangdong Province Based on Time Series Analysis

摘要: GDP是衡量一个国家或地区经济状况和发展水平的重要指标。因此，我们运用时间序列的方法对GDP变化作出预测是十分有意义的。在本文中，我们研究了ARIMA模型、指数平滑模型和方差倒数法组合预测模型三种模型对广东省2018~2021年GDP的预测效果。结果发现Holt两参数指数平滑模型的预测精度优于方差倒数法组合预测模型，组合预测模型优于ARIMA模型。

Abstract: GDP is an important indicator for measuring the economic status and development level of a country or region. Therefore, it is very meaningful for us to use the time series method to predict changes in GDP. In this article, we studied the predictive effects of three models, ARIMA model, exponential smoothing model, and reciprocal variance method combination prediction model, on the GDP of Guangdong Province from 2018 to 2021. The results showed that the prediction accuracy of the Holt two-parameter exponential smoothing model was superior to the reciprocal variance combined prediction model, and the combined prediction model was superior to the ARIMA model.

1. 引言

GDP是判断宏观经济运行状况的一个重要指标，同时也是政府制定经济发展战略的重要依据。广东省的经济一直保持迅猛发展，且其经济发展状况可以代表中国一线城市和新一线城市的发展水平。对广东省GDP进行有效地分析预测对于研究其经济水平有着重大意义。

近年来，国内外学者们从各个不同角度对GDP预测进行了研究。许多学者在预测精度要求不高时会选择经典的时间序列方法对GDP进行预测。严彦文 [1] 对1975~2015年山东省GDP进行分析，运用统计学原理，建立了ARIMA(1,1,1)模型，实验结果表明ARIMA(1,1,1)型有良好的预测效果。范恒瑞等 [2] 使用ARIMA模型与指数平滑法对江苏省未来若干年的GDP进行了预测，结果显示两种方法在较长的时间内预测结果有较大差别，但ARIMA模型在近期预测中效果较好。随着研究的逐步加深，越来越多研究者发现经典模型在理论和应用上存在很多局限性。在人们锲而不舍地研究下，时间序列分析在多变量、异方差、非线性等条件下取得了前所未有的进展。渐渐地，更多的GARCH族模型出现在人们的视野中。王丹和冯长焕 [3] 用HP滤波法将我国GDP序列分解成趋势序列和循环序列，由GDP序列减去预测的循环序列得到新的趋势序列并对其建立ARIMA-ARCH预测模型，与直接对GDP序列进行建模的预测结果进行比较，该方法的预测结果精度更高，验证了其可行性。此外，也有学者将ARIMA模型与BP神经网络进行组合来构建组合预测模型。莫东序 [4] 在广西的GDP预测中，利用ARIMA-BP神经网络混合预测，从预测结果看，混合模型的预测值优于应用单一的时间序列模型的预测值。

多数学者对于GDP的预测在预测精度要求不高时较多选择经典时间序列方法，由于此类传统方法操作方便，且具备较高的准确度能在一定程度上满足人们的预测目的。因此，本文以广东省GDP数据集为例，利用ARIMA模型和指数平滑模型建立单项预测模型，并在两项单项预测模型基础上建立方差倒数法组合预测模型，根据MAPE、SSE、RMSE和Theil IC四项指标，探讨出预测效果最好的模型用于广东省GDP的预测。

2. 广东省GDP的分级预测

2.1. 基于ARIMA模型的广东省GDP预测

2.1.1. 数据选取

本文采用广东省1978~2021年44年的GDP历史数据作为样本观测值，其中以1978~2017年GDP数据为训练集，以2018~2021年GDP数据为测试集。

2.1.2. 数据的平稳性检验及处理

对广东省1978~2017年GDP共40个数据绘制时序图，如图1所示。时序图蕴含显著的线性递增趋势，说明该序列非平稳，因此我们需对其进行差分处理，使非平稳时间序列转化成平稳的。先进行一阶差分处理，一阶差分后的序列(如图2所示)在波动中有上升趋势，表示序列未达到平稳状态。为使序列达到平稳状态，我们在此基础上继续对一阶差分后时间序列做差分处理得到二阶差分后时序图，如图2所示。

Figure 1. GDP time series of Guangdong Province from 1978 to 2017

图1. 广东省1978~2017年GDP时序图

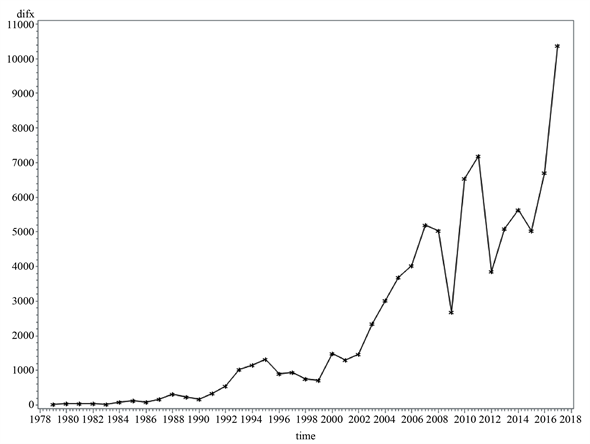
Figure 2. Time series of Guangdong Province’s GDP after first and second order difference from 1978 to 2017

图2. 广东省1978~2017年GDP一阶、二阶差分后时序图

二阶差分后的序列基本围绕在0值附近波动，此时已经没有明显的趋势特征，因此我们可以认为二阶差分后的序列是平稳的。为验证二阶差分后的时间序列是否真正达到平稳状态，我们需要继续对其进行ADF平稳性检验，结果如表1所示。

Table 1. Stationary test results of Guangdong Province’s GDP second-order difference series from 1978 to 2017

表1. 广东省1978~2017年GDP二阶差分后序列平稳性检验结果

ADF检验结果显示，二阶差分后序列的所有ADF检验统计量的P值全部小于0.05，因此我们可以确认实现了平稳。下面我们应该继续对二阶差分后的序列做白噪声检验，结果如表2所示。

Table 2. White noise test results of the second order difference series of GDP in Guangdong Province from 1978 to 2017

表2. 广东省1978~2017年GDP二阶差分后序列白噪声检验结果

表2显示延迟6阶、12阶、18阶的LB统计量的P值小于0.05，则拒绝原假设，认为二阶差分后的序列为非白噪声序列，也就是说二阶差分后的序列是平稳的非白噪声序列。

2.1.3. ARIMA模型定阶

图3显示延迟2阶、3阶自相关系数大于2倍标准差，延迟2阶、3阶的偏自相关系数大于2倍标准差。因此，首先尝试构建疏系数模型ARIMA((2,3),2,(2,3))，接着根据模型和各参数检验结果调整系数。最后，在通过参数检验和残差白噪声检验的所有模型中，ARIMA(0,2,(2,3))去除常数项后模型的AIC和BIC信息量同时达到最小。因此，我们选取ARIMA(0,2,(2,3))去除常数项后的模型为广东省GDP的拟合模型，拟合模型的形式为：

${\nabla }^2{X}_t=\left(1-0.49682B^2+0.50318B^3\right){\epsilon }_t,{\epsilon }_t~NID\left(0,951752.7\right)$

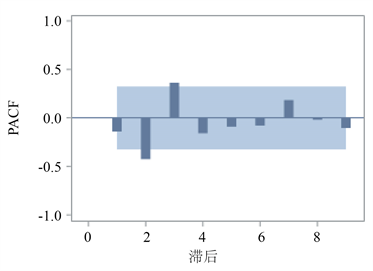
Figure 3. Sequential auto-correlation and partial auto-correlation of GDP after second-order difference in Guangdong Province from 1978 to 2017

图3. 广东省1978~2017年GDP二阶差分后序列自相关图、偏自相关图

2.1.4. ARIMA模型白噪声检验

表3显示在各延迟阶数下，所有P值均大于0.05，则我们可认为ARIMA(0,2,(2,3))去除常数项后模型通过了残差白噪声检验，即该模型显著成立。

2.1.5. ARIMA模型预测

我们借助ARIMA拟合模型，对广东省2018~2021年GDP进行预测，预测结果分别为99213.01、107719.73、117995.68和128271.62。预测效果如图4所示，可以看出ARIMA(0,2,(2,3))去除常数项后模型对广东省GDP测试集数据的拟合效果是不错的。

Table 3. Test results of residual white noise

表3. 残差白噪声检验结果

Figure 4. GDP ARIMA model prediction effect in Guangdong Province from 2018 to 2021

图4. 广东省2018-2021年GDPARIMA模型预测效果

下面对广东省2018~2021年GDP的预测值和真实值进行比较分析，如表4所示。

Table 4. Analysis of ARIMA Model Prediction Results

表4. ARIMA模型预测结果分析

由表4可知，ARIMA拟合模型对广东省2018~2021年GDP预测的平均相对误差为0.029259552，近似2.93%。相对误差都在0.07以下，可以说明预测结果是好的，预测是有效的。2020年预测相对误差较大，我们考虑到是受到了新冠肺炎疫情的影响。

2.2. 基于指数平滑模型的广东省GDP预测

广东省1978~2017年GDP序列蕴含显著的线性递增趋势，对于含有线性趋势的序列，我们可以采用Holt两参数指数平滑进行预测。当时间序列数据是上升(或下降)的发展趋势类型，应在0.6~1之间取较大的平滑系数值 [4] ，故我们选取平滑系数 $\alpha =0.8$ ， $\beta =0.8$ 。

通过Holt两参数指数平滑法，不断迭代，得到最后一期的参数估计值为： $a\left(t\right)=88975.1$ ， $b\left(t\right)=9036.61$ 。

因此未来任意k期的预测值为： ${\hat{x}}_{t+k}=88975.1+9036.61k,\forall k\ge 1$ 。

基于Holt两参数指数平滑预测模型，对广东省2018~2021年GDP的预测结果分别为98011.71、107048.32、116084.93、125121.54，预测效果如图5。

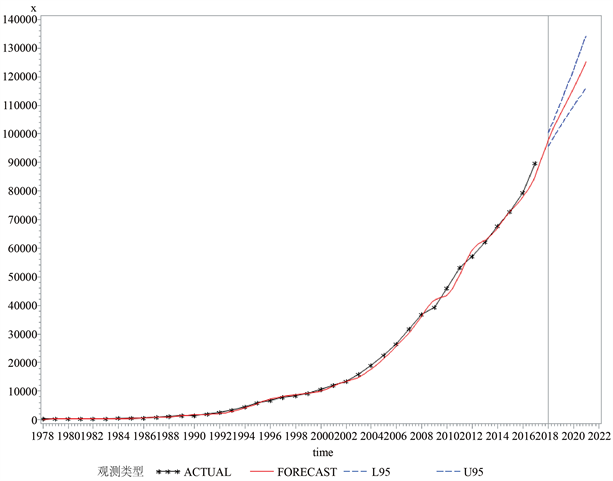
Figure 5. Prediction effect of the smooth model for GDP index in Guangdong Province from 2018 to 2021

图5. 广东省2018~2021年GDP指数平滑模型预测效果

下面对广东省2018~2021年GDP的真实值和预测值进行比较分析，预测结果分析如表5所示。

由表5可知，指数平滑预测模型对广东省2018~2021年GDP预测的平均相对误差为0.0168603615，近似1.69%。相对误差都在0.05以下，可以说明预测结果是好的，预测是有效的。2020年预测相对误差较大，我们考虑到是受到了新冠肺炎疫情的影响。

Table 5. Analysis of forecast results of exponential smoothing model

表5. 指数平滑模型预测结果分析

2.3. 基于组合预测模型的广东省GDP预测

对于权系数的确定，本文选取方差倒数法来讨论组合预测模型的预测结果。设在组合预测模型中共有k个单项预测模型(其中 $k=1,2,3,\cdots$ )， $w_i$ 是第i个单项模型在组合预测模型中的权系数，其中 $1\le i\le k$ ， ${\displaystyle {\sum }_{i=1}^k{w}_i}=1$ ，且 $w_i\ge 0$ 。

$w_i=\frac{D_i^{-1}}{{\displaystyle {\sum }_{i=1}^k{D}_i^{-1}}},i=1,2,\cdots ,k$

其中， $D_i$ 是第i个单项模型真实值与预测值之间差值的平方和， $D_i={\displaystyle {\sum }_{t=1}^n{\left(y_t-{\hat{y}}_t\left(j\right)\right)}^2}$ 。因此ARIMA模型预测结果的 $D_1=71314198.32$ ，Holt两参数指数平滑模型预测结果的 $D_2=29836663.50$ 。

通过上述分析，我们可以得到 $w_1=0.295$ ， $w_2=0.705$ ，构建方差倒数法组合预测模型： $f=0.295f_1+0.705f_2$ 。

基于方差倒数法组合预测模型，对广东省2018~2021年GDP的预测结果分别为98366.09、107246.39、116648.60和126050.81。

2.4. 预测模型的综合分析

我们结合平均绝对百分误差(MAPE)、残差平方和(SSE)、均方根误差(RMSE)和希尔不等系数(TheilC)对三种模型的预测结果进行综合分析，如表6所示。

Table 6. Comprehensive analysis of prediction models

表6. 预测模型综合分析

由表6可知，从MAPE和Theil IC来看，各模型的MAPE均小于3，Theil IC都小于1，说明各模型预测精准度高，预测效果好。其中Holt两参数指数平滑预测模型的MAPE值和Theil IC最小，预测精准度最高，而ARIMA预测模型的MAPE值和Theil IC最大，预测精准度在三种模型中最低。组合预测模型的MAPE、Theil IC均比ARIMA预测模型的小，比Holt两参数指数平滑预测模型的大，说明组合预测模型的预测精准度相对于ARIMA模型有所提高，相对于Holt两参数指数平滑预测模型准确度降低。

从SSE和RMSE来看，Holt两参数指数平滑预测模型最小，预测效果最好，而ARIMA预测模型的SSE和RMSE最大，预测效果在三种模型中最差。组合预测模型的SSE、RMSE均比ARIMA预测模型的小，比Holt两参数指数平滑预测模型的大，说明组合预测模型的预测效果相对于ARIMA模型有所提高，相对于Holt两参数指数平滑预测模型降低。

综合来看，对于广东省GDP数据的预测，预测效果最好的是Holt两参数指数平滑预测模型，其次方差倒数法组合预测模型，最后是ARIMA模型。由对比结果可以看出，在一定条件下，组合模型会优于部分单项模型，但当其中一项单项模型的准确度最高时，使用组合预测模型会降低预测效果。

3. 总结

本文先使用ARIMA模型进行拟合，确定ARIMA(0,2,(2,3))去除常数项后模型为拟合模型，模型通过了白噪声检验说明模型显著成立，利用该模型进行预测。接着，使用Holt两参数指数平滑模型对广东省GDP进行预测，确定两次平滑系数后，通过不断迭代得到最后一期的参数估计值，并得到未来任意k期的预测公式。最后，我们在这两种单项模型的基础上，建立了方差倒数法组合预测模型。

我们从MAPE、Theil IC、SSE和RMSE可以看出，三种模型预测精准度高，预测效果好。经过对比分析这三种预测模型，从短期的预测结果来看，预测效果最好的是Holt两参数指数平滑预测模型，其次方差倒数法组合预测模型，最后是ARIMA模型。从以上分析可以看出，在一定条件下，组合模型会优于部分单项模型，在一定程度上弥补单项预测模型的不足，但当其中一项单项模型的准确度最高时，使用组合预测模型会降低预测效果。

我们选取广东省1978~2021年GDP共44个数据作为本文实证分析的依据，由于数据样本相对较少，因此会对预测的精度有一定的影响。在之后的研究中，我们可以考虑将年度GDP数据扩展为季度GDP数据进行研究。

我们在拟合模型时，忽略了一些因素的影响。在实际问题的研究中，只把广东省GDP数据为预测的指标来考虑问题不是十分全面，如我们没有考虑到国家政策、自然灾害或者重大传染性疾病等其它因素带来的影响。2020年的新冠肺炎疫情爆发对广东省GDP的增速产生了影响。在之后的研究中，我们可以考虑把自然灾害等影响经济的因素加入到模型中进一步完善模型。