1. 引言
金融市场在现代经济系统中的中介地位举足轻重。货币在短期是非中性的,中央银行通过调节货币的供给影响市场利率、资产价格和实体经济。准确、高效地使用货币政策工具调节金融市场维稳实体经济、提升经济发展质量对我国达成构建现代化产业体系目标,并最终实现中国式现代化建设目标具有重要推动作用。在这种背景下我们不禁产生疑问:如何提升中央银行偏好刻画的准确性?货币政策是否盯住资产价格波动?如果是,其调控的模式是怎样的?然而,现有的研究还不能充分解答这些问题。
与货币政策和资产价格波动相关的研究主要从中央银行的偏好行为、货币政策规则的形式、资产价格的纳入方式以及模型的估计方法等方面展开。但已有文献忽视了“中央银行对资产价格波动风险的非对称和‘区域’损失偏好假设”。这可能导致对包含资产价格波动风险的货币政策规则的估计结果产生偏差。因此,本文尝试将“灵活”偏好损失函数引入中央银行对资产价格波动风险的调控模型。本文的边际贡献主要有以下三点:1) 构建针对资产价格波动的指数——幂函数损失偏好函数,以反映中央银行的偏好行为特征;2) 通过构建动态经济系统从理论层面考察中央银行非对称、“区域”偏好行为对最优货币政策调控模式的影响;3) 构建GDP实时数据集,利用实时宏观经济数据和股票市场数据对本文拓展的货币政策调控模型进行实证检验。
2. 文献综述
作为金融系统和实体经济的主要联通渠道,货币政策传导机制一直是学术界关注的焦点。通过梳理文献发现,与本文相关的文献主要包含三个方面:中央银行偏好研究、货币政策是否应对资产价格作出反应相关研究以及中央银行怎样对资产价格作出反应研究。
中央银行的偏好行为是货币政策调控模式的重要决定因素。早期的研究多基于“中央银行的偏好具有对称性”这一假定,围绕利率和货币供应量这两个操作目标展开,比如麦卡勒姆规则 [1] 和泰勒规则 [2] 这两个著名的货币政策规则。然而,后来的研究证实了“中央银行实际上具有非对称性偏好”。Surico [3] 发现相比于通货膨胀,美联储更加厌恶通货紧缩。Caglayan等 [4] 使用GMM方法证实了加拿大和英国的货币政策制定者对国内通胀和产出缺口作出的反应非对称。此外,一些学者发现单纯地使用非对称函数并不能完全刻画中央银行的偏好行为,提出用“区域”偏好损失函数刻画中央银行的偏好行为。例如,Boinet和Martin [5] 发现英国中央银行只有通胀偏离目标通胀一定的距离才会积极地采取行动;刘晓星和张旭 [6] 提出一种新型的损失函数来刻画中央银行的偏好行为,证实了中央银行对实时产出缺口具有“区域”偏好,而对通货膨胀则没有。此外,张旭和刘晓星 [7] 利用混频数据模型实证发现中央银行的偏好行为具有“区域”特征。
中央银行的货币政策是否应该对资产价格波动作出反应是货币政策规则研究的重点内容。支持货币政策对资产价格波动作出反应的学者认为,资产价格(股票流动性、经济指标、住房市场变动等)是宏观经济的重要影响变量,对实体经济具有预期作用 [8] [9] 。而持反对意见的学者则认为中央银行对资产价格波动作出反应的后果具有滞后性和不确定性。除非货币政策对资产价格变化的反应有助于预测通胀和通缩,否则央行没有必要作出反应,而且资产价格信息不仅由经济基本面决定,还受其他非基本面信息的影响,清晰的区分这两者十分困难,因此不应当对资产价格波动作出反应 [10] 。
目前关于货币政策应该考虑哪些资产价格的变动,如何对其做出反应目前尚未达成共识。一些学者提出将股价、汇率等具体的资产价格纳入货币政策反应函数。Hollander和Liu [11] 采用贝叶斯模型证实一个带有股票价格的DSGE模型能够很好的模拟美国经济周期,并强调金融市场不稳定将沉重打击实体经济。王学龙和石振宇 [12] 在新凯恩斯三方程框架基础上加入金融周期方程和汇率决定方程,发现将汇率波动和金融不稳定纳入考虑的货币政策能够削弱汇率和金融波动对产出缺口和通胀的冲击,证实了货币政策应该对汇率波动和金融不稳定做出明确积极的反应。Galí [13] 构建一个新凯恩斯主义拓展模型,并提出了能够有效抑制资产价格泡沫的新的货币政策规则类型。
已有文献忽视了中央银行对资产价格波动风险的非对称和“区域”损失偏好行为,这会影响估计包含资产价格波动风险的货币政策规则准确性。因此,本文考虑将“灵活”偏好损失函数引入中央银行对资产价格波动风险的调控模型,通过推导得到包含资产价格波动的最优货币政策反应函数模型。
3. 考虑“区域”——非对称偏好的拓展型货币规则
鉴于货币当局在资产价格大幅波动时采取逆向操作事实,本文在刘晓星和张旭 [6] 、Boinet和Martin [5] 等研究的基础上将资产价格波动引入最优货币规则模型,通过货币当局的“区域”——非对称偏好行为反映货币当局对资产价格波动的“相机抉择”调控模式。
3.1. 中央银行偏好函数
中央银行的损失偏好函数刻画了其政策盯住目标变化对其损失厌恶的影响程度。在“区域”——非对称偏好假设条件下,中央银行对其盯住目标轻微变化并不做出反应或者做出极小程度的反应,因此,可以用来刻画中央银行对资产价格波动风险的反应模式。鉴于此,我们在刘晓星和张旭 [6] 研究的基础上,将资产价格波动风险引入货币政策的损失偏好函数,构建如下形式的中央银行损失偏好函数:
(1)
其中,
表示中央银行的偏好损失,
表示中央银行利率水平,
为通货膨胀率,
为通货膨胀目标,
为通货膨胀缺口,
为产出缺口,
表示资产价格缺口。
、
、
分别表示中央银行损失偏好对通货膨胀缺口、产出缺口和资产价格缺口的敏感系数,
表示长期利率。参数
表示中央银行对资产价格波动风险的非对称偏好程度,
意味着中央银行对资产价格下跌风险所赋予的权重大于上涨所赋予的权重,这意味着中央银行更加厌恶资产价格下跌,而
意味着中央银行更加厌恶资产价格上涨(如图1所示)。

Figure 1. Asymmetric morphological characteristics of loss function
图1. 损失函数的非对称形态特征
式(1)中,参数
表示中央银行对资产价格波动的“区域”反应程度。
时,式(1)表示中央银行具有“区域”偏好。如图2所示,在“区域”偏好下,资产价格大幅波动风险对中央银行的损失影响更大,
的大小反映了这种“区域”偏好的强度,比值越大,中央银行越重视资产价格大幅波动。而当
时,式(1)则表示小幅波动对中央银行损失偏好的影响越大,其更加重视资产价格小幅波动风险,因此,可以通过调整
、
的相对大小构造多种形态的央行偏好行为。
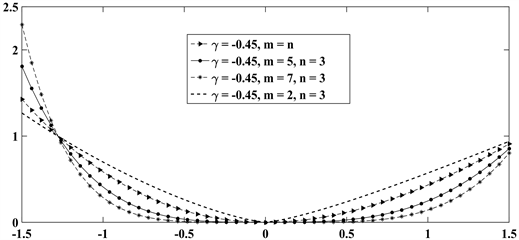
Figure 2. The “region” morphological characteristics of the loss function
图2. 损失函数的“区域”形态特征
3.2. 动态经济系统
为了推导最优的货币政策规则形式,首先需要构建一个动态经济系统。本文参照陆前进、李成等 [14] [15] 等人的方法,构建如下兼具前瞻性和后顾性形式的动态经济系统:
(2)
(3)
(4)
其中,
,
,
,
,
,
和
分别为经济系统的总需求冲击和总供给冲击,
表示资产价格波动冲击。参数
、
、
的大小决定了方程的类型,例如,
意味着后顾性总供给曲线,而
意味着前瞻性总需求曲线。对式(2)、(3)和(4)简化,得到:
,
,
。其中,
,
,
。
3.3. 最优货币政策调控规则
根据传统的货币理论,中央银行通过最小化其福利损失函数来达到控制其调控变量的目的,可以表示为:
(5)
其中,
表示央行损失函数的贴现率。因此,式(1)、(2)、(3)、(4)和(5)构成了基本的货币政策调控模式。中央银行通过调节每一期的利率水平最小化其福利损失,对模型进行求解,得到一阶最优条件:
(6)
其中,
,
,
。
进一步对模型(6)线性化处理,即在
处进行泰勒展开,得到:
(7)
其中,
,
,
,
。
本文进一步参照货币政策反应函数的通常做法,在最优货币政策规则方程(7)的基础上引入利率平滑参数
,得到:
(8)
其中,
,
,
,
,
,
。
表示扰动项,
表示货币政策操作利率,
表示根据货币规则得到的理论利率水平。式(8)即为考虑资产价格波动风险的货币政策反应函数,通过调节
的大小,可以实证检验中央银行对资产价格波动反应的“区域”偏好特征和非对称特征。
4. 估计方法与数据说明
4.1. 模型估计方法
在“灵活”偏好条件下,中央银行对资产价格波动风险偏好呈现出非对称和“区域”特征。然而,直接对存在内生性问题的模型(8)估计比较困难,因此,本文参考刘晓星和张旭 [6] 的做法,对模型(8)展开,得到如下形式:
(9)
其中,
,
,
,
,
,
。
模型(9)即为本文用于实证分析的模型。从本文推导的“灵活”偏好的最优货币规则模型(8)可以看出,扰动项
中包含通货膨胀缺口、产出缺口和资产价格波动缺口的预期偏差,这些预期偏差显然与模型中的通货膨胀缺口、产出缺口和资产价格缺口变量存在相关性,因此,模型设定中假设了存在内生性问题,为此需要采用合理的工具变量进行模型修正,得到一致性参数估计结果。
虽然,一些新的估计方法,例如,区制转换回归、分位数回归、混频回归等参数估计方法可以考察不同状态或条件下的参数差异问题,但是其往往不能很好地解决内生性问题,为此,本文参照以往广泛使用的广义矩估计方法进行参数估计。具体来说,广义矩估计方法通过最小化如下形式的残差平方和
得到参数估计结果:
(10)
其中,
为参数向量,Z为工具变量,X为被解释变量,X为解释变量,W表示权矩阵。根据最优化模型(10)的一阶条件,得到模型参数的广义矩估计结果:
(11)
4.2. 变量与数据说明
4.2.1. 资产价格波动指标
在本文的研究中,我们使用股票价格作为资产价格的代理指标。为此,本文根据式(9),分别测度“灵活”偏好参数下的股票价格波动指标
和
。本文选取上证综合指数作为基础变量,选取的时间范围为1992年1季度至2022年2季度。对于股价指数的处理,本文首先取自然对数,然后使用H-P滤波方法测度股票价格波动的周期项,进一步选取“灵活”偏好参数
和
,测度不同参数组合下的股票价格波动风险指标。图3给出了本文测度的股价风险指标例子,其中,
,
。从图中可以看到,
与股价波动缺口数据Q保持一致的符号和变动趋势,同时发现,在Q数值接近0时,两者的差距并不大,但是,在
风险较大时,两者的差距开始显现,并且,
显著小于Q,这意味着在其他条件不变的前提下,中央银行对
的反应系数会显著大于对Q的反应系数,这恰好反映了中央银行的“区域”偏好特征。
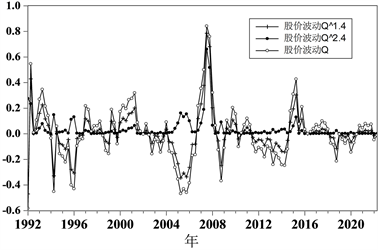
Figure 3. Index of stock price volatility risk
图3. 股价波动风险指标
4.2.2. 实时产出缺口
近年来,宏观经济学研究更加注重宏观经济信息的提取质量。准确地提取宏观经济变量对于宏观经济走势的把握和调控具有更加重要的意义。鉴于实时GDP数据在货币政策研究中的重要作用 [6] ,本文考虑构建实时GDP数据集,在此基础上提取实时GDP缺口数据。本文参照刘晓星和张旭 [7] 的实时GDP数据集构建策略。
图4显示了本文采用H-P滤波方法估计的实时GDP缺口和最终GDP缺口。从图中可以看出,实时GDP缺口和最终GDP缺口序列在整体上保持了一致的变化趋势,特别是最近10年,两者逐渐趋同,说明统计局实时公布的GDP初步核算数据越来越准确。而在样本期初,两者的统计差距较大。在2002至2006期间,实时GDP数据和最终GDP数据也呈现出较大差距,因而,使用最终GDP数据进行货币政策研究可能会导致较大的估计误差。

Figure 4. Real time GDP gap and final GDP gap
图4. 实时GDP缺口和最终GDP缺口
4.2.3. 名义利率
在货币政策规则相关的研究中,往往使用全国银行间同业拆借市场7天期限的同业拆借利率作为货币政策的操作变量 [6] [16] [17] 。由于中国人民银行网站只公布1996以来的同业拆借利率数据1,对于1992年至1995年的利率数据,本文参照通常的做法,使用谢平和罗雄 [16] 提供的上海融资中心的融资利率补齐。图5显示了货币政策工具7天期同业拆借利率的变化趋势。可以看到,我们国家的利率水平在2000年之后保持了较为稳定的变动趋势,而在2000年以前,为了抑制通货膨胀,采取了较为激进的紧缩型货币政策,导致了较高的利率水平。
4.2.4. 通货膨胀缺口
本文根据国务院每年公布的《关于××××年国民经济和社会发展计划执行情况与下一年年国民经济和社会发展计划草案的报告》中设定的通货膨胀目标,测算通货膨胀缺口数据。图5给出了通货膨胀缺口的测算结果。可以看出,在剔除掉通货膨胀目标之后,通货膨胀缺口数据仍然呈现出周期波动的趋势,因此,需要货币政策工具进行逆周期调节。在1996年以前,我国的通货膨胀率保持在了较高的位置,但之后在紧缩性货币政策调控下逐渐趋于稳定并保持在较低的水平。
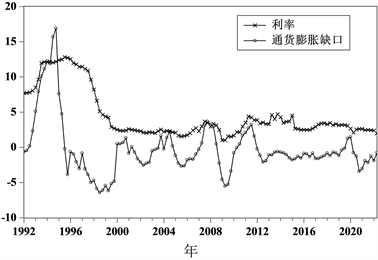
Figure 5. Nominal interest rates and inflation rates
图5. 名义利率和通货膨胀率
5. 实证分析
5.1. 非对称偏好检验
为验证选择使用非对称偏好假设的合理性,本文使用参数约束检验方法进行偏好非对称检验。由于无法对进行约束检验,本文参考张旭和刘晓星 [7] 的做法进行间接检验,具体来说,我们对反映非线性成分的参数,即模型(9)中
施加约束,假设其等于0,然后使用Wald检验方法进行约束检验。为了获得稳健的结果,我们分别设置6种灵活偏好模型,包括模型1 (
、
)、模型2 (
、
)、模型3 (
、
)、模型4 (
、
)、模型5 (
、
)和模型6 (
、
)。Wald检验的结果如表1所示。从表中可以看出,t统计量和
统计量均在5%显著性水平下拒绝原假设,说明模型参数
并不显著为0,拒绝央行对资产价格波动风险呈现对称偏好的假设,这意味着本文使用非对称偏好形式进行货币政策调控研究是合理的。

Table 1. Central bank asymmetric preference test results
表1. 央行非对称偏好检验结果
注:*、**、***分别表示在10%、5%和1%的水平上拒绝原假设。
5.2. 模型参数估计结果
借鉴刘晓星和张旭 [6] 工具变量设置方法,本文选取解释变量的滞后1至8期作为广义矩估计的工具变量。本文根据灵活偏好的设定参数,分别选取6个模型进行参数估计。模型的估计结果如表2所示。从表中可以看出,大部分的参数估计结果通过了5%的显著性检验。J统计量的P值显著大于5%,说明本文选取的工具变量是适当的。从参数估计值来看,货币政策的利率平滑参数
均大于0.98且小于1,这符合我们的理论预期,说明我国中央银行的货币政策操作具有较强的连续性和平滑性。从通货膨胀缺口的参数
估计结果来看,均通过了1%显著性检验,为了对比,本文还估计不包含资产价格波动风险的货币政策反应函数,可以看出,其通货膨胀缺口的系数并不显著。而考虑资产价格波动风险后,通货膨胀缺口的估计系数通过显著性检验,并且系数增大。对于产出缺口的系数
,只有模型1 (
、
)的估计结果在5%的水平下显著,而其他模型的估计结果均不显著,但其系数为正,符合我们的理论预期。这与张旭和刘晓星 [7] 、郑挺国和王霞 [18] 、Zhang等 [19] 的结论是一致,说明中央银行的盯住目标主要是通货膨胀,这与其官方的货币政策目标声明是一致的。

Table 2. The estimated results of the model parameters
表2. 模型参数估计结果
注:S.E.表示模型估计的标准差,SSE为模型估计的残差平方和。*、**、***分别表示在10%、5%和1%的水平上拒绝原假设。
进一步分析股票价格波动风险系数的估计结果。从表2可以看出,对于
项的系数
估计结果,除模型1 (
、
)通过10%的显著性水平,其他变量均在1%的显著性水平上显著,并且估计结果为正,说明中央银行对资产价格波动风险具有逆周期的调节模式。对于
项的系数
估计结果,均在1%的显著性水平上显著,并且参数估计结果显著为负,说明中央银行的偏好具有显著的非对称性,这表明中央银行更加厌恶资产价格下跌风险,而对资产价格上涨的风险的重视程度相对较低。
总体来看,我国中央银行对资产价格波动风险具有显著的逆周期调节模式,其对资产价格波动风险的偏好具有显著的非对称性和“区域”偏好特征,相比资产价格上升带来的损失偏好,中央银行更加厌恶资产价格下跌带来的损失偏好,灵活偏好的货币政策反应函数更适合中国货币政策调控的基本情况。
5.3. 中央银行“灵活”偏好重构
为了进一步验证中央银行的损失偏好形态特征,本文根据模型的参数估计结果和实证数据对中央银行关于资产价格波动风险的损失偏好进行重构。具体来说,根据式(9),可以计算中央银行对资产价格波动风险的非对称偏好参数
,计算结果如表3所示。

Table 3. Calculation results of asymmetric preference parameters of central bank to asset price volatility risk
表3. 央行对资产价格波动风险的非对称偏好参数计算结果
从表3可以看出,中央银行对资产价格波动风险的损失偏好具有显著的非对称性,并且非对称参数为负,说明相比于资产价格上升风险,中央银行更加厌恶资产价格下跌风险。进一步根据损失偏好函数(式(1)),作图得到中央银行对资产价格波动风险的损失偏好函数图,结果如图6所示。可以看出,中央银行对资产价格波动风险的偏好函数具有显著的非对称性。此外,我们还发现,中央银行对资产价格波动风险的偏好特征具有显著的“区域”特征或“惰性”特征,即中央银行对资产价格小幅波动并不在意,其主要针对资产价格大幅波动作出反应。并且,这种“区域”反应程度随着“灵活”偏好参数的变化而变化。这些结论意味着具有非对称——“区域”偏好特征的资产价格波动风险反应函数更适合中国的宏观经济调控的基本情况。
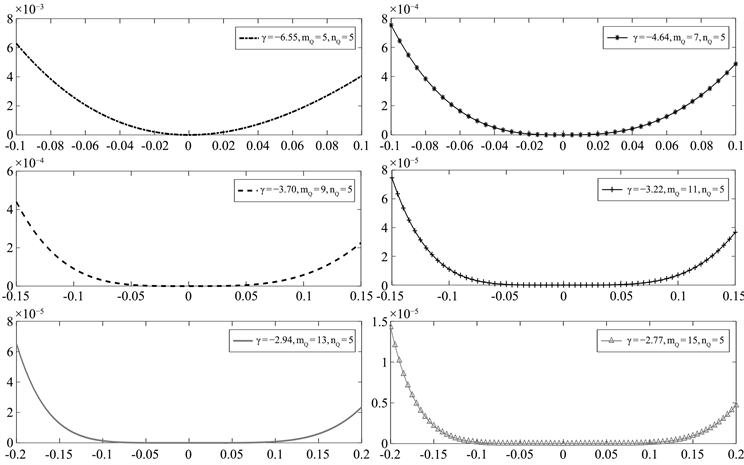
Figure 6. Restructure the flexible preference of Central bank
图6. 央行灵活偏好重构
5.4. 稳健性检验
本文从灵活偏好的视角研究了我国中央银行对资产价格波动风险的调控模式。为了验证研究结论的稳健性,本文从以下三个方面进行稳健性检验:
第一,使用不同的“区域”偏好参数进行稳健性分析。本文分别选取6种基于灵活偏好参数的模型进行实证研究,结果如表2所示。可以看出,中央银行在6种偏好假设下均具有显著的“区域”偏好特征,并且,6个模型参数估计的显著性、系数大小和符号均较为一致。
第二,替换解释变量。为检验不同的通货膨胀缺口是否对结果造成影响,本文进一步借鉴郑挺国和王霞 [18] 的方法,将通货膨胀目标统一设定为4%,重新估计模型结果。替换变量的估计结果如表4所示。可以看到,模型估计参数的显著性、符号和大小均未发生显著变化,说明本文的估计结果较为稳健。

Table 4. Robustness test (replace inflation gap data)
表4. 稳健性检验(替换通货膨胀缺口数据)
注:S.E.表示模型估计的标准差,SSE为模型估计的残差平方和。*、**、***分别表示在10%、5%和1%的水平上拒绝原假设。
第三,替换工具变量。由于本文设定的模型自身存在内生性问题,为此,需要进一步检验模型的工具变量变化是否会对主要结论产生影响。本文替换原来的工具变量,选取解释变量的滞后1至6阶变量作为工具变量,重新对模型进行估计,估计结果如表5所示。可以看到,除产出缺口估计系数不显著外,其他参数的估计值的显著性、符号和大小均未发生显著变化。综合来看,本文的实证结论是稳健的。

Table 5. Robustness check (replace tool variables)
表5. 稳健性检验(替换工具变量)
注:S.E.表示模型估计的标准差,SSE为模型估计的残差平方和。*、**、***分别表示在10%、5%和1%的水平上拒绝原假设。
6. 结论性评述
本文的研究发现,我国中央银行的重要盯住指标是资产价格波动风险,中央银行对资产价格波动风险的调控呈现出显著的逆周期模式,并且,中央银行对资产价格波动风险的损失偏好函数具有显著的非对称性,即相比资产价格上升带来的损失偏好,中央银行更加厌恶资产价格下跌带来的损失偏好。此外,中央银行的损失偏好还呈现出“区域”特征,即中央银行对资产价格小幅波动并不在意,其主要针对资产价格大幅波动作出反应。这些结论意味着我国中央银行主要通过“区域”——非对称偏好行为对资产价格波动风险作出反应。
本文的研究框架、内容和结论对理解我国货币政策调控模式、提升资产价格波动风险的管理效果具有重要的价值:第一,在对货币政策规则进行理论与实证研究时,应该将资产价格波动因素纳入研究框架,考虑基于频域的视角深入挖掘数据信息,构建更加完善的资产价格与货币政策监控模式,以及能够反应重要资产及价格的集成指数,以便随时观测市场动态,及时进行政策调整。第二,在货币政策的研究中不能忽视央行偏好行为对其调控模式的影响,央行应该清晰地掌握自己的偏好特征,基于中国实际情况完善已有的货币政策损失函数,使其达到更好的拟合效果,为日后货币政策调控提供参考。第三,本文仅考察了中央银行对股票市场波动风险的反应,这样所得到的结论对资产价格与货币政策的关系的反应可能会损失一些信息,在后续的研究中可以考虑将房地产市场、外汇市场、债券市场引入,也可以考察中央银行对金融状况指数的调控模式,通过将“灵活”偏好函数引入动态经济系统来考察货币政策对宏观经济盯住变量的作用机理和实施效果。
基金项目
江苏省社会科学基金青年项目“‘双支柱’框架下基于机器学习的货币政策调控模式创新研究”(20EYC011);教育部人文社会科学研究青年基金项目“中国股票市场重大风险的生成机理、甄别与治理研究——基于市场流动性供需失衡视角”(18YJC790226);国家自然科学基金“金融市场异常波动的共振效应及其智能监控研究”(71903097);江苏省基础研究计划(自然科学基金)“金融资产价格极端波动的共振机理及其风险防范研究”(BK20190767);中国博士后科学基金特别资助“基于流动性供需失衡的中国股票市场‘高波动之谜’研究”(2021T140335);中国博士后科学基金面上资助“宏观经济动量研究”(2021M691635)。
NOTES
1按照通常的做法,本文对7天期限的月度同业拆借利率进行加权平均得到季度名义利率,计算公式为:
,其中,
为季度名义利率,
、
为当季第j月份的利率水平和交易量。