1. 引言
人们经过对混凝土搅拌设备几十年的研究,从滚筒自落式搅拌、卧轴强制式搅拌的基础上,提出了振动搅拌理论,并发展出了立轴振动搅拌、双卧轴振动搅拌等新型搅拌设备 [1] [2] [3] 。对于高频振动搅拌设备而言,激振器所产生的振动频率对搅拌质量的影响非常大 [4] [5] 。振动频率过低将达不到分散水泥颗粒,加速水化反应的效果。较高的振动频率可以破坏水泥浆体的团聚作用,把水泥颗粒充分打散,加速水泥浆的水化反应过程。而振动频率过高也会使混凝土组份中的细集料和粗骨料快速分离,导致离析的出现。传统的试验研究方法耗时较长,使用EDEM离散元仿真的方法已广泛应用于建筑、化工、制药等相关领域 [6] [7] [8] [9] 。本文通过EDEM软件,设置了0 Hz、25 Hz、50 Hz、75 Hz和100 Hz五种不同的频率,分析了在这五种激振频率下,搅拌过程中和搅拌完成后的各组份分散情况。
2. 搅拌设备的情况

Figure 1. 3D model diagram of mixing mechanism
图1. 搅拌机构的三维模型
创建搅拌机的三维模型,其搅拌筒为内径405 mm,高度460 mm,壁厚5 mm的圆筒。搅拌机构由法兰盘,搅拌臂,搅拌叶片组成,三者通过螺栓连接,如图1所示。搅拌臂通过其上方的法兰盘与旋转轴相连。搅拌过程中搅拌臂绕搅拌筒中心旋转,激振器位于搅拌筒中心,相对搅拌筒静止,不进行旋转运动,只以圆锥摆动的形式进行振动。振动能量的分布及传播如图2所示。
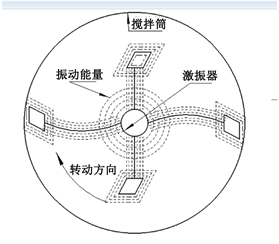
Figure 2. Schematic diagram of vibration energy distribution and propagation
图2. 振动能量分布和传播示意图
3. 搅拌过程的离散元仿真
3.1. 颗粒设置
EDEM离散单元法是在仿真过程中将每一个颗粒视作一个单元,在颗粒与颗粒之间,颗粒与边界之间添加接触模型,根据接触模型计算相关接触参数。再根据牛顿第二定律来计算颗粒的运动轨迹。
离散元仿真软件EDEM有多种颗粒模型,常用的主要有球形模型和球叠模型两种,如图3所示。
球叠模型更接近真实情况,球形模型的仿真算法更容易实现,在计算精度变化不大的情况下,计算时间更少 [10] 。为了降低仿真的计算量,提高仿真的效率,本文采用的仿真颗粒模型均采用单一软球形颗粒模型。
由于所用计算机性能有限,因而此次仿真过程只添加大石子、小石子、砂子、水泥四种颗粒,根据材料属性的不同可将其分为骨料颗粒和水泥颗粒两种。标准差设置为0.05,材料设置为连续集配。通过改变模型的接触参数来模拟水和外加剂对搅拌过程的影响。此次仿真的搅拌样机材料为钢。颗粒参数设置如表1所示,材料属性设置如表2所示。
搅拌样机公称容积30 L,各颗粒投放质量按照C30配合比设计,颗粒投放按照固定质量法,各颗粒投放质量见表3所示。

Table 3. Mass of particle placement
表3. 颗粒投放质量
3.2. 接触设置
搅拌机在对材料进行搅拌时,不同颗粒之间、颗粒与搅拌样机之间会产生多种接触。对每个接触对进行设置,接触参数如表4所示。
颗粒是否含水及含水量的大小对搅拌效果有很大的影响,这主要在接触模型中体现 [11] [12] 。水泥混凝土作为一种宾汉姆材料,其组成成分和所产生的接触作用与Hertz-Mindlin with JKR接触模型最为相似。因此,选用Hertz-Mindlin with JKR模型添加到颗粒与颗粒间的接触。选择Hertz-Mindlin (no slip)模型。添加到颗粒与搅拌装置和搅拌筒等的接触。
3.3. 机器参数设置与仿真参数设置
综合考虑计算机的运算速度和搅拌机的搅拌效果,混凝土搅拌机搅拌线速度宜选择在1.4~1.7 m/s [13] [14] ,该搅拌装置实际正常工作的搅拌转速为72 r/min,换算后线速度为1.52 m/s,满足要求。因此设置搅拌装置转速为72 r/min。时间步长设置为Rayleigh Time步长的5%~40%之间时,能够保证仿真的稳定进行,因此,本次选取时间步长为35% Rayleigh Time,而网格划分设置为仿真模拟颗粒的最小尺寸半径的2倍 [15] 。
本文主要分析激振器在不同振动频率下对搅拌效果的影响。因此,在模拟仿真中仅改变激振器频率这一个参数。分别设定为0 Hz (无振动)、25 Hz、50 Hz、75 Hz和100 Hz这五种参数。仿真过程中,激振器的振幅设置为0.8 mm,除了频率发生改变之外,其余参数均不变。
3.4. 进行仿真
仿真总时长为32 s,其中总投料时间5 s,总搅拌时间25 s,卸料过程2 s。在第5 s时,仿真颗粒投料完成,如图4(a)所示。第5 s开始,搅拌转轴开始搅拌,高频激振器振幅0.8 mm,以0 Hz振动频率为例,搅拌时间7.5 s、15 s、22.5 s和30 s的搅拌过程如图4(b)、图4(c)、图4(d)和图4(e)所示。
卸料工序同样对混凝土的质量产生影响,卸料过程如图4(f)所示。
由图4(a)所示,本次仿真选择分层撒布的投料方式,物料投放层次分明,其中红色为大石子颗粒,橙色为小石子颗粒,蓝色为砂子颗粒,青色为水泥颗粒。投料5 s后,搅拌装置开始搅拌,在7.5 s时,各物料颗粒迅速被打散,底层的红色颗粒被提升到拌筒上层,而最上层的青色水泥颗粒迅速下移,但是同种颗粒堆积现象依然比较严重。如图4(c)所示,在搅拌时间15 s时,颗粒在搅拌装置强力剪切的作用下,水泥颗粒不断混合,但其他颗粒却未能很好的被搅拌均匀,还存在颗粒堆积。图4(d)和图4(e)所示,随着搅拌时间的不断推移,颗粒不断混合均匀,在搅拌时间30 s时,无颗粒堆积现象,水泥颗粒将所有颗粒包裹完全,所有颗粒基本已经搅拌均匀,搅拌完成进入卸料过程,如图4(f)。
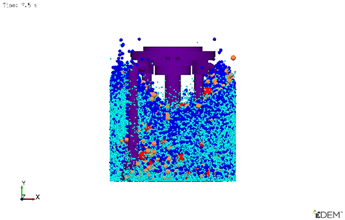

(a) 投料完成 (b) 搅拌7.5 s
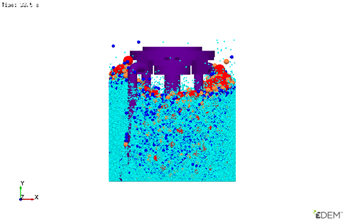
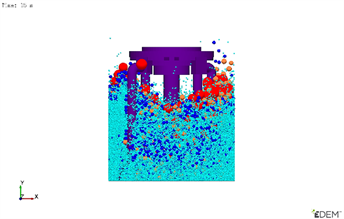 (c) 搅拌15 s (d) 搅拌22.5 s
(c) 搅拌15 s (d) 搅拌22.5 s
 (e) 搅拌30 s (f) 卸料过程
(e) 搅拌30 s (f) 卸料过程
Figure 4. Schematic diagram of the whole mixing process
图4. 整个搅拌过程示意图
4. 结果分析
仿真过程中,随着时间的推移,颗粒的分布状态从最初的离散分布逐渐达到理想的均匀分布状态。在离散元仿真软件EDEM后处理模中,对仿真模型进行网格划分。Guilkey [16] 建议在模拟大变形问题中采用较高的质点密度。Coetzee [17] 发现随着网格的细化,模拟仿真的精度不断提高。综合考虑计算效率和仿真精度,将仿真区域划分为10 × 12 × 10个立方体单元,如图5所示。
通过分析各个时刻的颗粒在各网格中的分布情况,可以确定混合均匀程度。为了保证结果的准确性,以颗粒总数为30作为临界值,剔除小于临界值的单元。
以某一粒径颗粒为例,设总网格数目为m,第i个网格内颗粒数目为ni,网格内颗粒总数目为Ni。
每个网格内该粒径颗粒占比:
(1)
在理论上所有颗粒混合均匀时,该粒径颗粒占所有颗粒的比值:
(2)
该粒径颗粒的离差:
(3)
对其进行均值和标准差计算:
(4)
(5)
则该粒径颗粒的离差系数为:
(6)
同理,可以按照上述公式计算其他粒径颗粒在不同时刻的搅拌混合均匀度离差系数。
定义四种颗粒搅拌混合后的离散程度大小为混合离散度,计算公式如下式(7),其中1代表水泥颗粒,2代表砂子颗粒,3代表小石子颗粒,4代表大石子颗粒。St表示在某种频率下,搅拌时间为t时,四种颗粒被搅拌混合后整体的混合离散度。
(7)
式中:
p——颗粒占比;
Cv——颗粒离差系数;
t——搅拌时间。
由上式(7)计算从搅拌时间第5 s开始,五组不同振动频率下的混合离散度,结果保留小数点后四位。混合离散度可以反映整个搅拌过程中所有颗粒的离散程度。混合离散度数值越大,颗粒的离散程度越大,搅拌后的均匀性越差。混合离散度越小,整体混合程度越高,搅拌均匀性越好,搅拌质量越好。混合离散度计算结果如表5所示。
为了更直观的反映所有颗粒的混合程度,直观反映搅拌效果随时间的变化关系,将所计算出的混合离散度的结果绘制如图6所示的点线图。
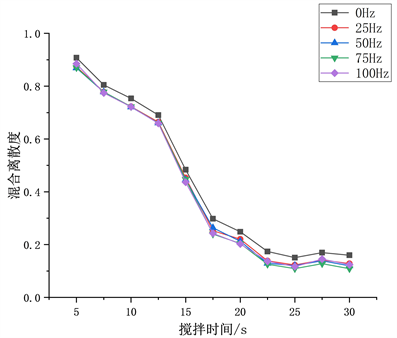
Figure 6. Mixed dispersion curve with time
图6. 混合离散度随时间变化曲线
由图6可得,随着时间的增大,混合离散度逐渐减小,四种颗粒混合均匀程度变得更好。在振动频率为0 Hz下,混合离散度较其他组大,颗粒混合尚未完全达到均匀状态。振动频率为75 Hz时,混合离散度最小,而振动频率增加到100 Hz时,混合离散度反而增大。
结果表明,随着振动频率的增大,颗粒间的扩散和碰撞运动加剧,混合料的均匀性增大。但是,振动频率过大会对搅拌过程产生负面影响。
5. 结语
1) 随着振动频率不断增大,搅拌物料的均匀性为先增大后降低的趋势,在振动频率75 Hz时,搅拌物料的均匀性最优,而振动频率继续增大则均匀性又呈现降低的趋势。
2) 振动频率过大对搅拌效果产生了负面影响。
3) 振动频率0 Hz (无振动搅拌组),与其他施加振动频率组(振动搅拌组)相比,搅拌的均匀性最差,表明振动搅拌对搅拌过程具有强化作用,能够提高被搅拌物料的均匀性。
基金项目
陕西省交通运输厅科技项目:水泥混凝土振动搅拌技术在铁路工程中的应用(编号:17-28K/211825180109)。
NOTES
*第一作者。
#通讯作者。