紧凑型光学涡旋发射装置设计

Compact Optical Vortex Launcher Design

摘要: 硅基集成平台由于其较高的折射率差，适合用于大规模、小尺寸、高密度器件的集成。本文提出了一种基于硅基光子学的光学涡旋发射装置，工作波长在1600~1800 nm范围，通过改变输入光的波长可以输出不同拓扑荷的涡旋光束。同时，通过在环形波导外侧壁刻蚀二阶布拉格光栅的方法，克服了固有的高折射率对比度带来的左旋圆偏振光和右旋圆偏振光的叠加问题，得到了高纯度的单一圆偏振标量涡旋光束。

Abstract: The silicon-based integration platform is suitable for the integration of large-scale, small-size, and high-density devices due to its higher refractive index difference. In this paper, an optical vortex emission device based on silicon-based photonics is proposed, operating in the wavelength range of 1600~1800 nm, and vortex beams with different topological charges can be output by changing the wavelength of the input light. Meanwhile, by etching a second-order Bragg grating on the outer sidewall of the ring waveguide, the superposition of left- and right-hand circularly polarized light brought by the inherent high refractive index contrast is overcome, and a single circularly polarized scalar vortex beam of high purity is obtained.

1. 引言

绝缘体上硅(Silicon-On-Insulator, SOI)是当前公认的具有很大潜力的光电子集成材料 [1] ，它允许将传感器、检测器、光源和读出电子器件集成在一个芯片中 [2] [3] [4] [5] [6] ，这为大规模生产提供了可扩展的平台 [7] [8] ，并为电子和光子器件的单片集成提供了机会，被称为电子光子集成电路(Electronic-Photonic Integrated Circuits, EPICs) [9] 。SOI主要由硅芯层、掩埋氧化物层(Buried Oxide, BOX)、硅衬底层构成，不同的集成光电子器件被制备在硅芯层中，被称为器件层。SOI由于硅芯层(n = 3.47)和包层(一般为氧化硅n = 1.45或者空气n = 1)之间的高折射率对比，它对1550 nm波段的通信波长上具有很强的光约束能力。目前，将光限制在亚微米范围内的低损耗硅波导已在CMOS兼容工艺中实现 [10] 。其它硅基光电子器件，如调制器和光电探测器也被证明具有高性能 [11] ，在高速通信方面有着广阔的应用前景。

光的轨道角动量(Orbital Angular Momentum, OAM)的发现改变了我们理解和使用光的方式。随着集成光子学的发展，基于绝缘体上硅(Silicon-on-Isolator, SOI)的片上可集成光学涡旋发射装置被不断报道出来。局限于平面波导中圆柱形矢量模式的一个特例是沿圆形结构(例如微盘和微环)圆周传播的回音壁模式(Whispering Gallery Mode, WGM)。使用集成光子学方法操控光学涡旋的中心问题，是能量在平面波导密闭光学模式和自由空间光学涡旋模式之间如何耦合。这一耦合过程依赖于在光子结构中嵌入具有圆柱对称性的结构扰动。

基于硅光波导的集成涡旋场发射装置可以通过标准集成电路制造技术制造。这样的集成器件可以产生多种模态的涡旋光束，可以容易地彼此连接以在光子集成电路中形成大而复杂的阵列，并且可以用于通信、传感和粒子操纵等领域。这一突破使得大规模、低成本制造光学涡旋器件芯片成为可能，这将促进许多以前受到限制的新应用的发展。

本文提出一种基于环形谐振器的光学涡旋发射装置，该方法可以输出不同拓扑荷的涡旋光束。本文的工作是基于文献 [12] 的方案。器件的工作波长为1600~1800 nm，通过巧妙设计光栅结构来控制偏振状态，克服了器件固有的高折射率对比度带来的左旋圆偏振(Left-Hand Circular Polarization, LHCP)和右旋圆偏振(Right-Hand Circular Polarization, RHCP)光的叠加问题，得到了高纯度的单一圆偏振标量涡旋光束。

2. 光学涡旋发射装置设计原理

在标量涡旋中，存在拓扑空间相位结构，但偏振不变。例如，圆偏振光学涡旋可以表示为呈现空间变化的涡旋相位态和圆偏振态 [13] 的乘积。如果偏振态具有呈现空间变化的矢量分布，则相应的光场被称为偏振涡旋或矢量涡旋，并且相应的奇异性被称为极化奇异性或矢量正弦 [14] [15] 。与携带OAM的相位涡旋相反，矢量涡旋总是与复杂的自旋角动量(Spin Angular Momentum, SAM)与OAM耦合有关。

光学涡旋发射装置发射的光可以描述为两个正交标量涡旋的叠加，它由拓扑荷为l_TC − 1的LHCP和拓扑荷为l_TC + 1的RHCP光组成，通过调整横向自旋态可以得到高纯度的单一圆偏振标量涡旋光束。

Figure 1. Schematic diagram of the compact optical vortex launcher

图1. 紧凑型光学涡旋发射装置示意图

图1显示了集成光学涡旋发射装置的示意图。准TE模式从接入波导耦合到环形谐振器中，然后激励WGM。通常，由于高折射率波导，侧壁倏逝波中存在局部角向分量Eφ，并且相对于径向分量Er处于正交相位。因此，倏逝场中的局部SAM在z方向上表现出“横向”旋转轴，与WGM的局部传播方向正交。随着亚波长散射体以二阶光栅方式排列，来自WGM倏逝场的一阶衍射光共同产生了一个携带OAM并垂直于谐振器平面的圆柱矢量涡旋光束 [16] 。

圆柱矢量涡旋光束从该结构中发射通常可以用传输矩阵的形式描述为E_out = M₂∙M₁∙E_in。WGM在谐振器周围保持均匀分布，矩阵的输入光为侧壁倏逝波，并且可以在局部径向偏振Er和角向偏振Eφ的基础上表示。以逆时针(Counter-Clockwise, CCW)传播的WGM为例，E_z在侧壁处可以忽略，散射体对WGM倏逝波的扰动由矩阵表示

$M_1=\left[\begin{array}{cc}{W}_{rr}& 0\\ 0& W_{\phi \phi }\end{array}\right]\exp \left[i\delta \left(\phi \right)\right]$ (1)

其中δ(φ) = −qφ是通过二阶光栅散射获得的螺旋相位，q是谐振器周围散射体的总数，W_ii (I = r, φ)是量化散射体对电分量E_i强度的调制的实数。这里定义了受扰倏逝波的局部横向自旋态为

$\sigma =\frac{i\left(E_{rr}{E}_{\phi \phi }^{*}-E_{rr}^{\text{*}}{E}_{\phi \phi }\right)}{{\left|E_{rr}\right|}^2+{\left|E_{\phi \phi }\right|}^2}$ (2)

其中E_ii = W_iiE_i，|σ| ≤ 1且是一个实数，因为E_φφ和E_rr总是在侧壁处彼此正交振荡，并且它直接表征了横向自旋的空间密度 [17] [18] 。这里对于左手旋转的横向SAM，σ > 0，右手旋转的横向SAM，σ ˂ 0。此外，沿着谐振器行进的CCW WGM的矢量场经历了局部坐标(r, φ)相对于全局参考系(x, y)的旋转，如φ∙z，这也可以通过矩阵来描述

$M_2=\left[\begin{array}{cc}\text{cos}\phi & -\text{sin}\phi \\ \text{sin}\phi & \text{cos}\phi \end{array}\right]$ (3)

通过应用传递矩阵M₁和M₂，输出圆柱矢量涡旋光束的琼斯矢量变为

$E_{out}\propto \frac{1}{2}\left\{\sqrt{1+\sigma }{\text{e}}^{i\left(l_{TC}-1\right)\phi }\left[\begin{array}{c}1\\ i\end{array}\right]+\sqrt{1-\sigma }{\text{e}}^{i\left(l_{TC}+1\right)\phi }\left[\begin{array}{c}1\\ -i\end{array}\right]\right\}$ (4)

输出圆柱矢量涡旋光束的拓扑荷满足l_TC = p − q的选择规则，可以通过简单地改变输入波长来调整，使其与不同的环腔谐振一致。

输出圆柱矢量涡旋光束中总角动量的z分量(J_z = L_z + S_z = l_TCħ)与给定的WGM方位角模阶数p和光栅数q保持守恒，而与横向自旋状态无关。圆柱矢量涡旋光束中每个光子携带的SAM和OAM的z分量为

$S_z=\sigma \hslash ,L_z=\left(l_{TC}-\sigma \right)\hslash$ (5)

此外，式(4)中的LHCP和RHCP分别具有l_TC − 1和l_TC + 1的拓扑荷。这种叠加的组成取决于WGM倏逝波的横向自旋态。特别是，当光栅散射体位置处的偏振达到圆偏振态之一(即σ = ±1)时，这种叠加减少为具有单个OAM本征态的单个圆偏振标量涡旋态，即只有一个LHCP或RHCP光。

波导倏逝波中的横向自旋态σ通常取决于倏逝区中角向E_φ和径向E_r场分量iE_φ/E_r的比率，该比率主要由折射率对比度和光的入射角决定，高度受限波导模式中渐逝波的横向自旋也会因横向限制条件而显著改变，特别是波导芯尺寸。通过修改芯中横向分量的模式分布及其在波导边界处的空间导数，可以设计iE_φ/E_r比率的大小 [19] 。换言之，通过调整波导几何结构以及模式的矢量分量，可以调整σ，从而实现倏逝波中的横向自旋操纵 [20] 。

硅被广泛用于集成光电器件的设计材料，其高折射率对波导中的电磁波有更强的束缚作用，同时硅刻蚀工艺也非常成熟，几微米以内的加工误差可以充分保证器件性能。本文提出的光学涡旋发射装置的工作波长设计为1600~1800 nm，通过根据需要改变环的等效半径可以重新设计其工作波长；硅的有效折射率n_eff约为2.8；脊波导宽度为500 nm，高度为470 nm，其中衬底高度为130 nm，用于实现单模操纵，该结构通常用于集成光电器件。

如图2所示，根据其波导截面的电场分布，波导侧壁和顶部的电场分别以角向和径向偏振为主，对于准TE模式，如果在波导的侧壁上刻蚀光栅，散射光束将主要在方位角方向上；相反，如果在波导顶部刻蚀光栅，散射光束为具有径向偏振的电场。

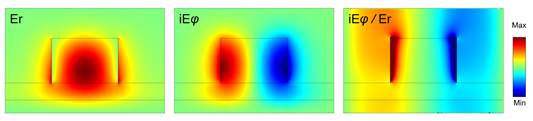
Figure 2. Electric field distribution in the ridge waveguide cross section

图2. 脊波导截面的电场分布

当光在环形波导中传播时，能量被二阶光栅逐渐辐射出来，微环中的能量随之衰减，产生了不均匀的近场强度分布。当光栅耦合系数增加，这种现象会更加明显。方位角方向的振幅变化将产生边模，从而使模式的纯度恶化。对于小半径器件，径向传播波导平面内的光学模式沿径向符合贝塞尔函数分布，二阶圆形光栅应根据沿径向的贝塞尔/汉克尔函数的相位交替进行优化 [21] [22] 。对于大半径器件，圆形光栅可以是周期性的，并且大半径器件也减小了弯曲损耗，因此本文设计了大半径环形波导，其等效半径为6900 nm，光栅元件的个数为72个，光栅周期约为600 nm。

当二阶布拉格光栅的占空比接近0.5时，光栅的辐射效率处于较高状态 [23] ，因此本文设计光学涡旋发射装置的光栅占空比为0.5。

基于上述分析，最终确定环形谐振器等效半径为6900 nm，宽度为500 nm，高度为470 nm，其中衬底高度为130 nm；光栅元件凸出60 nm，占空比为0.5，共有72个分布在环形波导的外侧；接入波导的宽度和高度与环形谐振器一致，接入波导与环形谐振器之间的间隙为50 nm，以保证接入波导与环形波导的有效耦合。

3. 光场性质仿真分析

3.1. 谐振位置

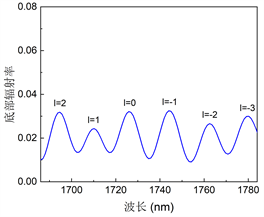
当微环达到谐振状态时，接入波导的透射谱刚好呈现洛伦兹凹陷，每一个谐振位置对应一个器件的辐射峰，如图3(a)和图3(b)所示，给出了该器件的顶部和底部辐射谱线。波长为1693.74 nm，1710.17 nm，1726.92 nm，1743.99 nm，1762.45 nm，1779.18 nm分别对应l_TC = 2，1，0，−1，−2，−3的谐振位置。谱线中相邻两个谐振波长的间距定义为自由频谱范围(Free Spectrum Range, FSR)，该器件的FSR约为17 nm。

通过对比图3(a)和图3(b)，该器件的除了向顶部辐射能量，同时也会向底部辐射一部分能量，一般称之为泄露光，在设计结构时希望尽可能减小这部分能量，中山大学蔡鑫伦等人提出过在谐振器硅膜下方增加金属反射镜的方案 [24] ，反射镜将发射到衬底的光反射回空气，反射光束随后与原始光束发生干涉，产生具有高效率和小发散角的OAM光束。除了上述方法，通过后期对耦合距离、耦合长度的优化，可以进一步提高器件的发射效率。

(a) (b)

Figure 3. (a) Top radiation efficiency; (b) Bottom radiation efficiency

图3. (a) 顶部辐射效率；(b) 底部辐射效率

3.2. 光场截面

OAM光束在自由空间传播时具有一定的发散角，图4显示了器件仿真结果中的光束传播截面图。器件位于y = 0的位置，从截面图可以看到，除了向器件的正上方辐射能量，同时也会向正下方辐射能量，在设计结构时希望尽可能减小下方的辐射能量。随着传播距离的增大，光束的光斑也随之增大，符合OAM光束的发散特性。

3.3. 光场分布

进一步分析器件上方2000 nm处的电场分布。OAM光束的强度可以通过x偏振和y偏振两个方向上的电场能量叠加进行表征，叠加后的能量分布与z偏振方向一致。侧边刻蚀结构对应谐振点的x和y偏振的电场和相位如图5(a)所示。根据光场的复振幅表达式，将其分解为LHCP和RHCP的形式，结果如图5(b)所示。

通过分析仿真结果，辐射光场生成了与RHCP拓扑荷数相同的单个圆偏振OAM光束，这说明RHCP的电场能量远大于LHCP，如图5(b)所示，LHCP在正阶产生了轻微电场能量，而在负阶其能量几乎被完全抑制。光学涡旋发射装置的透射谱在零阶拓扑荷(l_TC = 0)的谐振位置出现了模式分裂现象，这是由于背向散射引起的 [25] 。

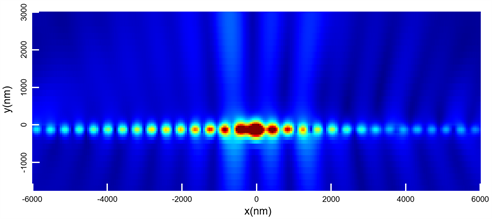
Figure 4. Light field cross-section diagram

图4. 光场截面图

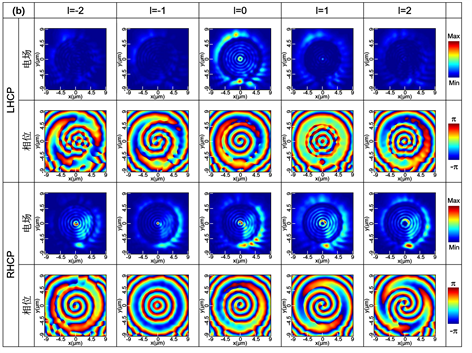
Figure 5. Light field distribution (a) electric field and phase under x and y polarization; (b) electric field and phase of LHCP and RHCP

图5. 光场分布(a) x和y偏振下的电场和相位；(b) LHCP和RHCP的电场和相位

根据设计原理，该器件同样支持从端口2激励，以激发相反的顺时针(Clockwise, CW)模式。当从端口2激励时，与端口1输入结果相反，RHCP的能量被几乎抑制。

4. 结论

总之，本文已经展示了一种基于SOI平台的紧凑型标量光学涡旋发射装置。通过蚀刻在波导外侧的二阶布拉格光栅，几乎完全抑制了LCHP和RCHP中的一个分量，实现了单个圆偏振涡旋分量。仿真结果验证了所提方法的有效性，并表征了该方法的光场和相位特性。光的横向SAM和固有OAM之间的这种直接相互作用为通过SOI实现更复杂的光操纵提供了一条有希望的途径。