1. 引言
现实世界中的很多系统都可以抽象为复杂网络 [1] ,如蛋白质交互网络 [2] 、交通网络 [3] 、科学合著网络 [4] 等。在此类网络中,一般用顶点表示抽象实体,用边表示抽象实体之间的关联。随着复杂网络系统逐渐呈现多样化,挖掘和利用网络信息变的越来越困难。2004年Newman和Girvan首次提出复杂网络具有社区结构的特征 [5] ,为发掘复杂网络数据提供了新的思路。通过利用网络中顶点和边的结构特征,挖掘能够反映现实的网络信息,许多社区发现算法陆续被提出 [6] 。但大多数方法默认每个顶点只能隶属于唯一社区,事实上,真实网络中的顶点会存在多重隶属关系。例如,一个人会与多个社会群体存在关联,如家庭,朋友,同事等,这类问题被称作重叠社区检测问题 [7] 。
复杂网络数据挖掘工作目前遇到的主要挑战之一,就是识别更接近现实世界的重叠社区。截至目前,已经被提出来的用于重叠社区检测的算法大致可以分为五类。第一类方法是基于团渗透理论的算法,如CPM [8] 算法,谱分析聚类算 [9] ,非负矩阵分解法 [10] 等。此类方法类似于模式识别的方法,旨在发现网络特定的局部结构,但上述方法都需要预先给定社区数目,且对于大规模网络算法时间复杂度较高。第二类是基于链接划分的算法,Ahn等人于2010年提出基于边相似性的层次聚类算法 [11] ,层次聚类算法通过计算顶点对间的相似性并创建带有层次的聚类树,然后对聚类树进行划分。虽然此类通过链接划分的方法看起来很直观,但基于链接的划分的算法将社区定义为模糊的,所以在划分质量上并不能得到合理的论证。第三类方法是基于模糊检测的算法 [12] ,不难发现重叠社区的定义与模糊集的定义十分相似,即每个元素对多个集合都有一定的隶属度。基于模糊思想的算法问题在于需要确定隶属向量的维数,将该值作为参数传递给算法,因此在计算过程中较为复杂。第四类方法为基于局部扩展的算法 [13] ,首先随机选择初始的种子顶点,然后构建适应度函数,将最优适应度函数的顶点添加到社区中,反之将其移除,反复进行此过程,直至不能进一步优化划分结果。第五类方法为标签传播算法,如COPRA [14] 、SLPA [15] 等,此类算法通过更新邻居顶点标签来改变社区的标签,此类算法减少了运行时间但形成的社区结果不稳定。
以上描述的五类算法适用于不同的网络,但随着互联网的飞速发展,网络的规模也在飞速扩张,顶点间的关系也表现的越来越复杂,这使得算法运行时间的增加,划分的结果变差。因此,本文提出一种基于社区密度的重叠社区检测算法(Community Density Based Overlapping Community Detection Algorithm, CDOCD)。首先通过社区密度函数和阈值确定候选社区,然后引入社区间相似性的概念作为合并候选社区和现有社区的判断条件。本算法不仅考虑了网络的结构特征,且在判断过程用使用单一阈值,在减少运行时间的前提下提高了划分精度。在两类人工合成网络上进行了充分的测试,并与其它重叠社区检测算法进行了比较,在扩展的标准化互信息和时间复杂度上都呈现出良好的算法性能。
2. 预备知识
从数学的角度,复杂网络可以表示为一个图
,其中
表示顶点的集合,
表示所有边的集合。其中
和
为图中顶点数和连边数。进一步,用
表示任意
的邻居顶点集。
定义1 (社区间相似性)给定图G及任意两个社区
,定义社区
之间的相似性为
, (2-1)
其中
表示
两个社区中相同元素的个数,
表示两个社区中不重复出现的总元素个数。
定义2 (社区内密度)对于任意社区C,其社区内密度定义为
, (2-2)
其中
表示社区C的内部度数和,即社区内部连边数,
表示社区C的顶点数目,
用于衡量社区内部联系紧密程度,取值范围在
之间,
越大表示社区C内部联系越紧密。
定义3 (社区外密度)对于任意社区C,其社区外密度定义为
, (2-3)
其中
表示社区C外部度数和,即社区内顶点与社区外顶点连边数,
用于衡量社区外部联系紧密程度,取值范围在
之间,
越大表示社区C内部联系越稀疏。
定义4 (社区密度)对于任意社区C,社区密度定义为
, (2-4)
其中
用于评估社区总体紧密程度,取值范围在
之间,
越大表示社区质量越高。
社区实质上是由顶点和边组成的一个具有共同性质的顶点集合,集合内部顶点联系紧密,不同集合之间联系稀疏。因此在最大化
和最小化
寻找一个平衡,是社区发现算法的目标。在本文中我们
和阈值来判断生成社区的质量,在很大程度上提高了社区划分结果的质量。
3. 基于社区密度的重叠社区检测算法
本节主要介绍基于社区密度的重叠社区检测算法,具体工作分为如下部分:重叠社区检测算法的构建和对该算法时间复杂度的分析。算法构建部分,我们主要从领域扩展和社区合并两个层面加以说明。
3.1. 算法构建
我们将CDOCD算法分为邻域扩展和社区合并两个主要阶段。首先在邻域扩展阶段我们将邻居顶点视为最佳候选顶点,通过邻居顶点间的交集运算确定候选社区,且候选社区密度要不小于给定阈值t以确保生成的候选社区的质量。然后进入社区合并阶段,在此阶段我们将生成的候选社区与现有社区进行合并。为确保合并后的社区是联系紧密且相似的,合并的两个社区其社区间相似性也要大于阈值t,并将合并后的社区作为新的候选社区继续进行迭代。在算法两个阶段中我们都采用的唯一阈值,这样可以避免重复定义阈值增加算法的复杂度。
算法1为基于社区密度的重叠社区检测算法的第一阶段,即邻域扩展阶段。在此阶段通过邻居顶点间的交集运算确定候选社区,考虑了网络的结构性质,并利用社区密度和阈值确保生成社区的质量。此过程迭代进行,直至社区划分结果不满足更新后的社区密度和阈值。
算法1 基于社区密度的重叠社区检测算法(邻域扩展阶段)
输入:图数据
,阈值t,其中
。
输出:重叠社区集合
。
过程:
1、计算顶点集V中所有顶点v的邻居顶点集
;
2、计算邻居顶点
的邻居顶点集
,其中
;
3、将
和
的交集作为候选社区
;
4、根据公式(2-4)计算此时社区密度
,并要求
不小于当前阈值t;
5、更新此时的社区集合C、候选社区
、阈值t。
显然,在算法1中生成的候选社区并不是最终的社区划分结果,需要进行社区合并扩展候选社区生成最终的重叠社区集合。算法2为基于社区密度的重叠社区检测算法的第二阶段,即社区合并阶段。在此阶段我们讨论了候选社区
和现有社区
合并的几种情况,其中
。
算法2 基于社区密度的重叠社区检测算法(社区合并阶段)
输入:候选社区
,阈值t,其中
。
输出:重叠社区集合
。
过程:
1、若候选社区
是现有社区
的子集或者等于现有社区,则返回社区列表C;
2、若现有社区
是候选社区
的真子集,则将
从社区列表C中移除;
3、候选社区
不是现有社区
的子集或超集,根据公式(2-1)计算候选社区
与现有社区
间的相似性,其中
;
4、若候选社区与现有社区间相似性大于阈值,合并两个社区生成新的候选社区
;
5、根据公式(2-4)计算更新后候选社区密度,若此时候选社区密度
不小于阈值;
6、将新的候选社区
添加至重叠社区集合C。
在社区合并阶段我们将候选社区与现有社区合并生成新的候选社区,然而两个相似度较低的社区合并会生成较大的且相关性的较低社区,或者会丢失部分小的社区,从而降低社区划分精度。因此新的候选社区的社区密度要不小于阈值t,并且为保证合并后的社区内部联系是紧密且相似的,合并的两个社区间相似性也要大于阈值t。相似性的阈值沿用社区密度阈值t,这种方法可以避免重复定义阈值,减少算法的复杂性。
3.2. 算法复杂度分析
在本节我们对CDOCD算法的时间复杂度给出具体分析。给定一个顶点数为n,边数为m的图G,平均每个顶点有
条边,因此遍历顶点和邻居顶点耗时为
。算法通过集合运算生成社区,为线性时间,运行的平均时间为
。社区密度是通过遍历候选社区的顶点进行计算的,而候选社区是由两个顶点的邻居顶点的交集所形成的,所以候选社区的元素的平均个数为
,因此在社区密度函数上运行的时间为
。社区合并阶段需要遍历所有社区通过子集运算查找两个集合的相同元素,社区个数为
,因此社区合并阶段的运行时间为
。综上,对所有顶点及其邻居顶点重复以上时间,需要遍历
次,所以
为算法总运行时间。
4. 实验分析
在现实世界中,许多数据的获取是有一定困难的,或者获取的数据集真实划分是不确定的,因此可以通过合成数据进行检验和评估算法的有效性。比如广被接受的重叠图生成器OCG [16] 和LFR [17] ,在本节我们通过人工生成数据对算法进行测试,选择可用于重叠社区评估的归一化互信息检验算法精度。
4.1. 评估指标
用于比较算法性能的方法很多,本文采用了扩展到重叠社区的归一化互信息 [18] ,数学上表示为
, (4-1)
其中
表示
中的顶点数,
表示社区
中出现在真实社区
中的顶点数,
表示检测到的社区数,
表示实际社区数。NMI取值范围为
,其中1表示检测到社区与实际社区结构完全一致。
4.2. 算法性能评估
由第3节可知,阈值的选择是确保算法成功的关键,因此在与其他算法进行比较之前,通过改变OCG网络和LFR网络的参数来评估阈值对算法精度的影响。
4.2.1. 改变人工合成网络参数评估阈值对算法精度的影响
 (a) (b)
(a) (b)
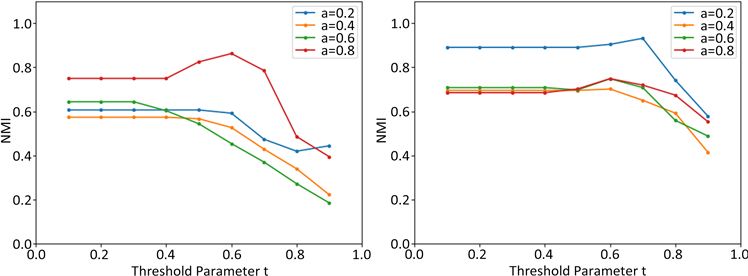
Figure 1. Variation of algorithm accuracy with threshold value for changing OCG network parameters
图1. 改变OCG网络参数算法精度随阈值的变化
在图1(a)中,我们设置OCG网络的社区个数i为10,每个社区的平均顶点数a为100,重叠比率ε为0.3,连接比率λ为0.3,固定社区外密度ω为0.2,调整社区内密度α从0.2至0.8。我们发现算法精度随着社区内密度的增加而增加,并且只要阈值参数的上界是社区内密度,就能够得到较高的NMI评分。图1(b)的OCG网络其他参数不变,固定社区内密度α为0.8,调整社区外密度ω从0.2至0.8,我们发现算法性能随阈值t的增加而下降,并且随着ω的增加,算法精度下降,这是由于随着社区密度外密度的增加,社区密度减小,伴随着阈值的提高,候选社区无法满足此时的社区密度,许多顶点无法得到正确的划分,使得算法性能下降。

Table 1. LFR network parameters setting
表1. LFR网络参数设置
 (a)(b)(c)
(a)(b)(c)
Figure 2. Variation of algorithm accuracy with threshold value for changing LFR network parameters
图2. 改变LFR网络参数算法精度随阈值的变化
图2(a)为表1中的
网络算法精度随阈值参数的变化。可以看出随着μ的增大,算法性能下降,但不明显。首先阈值在0到0.4时算法性能稳定,然后随着阈值的增加算法性能下降。这是因为社区合并阶段,我们依据阈值来判断两个社区间的相似性,而过高的阈值,会导致许多社区无法进行正常的合并,从而降低了算法精度。图2(b)为
网络算法精度随阈值参数的变化。我们设置重叠顶点
由200至500,步长为100。随着重叠顶点数目增加算法性能下降,但相对稳定,说明该算法可以很好的适用于重叠社区的划分。图2(c)为
网络算法精度随阈值参数的变化。我们设置重叠社区资格数
由2至6,步长为2。可以看出随着
的增加算法性能下降,这是因为随着顶点隶属社区数目增加,在社区合并阶段部分此类顶点无法得到正确的划分从而导致算法精度下降,但可依照经验根据数据类型改变阈值来提高划分精度。
通过上述实验可以看出,如果一个社区内部联系紧密,外部联系稀疏,通常选择较大的阈值,反之则选择较低的阈值。对于大型网络,我们可以通过提取随机社区获取他们的平均社区内外密度。对于小型网络,可以利用算法在一定阈值范围内进行运行选择合适的阈值。
4.2.2. 对比算法实验
为了进一步验证算法的有效性,我们将CDOCD算法和COPRA、NISE [19] 和CPM算法进行了比较。选择以上算法的原因如下:CORPA算法是一种基于标签传播的重叠社区检测算法,在应用上和结果的准确性上与CDOCD算法相似,NISE是通过贪婪方法拓展种子节点生成社区的方法,比较新的且有效的算法之一,CPM算法,是一种通过派系来识别网络社区结构的算法,是重叠社区检测最常见的方法之一。
 (a)(b)(c)
(a)(b)(c)
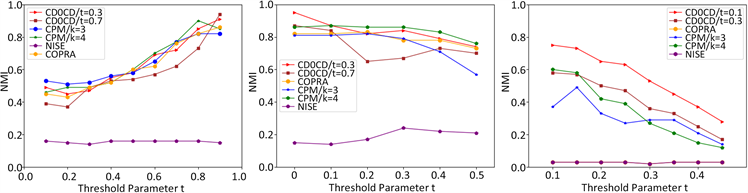
Figure 3. Comparison of algorithm accuracy under different networks
图3. 不同网络下算法精度对比
在图3(a)中,我们设置OCG网络社区个数i为10,每个社区的平均顶点数a为100,重叠比率ε为0.3,连接比率λ为0.3,固定社区外密度ω为0.2,增加社区内密度α由0.1至0.9,步长为0.1,在该数据下每种算法运行30次取NMI均值。可以看出CDOCD算法同其他算法的性能都随着社区内密度的增加算法性能提高,表明网络内部联系越强算法性能越佳。图3(b)中其他参数保持不变,固定社区内密度α为0.8,增加社区外密度ω由0至0.5,步长为0.1。在该数据下每种算法运行30次取NMI均值,通过此实验同样验证了,通过优化社区密度能够提高社区划分精度。图3(c)我们设置LFR网络顶点数
,重叠顶点数
,重叠社区资格数
,增加混合参数μ由0.1至0.45,步长为0.05。在该数据下每种算法运行10次取NMI的均值,可以看出每种算法随着μ值增加算法性能下降,但CDOCD算法性能优于其他算法。
4.3. 算法时间复杂度对比
在本节主要对比CDOCD算法与CPM算法、COPRA算法、NISE算法的时间复杂度。
如表2所示,CDOCD算法时间复杂度为
,为多项式时间,在大多数图中网络的边数大于顶点的数目,因此CDOCD算法,通过边来主导运行时间;CPM算法的时间复杂度主要取决于网络的规模和社区结构两个因素。假设网络中有个节点,m条边,k个社区,CPM算法的时间复杂度为
。在实际应用中,CPM算法需要通过不断的搜索、扩展和组合来获取所有大小为k的团,并且k的取值与网络的规模有关,当k较大时,算法的运行时间也就会相应地增加。综合来看CPM算法时间复杂度较高,适用于网络规模较小而且社区结构比较简单的情况 ;COPRA算法通过给每个顶点设置标签列表解决LPA [20] 算法随机不稳定的问题。算法的时间复杂度主要取决于两个因素,标签传播迭代的次数和每个节点的邻居节点数。具体时间复杂度为
,其中T是迭代次数,D是平均节点度数,N是节点数量。在实际的实验过程中,通常需要几十次迭代就能让大部分节点归属于一个社区,并且具体运行时间还取决于具体数据集的大小和稠密程度,综合来看该算法具有较快的运行速度,然而算法会随着网络规模的增加迭代时间加长,结果随机性也会随之增强;NISE算法主要包括种子扩展和邻居节点加权两个步骤,其时间复杂度主要与网络规模和算法参数有关。种子扩展阶段耗时
,其中k为种子数量,
为每个种子扩展的最大层数,n为网络节点数。对邻居节点加权耗时
,其中
为每个社区邻居节点选择的最大数量。该步骤的时间复杂度与种子扩展的时间复杂度相近因此NISE算法的总时间复杂度为
,其中L为扩展的最大层数,k为种子数量。NISE算法在大型网络上运行稳定性表现良好,但其运行步骤较多更加耗时,综合来看CDOCD算法在运行时间上表现良好。

Table 2. Algorithm time complexity comparison
表2. 算法时间复杂度对比
5. 结论
本文提出一种基于社区密度的重叠社区检测算法CDOCD,一方面,通过设置单一阈值
作为算法的判断条件,减少算法的运行时间;另外我们将算法分为两个阶段,在每个阶段都将社区密度作为候选社区的生成条件确保社区划分的质量,提高了划分精度。并在两类人工合成网络上进行严格的实验,实验结果表明本文提出的算法在计算效率和社区划分质量上优于其他算法。在未来,我们将该算法应用于各类复杂网络真实数据以及大型网络数据上,更加高效且高质量地获取网络的信息。
基金项目
国家自然科学基金资助项目(61966039)。