1. 引言
粗糙集理论 [1] [2] 是一种处理不精确、不一致信息的有效数学工具,具有极为广泛的应用场景,目前已经成功应用于智能工业 [3] [4] 、图像处理 [5] [6] 、智能决策 [7] 等多个领域。
属性约简 [8] [9] 是粗糙集理论研究中的关键课题之一。属性约简的核心思想是在保持分类能力不变的前提下,删除冗余属性,从而实现海量数据的有效降维。基于贪心策略的启发式算法是获取属性约简的主要方法之一。传统的启发式属性约简算法效率较低,难以有效地处理大规模数据,为了进一步提高算法的约简效率,许多学者从多种角度对启发式算法的加速机制展开了研究。Qian等 [10] 提出了正向近似的加速策略,通过在算法迭代过程中逐步删除正域的方式,有效提高了算法效率。陈曼如等 [11] 从样本和属性的视角出发,通过减少正域样本和算法的迭代次数,设计了基于正区域不变的快速属性约简算法。赵立威等 [12] 在序决策系统下通过优化启发式算法中的属性添加策略,构建了基于特征粒的快速约简算法。Chen等 [13] 从对象、属性和粒度视角设计了基于决策系统全部分类的加速机制,提出了基于融合加速机制的通用属性约简加速算法框架。
以上算法都是针对决策系统中全部决策类进行属性约简,但在实际应用中,决策者往往对某一个或多个特定类决策类更感兴趣。为此许多学者针对特定类的属性约简问题展开了研究并取得了很多优秀的研究成果。Liu等 [14] 在多种约简目标下建立了基于差别矩阵方法的特定类属性约简,为局部属性约简提供了新的思路。Zhang等 [15] 从信息论和代数角度分析了全部决策类与特定类约简之间的层次联系。Wang等 [16] 在邻域决策系统中,针对特定类提出了局部条件熵的定义,并设计了基于条件熵的局部属性约简算法。
虽然有大量学者针对启发式算法进行了优化,但在多特定类的属性约简研究中,现有的经典启发式属性约简算法仍存在效率较低的问题,难以有效处理大规模数据。针对该问题,本文从多特定类的视角出发,提出了多特定类正域约简的定义,并结合对象、属性和粒度的加速方法,设计了基于组合加速机制的多特定类快速正域约简算法,并通过实验验证了所提算法的有效性。
2. 基本概念
给定一个Pawlak决策系统
,其中,U为对象集合,称为论域,C和D分别为条件属性集和决策属性集。
表示对象
在属性
上的取值。例如表1所示的Pawlak决策系统中,论域
,条件属性集
,决策属性
。

Table 1. Pawlak decision system
表1. Pawlak决策系统
定义1 [1] 给定一个决策系统
,对于
,定义A上的不可区分关系为:
.
是一个满足自反、对称和传递的等价关系,根据等价关系
可导出论域上的一个划分
,其中,
表示对象
关于属性集A的等价类,为方便表示,
可简记为
。基于决策属性D对论域形成的划分为
,称为决策类集合,集合
(
)称为多特定类。下面给出多特定类
上下近似的定义。
定义2 [1] 给定一个决策系统
,
,对于
,多特定类
关于属性集
A的上下近似集合分别为:
,
.
基于上下近似的概念,以多特定类
为目标概念,通过粗糙集理论可以将论域划分为正域、边界域和负域,定义分别为:
,
,
.
由于
且
,因此多特定类具有良好的扩展性,多特定类既可以包含一个决
策类也可以包含多个甚至全部决策类。
3. 多特定类正域约简
在实际应用中,决策者往往更偏好于某一个或多个特定决策标签的有效知识提取,本节将介绍多特定类正域约简的相关概念和算法。
定义3给定一个决策系统
,
,
,对于
,属性a的内部属性重要度为:
.
定义4给定一个决策系统
,
,
,对于
,属性a的外部属性重要度为:
.
内部属性重要度可以用来评估属性是否冗余,常用于求核和去冗余操作。外部属性重要度往往用于迭代过程中的最佳属性选择。
定义5给定一个决策系统
,
,若
为多特定类
的正域约简,则满足如下条件:
1)
;
2)
,
。
其中,条件1)保证了约简前后多特定类正域不发生变化,条件2)则保证了约简属性集中的任一属性都是必要的。基于正向贪婪的多特定类启发式属性约简算法如表2所示。该算法的流程图如图1所示。
在算法FGARM中,Step1为初始化过程;Step2为迭代选取属性的过程,根据外部属性重要度对属性进行评估,每次选择一个最佳属性添加至约简属性集中,直到满足中止条件为止;Step3和Step4为去冗余和输出约简的过程。

Table 2. A forward greedy heuristic attribute reduction algorithm for multi-specific decision classes (FGARM)
表2. 基于正向贪婪的多特定类启发式属性约简算法
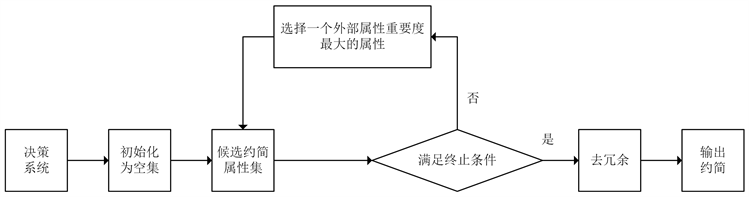
Figure 1. A flow chart of FGARM algorithm
图1. 算法FGARM流程图
4. 多特定类快速正域约简
算法FGARM在计算约简时存在待处理对象规模较大、属性迭代次数过多和待评估属性数目较多等问题,难以高效处理大规模数据。为进一步提高多特定类的约简效率,本节从对象、属性和粒度三个方面分析了多特定类启发式算法的加速机制,提出了基于组合加速机制的多特定类快速正域约简算法。
定理1给定一个决策系统
,
,
,对于
,满足:
,
其中,
。
定理1表明,随着属性的增加,边界域中的部分样本会被精确划分至正域,因此可以通过删除正域和负域的方式实现多特定类的对象加速。当所选多特定类为全部决策类时,此时负域为空集,此时算法退化到文献 [10] 中的情况,每次迭代过程中仅删除正域中的对象。
定义6给定一个决策系统
,
,属性集
,
,对于
,若
且满足
,
,
,
,
,
则称
为属性
的属性组。
定义6为属性组的定义,在启发式算法的迭代过程中,可以通过构造属性组的方式向约简属性集中一次添加多个属性,降低算法的迭代次数,实现多特定类的属性加速。同时,通过差集运算,有效地避免了部分冗余属性的存在。
定义7给定一个决策系统
,
,
,多特定类
关于属性子集A的局部粒度为:
,
其中,
。
定义7为局部粒度的定义,由于负域中的对象与多特定类中的决策规则无关,因此可以仅利用正域和边界域中的样本对局部粒度进行定义。属性的局部粒度值越大,则该属性对多特定类样本的区分能力越弱,在属性评估过程中,可以通过忽略一些粒度较粗的属性以降低待评估的属性规模,实现多特定类的粒度加速。当所选多特定类为全部决策类时,此时负域为空集,则局部粒度退化到文献 [13] 中的全局粒度定义,此时粒度可用于表示属性对决策系统中所有样本的区分能力。
通过上述定义,可以在启发式算法中设计基于对象、属性和粒度的多特定类组合加速机制,提高算法的约简效率。下面给出基于组合加速机制的多特定类快速正域约简算法,如表3所示。该算法的流程图如图2所示。

Table 3. A fast attribute reduction algorithm for multi-specific decision classes positive region based on fusing acceleration mechanism (FARAM)
表3. 基于组合加速机制的多特定类快速正域约简算法
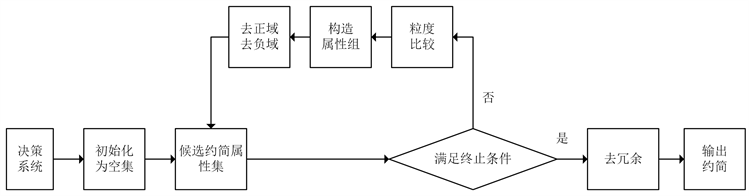
Figure 2. A flow chart of FARAM algorithm
图2. 算法FARAM流程图
在算法FARAM中,Step1为初始化过程;Step2为计算各属性的局部粒度值,用于后续迭代过程中的粒度比较;Step3为迭代选取属性的过程,其中,Step3.1~Step3.3为粒度比较以降低待评估属性数目,Step3.4~Step3.5为构造属性组实现属性加速的过程,Step3.6为删除正域和负域实现对象加速的过程;Step4和Step5为去冗余和输出约简的过程。
相比于算法FGARM中,算法FARAM的优势为:
1) 算法FARAM在每轮迭代过程中通过删除正域和负域的方式实现对象加速,大幅降低了算法的扫描空间;
2) 算法FARAM在每次迭代过程中通过构造属性组的方式,一次添加多个符合要求的属性至候选约简属性集中,有效减少了算法的迭代次数;
3) 算法FARAM通过粒度比较的方式,忽略了部分粒度较粗、分类能力较弱的属性,有效降低了迭代过程中待评估的属性规模。
5. 实验分析
本节将算法FARAM、FGARM和算法FSPA-PR [10] 、FARA [13] 分别进行了对比。其中,算法FSPA-PR和FARA均为针对决策表中的全部决策类进行属性约简。实验对比分为两部分:第一部分为算法约简长度的对比;第二部分为算法约简效率的对比,从对象、迭代次数和约简时间三个方面进行了对比分析。
实验所采用的6组数据集信息如表4所示。实验环境描述如下:Windows 10 (64 bit)操作系统,Inter Core i7-10750H (2.60 GHz)处理器,16 GB内存,所有算法均采用PyCharm 2020软件和Python语言进行测试。由于算法FARAM、FGARM均适用于多个特定决策类,实验过程中在各数据集中选取某些特定决策类进行测试,表中各数据集选定的多特定类决策值集合分别为:{1}、{1,2}、{1,2}、{1}、{0,1,2}和{1,2,3}。
5.1. 约简长度对比
表5为四种算法的约简长度对比。从表中可以看出,相比于算法FSPA-PR、FARA,算法FARAM和FGARM在6组数据集上均可获得相对较短的约简结果。相比于决策系统的全部分类,多特定类的正域规模较小,因此约简结果也相对较短。同时,由于算法FARAM在迭代过程中一次添加多个属性且忽略了部分粒度较粗的属性,属性的添加并不严格遵守属性重要度的大小排列顺序,因此其约简长度要略高于算法FGARM。比如在平均约简长度中,算法FARAM的约简长度为12.3,略高于算法FGARM的约简长度11.5。

Table 5. The length of reduction comparison
表5. 约简长度对比
5.2. 约简效率对比
本节从迭代次数、参与迭代的对象规模和约简时间三个方面进行了对比分析。
表6为四种算法的迭代次数对比。从表中可以看出,基于组合加速机制的算法FARA和FARAM的迭代次数相对较低。例如在数据集Landsat中,算法FARA和FARAM的迭代次数均为1,而算法FSPA-PR和算法FGARM的迭代次数分别为12和8;在数据集Thyroid中,算法FSPA-PR的迭代次数为0,这是由于该算法以核属性作为约简起点,且核属性为约简结果,因此不需要参与迭代。同时,由于算法FARA针对决策系统中的全部分类进行约简,容易找到符合条件的属性构造属性组,因此算法FARA的迭代次数的迭代次数要略低于算法FARAM。比如在平均迭代次数上,算法FARA的平均迭代次数为1.6,而算法FARAM的平均迭代次数为5.0。
表7为算法FARAM在前四次迭代过程中所需处理的对象数目,其中“—”表示算法迭代结束,不需要处理任何对象。由于算法FGARM不具有任何加速机制,每次迭代都需要对论域中的全部对象进行处理,因此在表中仅表示了算法FARAM迭代过程中所需处理的对象数目。从表中可以看出,随着算法迭代次数的增加,算法FARAM会逐步地删除正域和负域中的对象,因此所需处理的对象规模也会逐步降低。若相邻两次迭代所需处理的对象数目相同,则表明该轮迭代中构造的属性组仅包含一个属性且该属性对于构造正域没有任何贡献,如数据集Penbased的第一轮和第二轮迭代,数据集Coil2000的第三轮和第四轮迭代,对象数目均没有发生改变,说明该轮迭代中选择的单个属性对于粒度的划分并无贡献。

Table 7. The number of handled objects in iterations
表7. 迭代中所需处理的对象数目
图3为四种算法的约简时间对比。其中,横坐标为论域规模,纵坐标为算法的运行时间,单位为秒(s)。从图中可以看出,当数据规模较小时,四种算法的运行时间都很低,但随着数据集规模的不断扩大,四种算法的运行时间都随之增加。但是算法运行时间与论域规模并不具有严格的正相关性。比如在数据集Vehicle中,当论域规模由6增至7时,算法FGARM的时间反而有所降低。这是由于该算法为贪心算法,所选择的均为局部最佳属性,该属性仍有部分可能为冗余属性,因此会出现规模增加但运行时间反而减少的情况。对比四种算法发现,算法FARAM的运行时间始终保持最低,且增加幅度较小,稳定性较强。这是由于算法FARAM从对象、属性和粒度三个方面设计了加速机制,从多维度保证了算法的高效性,因此可较大幅度地降低约简时间。
6. 结论
在多特定类正域约简中,启发式属性约简算法虽然能够快速地获取决策系统的一个约简结果,但因其在迭代过程中需要处理全部的对象和属性,而且每次迭代仅选择一个属性,所以当数据规模较大时约简效率仍然较低。本文在启发式算法的基础上,设计了基于对象、属性和粒度视角的多特定类加速方法,提出了基于组合加速机制的多特定类快速正域约简算法,通过删除正域和负域、构造属性组和粒度比较的方法,降低了参与迭代的对象规模、待评估的属性规模以及算法的迭代次数,从而提高了多特定类的约简效率。同时,由于本文在构造属性组和粒度比较的过程中,弱化了属性重要度的利用,因此约简结果可能存在冗余属性较多的情况,进一步地提高去冗余的效率是未来的研究工作之一。
基金项目
本文受烟台市科技计划项目(编号:2022XDRH016)的资助。