1. 引言
在碳酸盐岩油藏钻采过程中很容易因微粒沉积造成井筒附近储层受到污染,从而导致油气产量降低。酸化是解除近井污染常用的措施 [1] [2] [3] [4] ,注入的酸会与岩石发生反应形成一些具有高导流能力的通道 [5] ,从而达到解除污染的目的。在裂缝型碳酸盐岩储层中,酸化不仅能够解除近井污染,而且还能沟通裂缝,增大酸化作用的距离。天然裂缝的渗透率远大于基岩的渗透率,注入的酸在裂缝的引导下进入地层深处,从而使地层的渗透性增加,因此裂缝的分布在一定程度上会主导流体的流动,从而影响碳酸盐岩酸岩反应的溶蚀结构。
在裂缝型碳酸盐岩中,常用的酸岩反应流模型大致可以分为四类,即单裂缝模型 [6] [7] [8] [9] [10] 、裂缝网络模型 [11] [12] 、拟裂缝模型 [13] [14] 以及离散裂缝模型 [15] [16] [17] [18] 。在单裂缝模型中,仅仅对单条裂缝中的流体流动进行了研究。裂缝网络模型忽略了酸液在基岩内的流动。对于拟裂缝模型,裂缝是被看作为是具有高孔隙度以及渗透率的基岩。这类模型对网格尺寸要求较高,当裂缝密度较大时会大大增加计算量。无法处理实际油藏中出现的复杂裂缝。离散裂缝模型采用非结构化网格技术剖分较复杂的裂缝,其剖分过程比较复杂和繁琐。
为了实现对复杂裂缝的高效处理,嵌入式离散裂缝模型就被提出来了。嵌入式离散裂缝模型最早是由Lee等人 [19] [20] 提出,为了提高天然裂缝建模的精确程度。该模型在划分网格时,不需要考虑内部的裂缝形态,降低了网格划分的复杂度,提高计算效率。本文基于嵌入式离散裂缝模型建立裂缝型碳酸盐岩反应流模型,并对该模型进行求解,研究天然裂缝对蚓孔生长动态的影响。
2. 数学模型
裂缝型碳酸盐岩反应流模型主要是由达西尺度模型和孔隙尺度 [21] 两部分组成。达西尺度模型主要用于描述流体的流动、传输以及酸岩反应中孔隙度的变化。孔隙尺度用于描述酸岩反应中岩石物性参数随着孔隙度的变化。本文研究的是裂缝型碳酸盐岩,达西尺度模型与孔隙尺度模型主要由基岩系统和裂缝系统两部分组成,二者之间存在着流量交换,达西尺度的基岩系统和裂缝系统方程可表示如下:
裂缝系统方程:
(1)
(2)
(3)
基岩系统方程:
(4)
(5)
(6)
(7)
式中,上标f为裂缝系统;上标m为基岩系统;
,
分别表示裂缝系统和基岩系统的达西速度向量;
为基岩系统的渗透率张量,
表示裂缝系统的渗透率张量;μ表示流体的粘度;P表示压力;ϕ表示孔隙度;t表示时间;b表示裂缝的开度;
表示为酸在液相中的浓度;
表示为酸在液固表面的浓度;
表示基岩中的有效扩散张量;
表示裂缝中扩散系数;
表示传质系数,即表示在孔隙内酸液从液相传输到液固界面的速度;
表示为比表面积;
表示表面反应速度;
表示酸溶解能力;
表示岩石密度;
表示将基岩和裂缝网格连接起来的窜流函数,表示从裂缝流向基岩,
表示表示从基岩流向裂缝系统。其公式如下:
(8)
式中,
。CI用于表示基质与裂缝之间的连通性指数,
其中
表示基质单元(i, j)与裂缝段k交接面面积,
表示基质单元(i, j)与裂缝段k之间的平均距离。
孔隙尺度方程:
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
式中,下标0表示对应参数的初值;
表示孔隙尺寸迂曲度的分形维数;
表示迂曲度的分形维数;
表示欧拉空间的维数,本文只研究二维问题,其取值为2;
表示最大孔隙直径;
表示最小孔隙直径。本文在数值计算时取
的值取为0.01,其取值方式与刘丕养等人 [21] 的一致。K0初始平均孔隙半径;K表示渗透率;
表示平均孔隙半径;
表示初始孔隙度;
表示初始比表面积;Sh表示舍伍德数;
表示孔隙的渐进舍伍德数;rp为孔隙半径;
表示平均孔隙半径;在本文模拟中
的取值是3.66;Rep表示孔隙的雷诺数,公式可表示为
,u表示酸液的速度;v表示动力学粘度;Sc表示施密特数,定义为
,其中
为动力速度;
表示分子扩散系数;
表示与孔隙结构有关的常数,在本文中取0.5;
、
分别表示二维直角坐标系中,沿坐标系轴y方向和坐标系轴x方向的扩散系数;
表示达西速度的模;
表示孔隙直径;
表示分子扩散系数,用来表示由于分子运动产生的溶质运移;
裂缝中的扩散系数;
表示系数的常数,在本文计算时中取值为0.5。
3. 定解条件
边界条件:
(19)
式中,
表示流体在流动方向上的单位向量;
表示酸注入的速度。
(20)
式中,
表示注入酸浓度。
(21)
式中,
的值为常数。
(22)
(23)
初始条件:
(24)
4. 无因次模型
将上述方程进行无因次化处理。无量纲的变量定义如下:
式中,L表示流体在流动方向上的特征长度,本文取值为岩心长度;x,y表示在直角坐标系中的坐标参数;下角标D表示无因次;Um、Uf分别表示基岩系统和裂缝系统中的无因次速度;km、kf分别表示基岩系统和裂缝系统中的无因次渗透率;
表示西勒模数,定义为反应速度与扩散速度在初始孔隙体积下的比值;Da表示达摩克莱尔数;
表示酸化能力常数,表示为单位体积的酸所溶解的固体体积;
表示轴向配克莱数。
上述方程无因次形式可以表示如下:
(25)
(26)
(27)
(28)
(29)
(30)
(31)
(32)
(33)
边界条件和初始条件:
(34)
(35)
(36)
(37)
(38)
(39)
(40)
5. 模型求解
本文采用顺序法对上述在方程(25)~(31)进行求解。首先通过(25)、(26)、(31)方程,求解得到t时刻的压力分布;然后根据等式(27)、(28)将计算得到t时刻的速度场,最后通过计算(29)、(30)方程,计算t + 1时间步注入酸浓度和孔隙度的分布。在求解物质平衡方程时,采用算子分裂法把它分为两部分:(1)只考虑流动不考虑反应;(2)只考虑反应不考虑流动。这两部分在基质中都需要考虑,而在裂缝中只考虑流体的流动,因为酸液在裂缝流动很快,酸液在裂缝中的反应忽略不计。
(41)
(42)
6. 结果分析
数值模拟中所用的数据如表1所示,表中总结了在本文数值模拟中所使用的参数。除非另有说明,否则所有的值在整个研究过程中都保持不变。


Table 1. List of values of parameters used in simulation
表1. 数值模拟中用到的参数值
6.1. 裂缝对酸岩反应溶蚀动态的影响
6.1.1. 裂缝对溶蚀模式的影响
在酸岩反应中,酸的注入速度对蚓孔扩展有很大影响,不同的注入速度会产生不同的溶蚀模式。本小节通过将酸液以不同的速度,注入到裂缝型碳酸盐岩和非裂缝碳酸盐岩岩心,研究天然裂缝的存在对岩心酸化溶蚀模式的影响。模拟中所使用的参数如表1所示。通过对比有无裂缝情况下酸蚀岩心形成的溶蚀模式,分析不同注入速度下,天然裂缝存在对于蚓孔扩展的影响。数值模拟的结果如图1 所示。图1中(A)列表示不考虑裂缝存在的条件下生成的溶蚀模式,(B)列表示考虑裂缝存在的条件下生成的溶蚀模式,从(a)到(e)注入速度由低到高所对应的溶蚀模式,分别为面溶蚀、锥形溶蚀、蚓孔溶蚀、分枝蚓孔以及均匀溶蚀,这个结果与Fredd [22] 等实验得到的结果相同。当将酸液以较低速度注入岩心时,酸的扩散速度较大,酸液与岩石充分反应形成面溶蚀;当注入酸的速率较大时,酸的扩散速度较小于对流速度,酸还未来的及与岩石充分反应,便进入到了地层深处,从而导致均匀模式的形成。只有在最优注入速度下,此时酸的扩散速度与对流速度相当,会导致蚓孔模式的形成,此时的注入速度是最优注入速度。当注入速率处在最优和较小之间,可以观察到锥形溶蚀,而当注入速率在最优和较大之间时,便形成了分枝蚓孔。
从图1中(B)列可以看出,在注入速度过高或者过低时,裂缝的存在对蚓孔的传播影响不大。当注入速度处于两者之间时,蚓孔传播主要沿着裂缝的方向,使得流入基岩的酸液减少,在形成的溶蚀结构中裂缝成为蚓孔结构的一部分,形成蚓孔细,且分枝少。这是因为裂缝具有较高的渗透率,酸液在沟通裂缝后迅速向前传播,从而抑制了蚓孔分枝的形成。有无裂缝的岩心酸化形成的溶蚀模式相同,这是因为酸岩反应主要受酸在岩石中的扩散速度与流动速度的影响,扩散速度主要与温度等其他条件有关,流动速度受注入速度的影响。这与储层中是否存在天然裂缝无关。所以当储层中存在天然裂缝时,酸岩反应形成的溶蚀模式并没有改变。从图1列可以看出,在裂缝型碳酸盐储层中,酸液的流动规律一般是注入的酸先溶蚀部分带有较高渗透率的岩石,然后朝着渗流阻力较低的裂缝方向前进,当基岩与裂缝沟通后,沿着裂缝前进一直到达裂缝尖端,然后继续溶蚀岩石,如此反复直到达到岩心突破;而在无裂缝的储层中只溶蚀基岩。
6.1.2. 裂缝对突破体积的影响
无因次突破体积是指注入的酸液体积与基岩中孔隙体积之比。在图2中绘制了注入速度与无因次突破体积之间的关系曲线,从图2中可以看出,随着注入速度的增加,有无裂缝两种情况下,酸液的突破体积的消耗均呈现出先减少后增加的趋势,无论注入速度是大或小,带有裂缝的岩心消耗的酸液体积对应的曲线,都位于无裂缝岩心的下方,且均存在一个最低点。在形成蚓孔溶蚀模式时消耗的酸液体积对应着曲线的最低点,有无裂缝情况下对应的最优注入速度相同。说明在相同注入速度下,酸液在天然裂缝中传播比在基岩中较快,裂缝的存在虽然不能改变岩心酸化形成的溶蚀模式,但是可以减少酸液消耗体积,缩短反应时间。
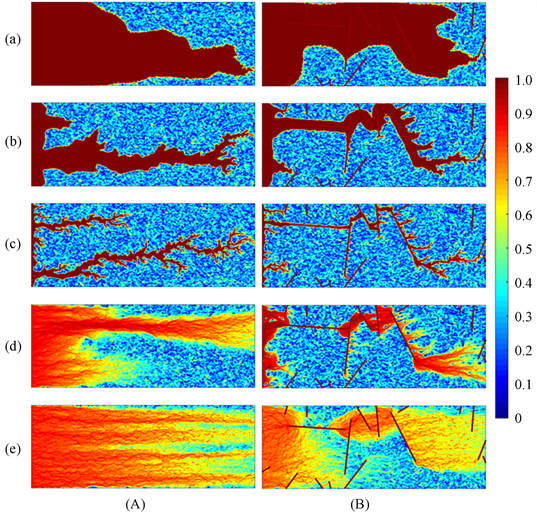
Figure 1. Comparison of dissolution patterns with and without natural fractures at different injection rates, (A) Dissolution patterns without fractures; (B) Dissolution patterns with fractures; the injection rates. (a) 1/Da = 9.8 × 10−7 (b) 1/Da = 9.80 × 10−6 (c) 1/Da = 9.80 × 10−5 (d) 1/Da = 7.84 × 10−3 (e) 1/Da = 0.15
图1. 不同注入速率有无天然裂缝情况下溶蚀模式的比较,(A) 不含裂缝的溶蚀模式;(B) 含裂缝的溶蚀模式;注入速度分别为:(a) 1/Da = 9.8 × 10−7 (b) 1/Da = 9.80 × 10−6 (c) 1/Da = 9.80 × 10−5 (d) 1/Da = 7.84 × 10−3 (e) 1/Da = 0.15
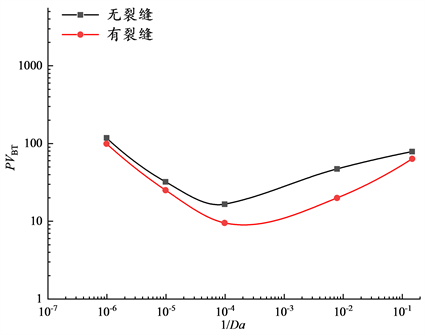
Figure 2. Influence of injection rate on dimensionless breakthrough volume
图2. 注入速度对无因次突破体积的影响
7. 结论
本文基于嵌入式离散裂缝模型建立了裂缝型碳酸盐岩反应流模型,通过对二维线性裂缝型碳酸盐岩反应流模型进行数值模拟,并分析了天然裂缝的存在对蚓孔扩展的影响,可以得到如下结论:
1) 天然裂缝存在不能改变酸蚀蚓孔的溶蚀模式。溶蚀模式的形成受注入速度和扩散速度的影响。当注入速度过高或者过低时,天然裂缝的存在对于蚓孔传播影响不大;当注入速度处于两者之间时,蚓孔传播主要沿着裂缝,形成的蚓孔结构细且分支少。
2) 天然裂缝的存在减少了酸液的消耗体积,在岩心达到突破时,无论是否含有裂缝的岩心消耗的酸液体积均呈现出先减少后增加的趋势,带有天然裂缝岩心消耗的PVBT均在不含天然裂缝的下方,且都有一个最低点,对应的最优注入速度相同。