多重折射率光子晶体谐振腔模型设计与仿真

Design and Simulation of Resonant Cavity Model for Multi Refractive Index Photonic Crystal

摘要: 本文提出了一种基于二维多重折射率光子晶体结构的谐振腔模型，这种谐振腔模型结构是由硅介质柱在空气背景中周期性排列而成。通过有限时域差分法、平面波展开法对光子晶体结构进行分析，发现该光子晶体结构中存在多种折射率。基于这种光子晶体进行谐振腔模型结构设计，利用快速傅里叶变换算法对该光子晶体谐振腔的折射率进行计算，验证出这种光子晶体谐振腔中存在两种折射率。随后研究了双重折射率光子晶体谐振腔模型中温度与谐振腔模型出射频谱波峰位置的关系，结果表明温度在0℃到240℃范围内每升高60℃，波峰位置向右定量移动0.014 μm。

Abstract: In this paper, a resonant cavity model based on a two-dimensional multiple refractive index pho-tonic crystal structure is proposed, which is composed of silicon dielectric columns arranged peri-odically in an air background. The photonic crystal structure is analyzed by finite time domain dif-ference method and plane wave expansion method, and it is found that there are multiple refractive indices in this photonic crystal structure. The resonant cavity model structure is designed based on this photonic crystal, and the refractive indices of the resonant cavity are calculated using the fast Fourier transform algorithm, and the existence of two refractive indices in the resonant cavity of this photonic crystal is verified. The relationship between the temperature and the wave peak posi-tion of the resonant cavity model in the dual refractive index photonic crystal resonant cavity is then investigated, and the results show that the wave peak position moves quantitatively to the right by 0.014 μm for every 60˚C increase in temperature in the range of 0˚C to 240˚C.

1. 引言

近年来，云计算与万物互联的概念逐渐得到广泛应用，他们背后的主要驱动力是数字化、网络化和智能化。同时对通信网络的传输及处理提出了更高的要求，但现阶段的通信传输仍以传统半导体材料构成集成电子通信器件。半导体材料是现代通信器材的核心组成部分，但随着技术的发展已经接近电子传输和能量转移的极限，无法满足通信器件高速化和集成化的需求。由于介电材料中光的传输速率和带宽远高于半导体中电子的传输速率和带宽，科学家们逐渐开始关注光子技术，希望通过光子而不是电子来传输、处理和存储信息 [1] [2] 。光子晶体 [3] [4] [5] (Photonic Crystal)的出现给光通信技术带来了新的生机和活力，通信网络中的器件逐渐被光子晶体器件取代，可以进一步增强信息的传输和处理能力 [6] [7] 。

光子晶体被称为“控制光子的半导体”，是由于根据其基本特性进行结构设计，可以达到调制光子的目的，它们被用于制造满足所需功能的集成器件，如光子晶体谐振腔。光子晶体谐振腔 [7] [8] 是一种利用光子晶体结构的能带特性来实现光场在空间中产生共振增强的器件，与传统的光学谐振腔相似，它们都是用来存储和增强光信号的装置。光子晶体谐振腔的原理是，由于光子晶体结构对特定波长具有高度选择性，因此只有符合条件(即满足布拉格衍射条件)的波长才能被存储在其中，在腔内来回运输同时发生振荡 [9] 。相比于传统微腔，光子晶体谐振腔的优点在于：制备工艺简单、易于集成、尺寸小巧、品质因数高等 [10] [11] 。因此，近年来光子晶体谐振腔被广泛应用于物理和工程领域，如非线性光学效应、量子信息处理、低阈值激光器、传感器以及滤波器等。2007年，池灏 [12] 等，提出了一种新型的双波长光子晶体谐振腔，总结了谐振腔的设计方法、关键参数和优化方法。受此启发，本文提出了一种基于双重折射率光子晶体以及光子晶体禁带理论的谐振腔模型。

2. 谐振腔模型建立与仿真

2.1. 模型准备

本文主要使用Rsoft软件的FullWAVE模块以及BandSOLVE模块进行建模仿真。其中FullWAVE模块：FullWAVE是一个全电磁场求解器，采用了时域有限元法(FEM)。它可以对复杂的三维光学结构进行建模和仿真，并且能够计算出其散射、透射、反射等参数。BandSOLVE：BandSOLVE是一个带隙结构求解器，可用于设计和优化布拉格反射镜、光子晶体等周期性结构。它采用了平面波展开(PWE)方法来计算这些结构中的色散关系和带隙宽度。

2.1.1. 双重折射率光子晶体的研究

在光子晶体中，介质柱的直径D又称为波导宽度，常被定义为 $D=b\cdot a$ ，其中b为任意小于1的值，a为光子晶体的晶格常数。本文提出了一种二维三角形结构的光子晶体，它是空气基底硅介质柱型的光子晶体，其中硅介质柱成六边形排列，介质柱的半径 $r=0.254\ast a$ ，介电常数 $\epsilon =11.5$ ，折射率 $n=3.42$ ，晶格常数 $a=618\text{nm}$ ，如图1所示。

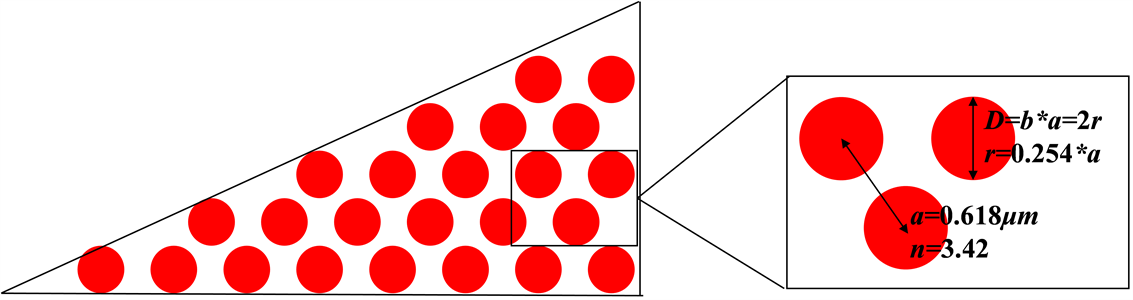
Figure 1. Schematic diagram of photonic crystal structure

图1. 光子晶体结构示意图

利用平面波展开法(PWM)分析上述结构TE模式情况下的能带情况，设定空气折射率为 $n_{空}=1$ ，硅介质柱折射率 $n_{硅}=3.42$ ，其它参数同上述结构。结果如图2所示，横坐标表示光子晶体倒格矢空间的三个坐标，纵坐标表示归一化频率，蓝色阴影部分表示光子晶体的带隙。从图中可以看到，该光子晶体具有三个禁带，频率落在禁带范围内的电磁波无法在光子晶体中传播。其中，第一带隙也就是图2中最下方的带隙对应归一化频率范围为0.245~0.369。

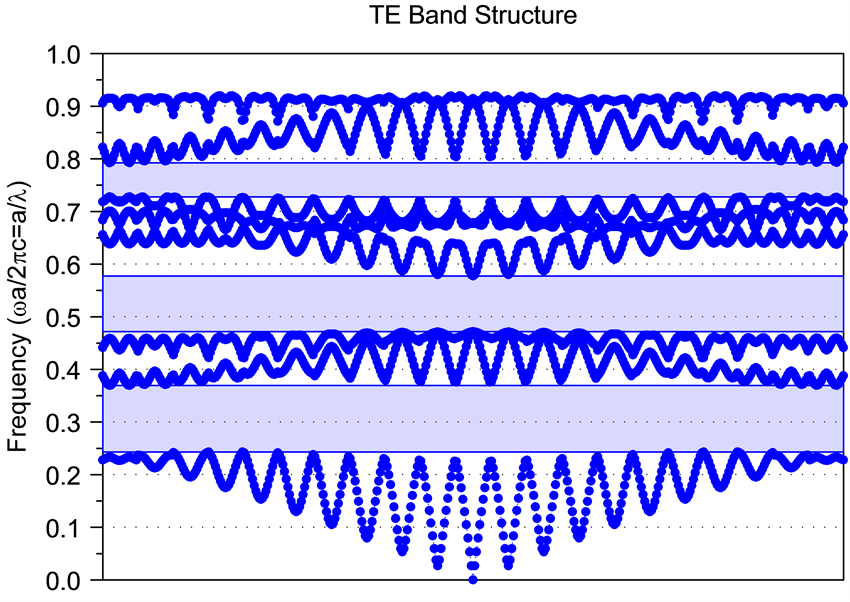
Figure 2. Photonic crystal energy band diagram of TE polarized light

图2. TE偏振光的光子晶体能带图

通过平面波展开法(PWM)计算出的光子晶体第一带隙的等频图如图3所示。等频图中心波矢k在各个方向模长为0，当波矢k逐渐增大时，图中等频线由内向外变化，归一化频率由0.4607减小到0.3704，表明在第一带隙范围内，群速度和相速度方向相反。同时，在TE偏振态下，坡印廷矢量和波矢k的点乘为负数，即光子晶体的等效折射率为负值。

Figure 3. Iso-frequency diagram of the first photonic band of a photonic crystal of TE polarized light

图3. TE偏振光的光子晶体第一光子带等频图

模拟采用波长 $\lambda =1.55\mu \text{m}$ 的光入射，其在等频图中对应等频线 ${\omega }_0=2\pi f$ 。在等频图中找到K_x与K_z的对应大小，可以得到对应波矢k的模大小为3.923。

根据归一化频率f与波数k的关系：

$k=\frac{\omega }{c}\cdot n_{eff}$ (2-1)

$f=\frac{\omega a}{2\pi c}=\frac{a}{\lambda }$ (2-2)

式中c表示真空中的光速， $\omega$ 表示角频率，由公式(2-1)和(2-2)可得光子晶体的等效折射率 $n_{eff}=k\lambda /2\pi \approx 0.968$ ，又因为是负折射率，所以应为等效负折射率约−0.968。

然后使用Rsoft软件的Fullwave模块，模拟频率 $f=0.369$ 的平行光源入射二维平行四边形光子晶体中的传播过程，如图4所示。从图中可以看出，平行光入射光子晶体后，在出射界面分为两束折射光，一束为符合折射定律的正折射光束a，另一束为违背折射定律的负折射光束b。

图4所示的模拟结果显示，这种结构的光子晶体中可能存在两种不同的折射率，为了验证这种现象的存在，我们采用数值计算的方式对光子晶体的折射率进行计算。首先基于时域有限差分法(Finite-Difference Time-Domain, FDTD)，对本文结构的光子晶体光传输数据进行处理。采用图1的双重折射率光子晶体参数，利用Rsoft软件的Fullwave模块对双重折射率光子晶体进行光场传输模拟，模拟过程如图5(a)所示。图5(a)表示平行光光源自左向右穿过光子晶体，我们对垂直光传输方向的振幅数据进行处理，得到振幅的电场周期性分布图，结果如图5(b)所示。

图5(b)为沿光传输方向的一维平均振幅电场分布图，其周期性比较复杂。为了得到不同折射率光束的频谱图，对图5(b)所示的电场分布做快速傅立叶变换(FFT)。得到光子晶体中不同折射率光束的频谱图如图5(c)所示。

从图5(c)中可以得到三种不同的频率，其中空气对应的频率为 $f_0$ ，负折射光束对应的频率为 $f_1$ ，正折射光束对应的频率为 $f_2$ 。根据公式 $n_i={\lambda }_i/{\lambda }_0=f_i/f_0$ ，其中， $f_0$ 为光在真空中的空间频率， $f_i$ 为各电场分量在光子晶体中的频率。计算出该结构的光子晶体折射率 $n_1=-1.245$ ， $n_2=2.079$ ，验证出双重折射率光子晶体同时具有两种折射率。

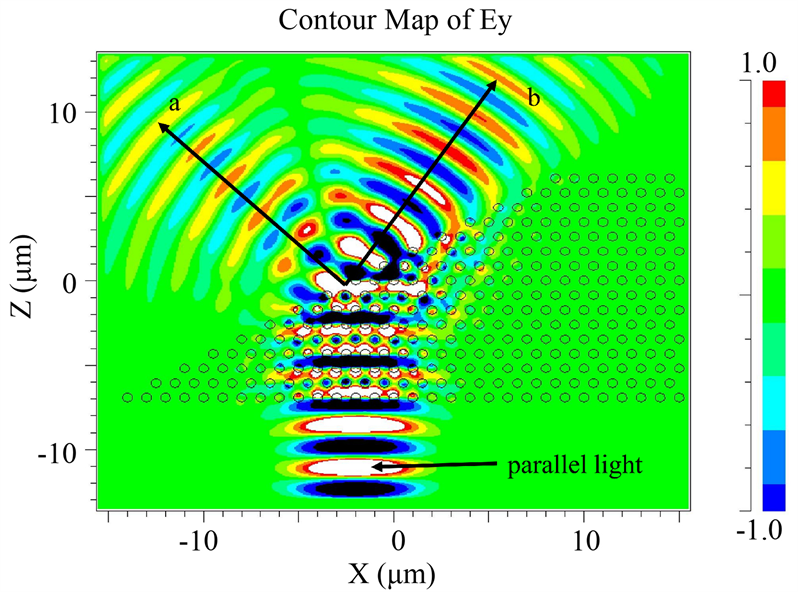
Figure 4. Propagation diagram of parallel light through a photonic crystal

图4. 平行光通过光子晶体的传播图

Figure 5. (a) optical path propagation diagram of the light beam transmitted in the photonic crystal; (b) periodic distribution of the optical field; (c) FFT spectrum of the electric field distribution along the transmission direction in the photonic crystal

图5. (a) 光束在光子晶体中传输的光路传播图；(b) 光场周期性分布图；(c) 光子晶体中沿传输方向的电场分布的FFT频谱图

由于双重折射率光子晶体中存在两种不同的折射率，那么由其构成的谐振腔中也可能存在不同的折射率，且这两种不同折射率的光束同时影响出射频谱的波峰位置。而采用平面波展开法只能计算一种折射率，无法解释光子晶体中的双重折射率现象，所以本文选择快速傅里叶变换法(FFT)分别计算双重折射率中的正折射率与负折射率。

2.1.2. 高反射率反射镜模型设计

本文尝试采用空气基底硅介质柱型二维光子晶体禁带结构来代谐振腔两侧的高反射率反射镜。其结构如图6所示，其中禁带介质柱层数为三层，空气折射率 $n_{空}=1$ ，硅介质柱折射率 $n_{硅}=3.45$ ，晶格常数 $a=0.618\mu \text{m}$ ，禁带的波导宽度定义为 $D_{禁}=m\cdot b\cdot a$ ，其中m表示直径倍率变量，用来控制介质柱直径大小。

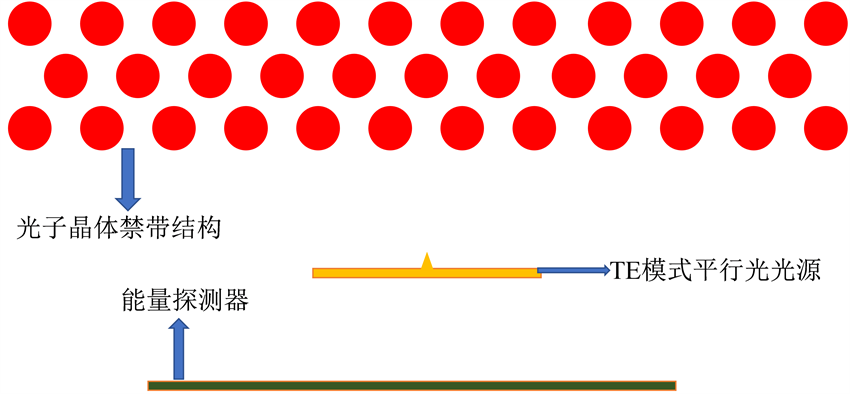
Figure 6. Schematic diagram of the forbidden band structure of a photonic crystal

图6. 光子晶体禁带结构示意图

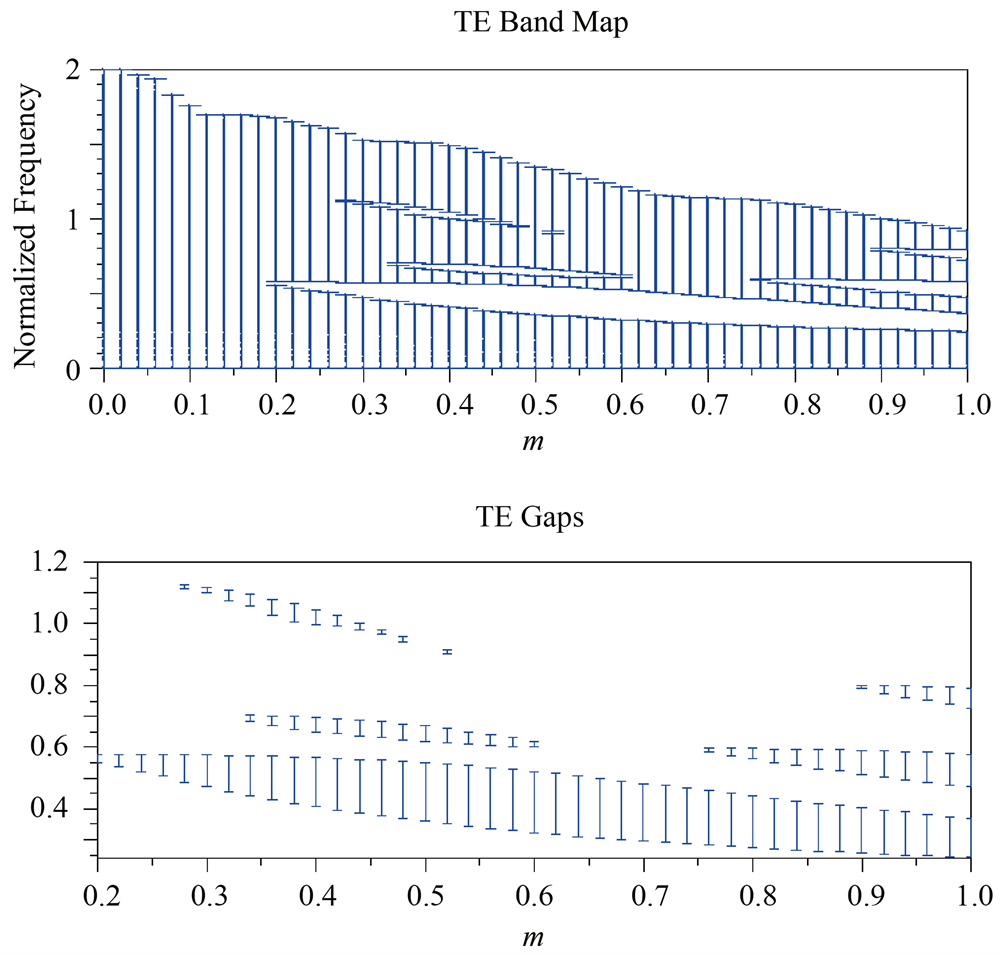
首先讨论光子晶体禁带介质柱大小与光子晶体禁带反射率的关系。利用Rsoft软件的BandSOLVE模块计算双重折射率光子晶体禁带与变量m的关系，如图7所示，TE Gaps表示光子晶体的禁带范围，随着变量m自0到1范围内不断增加，光子晶体的禁带在 $m=0.6$ 时光子晶体的带隙最宽，其对应归一化频率范围为0.335~0.586，即波长范围在1.07~1.86 μm。采用宽度为4 μm的平行光入射，经过光子晶体禁带反射后，通过探测器探测反射光能量，对不同直径宽度的硅介质柱禁带进行了反射率测量。

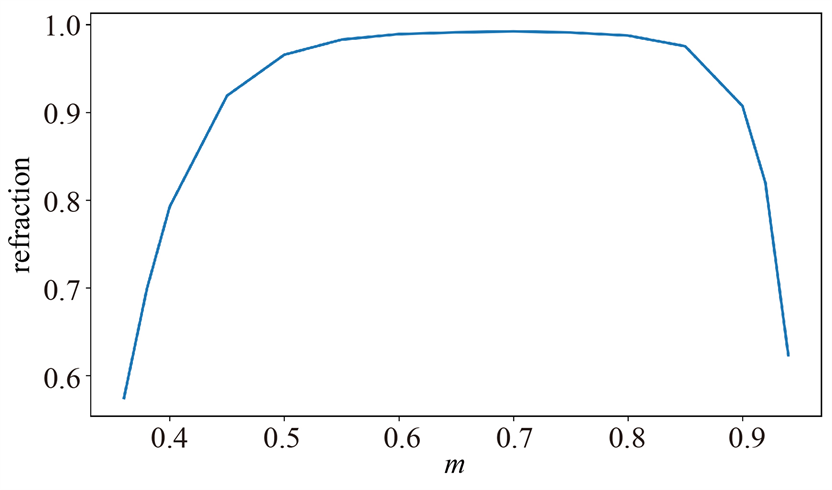(a)(b)

Figure 7. (a) plot of the variation of the forbidden band range for different diameter variables m; (b) plot of the reflectivity of the forbidden band for different diameter variables m

图7. (a) 不同直径变量m情况下的禁带范围变化图；(b) 禁带在不同直径变量m情况下的反射率图

测量结果如图7(b)所示，随着变量m的增加，光子晶体禁带的反射率先增加后减小，当硅介质柱直径变量m在0.463~0.892范围内时，光子晶体禁带的反射率高于90%，满足谐振腔高反射率反射镜的条件。

接着讨论光子晶体禁带层数与反射率之间的关系。考虑到入射光的波长大小以及谐振腔的腔长大小，选取光子晶体禁带层数变化范围为3~6层，结构参数同上文所述。利用Rsoft软件的Fullwave模块进行传播模拟，平行光光源发出光束打到光子晶体禁带上，通过探测器探测光子晶体禁带反射光束的能量，如图8所示。

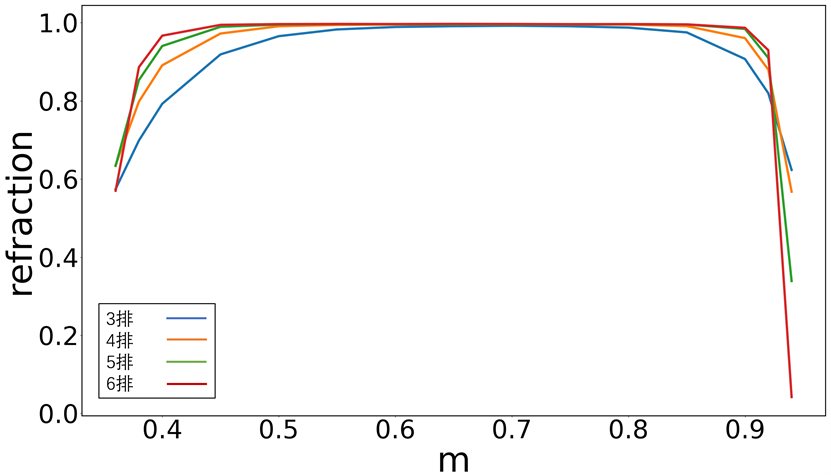
Figure 8. Reflectance curves of forbidden bands of photonic crystals with different number of rows

图8. 不同排数光子晶体禁带的反射率曲线

从图中可以看出，光子晶体禁带的层数在3~6层变化时，当介质柱系数m处于0.463~0.892范围内，均可达到高反射率反射镜的效果。考虑到谐振腔设计体积越小越佳，本文选取3层光子晶体禁带来代替传统光学谐振腔的高反射率反射镜。

2.2. 光子晶体谐振腔建模与仿真

替代高反射率反射镜的光子晶体禁带参数确定后，本文设计了一种由二维双重折射率光子晶体构成的谐振腔。如图9所示，谐振腔由上下两侧的光子晶体禁带，以及禁带中间部分的双重折射率光子晶体构成。其中谐振腔由六边形排列的硅介质柱构成，折射率为 $n_{硅}=3.45$ ，背景介质为空气，折射率 $n_{空}=1$ ，光子晶体晶格常数 $a=0.618\mu \text{m}$ ，入射通信波长范围为1.35~1.75 μm。双重折射率光子晶体的波导宽度定义为D_双 = b∙a，两侧禁带的波导宽度定义为 $D_{禁}=m\cdot b\cdot a$ ，其中m表示直径倍率变量，用来控制介质柱直径大小。

Figure 9. Schematic diagram of resonant cavity structure of double refractive index photonic crystal

图9. 双重折射率光子晶体谐振腔结构示意图

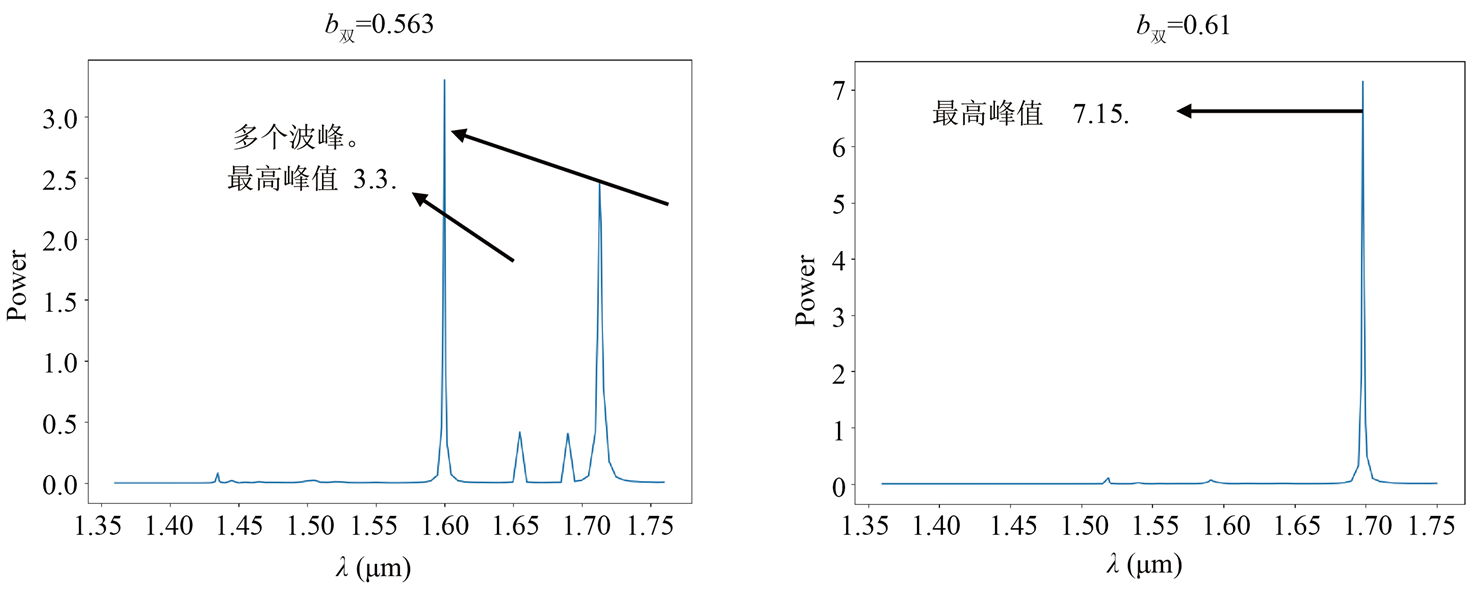
利用Rsoft软件的Fullwave模块进行模拟，分别测量双重折射率光子晶体参数b_双 = 0.563，b_双 = 0.61三种情况下的出射频谱。结果如图10所示，b_双 = 0.563的情况下，出射频谱存在2个峰值相差不大的波峰，峰值能量分别为3.3和2.45；b_双 = 0.61的情况下，出射频谱仅存在一个最高峰，峰值能量为7.15。

(a) (b)

Figure 10. Emission spectrum of a double refractive index photonic crystal resonant cavity for different b_双 cases

图10. 双重折射率光子晶体谐振腔不同b_双情况下的出射频谱图

从图10所示的出射频谱可以看出，双重折射率光子晶体谐振腔实现了光学谐振腔特定频率光放大的功能。且b_双 = 0.563情况下，双重折射率光子晶体谐振腔的出射频谱波峰数量大于一个，与预期单一波峰出射频谱不符。模拟结果表明，基于双重折射率光子晶体的谐振腔模型的出射频谱可以突破单一波峰的限制。

2.3. 谐振腔模型应用

由于谐振腔结构采用硅为介质柱材料，当温度发生变化时，硅的折射率也会随之发生改变，因而导致整个光子晶体的折射率发生改变。在光子晶体工作温度范围内，介质折射率变化与温度的变化间的关系可表达为

$\Delta n=\alpha n_0\Delta T$ (2-3)

而介质折射率的表达式为

$n=n_0+\Delta n$ (2-4)

结合公式(2-3)和公式(2-4)

$n=n_0+\alpha n_0\Delta T$ (2-5)

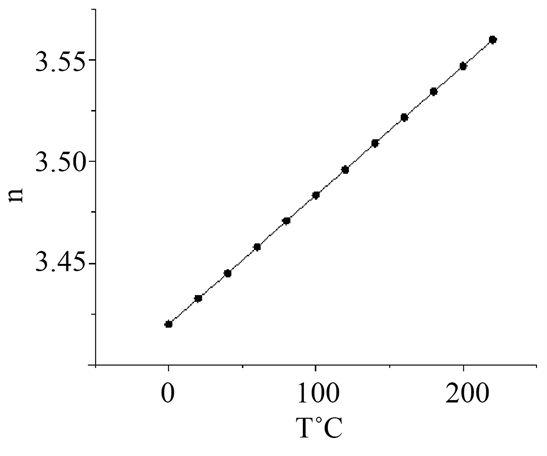
其中 $n_0$ 为介质的折射率，此结构中硅的折射率 $n_0=3.42$ ， $\alpha$ 为介质的热光系数，硅的热光系数为 $\alpha =1.86\times {10}^{-4}/˚\text{C}$ 。∆T为工作中的温度变化量。硅介质折射率随工作温度变化(0~220℃)关系如图11(a)所示，随着温度增高，硅的折射率不断增大。选取图9所示的双重折射率光子晶体谐振腔，b_双设定为0.518，在0℃到180℃范围内，分别探测谐振腔不同温度情况下的出射频谱。其中0℃、60℃、120℃的频谱结

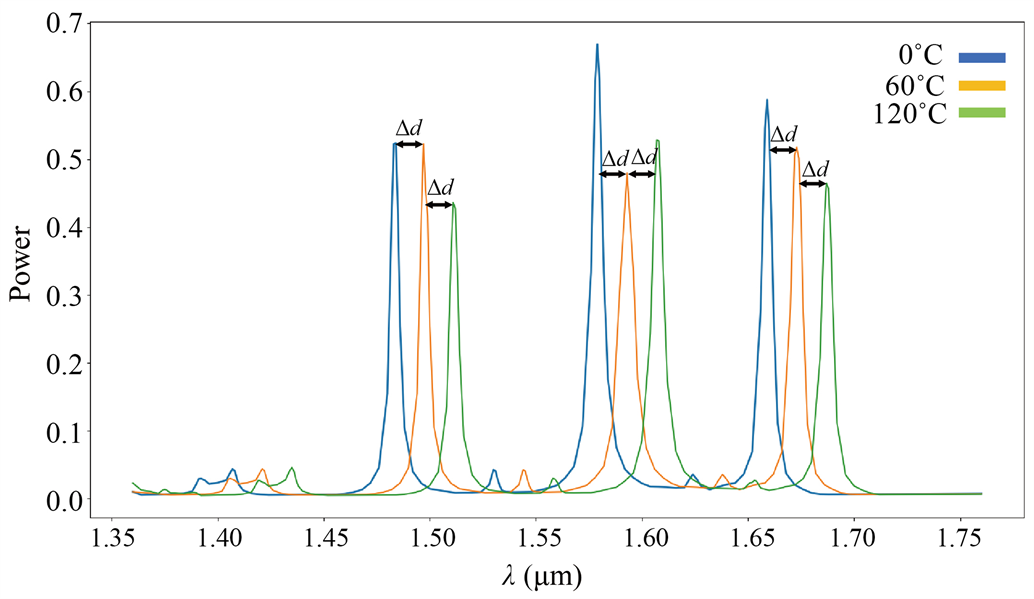(a) (b)

Figure 11. (a) Variation of refractive index of silicon dielectric with temperature; (b) Resonant cavity emission spectrum of dual refractive index photonic crystal at different temperatures

图11. (a) 硅介质折射率随温度变化关系；(b) 不同温度情况下双重折射率光子晶体谐振腔出射频谱图

果如图11(b)所示，从图中可以看出，随着入射波长的增加，出射频谱中存在3个波峰，同时温度每增加60℃，所有波峰位置向右移动定量距离 $\Delta d=0.014\mu \text{m}$ 。这种频谱随温度定量移动的关系，在温度传感器以及探测器方面具有参考价值。

3. 结论

本文基于光子晶体禁带以及光子晶体的双重折射率效应，设计了一种以空气为基底的硅介质柱双重折射率光子晶体谐振腔。该谐振腔与传统的谐振腔不同之处在于，采用平面波展开法(PWM)计算过的光子晶体禁带来替代光学谐振腔两侧的高反射率反射镜，加工方便且节省成本；在谐振腔中使用双重折射率光子晶体材料，通过傅里叶快速变换(FFT)计算的方法，验证了这种谐振腔的出射频谱可以突破单一波峰的限制；同时研究了双重折射率光子晶体谐振腔模型中温度与谐振腔模型出射频谱波峰位置的关系，结果表明温度在0℃到240℃范围内每升高60℃，波峰位置向右定量移动0.014 μm。