1. 引言
定时器是一种用于定时测量时间或控制事件序列的电子电路装置。定时器的工作原理可以概括为:将电容器充电至设定电压,当电容器电压达到设定电压时,输出一个脉冲信号。定时器是按配置的自激震荡周期乘以计数次数为计时时长的,但由于定时器震荡模块的震荡周期与配置的电阻与电容值为非线性关系,即便是美国安森美半导体(ON Semiconductor)的定时器系列产品,其使用手册中也没有提供较为方便的阻容计算方案,所以工程中通常需要进行多次试验以确定选配的阻容参数。为解决上述问题,本文设计了一种基于LabVIEW的自动标定系统,不仅能够直接计算出较为精准的阻容值,相关标定试验还实现了数据的自动采集及处理,一方面相比常用的人工逐个测试提高了效率,减少了标定试验所花时间,同时避免了人工测试可能带来的误差 [1] ;另一方面对表格内数据进行二维回归分析,得到电容电阻值与自激震荡周期的二维回归方程,方便后续对自激震荡周期的精确计算。
2. 标定系统原理结构
设计了一种定时器震荡周期标定系统,由小到大调节电位器的阻值,通过LabVIEW程序实时检测电表测量结果,当测量的阻值达到程序设定的阈值时,采集示波器的测出的震荡周期以及电表测出的电阻电容值,并分别填入LabVIEW对应的数据表格,完成后续数据处理所需的定时器相关参数测量。
接着在LabVIEW内进行数据处理。想要将定时器震荡模块的周期T与配置的电阻值R和电容值C之间的关系以关系式的形式表示。由于定时器的震荡模块为蓄积翻转型自激震荡电路,其时间常数与配置的电阻值、电容值均有关,因此在分析震荡周期T时,需要同时考虑配置的电阻值与电容值。于是,本文采用二元回归分析来对上述问题进行求解分析,二维回归分析原理如图1。二维回归分析法基本原理为:由二维回归方程来建立被测目标参量与输入参数之间的对应关系。然后,按最小二乘法原理由实验标定数据计算出均方误差最小条件下回归方程中的系数。这样,测量时测得了电阻与电容的两个值,就可由己知系数的二维回归方程来计算出相应的输入被测目标参数 [2] 。
由于震荡周期与配置的电阻电容值都是可以测量的,所以过程的动态特性必然表现在这些测量数据之中,那么就可以利用采集数据所提供的信息来建立过程的数学模型。
3. 标定系统数据处理程序设计
3.1. 算法描述
因为震荡周期T不是电阻值R的一元函数。现在同时测量电容值C,则震荡周期T可以用R及C二元函数来表示更合适,即
(1)

Figure 1. Schematic diagram of two-dimensional regression analysis
图1. 二维回归分析原理框图
由二维坐标(C, R)确定的T在同一曲面上,可通过曲面拟合,即二维回归方程表述
(2)
式中,T为回归分析修正后的震荡周期,R为测得的电阻值,C为测得的电容值,
为常系数;
为高阶无穷小。求解出式(2)中的所有常系数,则配置的电阻电容值和震荡周期T的二元输入——输出特性,即二维回归方程式(2)就确定了。当选定了电容值C以及电阻值R后,代入式(2)中就可以计算得到震荡周期
经过回归分析修正后的震荡周期T。所以,需先对定时器震荡模块二维标定试验,再对LabVIEW采集记录在数组中的数据进行计算,按最小二乘法原理确定常系数
[3] 。
3.2. 标定实验
在定时器工作范围内,确定m个电容值标定点,n个电阻值标定点,于是在各个标定点的标准输入值为:
对应于这些选定的标定点
和R,标定实验在n种不等电阻值下对定时器震荡模块做静态标定,采集得到对应m条配置了不同电容值的输入——输出特性,即
特性簇如图2所示。
3.3. 二次曲面拟合方程待定常数的确定
为了确定式(2)所表征的二次曲面拟合方程中的常系数,通常根据最小二乘原理,求得的系数值应满足均方误差的最小条件。
由二维回归分析法计算得到的
与实验标定值
之间存在误差e,其方差为:
(3)
式中:
。
若使
与标定值
拟合最好,根据最小二乘原理,其均方误差R应最小:
(4)
由式(4)可见,均方误差R是
的函数。我们可根据输入输出数据,极小化R,求参数
。使得R最小,然后把求得的参数
代入到(2)就可以确定二次曲面方程,从而求得经过二元回归分析的震荡周期T。根据多元函数求极值条件,令各偏导数为0,即:
(5)
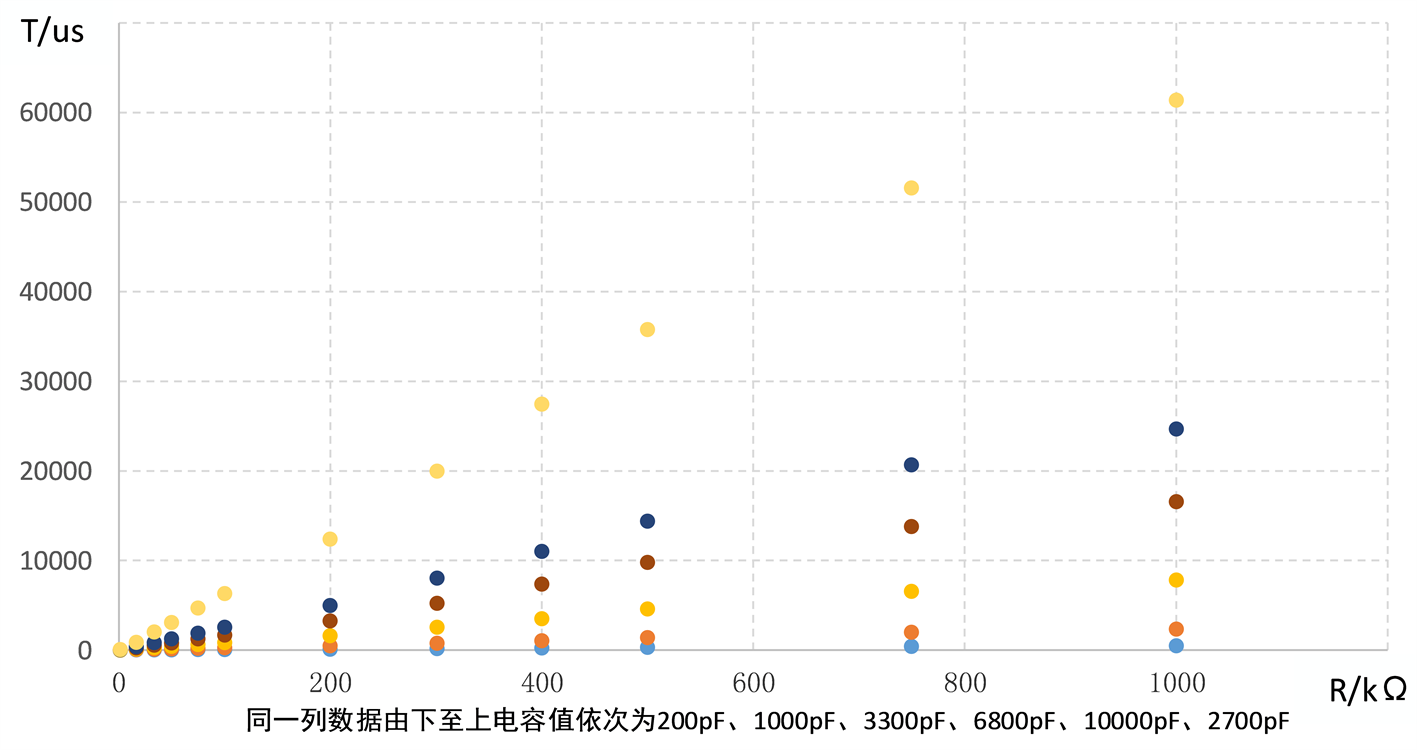
Figure 2. Timer oscillation module
characteristic cluster
图2. 定时器震荡模块
特性簇
整理可得如下六个方程:
(6)
方程组中:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
根据实验选配的电阻电容值,定时器震荡模块周期
和电表测试值
、
;可联立求解方程组(6),于是常系数
得以确定。
至此,二维曲面拟合方程(2)就完全确定了
。在实际运用中,把选配好的电容值和需求的定时器震荡周期T分别代入已经确定的拟合方程所算出来的值也就是经过拟合后的电阻值。
4. 阻容值对振荡周期的影响
从拟合曲面可以看出当震荡周期处于一定范围内且阻容值合适时,振荡周期与阻容值乘积的商趋于稳定。为进一步探索阻容值乘积与震荡周期的关系,选取了12个点阻值、6个电容值进行计算,列出振荡周期与阻容值乘积的商的对比表格,如表1所示,研究其变化趋势。

Table 1. The quotient of the product of oscillation period and resistance capacitance value
表1. 振荡周期与阻容值乘积的商
由表1可知,当震荡周期大于100 us,即震荡频率小于10 kHz情况下,振荡周期与阻容值乘积的商范围较窄,基本都在2~3之间。当电阻值小于50 kΩ时,振荡周期与阻容值乘积的商会随着阻值变小而增加,当电容值达到27 nF时,振荡周期与阻容值乘积的商则会开始减小。
5. 结论
设计了一种定时器震荡周期标定系统,并说明了二维回归分析算法的推导过程。将定时器相关引脚连接示波器、电表和计算机,实现了对定时器震荡电路的自动标定,极大减少了测试所需时间,提高了测试效率;通过LabVIEW进行自动标定,实现了数据自动采集和数据处理。搭建的标定测试台通过简单调整可用于国内外多种定时器电路的测试。标定系统的精度和采集的数据量与所选阻容值有关,根据不同的需求调整软件程序即可。除此之外,还根据振荡周期与阻容值乘积的商分析了阻容值对频率的影响,进一步证明了定时模块振荡周期的非线性,采用软件计算对提高震荡频率精确度很有意义。