具有无症状感染者的SEIAC模型动力学研究

Dynamics Study of a SEIAC Model with Asymptomatic Patient

摘要: 本文基于无症状感染者在疾病传播过程中的作用，建立了一类具有无症状感染者的SEIAC动力学模型，利用下一代矩阵得到决定疾病存在与否的基本再生数R0，通过构造Lyapunov函数得到当R0 < 1时，无病平衡点是全局渐近稳定的，即疾病最终趋于灭绝；而当R0 > 1时，地方病平衡点是全局渐近稳定的，即疾病将持续存在成为地方病。最后借助Mathematica软件对基本再生数进行敏感性分析及模型数值模拟。结果表明：提高治疗水平有利于疾病的防控，忽视无症状感染者的影响将低估疾病的传播情况。该结果将为具有无症状感染者的传染病的防控提供一定的理论支撑。

Abstract: Based on the role of asymptomatic patient in the process of disease transmission, this paper estab-lishes a SEIAC dynamic model with asymptomatic patient. The next generation matrix is used to obtain the basic reproduction number R0 that determines the existence of the disease. By con-structing the Lyapunov function, it is obtained that when R0 < 1, the disease-free equilibrium is globally asymptotically stable, that is, the disease eventually tends to extinction, when R0 > 1, the endemic equilibrium is globally asymptotically stable, in other words, the disease will persist and become endemic. Finally, the sensitivity analysis and model numerical simulation of the basic re-production number are carried out by Mathematica. The results show that improving the treatment level is conducive to the prevention and control of the disease, and ignoring the impact of asymp-tomatic patient will underestimate the spread of the disease. The results will provide some theo-retical support for the prevention and control of infectious diseases with asymptomatic patient.

1. 引言

传染病是指由病原微生物和寄生虫感染人体后产生的有传染性、在一定条件下可能流行的疾病，它可以在动物与动物、人与人或人与动物之间相互传播。其流行离不开三大要素：传染源、传播途径和易感人群。因此在制定防控措施时，主要是基于这三个要素展开。传染病动力学模型是预测传染病发展趋势、评估防控措施有效性的有力工具之一。传染病的传播动力学模型建模方式主要包括四种：仓室模型、多种群模型、基于个体的模型和网络模型。1927年Kermack与McKendrick [1] 提出的SIR仓室模型为其发展奠定了坚实基础，随后传染病动力学得到蓬勃发展。如今，传染病动力学模型越来越符合实际，如杨赟和赵亚男 [2] 考虑了疫苗接种的影响，张志琪 [3] 利用随机传染病模型探讨了环境中噪音干扰对COVID-19的传播的影响，何丹等 [4] 分析了广州市艾滋病流行趋势等。

无症状感染者是指易感者在感染过程中隐性感染，即病原体在入侵人体后，仅仅诱发机体产生特异性免疫应答，而不引起或只引起轻微的组织损伤，在临床上不显示出任何症状和体征，只能通过免疫学检查才能被发现。研究发现大部分传染病都存在无症状感染，如COVID-19 [3] 、SARS [5] 、口蹄疫 [6] 、埃博拉出血热 [7] 等。借助传染病动力学模型无疑有助于人们理解无症状感染者对疾病传播的影响，如Bellan等 [8] 通过建立并分析有无症状感染的埃博拉模型分析无症状感染者对埃博拉疫苗接种的影响，结果表明，忽视无症状感染致使有症状感染的累计发病率和人口接种疫苗覆盖率都可能会被高估。再如，Gao等 [9] 分析了人口移动情况下，无症状感染者在疾病传播中的作用。

本文将重点分析具有无症状感染者的传染病动力学模型，通过理论分析和数值模拟探讨无症状感染者对疾病传播的影响。具体安排如下：第二节将根据无症状感染者的传播机理建立模型；第三节将计算模型的基本再生数及平衡点；然后再下一节探讨平衡点的局部和全局稳定性；之后，借助软件对基本再生数进行敏感性分析和数值模拟，最后给出本文总结。

2. 建立模型

依据无症状感染者的传播机理，本文中将人口分为易感者S，潜伏者类E，无症状感染者类A，有症状感染者类I和确诊患者C。基于疾病流程图1，建立如下的动力学模型：

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\Lambda -\beta SI-\sigma \beta SA-dS,\\ \frac{\text{d}E}{\text{d}t}=\beta SI+\sigma \beta SA-\left({\delta }_A+{\delta }_I+d\right)E,\\ \frac{\text{d}A}{\text{d}t}={\delta }_{A}E-\left(\theta +\mu +d\right)A,\\ \frac{\text{d}I}{\text{d}t}={\delta }_{I}E+\theta A-\left(\omega +d\right)I,\\ \frac{\text{d}C}{\text{d}t}=\mu A+\omega I-\left(\gamma +d\right)C,\end{array}$ (1)

其中，参数 $\beta$ 表示有症状感染者感染的概率，参数 $\sigma$ 、 $\theta$ 表示无症状感染者相对于有症状感染者的感染率、转化率，参数d表示各类人群的死亡率。参数 ${\delta }_A$ 、 ${\delta }_I$ 分别表示潜伏者转为无症状感染者和有症状感染者的比率，参数 $\mu$ 、 $\omega$ 分别表示无症状、有症状患者的确诊率，参数 $\gamma$ 表示确诊患者的恢复比率。假设系统(1)满足如下初始条件

$S\left(0\right)\ge 0$ , $E\left(0\right)\ge 0$ , $A\left(0\right)\ge 0$ , $I\left(0\right)\ge 0$ , $C\left(0\right)\ge 0$ .

Figure 1. Model flow chart

图1. 模型流程图

3. 平衡点和基本再生数

令模型(1)中方程的右端全为零，即

$\{\begin{array}{l}\Lambda -\beta SI-\sigma \beta SA-dS=0,\\ \beta SI+\sigma \beta SA-\left({\delta }_A+{\delta }_I+d\right)E=0,\\ {\delta }_{A}E-\left(\theta +\mu +d\right)A=0,\\ {\delta }_{I}E+\theta A-\left(\omega +d\right)I=0,\\ \mu A+\omega I-\left(\gamma +d\right)C=0\text{,}\end{array}$ (2)

当 $I=0$ 时，可得系统(1)存在一个无病平衡点 $P_0=\left(\frac{\Lambda }{d},0,0,0,0\right)$ 。定义 $S_0=\frac{\Lambda }{d}$ 。根据Dreessche和

Watmough [10] 提出的下一代矩阵方法，在无病平衡点处新增感染率F和个体从仓室中转出矩阵V分别为：

$F=\left(\begin{array}{ccc}0& \sigma \beta S_0& \beta S_0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$ , $V=\left(\begin{array}{ccc}{\delta }_A+{\delta }_I+d& 0& 0\\ -{\delta }_A& \theta +\mu +d& 0\\ {{\displaystyle -\delta }}_I& -\theta & \omega +d\end{array}\right)$ ,

对转出矩阵V求逆矩阵可得：

${{\displaystyle V}}^{-1}=\left(\begin{array}{ccc}\frac{1}{{\delta }_A+{\delta }_I+d}& 0& 0\\ \frac{{\delta }_A}{\left({\delta }_A+{\delta }_I+d\right)\left(\theta +\mu +d\right)}& \frac{1}{\theta +\mu +d}& 0\\ \frac{{\delta }_I\left(\theta +\mu +d\right)+{\delta }_A\theta }{\left({\delta }_A+{\delta }_I+d\right)\left(\theta +\mu +d\right)\left(\omega +d\right)}& \frac{\theta }{\left(\theta +\mu +d\right)\left(\omega +d\right)}& \frac{1}{\omega +d}\end{array}\right)$ ,

系统(1)的下一代矩阵如下所示：

$F{V}^{-1}=\left(\begin{array}{ccc}\frac{{\delta }_A\left(\sigma \omega +\sigma d+\theta \right)+{\delta }_I\left(\mu +\theta +d\right)}{\left({\delta }_A+{\delta }_I+d\right)\left(\mu +\theta +d\right)\left(\omega +d\right)}\beta S_0& \frac{\beta S_0\left(\sigma \omega +\sigma d+\theta \right)}{\left(\mu +\theta +d\right)\left(\omega +d\right)}& \frac{\beta S_0}{\omega +d}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$ ,

计算可得 $F{V}^{-1}$ 矩阵的特征方程为：

$\left|\lambda I-F{V}^{-1}\right|=\left|\begin{array}{ccc}\lambda -\frac{{\delta }_A\left(\sigma \omega +\sigma d+\theta \right)+{\delta }_I\left(\mu +\theta +d\right)}{\left({\delta }_A+{\delta }_I+d\right)\left(\mu +\theta +d\right)\left(\omega +d\right)}\beta S_0& \frac{\beta S_0\left(\sigma \omega +\sigma d+\theta \right)}{\left(\mu +\theta +d\right)\left(\omega +d\right)}& \frac{\beta S_0}{\omega +d}\\ 0& \lambda & 0\\ 0& 0& \lambda \end{array}\right|=0$ ,

解得

${\lambda }_1=\frac{{\delta }_A\left(\sigma \omega +\sigma d+\theta \right)+{\delta }_I\left(\mu +\theta +d\right)}{\left({\delta }_A+{\delta }_I+d\right)\left(\mu +\theta +d\right)(\omega +d)}\beta S_0$ , ${\lambda }_2={\lambda }_3=0$ ,

其中最大的特征值为 ${\lambda }_1$ ，即模型的基本再生数为

$R_0=\frac{{\delta }_A\left(\sigma \omega +\sigma d+\theta \right)+{\delta }_I\left(\mu +\theta +d\right)}{\left({\delta }_A+{\delta }_I+d\right)\left(\mu +\theta +d\right)\left(\omega +d\right)}\beta S_0$ .

事实上，基本再生数R₀是一个非常重要的概念，它表示在发病初期，当所有人均为易感者时，一个感染者在其平均感染周期内所能感染的人数。

另外，当 $I\ne 0$ 时，计算方程组(2)可得，模型存在唯一的地方病平衡点 $P_1=\left(S^{*},E^{*},A^{*},I^{*},C^{*}\right)$ ，其中，

$S^{*}=\frac{\left({\delta }_A+{\delta }_I+d\right)\left(\mu +\theta +d\right)\left(\omega +d\right)}{\left[{\delta }_A\left(\sigma \omega +\sigma d+\theta \right)+{\delta }_I\left(\mu +\theta +d\right)\right]\beta }$ , $E^{*}=\frac{\left(\theta +\mu +d\right)\left(\omega +d\right)}{\theta {\delta }_A+{\delta }_I\left(\theta +\mu +d\right)}{I}^{*}$ ,

$C^{*}=\frac{{\delta }_A\left(\omega \theta +\mu d+\mu \omega \right)+{\delta }_I\omega \left(\theta +\mu +d\right)}{\left(\gamma +d\right)\left[\theta {\delta }_A+{\delta }_I\left(\theta +\mu +d\right)\right]}{I}^{*}$ , $A^{*}=\frac{{\delta }_A\left(\omega +d\right)}{\theta {\delta }_A+{\delta }_I\left(\theta +\mu +d\right)}{I}^{*}$ ,

$I^{*}=\frac{\theta {\delta }_A+{\delta }_I\left(\mu +\theta +d\right)}{\left[{\delta }_A\left(\sigma \omega +\sigma d+\theta \right)+{\delta }_I\left(\mu +\theta +d\right)\right]\beta }d\left(R_0-1\right)$ ,

4. 平衡点的稳定性

4.1. 无病平衡点P₀的稳定性

定理4.1若R₀ < 1，则系统(1)的无病平衡点P₀是全局渐近稳定的。

证明 构造合理的Lyapunov函数，

$U=E+\frac{\beta S_0}{\omega +d}I+\frac{\sigma \left(\omega +d\right)+\theta }{\left(\omega +d\right)\left(\mu +\theta +d\right)}\beta S_{0}A$ ,

显然U是正定的。计算U在系统(1)下的解的全导数，则有

$\begin{array}{c}\frac{\text{d}U}{\text{d}t}=\beta SI+\sigma \beta SA-\left({\delta }_A+{\delta }_I+d\right)E+\frac{\beta S_0}{\omega +d}\left({\delta }_{I}E+\theta A-\left(\omega +d\right)I\right)\\ +\frac{\theta +\sigma \left(\omega +d\right)}{\left(\theta +\mu +d\right)\left(\omega +d\right)}\beta S_0\left({\delta }_{A}E-\left(\theta +\mu +d\right)A\right)\\ =\beta SI+\sigma \beta SA+\frac{\theta \beta S_{0}A}{\omega +d}+\frac{{\delta }_I\left(\theta +\mu +d\right)+{\delta }_A\left(\theta +\sigma \omega +\sigma d\right)}{\left(\theta +\mu +d\right)\left(\omega +d\right)}\beta S_{0}E\\ -\left({\delta }_A+{\delta }_I+d\right)E-\beta SI-\frac{\theta +\sigma \left(\omega +d\right)}{\omega +d}\beta SA\\ =E\left({\delta }_A+{\delta }_I+d\right)\left(R_0-1\right)+\left(\beta I+\sigma \beta A\right)\left(S-S_0\right).\end{array}$

故当得R₀ < 1时，有 $\frac{\text{d}U}{\text{d}t}\le 0$ ，且 $\frac{\text{d}U}{\text{d}t}=0$ 当且仅当 $S\left(t\right)=\frac{\Lambda }{d}$ ， $E\left(t\right)=A\left(t\right)=I\left(t\right)=C\left(t\right)=0$ ，即 $\left\{\left(S,E,A,I,C\right):\frac{\text{d}U}{\text{d}t}=0\right\}$ 的最大不变集为单点集 $\left\{P_0\right\}$ 。根据LaSalle不变集原理得出结论，系统(1)的无病

平衡点P₀是全局渐近稳定的。

4.2. 地方病平衡点P₁的稳定性

定理4.2若R₀ < 1，系统(1)的地方病平衡点P₁是全局渐近稳定的。

证明 为讨论地方病平衡点P₁的全局稳定性，构造新的Lyapunov函数。令

$V_X={{\displaystyle X}}^{*}g\left(\frac{X}{{{\displaystyle X}}^{\text{*}}}\right)$ ,

其中 $g\left(x\right)=x-1-\ln x$ ， $x>0$ 。

由系统(1)的第一个方程及 $\Lambda -\beta S^{*}{I}^{*}-\sigma \beta S^{*}{A}^{*}-d{S}^{*}=0$ ，计算可得 $V_S$ 沿系统(1)解的全导数为：

$\begin{array}{c}\frac{\text{d}{V}_S}{\text{d}t}=\left(1-\frac{S^{*}}{S}\right)\frac{\text{d}S}{\text{d}t}=\left(1-\frac{S^{*}}{S}\right)\left(\Lambda -\beta SI-\sigma \beta SA-dS\right)\\ =\left(1-\frac{{{\displaystyle S}}^{*}}{S}\right)\left(\Lambda -\beta SI-\sigma \beta SA-dS-\Lambda +\beta S^{*}{I}^{*}+\sigma \beta S^{*}{A}^{*}+d{S}^{*}\right)\\ =\beta S^{*}{I}^{*}\left(1-\frac{S^{*}}{S}\right)\left(1-\frac{SI}{S^{*}{I}^{*}}\right)+\sigma \beta S^{*}{A}^{*}\left(1-\frac{S^{*}}{S}\right)\left(1-\frac{SA}{S^{*}{A}^{*}}\right)+d{S}^{*}\left(1-\frac{S^{*}}{S}-\frac{S}{S^{*}}+1\right)\\ =\beta S^{*}{I}^{*}\left(g\left(\frac{I}{I^{*}}\right)-g\left(\frac{S^{*}}{S}\right)-g\left(\frac{SI}{S^{*}{I}^{*}}\right)\right)+\sigma \beta S^{*}{A}^{*}\left(g\left(\frac{A}{A^{*}}\right)-g\left(\frac{S^{*}}{S}\right)-g\left(\frac{SA}{S^{*}{A}^{*}}\right)\right)\\ -d{S}^{*}\left(g\left(\frac{S^{*}}{S}\right)+g\left(\frac{S}{S^{*}}\right)\right)\\ =\beta S^{*}{I}^{*}\left(g\left(\frac{I}{I^{*}}\right)-g\left(\frac{SI}{S^{*}{I}^{*}}\right)\right)+\sigma \beta S^{*}{A}^{*}\left(g\left(\frac{A}{A^{*}}\right)-g\left(\frac{SA}{S^{*}{A}^{*}}\right)\right)-\Lambda g\left(\frac{S^{*}}{S}\right)-d{S}^{*}g\left(\frac{S}{S^{*}}\right).\end{array}$

根据系统(1)的第二个方程及 $\beta S^{*}{I}^{*}+\sigma \beta S^{*}{A}^{*}-\left({\delta }_A+{\delta }_I+d\right)E^{*}=0$ ，类似可得 $V_E$ 沿系统(1)解的全导数为：

$\begin{array}{c}\frac{\text{d}{V}_E}{\text{d}t}=\beta S^{*}{I}^{*}\left(g\left(\frac{SI}{S^{*}{I}^{*}}\right)-g\left(\frac{SI{E}^{*}}{S^{*}{I}^{*}E}\right)\right)+\sigma \beta S^{*}{A}^{*}\left(g\left(\frac{SA}{S^{*}{A}^{*}}\right)-g\left(\frac{SA{E}^{*}}{S^{*}{A}^{*}E}\right)\right)\\ -\left({\delta }_A+{\delta }_I+d\right)E^{*}g\left(\frac{E}{E^{*}}\right),\end{array}$

同理可得

$\begin{array}{l}\frac{\text{d}{V}_A}{\text{d}t}={\delta }_A{E}^{*}\left(g\left(\frac{E}{E^{*}}\right)-g\left(\frac{E{A}^{*}}{E^{*}A}\right)\right)-\left(\theta +\mu +d\right)A^{*}g\left(\frac{A}{A^{*}}\right),\\ \frac{\text{d}{V}_I}{\text{d}t}={{\displaystyle \delta }}_I{E}^{*}\left(g\left(\frac{E}{E^{*}}\right)-g\left(\frac{E{I}^{*}}{E^{*}I}\right)\right)+\theta A^{*}\left(g\left(\frac{A}{A^{*}}\right)-g\left(\frac{A{I}^{*}}{A^{*}I}\right)\right)-\left(\omega +d\right)I^{*}g\left(\frac{I}{I^{*}}\right),\\ \frac{\text{d}{V}_C}{\text{d}t}=\mu A^{*}\left(g\left(\frac{A}{A^{*}}\right)-g\left(\frac{A{I}^{*}}{A^{*}I}\right)\right)+\omega I^{*}\left(g\left(\frac{I}{I^{*}}\right)-g\left(\frac{C^{*}I}{C{I}^{*}}\right)\right)-\left(\gamma +d\right)C^{*}g\left(\frac{C}{C^{*}}\right),\end{array}$

考虑到如下的Lyapunov函数

$V=V_S+V_E+V_A+V_I+V_C$ ，

利用上面 $V_X$ 沿系统(1)解的全导数及 ${\delta }_A{E}^{*}-\left(\theta +\mu +d\right)A^{*}=0$ ， ${\delta }_I{E}^{*}+\theta A^{*}-\left(\omega +d\right)I^{*}=0$ ， $\mu A^{*}+\omega I^{*}-\left(\gamma +d\right)C^{*}=0$ ，整理可得

$\begin{array}{c}\frac{\text{d}V}{\text{d}t}=\frac{\text{d}{V}_S}{\text{d}t}+\frac{\text{d}{V}_E}{\text{d}t}+\frac{\text{d}{V}_A}{\text{d}t}+\frac{\text{d}{V}_I}{\text{d}t}+\frac{\text{d}{V}_C}{\text{d}t}\\ =\left(\beta S^{*}-d\right)I^{*}g\left(\frac{I}{I^{*}}\right)+\left(\sigma \beta S^{*}-d\right)A^{*}g\left(\frac{A}{A^{*}}\right)-\Lambda g\left(\frac{S^{*}}{S}\right)-d{S}^{*}g\left(\frac{S}{S^{*}}\right)\\ -d{E}^{*}g\left(\frac{E}{E^{*}}\right)-\left(\gamma +d\right)C^{*}g\left(\frac{C}{C^{*}}\right)-{\delta }_A{E}^{*}g\left(\frac{A^{*}E}{A{E}^{*}}\right)-{\delta }_I{E}^{*}g\left(\frac{E{I}^{*}}{E^{*}I}\right)\\ -\mu A^{*}g\left(\frac{C^{*}A}{C{A}^{*}}\right)-\omega I^{*}g\left(\frac{C^{*}I}{C{I}^{*}}\right)-\theta I^{*}g\left(\frac{A{I}^{*}}{A^{*}I}\right)\\ -\beta S^{*}{I}^{*}g\left(\frac{SIE}{S^{*}{I}^{*}{E}^{*}}\right)-\sigma \beta S^{*}{A}^{*}g\left(\frac{SAE}{S^{*}{A}^{*}{E}^{*}}\right).\end{array}$

假设 $\sigma <1$ 且 $\beta S^{\text{*}}<d$ 。显然，当 $\frac{\text{d}V}{\text{d}t}\le 0$ ，且 $\frac{\text{d}V}{\text{d}t}=0$ 的充要条件是 $S=S^{*}$ ， $E=E^{*}$ ， $A=A^{*}$ ， $I=I^{*}$ ， $C=C^{*}$ ，故系统(1)在集合 $\left\{\left(S,E,A,I,C\right)|\frac{\text{d}V}{\text{d}t}=0\right\}$ 中的最大不变集为 $\left(S^{*},E^{*},A^{*},I^{*},C^{*}\right)$ 。又由于Lyapunov函数V在R上有下界0，且当 $\left(S^{*},E^{*},A^{*},I^{*},C^{*}\right)\to +\infty$ 时， $V\to +\infty$ 。由文献 [9] 中的推论2.3.2，可知 $\left(S^{*},E^{*},A^{*},I^{*},C^{*}\right)$ 是全局渐近稳定的。根据渐近自治系统理论 [11] 可知，当R₀ > 1时，模型(1)的地方病平

衡点P₁是全局渐近稳定的。

5. 敏感性分析和数值模拟

为了使数值拟合效果更好，模型中的大部分参数是基于实际情况假设和参考已有的文献。参数的取值范围如表1所示：

Table 1. The value and significance of parameters for model (1)

表1. 模型(1)参数的取值及意义

为了分析出无症状感染者对传染病流行与否的影响，本文采用偏序相关法(PRCC)对基本再生数进行敏感性分析，得到了不同参数对R₀的影响，如图2所示。结果表明，参数 $\mu$ 、 $\omega$ 与R₀强负相关，说明对疾病的治疗强度越大，基本再生数将越小，越有利于疾病的控制；值得一提的是，参数 $\sigma$ 与R₀强正相关，说明接触的易感者接触的无症状感染者越多，基本再生数将越大，流行程度将越强，即减少与无症状感染者的接触将有利于疾病的防控。

为进一步探讨无症状感染者对疾病的影响，本文对比模拟了不同类型感染者对传染病的流行趋势的影响，如图3所示。其中，有症状感染者表示感染者类型中仅存在有症状感染者，无症状感染者表示感染者类型中既存在有症状感染者又存在无症状感染者，且初始条件下感染者人数相同。结果表明，在没有外力干涉的情况下，当R₀ < 1时，若感染者中不存在无症状感染者，感染人数会持续急速下降。若感染者中存在无症状感染者，感染人数会在短期内增加，但一段时间后减少，疾病终将消亡。当R₀ > 1时，由图可得，若感染者中存在无症状感染者，感染人数总会比有症状感染者时多，且相对于仅有有症状感染者的情况，更早到达稳定点。这说明忽视无症状感染的确会加速传染病的流行，同时增加传染病的流行强度。

Figure 2. Sensitivity of basic reproduction number (R₀)

图2. 基本再生数R₀的敏感性

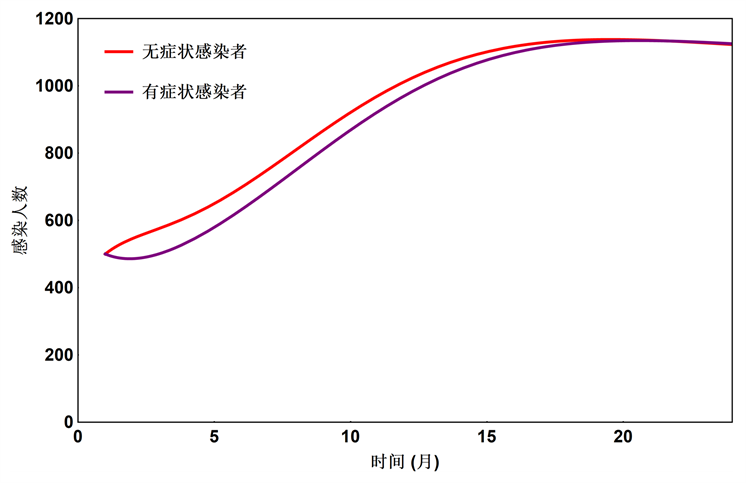
Figure 3. The number of infected population when R₀ = 0.2482 (Left) and R₀ = 3.132 (Right)

图3. R₀ = 0.2482 (左)和R₀ = 3.132 (右)情况下感染者人数变化

6. 总结

本文提出了一类具有无症状感染者的SEIAC模型，得到了模型的基本再生数R₀及模型的无病平衡点及地方病平衡点的具体表达式，理论分析结果表明：当R₀ < 1时，疾病不会流行，当R₀ > 1时，疾病流行，因此R₀ = 1是区分疾病能否流行的阈值。当R₀ < 1时，表示一个染病者在平均患病期内的感染人数小于1，无病平衡点全局渐近稳定，疾病逐渐自然消亡。当R₀ > 1时，表示一个染病者在平均患病期内的感染人数大于1，地方病平衡点全局渐近稳定，疾病将会流行。因此要防治疾病流行，必须使R₀ < 1。最后在假设条件下进行数值模拟。

基金项目

宁夏自然科学基金(2023AAC03089)。

NOTES

^*通讯作者。