高速空气静压电主轴止推轴承设计及性能分析

Design and Performance Analysis of the Static Air Pressure Thrust Bearing on the High Speed Electric Spindle

摘要: 高速空气静压电主轴具体有结构紧凑、高转速等特点被广泛应用于高精密机床、多关节机器人、汽车制造、医疗装备等高新技术领域设备中。空气止推轴承是高速空气静压电主轴实现高精度高转速的关键零部件。本文对单孔和多孔空气静压止推轴承建立数学模型，利用ANSYS Workbench Fluent软件进行详细的刚度、气膜压力、气体流场、承载能力模拟设计分析计算，分析轴承参数对轴承刚度的影响，得到轴承性能随各项参数变化的变化规律，实现该类轴承的参数设计。进一步，利用MATLAB app designer编制计算空气静压止推轴承的参数化设计界面软件，提供基于公式的MATLAB计算与基于有限元的ANSYS计算比较分析结果，明晰各设计参数下空气止推轴承的刚度以及承载能力等关键性能。

Abstract: High speed aerostatic electric spindles are widely used in high-tech fields such as high-precision machine tools, multi joint robots, automotive manufacturing, medical equipment, and other high-tech equipment as well as other compact and high-speed high-tech equipment. Air thrust bearing is a key component for achieving high precision and speed in high-speed air hydrostatic electric spindle. In this article, the mathematical models for single hole and porous air hydrostatic thrust bearings are established, and stiffness, gas film pressure, gas flow field, and bearing capacity are calculated with the ANSYS Workbench Fluent software and the MATLAB software. The influence of bearing parameters on bearing stiffness is analyzed, and the variation pattern of bearing perfor-mance with various parameters is obtained and compared to achieve parameter design of this type of bearing. Furthermore, the MATLAB app designer is used to compile the parametric design inter-face software for calculating aerostatic thrust bearings, and provides the comparative analysis re-sults of formula-based MATLAB calculations and finite element-based ANSYS calculations, so as to clarify the key properties such as stiffness and load carrying capacity of air thrust bearings under various design parameters.

1. 引言

随着高速加工技术的迅速发展和广泛应用，各工业部门特别是航天、航空、汽车和模具加工等行业对高转速、高精度、高效率和高可靠性的高速空气静压电主轴的需求越来越迫切 [1] 。空气用作轴承中的润滑剂，可实现低摩擦减阻和小间隙精密结构设计 [2] 。

空气静压轴承是高速空气电主轴中最重要的一部分，其性能是整个主轴的关键性能。Miettinen等人通过总结前人的研究给出了空气静压轴承性能的基本计算公式 [3] 。Hosokawa等人为了实现更高的轴承运动精度，设计具有多入口孔的空气静压轴承，分析了其静态特性 [4] 。薛龙等人建立了一套对多孔空气静压止推轴承进行分析的数学模型 [5] 。Miettinen等人使用线性动力学分析评估轴承的稳定性，提出了基于机械和机电一体化的解决方案 [6] 。田洋通过有限元方法分析完成了对单孔、多孔空气轴承的承载性能、流场特性等研究 [7] 。孙哲哲等人利用Fluent模拟仿真对止推气体轴承的承载能力和刚度进行分析 [8] 。

本文在前人的各项研究成果基础上，采用Miettinen [3] 总结的静压轴承性能的基本计算公式完成对空气电主轴以及气体润滑轴承的数学建模及MATLAB程序编程，采用ANSYS Fluent有限元分析软件对设计参数与对应性能进行仿真计算分析，MATLAB计算结果与ANSYS Fluent有限元分析结果对比，明确各气体轴承参数对于气体轴承性能的决定作用。

2. 空气止推轴承设计

为了使空气电主轴能适应更大的轴向力工作环境，一般采用两个相同的空气静压止推轴承，如图1所示，两个止推轴承均位于主轴的前端部分，分别布置在止推盘的两侧，在两止推轴承中间设置密封圈。前止推轴承一端与前端盖直接接触，前端盖处设计安装密封圈。后止推轴承一端与前径向轴承直接接触，其间无需设计密封。

止推轴承同样多气孔，并且设计为径向对称，保证气膜的刚度，提高轴向稳定性。设计采用若干节流孔的对称设计。节流孔型如图1所示，一般在进入节流孔前开设一环形均压槽，保证各节流孔进气压力相同，提高轴向精度。

Figure 1. Thrust bearing

图1. 止推轴承

3. 数学模型建立

3.1. 气膜厚度

在进行建模分析之前，首先应计算相应的空气静压止推轴承在其工作环境下所产生的气膜厚度，以后能得到精密的有限元分析结果。空气静压止推轴承工作时受力如右图所示。其中半径单位为mm，压力单位为pa，空气流动如箭头所示，气体经节流孔后，在径向方向上分别向内、向外流动，在半径为R1处排入大气，具体参数示意如图2所示。根据Navier-Stokes方程：

Figure 2. Parameter diagram

图2. 参数示意图

$\frac{{\partial }^{2}u}{\partial z^2}=\frac{1}{u}\frac{\partial p}{\partial r}$

$\frac{\partial p}{\partial z}=0$

$\frac{\partial p}{\partial \theta }=0$

其中：u为气流速度，m/s；p为任一处压力，Pa；r为任一半径处半径值。

将边界条件代入上式进行积分之后得到：

$\frac{\text{d}p}{\text{d}r}=-\frac{6\mu Q}{\pi r\rho h^3}$

其中：Q为流量，kg/s； $\rho$ 为空气密度，kg/m³。

再根据 $p=\rho RT$ 代入进行替换，根据目前所设边界条件可得出空气流动方程：

外向流动方程：

$p_a^2-p_d^2=-\frac{12\mu Q_{1}RT}{\pi h^3}\ln \left(r/R_0\right)$ (1)

其中：μ为空气动力粘度；R为气体常数，J/kg；T为绝对温度。

内向流动方程：

$p_a^2-p^2=\frac{12\mu Q_{1}RT}{\pi h^3}\ln \left(R_0/r\right)$ (2)

根据式(1) (2)可求得空气流动的质量流量：

外向流动流量：

$Q_1=\frac{\left(p_d^2-p_a^2\right)\pi h^3}{12\mu RT\ln \left(R_1/R_0\right)}$ (3)

内向流动流量：

$Q_2=\frac{\left(p_d^2-p^2\right)\pi h^3}{12\mu RT\ln \left(R_0/R_2\right)}$ (4)

又根据流入小孔的气体总流量有：

$Q_s=C_{D}A{P}_a\frac{1}{\sqrt{RT}}$ (5)

其中： $C_D$ 为流量系数，A为节流孔面积。

根据质量流量相等公式： $Q_s=Q_1+Q_2$ ，由公式(3) (4) (5)得到气膜的厚度：

$h={\left(\frac{12\mu C_{D}A{P}_a\sqrt{RT}}{\frac{p_d^2-p_a^2}{\ln \left(R_1/R_0\right)}+\frac{p_d^2-p^2}{\ln \left(R_0/R_2\right)}}\right)}^{1/3}$ (6)

3.2. 承载与刚度

该软件所计算结果包含设计的空气静压止推轴承的承载能力和刚度，根据前一章中的式(1) (2)可得压力情况：

$p=\{\begin{array}{c}\sqrt{p_d^2-\left(p_d^2-p_a^2\right)\frac{\ln \left(r/R_0\right)}{\ln \left(R_1/R_0\right)}}\\ R_1\ge r\ge R_0\\ \sqrt{p_d^2-\left(p_d^2-p^2\right)\frac{\ln \left(r/R_0\right)}{\ln \left(R_2/R_0\right)}}\\ R_0\ge r\ge R_2\end{array}$ (7)

对整个受力面进行积分，可求得承载能力：

$F=2\text{π}{\displaystyle {\int }_{R_2}^{R_0}pr\text{d}r}+2\pi {\displaystyle {\int }_{R_0}^{R_1}pr\text{d}r}+\text{π}{R}_2^{2}p-\text{π}{R}_1^2{p}_a$ (8)

由上公式可求导得刚度：

$K=\text{d}F/\text{d}h=\frac{\Delta F}{\Delta h}$ (9)

4. ANSYS分析

前部分中已经完成了对空气电主轴的整体设计，现对其主要零部件止推轴承进行详细的分析。

4.1. Fluent求解

利用mesh对模型进行网格划分，在对其进行网格划分时优先采用四边形网格而不是三角形网格，因为四边形网格的精度要高于三角形网格，要求其奇异点个数少，布局合理、面片的边走向与几何特征走向对齐、边长均匀化，或者自适应几何特征，并且因为气膜部分小但是相比之下为比较重要的部分，而管道部分只需计算刚度需求，要求普通。在划分网格时，气膜部分的网格因细而密且质量高，能精确计算气膜部分的要求，管道部分网格要求整齐满足条件即可，为减少计算步骤、提高计算效率，相应降低管道部分的网格质量。选用六面体主导网格法(Hex Dominant)得到四边形网格，在Size Function中选择使用Proximity控制该气孔模型中网格的增长率以及最大网格尺寸等控制网格精度差别，网格划分结果如图3所示。

Figure 3. Grid division

图3. 网格划分

网格划分结束之后，调整粘性参数(Viscous)，选用模型类型为k-epsilon (2 eqn)。设定流体为空气(air)，轴承材料选用铝。入口压力设置为0.6 Mpa，出口压力为0.1 Mpa。之后开始进行有限元分析运算。查看计算结果的云图和向量图可知，根据目前设定的边界条件，从压力图来看，如图4所示，整个轴承受力最大处为节流孔入口处，最大压力即为所设入口压力值，0.6 MPa，节流孔处压力均约为0.3 MPa，随后一直到出气口压力逐渐减小，因此在设计轴承选用材料时，仅需考虑工作环境压力保证材料强度足够即可。从图中能看出节流孔进口处并无压力损失，孔型设计合理。

Figure 4. Pressure calculation results

图4. 压力计算结果

如图5所示，从速度图像上来看，速度最大值集中在节流孔直径最小处(包含进出口两端)。从矢量标识显示，当前情况下虽重力在孔径向方向，但气体流动方向基本不受影响，符合对正常工作时轴承空气流动状态的基本假设。流速最大值出现在节流孔处，为850 m/s，速度较快，但出口速度值仅为42.6 m/s，远小于声速，不会产生激振现象，孔型设计合理。

Figure 5. Speed calculation results

图5. 速度计算结果

4.2. 节流孔个数对轴承性能的影响分析

对节流孔数为1~8的节流孔及其气膜模型进行建模，在同样的工作状态下，对节流孔个数进行改变，并且考虑到在工作时轴承动平衡与动不平衡的情况，将节流孔数均设计为偶数。如图6所示，节流孔个数的增加，大大改善了节流孔及气膜的受力情况。在只有一个节流孔时，气膜压力从1.24 × 10³ Pa到3.38 × 10⁴ Pa不等，受力不均匀，且压力值较大，当节流孔数增加到八个时，气膜边缘压力稳定在0.1 MPa左右，中间形成一圈压力为0.2 MPa的稳定压力环。同样的工作情况下，节流孔间的压力气膜随节流孔个数增加而增加，受力呈环状均匀分布，且节流孔附近的压力也随节流孔个数增加而增加，增大了轴承的承载能力。证明节流孔分布越密集，轴承的承载能力也越强，刚度越大，性能越高。

Figure 6. Analysis results of different number of holes

图6. 不同孔数分析结果

4.3. 气膜的影响

气膜是影响空气静压止推轴承性能的重要因素，现结合ANSYS分析结果，研究气膜厚度对性能的具体影响以及轴承参数对气膜厚度的影响。

在相同条件下，只改变气膜厚度，观察节流孔的受力以及孔中空气流动的变化。此时节流孔的参数为：出气口半径为R1 = 0.1 mm，进气口半径为R2 = 0.4 mm，斜面坡度为60˚。

经过有限元分析后结果如图7所示，图中(a)的气膜厚度为30 μm；(b)的气膜厚度为20 μm；(c)的气膜厚度为15 μm；(d)的气膜厚度为10 μm。看压力变化图，可以看出随着气膜厚度的减小，节流孔内压力铸件增大，气膜压力也随之增大。看速度变化图，可以看出随着气膜厚度的减小，节流孔内空气流动的最大速度值增大。并且出气口处的速度也在增大，在当前工作情况下，气膜厚度减小到时10 μm时出气口处的速度甚至超过了音速，达到了371 m/s。

由此可以得出，无论是从受力情况或是空气流速情况下考虑，在设计空气静压止推轴承时都应仔细考虑工作环境下所产生的气膜厚度，要保证有足够的气膜厚度。

Figure 7. Force and velocity under different air film thicknesses

图7. 不同气膜厚度时的受力与速度情况

5. Fluent仿真结果与MATLAB计算结果对比分析

将前述公式(8) (9)导入MATLAB中，利用公式计算出压力结果，与Fluent仿真结果进行对比分析。

5.1. 节流孔直径对轴承性能的影响

基本参数为轴承外径R1 = 17 mm；轴承内径R2 = 4 mm；节流孔分布半径R0 = 10 mm；出气口压强与工作压强均为0.1 MPa；节流孔数为8个；分别在进气口压强为0.5 MPa，0.6 MPa，0.7 MPa时，改变节流孔直径，将数据代入MATLAB中计算得出一组结果，同时利用该组设计进行节流孔及气膜建模，利用Fluent仿真模拟出一组结果，观察变化如图8所示，其中实线表示MATLAB计算结果，虚线表示Fluent计算结果。

由上图8可以看出，随着节流孔直径的增大，轴承的承载能力以及气膜刚度在不断减小，并且承载能力在轴承孔逐渐变大时，承载能力下降得越来越快。在进气口气压为0.5 MPa条件下，当节流孔直径增大到0.5 mm时，承载能力仅为13.1 N，轴承的承载能力过低，难以满足使用条件，节流孔直径不宜过大。

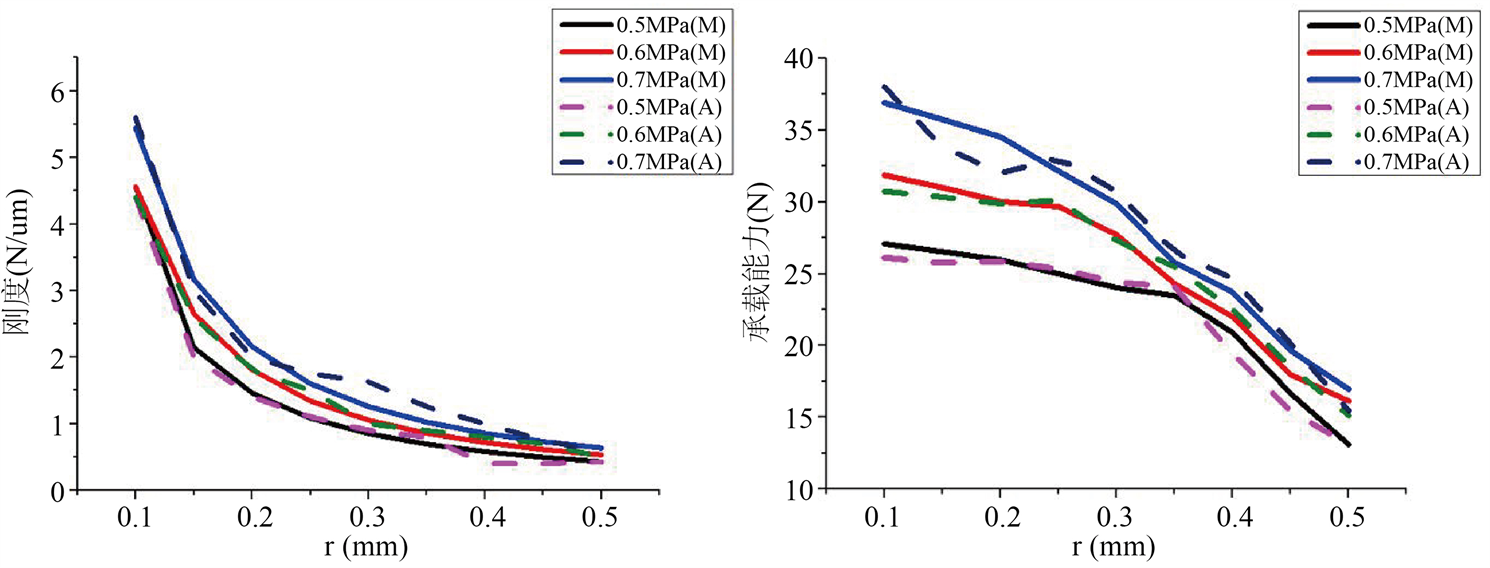
Figure 8. Influence of orifice diameter

图8. 节流孔直径的影响

5.2. 节流孔分布圆半径对轴承性能的影响

基本参数为轴承外径R1 = 17 mm；轴承内径R2 = 4 mm；节流孔直径为r = 0.1 mm；出气口压强与工作压强均为0.1 MPa；节流孔数为8个；分别在进气口压强为0.5 MPa，0.6 MPa，0.7 MPa时，改变节流孔分布圆半径，将数据代入MATLAB中计算得出一组结果，同时利用该组设计进行节流孔及气膜建模，利用Fluent仿真模拟出一组结果，观察变化如图9所示，其中实线表示MATLAB计算结果，虚线表示Fluent计算结果。

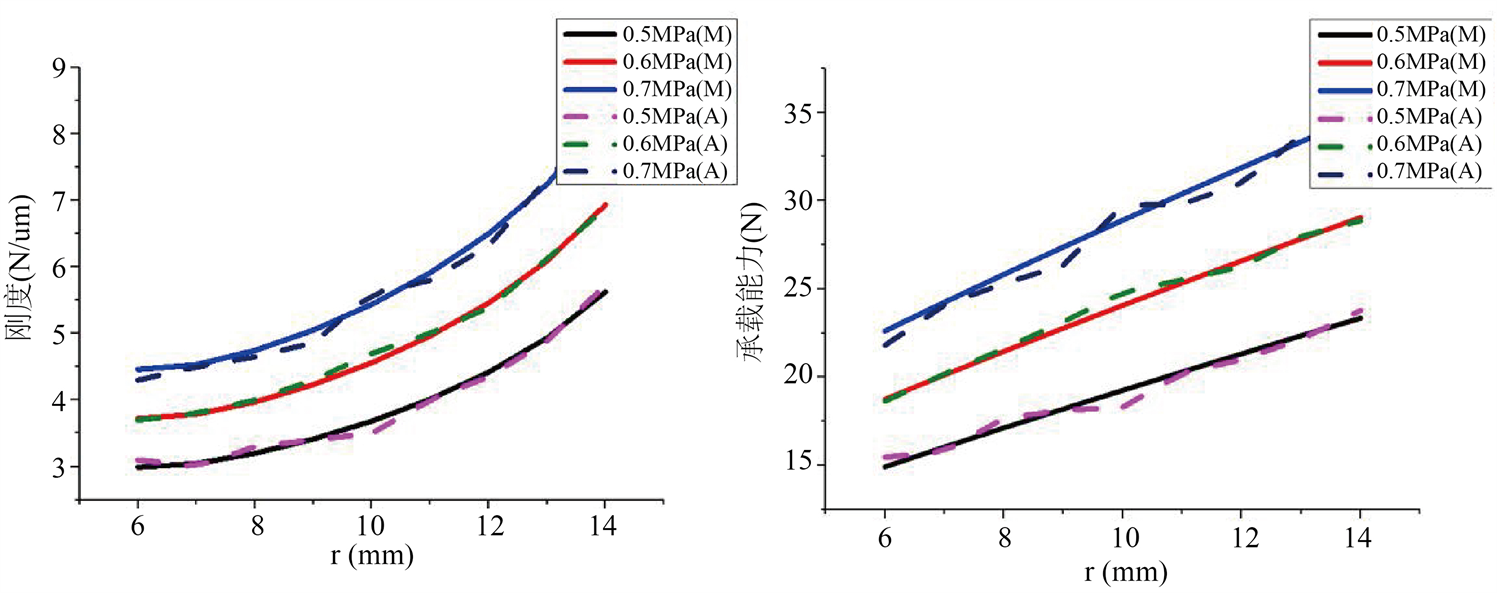
Figure 9. Influence of the radius and diameter of the orifice distribution circle

图9. 节流孔分布圆半径直径的影响

由上图9可以看出，随着节流孔分布圆半径值的增大，即节流孔分布圆越来越接近轴承外圆，承载能力与刚度都增大，并且承载能力大小与节流孔分布圆半径大小呈线性关系。在进气口气压为0.5 MPa条件下，当节流孔分布圆半径减小到6 mm时，承载能力仅为14.91 N，轴承的承载能力过低，影响电主轴的使用性能，节流孔分布圆半径不宜过小。

5.3. 节流孔数对轴承性能的影响

基本参数为轴承外径R1 = 17 mm；轴承内径R2 = 4 mm；节流孔直径为r = 0.1 mm；节流孔分布半径R0 = 10 mm；出气口压强与工作压强均为0.1 MPa；分别在进气口压强为0.5 MPa，0.6 MPa，0.7 MPa时，改变节流孔数，将数据代入MATLAB中计算得出一组结果，同时利用该组设计进行节流孔及气膜建模，利用Fluent仿真模拟s出一组结果，观察变化如图10所示，其中实线表示MATLAB计算结果，虚线表示Fluent计算结果。

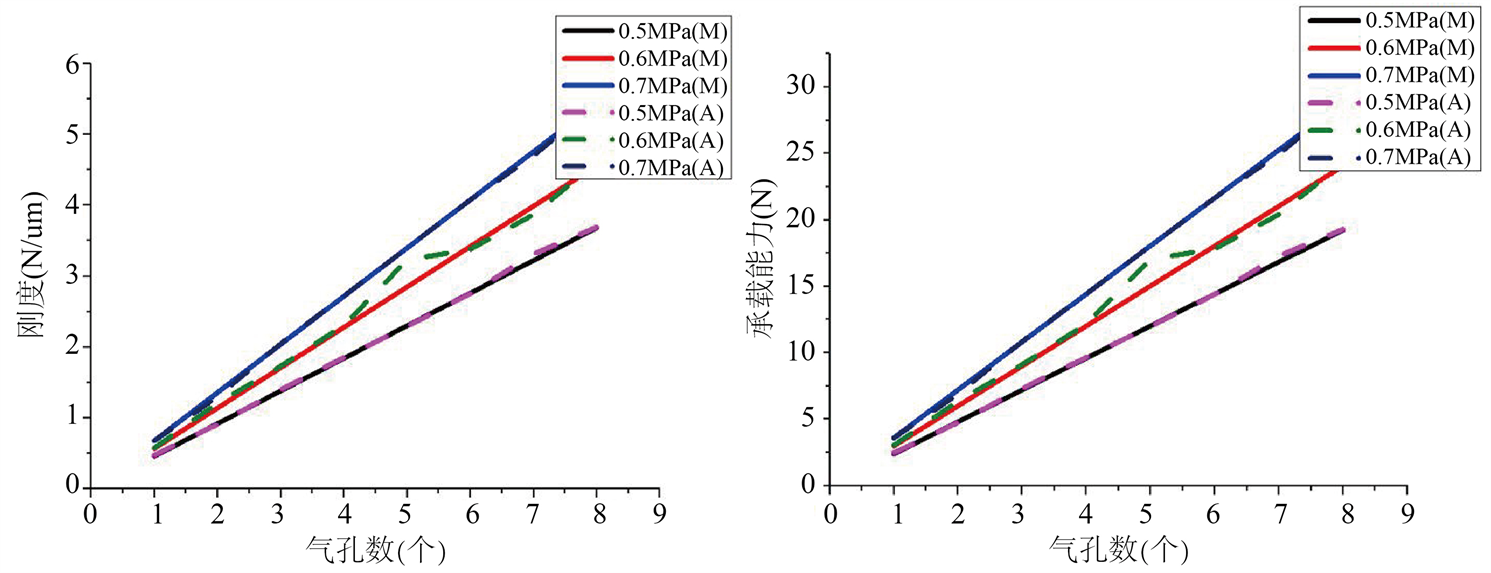
Figure 10. Influence of the number oforifice holes

图10. 节流孔数的影响

由上图10可以看出，随着节流孔数的增大，承载能力与刚度都增大，并且承载能力大小与节流孔分布圆半径大小呈线性关系，在几种情况之下，8个气孔数的轴承的承载能力以及刚度是单个气孔轴承的十几倍。节流孔数的增加能有限提高止推轴承性能。

Figure 11. Influence of inlet pressure

图11. 进气口压强的影响

5.4. 进气口压强对轴承性能的影响

基本参数为轴承外径R1 = 17 mm；轴承内径R2 = 4 mm；节流孔直径为r = 0.1 mm；出气口压强与工作压强均为0.1 MPa；节流孔数为8个；分别在节流孔分布圆半径为10 mm，11 mm，12 mm时，改变进气口压强，将数据代入MATLAB中计算得出一组结果，同时利用该组设计进行节流孔及气膜建模，利用Fluent仿真模拟出一组结果，观察变化如图11所示，其中实线表示MATLAB计算结果，虚线表示Fluent计算结果。

由上图11可以看出，进气口压强的增大，承载能力与刚度都增大，并且其大小均与进气口压强大小呈线性关系。但无论是在节流孔分布圆三种半径大小的情况下，进气压强为0.2 MPa时，承载能力均仅约为5 N，因此轴承的工作环境对轴承性能影响较大，使用时应特别注意进气压力等情况。

6. 结论

本文对电主轴的空气静压止推轴承进行设计分析，获得设计参数变化对于止推轴承性能的影响。主要研究结论如下：

1) 气膜厚度越小，空气静压止推轴承的刚度越高；但当气膜厚度小于10 μm时，轴承出气口速度达到了371 m/s，会产生音爆现象。

2) 节流孔数量及直径与轴承的节流孔内压强成正比关系，间接影响了静压止推轴承的性能，在节流孔数为8节流孔直径为0.5 mm时，加大进气口压强至0.7 MPa，轴承承载力仍不足20 N。

3) 进气口压强与轴承的刚度、承载能力成正比，且该条件对轴承性能影响最大。当进气口压强达到1 MPa时，该止推轴承能达到40 N以上的承载能力；当进气口压强仅为0.2 MPa时，此时轴承的承载能力仅为5 N左右。

基金项目

本课题研究受上海市级重点课程建设项目(2021378)及上海理工大学教改专项支持。

参考文献