基于行为编程的无人机导航系统研究

Research on Behavior-Based Programming for Unmanned Aerial Vehicle Navigation System

摘要: 针对当前复杂智能体系统设计耦合度高的问题，提出了一种在无人机导航系统中运用行为编程的方法，通过逐步构建无人机反应系统，实现无人机响应系统所期望的行为。该方法基于行为编程理论，将A-star算法与人工势场方法相结合，以减少系统间的耦合性，便于后续新功能的添加与维护。结果表明：本文提出的场景定义行为的方法，改变了传统无人机导航系统设计的现状。通过仿真实验和真实场景实验，对以行为编程为基础的无人机导航系统进行了验证，为其他智能系统在应用行为编程提供了实践基础。

Abstract: Aiming at the problem of high coupling degree in current complex agent system design, a method of using behavioral programming in the UAV navigation system is proposed. By gradually building the UAV response system, the expected behavior of the UAV response system is realized. Based on the theory of behavioral programming, this method combines the A-star algorithm with the artificial potential field method to reduce the coupling between systems and facilitate the subsequent addi-tion and maintenance of new functions. The results show that the method of scene definition be-havior proposed in this paper has changed the status quo of traditional UAV navigation system de-sign. Through simulation experiments and real scene experiments, the UAV navigation system based on behavior programming is verified, which provides a practical basis for other intelligent systems to apply behavior programming.

1. 引言

无人机(Unmanned Aeial Vehicle, UAV)是一种无人驾驶的飞行器 [1] ，它的飞行由车辆中的计算机自主控制，或在地面中的飞行员的远程控制下进行。除了与无人机联系最为紧密的军事应用外，无人机还有很多其他应用，包括军事侦察、边境巡逻、天气探测、抢险救援、科学探测等。无人机是一个复杂的综合系统，它将自主规划、环境感知等诸多功能糅合在一起。这些功能都能归结为无人机的导航功能。随着无人机技术的不断发展，人们对无人机导航系统的研究越来越深入。传统的无人机导航系统通常采用惯性导航系统、全球定位系统和磁力计等技术进行定位和导航 [2] 。然而，在很多复杂的环境下，如城市峡谷、森林等密集区域，GPS信号容易受到干扰，导致无人机定位精度下降，甚至失去定位。因此，研究一种能够适应各种环境并提高定位精度的无人机导航系统是非常必要的。

ROS (Robot Operating System) [3] 是由伯克利加州大学、斯坦福大学等机构联合研发的一种开放源代码的机器人操作系统。ROS提供了一系列工具和库，用于构建机器人应用程序，包括控制、感知、仿真、导航等方面。ROS提供了许多用于导航的功能包，如gmapping、amcl、move_base等，用户可以通过组合这些功能包来实现自己的导航系统，大大降低了导航系统的开发难度 [4] 。

自20世纪以来，越来越多的研究学者提出了软件危机的概念 [5] 。软件危机的出现主要是由于软件开发需求不断增长，而软件开发技术的进步却难以跟上需求的增长速度。2008年，David Harel提出了“解放编程”的概念 [6] ，他希望通过简单规范所需行为的方式，来开发复杂的软件系统。David Harel认为，软件的复杂性是因为需要交织许多同时发生的行为。研究人员希望使用类似于人类描述行为的方式来实现软件开发。David Harel等人于2011年提出了一种基于活动序列图(Live Sequence Chart, LSC)的Java软件开发的通用方法 [7] 。该方法将程序划分为多个模块，每个模块独立描述各自的行为。作者在后来的研究中称其为行为编程 [8] 。行为编程是一种新的编程范式，它可以提高系统的可维护性、可测试性和可扩展性。通过行为建模、状态机设计和规则引擎等技术，可以实现对系统行为的精细化描述和控制。行为编程可以使智能体自主完成任务，提高其自主性和独立性 [9] 。

本文认为，将行为编程和ROS机器人操作系统结合起来可以提高机器人的自主性，实现更灵活的机器人，加强机器人的安全性，并提高机器人的可维护性。行为编程可以使机器人在不需要人为干预的情况下自主完成任务，而ROS提供了一系列的导航、控制、感知等功能包，可以为机器人提供自主决策和执行任务的能力。本文基于行为编程理论，设计并实现了一种基于ROS的无人机导航系统。通过行为编程，该系统可以在仿真环境中实现高精度的无人机定位和导航，有效避免了传统导航系统在信号干扰和复杂环境下出现的问题。这为无人机的应用提供了更广阔的空间。本文还对该系统的性能进行了实验验证，结果表明该系统具有很好的鲁棒性。

2. 系统总体框架与模型建立

2.1. 总体框架

一般而言，无人机导航有多种实现方案。一种是最常见的基于惯性元件的惯性导航，这种导航系统一般都配有GPS辅助定位系统。这种惯性导航系统造价最便宜，应用的也最为广泛。然而，惯性导航是基于陀螺仪和加速度计来计算位置和速度的，因此在飞行器遇到外界干扰时，导航系统容易产生跳动或者抖动，从而影响飞航安全。另一种是通过即使定位与地图构建(Simultaneous Localization and Mapping, SLAM) [10] 算法实现。

通常来说，SLAM算法需要一台计算机处理图像和执行算法，再将计算结果发送给飞行控制器。数据处理的方案一般有两种，一种是由地面站的计算机处理。另一种是由无人机搭载微型计算机，由微型计算机进行处理，通过微型计算机的串行通信总线发送给飞行控制器。前者可以选择具有桌面级平台，数据处理能力大大提高。后者最大的优势是实时性好，飞行控制器和机载计算机通过串口连接，数据传输更加稳定。这种情况下使用机载计算机也能高速处理。因此本文选择机载计算机作为数据处理的方案。

为了降低无人机导航系统的耦合度，以避免将其设计成整体，而是采用模块化的设计思路。本文的研究对象涉及不同传感器之间的数据传输，为降低软件设计的复杂度，使用ROS进行开发。为了提高无人机操作系统的鲁棒性并解耦应用程序，本文将结合ROS操作系统和行为编程来开发无人机导航系统。

综上所述，本文使用激光雷达作为SLAM方案。采用GPS定位系统和气压计进行飞行高度控制。为了应对突发情况，采用图传一体的设备进行紧急控制。

2.2. 地图模型

本模板可直接用于论文及其文字的编排，有的页边距、行距、字体都严格符合规定，请勿修改！尤其是页边距，由于期刊在后期制作过程中需要在页眉、页脚添加各种信息，所以所有论文务必确保现有的页边距不被修改，页面空白不被占用。

机器人通过移动获得的环境信息，可以实现对地图的自动更新。一般情况下，一张地图并无一定的形状，它可能是一系列的点集，也可能是一种立体模型。根据机器人所要完成的任务，设计出了一种新的地图。在机器人应用中，一般将其划分为两类，即拓扑地图和度量地图。

(a) 拓扑地图与度量地图相比，拓扑地图的精度较低。两者的重点不同。在拓扑图中，只描述两个位置间的相互关系，不会考虑其他因素。这样的地图虽然简洁，但是却不能反映出周围的环境，也不能反映出周围的环境。拓扑图适用于简单的环境，但对于具有丰富信息的环境则难以满足需求。因此，如何利用拓扑地图对机器人进行自主导航仍然是一个亟待解决的问题。

(b) 度量地图 度量地图主要研究如何用一种准确的方法来表示环境中各种对象的空间位置关系可用于高精度定位的应用场合。根据所含环境特征的多少，可以将度量地图划分为稀疏图和密集图。稀疏地图通常只选择环境中具有特殊意义的特征进行表示，不需要表达所有环境特征，主要用于机器人的定位功能。稠密地图则相反，解析度越高，描绘的环境越详细。在二维地图上，这些小块经常以很多小正方形出现，而在三维地图上，它们就以很多小正方形出现。三维地图与二维地图相比，对系统的要求更高，因为它要保存每一片区域的位置信息，记录了很多冗余信息。

2.3. 行为编程模型

行为编程是一种软件开发方法，可将复杂任务分解为一组更简单、相对独立的行为来实现。行为线程是一种编程结构，用于控制和协调特定行为的执行，可能涉及多个对象和组件。通过同步和执行行为线程，可以产生集成的、有凝聚力的系统行为。行为编程是一种基于场景的编程方法，用于创造反应式系统的可执行规范。过渡系统可以用于定义和分析行为编程。

定义2.1 (过渡系统)过渡系统是一对关系，记为

$\left(Q,\to \right)$ (1)

其中Q是一组状态集， $\to$ 是Q上的一个二进制关系。在一个允许并行的系统中，对于一个给定状态的q，可能会有很多状态q，即 $\left(q\to q^{\prime }\right)$ 。当系统处于状态q时， $\to$ 表示每个操作都同时启用。

假设已经定义了一个带有标记的过渡系统 $\langle S,E,\to ,init\rangle$ ，其中S是一组状态集合，E是一组事件集合， $\to$ 是包含在 $\left(S\times E\right)\times S$ 中的过渡关系， $init\in S$ 是初始状态，这种过渡系统的运行符合以下形式： $s_0\stackrel{e_1}{\to }{s}_1\stackrel{e_2}{\to }\cdots \stackrel{e_i}{\to }{s}_i$ ，其中 $s_0$ 是初始状态，对于所有 $i=1,2,\cdots$ ， $s_i\in S$ ， $e_i\in E$ ， $s_{i-1}\stackrel{e_1}{\to }{s}_i$ 。

将行为线程定义为一个标记过渡系统，在这个系统中，每个状态下的事件都可以被标记为请求或标记为阻塞。给出一组行为线程的两个基本定理：1) 当且仅当某个行为线程轻轻且没有被任何行为线程阻塞时，事件才会发生。2) 当事件发生时，所有收到事件影响的行为线程都会发生状态转换 [8] 。

定义2.2 (行为线程)定义一个行为线程：

$\langle S,E,\to ,init,R,B\rangle$ (2)

其中， $\langle S,E,\to ,init\rangle$ 是一个标记过渡系统， $R:S\to 2^E$ 是将每个状态和行为线程请求的事件集关联起来的函数，即请求线程 $B:S\to 2^E$ 是将每个状态和行为线程阻塞的事件集关联起来的函数，即阻塞线程。

定义2.3(行为线程组)将一组行为线程

${\left\{\langle S_i,E_i,{\to }_i,ini{t}_i,R_i,B_i\rangle \right\}}_{i=1}^n$ (3)

的运行定义为下列的标记过渡系统的运行

$\langle S,E,\to ,init\rangle$ (4)

其中 $S=S_1\times \cdots \times S_n$ ， $E={\displaystyle {\cup }_{n-1}^i{E}^i}$ ， $init=\langle ini{t}_1,\cdots ini{t}_n\rangle$ ， $\to$ 表示过渡系统

$\langle s_1,\cdots ,s_n\rangle \stackrel{e}{\to }\langle {s^{\prime }}_1,\cdots ,{s^{\prime }}_n\rangle$ (5)

的转化，当且仅当

$\underset{e\text{isrequested}}{\underset{︸}{e\in {\displaystyle \underset{i=1}{\overset{n}{\cup }}{R}_i}\left(s_i\right)}}\wedge \underset{e\text{isnotblocked}}{\underset{︸}{e\notin {\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}\left(s_i\right)}}$ (6)

和

$\underset{i=1}{\overset{n}{\wedge }}\left(\left(e\in E_i\Rightarrow s_i\stackrel{e}{\to }{s^{\prime }}_i\right)\wedge \left(e\notin E_i\Rightarrow s_i={s^{\prime }}_i\right)\right)$ (7)

成立。

3. 行为线程实现

为了求出一条在一定条件下，由起点至终点的运动路径，必须采用一种全局路径规划方法。当前，最常见的全局路径规划算法有Dijkstra算法、Bellman-Ford算法、RRT (Rapidly-Exploring Random Tree)算法等。局部路径规划指的是当不能获得全局环境信息时，可以根据自己的状态和周边环境信息，实时地规划出一条不会发生冲突的理想的局部路径。常见的局部路径规划算法主要有动态窗口法、代价地图法、光线追踪算法等。针对这一问题，本文拟采用一种改进的航迹规划方法，在此基础上，并结合行为编程理论对路径规划进行优化。

本文首先利用A-star算法在全局范围内对无人机的飞航路线进行全局规划，以找到一条合理路径连接起点和终点。如果在此过程中无人机不断靠近障碍物，则利用人工势场法进行判断。人工势场法的优点是局部避障精度高，一定程度上能大大避免碰撞。但是，人工势场法容易出现极小值，即当无人机出现在障碍物较多的状态空间时，容易出现无人机无法移动的情况。在这种情况下，可以利用A-star算法让其恢复正常路径规划。

3.1. A-Star算法

A-star算法最早由Peter E. Hart等在1968年提出，主要是一种在静态路网中求解最短路径的图论方法 [11] 。它创意性的将BFS和Dijkstra等常规算法结合起来，实现了带有智能性质的启发式算法。首先根据定义确定估价函数大小，根据估计函数的大小确定最优路径。A-star算法在一个简单的图形的情况下，不仅可以达到BFS算法那样的运算速度，而且可以达到Dijkstra算法那样寻找到一条好的路径。A-star算法是一种广泛应用于图搜索和路径搜索的方法，常用A-star算法的估计函数可以表示为：

$f\left(n\right)=g\left(n\right)+h\left(n\right)$ (8)

其中n表示是当前节点， $g\left(n\right)$ 表示从起点到n的实际费用， $g^{\prime }\left(n\right)$ 代表当前节点与目标节点n之间的最小费用；而在特定的情况下，决策必须依靠启发性的信息。一般而言，曼哈顿距离是评价函数 $h\left(n\right)$ 最好的实现方法。则 $g\left(n\right)$ 和 $h\left(n\right)$ 的表示如下：

$g\left(n\right)=\min \left(\left|P_{T_n}{P}_{T_{n+1}}\right|\times V_g\right)$ (9)

$h\left(n\right)=\min \left(\left|P_{T_n}{P}_G\right|\times V_h\right)$ (10)

其中， $P_{T_n}{P}_{T_{n+1}}$ 表示从当前栅格节点 $P_{T_n}$ 到下一个方向栅格节点 $P_{T_{n+1}}$ 的直线距离。 $V_g$ 代表当前网格点到下一个方向网格点间的成本， $P_{T_n}{P}_G$ 代表从当前栅格节点 $P_{T_n}$ 到目标栅格节点 $P_G$ 的直线距离， $V_h$ 代表当前栅格节点与目标栅格节点间的代价值。

根据几何距离的计算方法，在网格图上计算出初始网格点对目标点的全局估计函数f(n)，其定义如下：

$f\left(n\right)=\min \left(\left|P_{T_n}{P}_{T_{n+1}}\right|\times V_g+\left|P_{T_n}{P}_G\right|\times V_h\right)$ (11)

当进行A-star算法路径规划时，需要考虑当前点到目标点代价值和起点到下一个目标点代价值。为了计算出权重，首先进行全局搜索，然后计算得到代价值，进而得到权重，最后选择权重最低的路径，运动过程中会实时计算出代价函数值，并判断是否最优解，若是则记录当前位置，否则继续寻找。A-star算法的执行依赖于两种基本集，即OPEN集和CLOSED集。其中，OPEN集合被用来存储要被检测的节点的信息，CLOSED集合被用来存储已经被选中且不需要再被检测的节点的信息。利用A-star算法中的代价函数公式，求出每一个节点的代价值，并将其存到打开集合中。之后，从开启集中选择出最小代价的节点，并将其存入关闭集，再以此节点为基础，不断地进行节点扩展，直至找到具有最小代价值的节点序列。

代价值更新运算的目的是保证每一个结点中所储存的父节点指针是从起始点到该结点的最佳路径。在A-star算法的节点扩充期间，每一个节点的父节点都被保存下来。这样，在找到一个目标节点之后，就可以对其进行反向追踪，从而获得最佳的节点顺序，也就是最佳的路径。

如图1所示，在利用A-star算法进行路径规划过程中，以格栅法建立地图模型。通过代价函数计算出代价值，将其存入第二章提到的OPEN集，从OPEN集合中选取代价最小的节点，并存入CLOSE集合。以CLOSE集合的节点为基础，拓展搜索范围，进行代价值更新。

Figure 1. Schematic diagram of A-star algorithm expansion

图1. A-star算法拓展示意图

由于A-star算法的核心部分取决于代价函数的实现，为了算法的通用性，本文使用欧几里得距离作为代价函数的实现。欧几里得距离被用作计算欧氏空间中任意两点的距离，且不限定规划目标的移动方向。规划目标可以任意角度移动。本文采用的距离计算方式如公式12所示。

$D\left(x,y\right)=\sqrt{{\left(x-x_t\right)}^2+{\left(y-y_t\right)}^2+{\left(z-z_t\right)}^2}$ (12)

其中， $\left(x,y,z\right)$ 和 $\left(x_t,y_t,z_t\right)$ 分别表示起点和终点的位置坐标，该公式计算起点和终点之间的距离，作为代价函数的值，用于A-star算法的路径搜索和规划。

为了方便展示，采用对欧氏空间投影的方式，因此，以欧几里得距离为距离计算方式的A-star算法二维路径规划的效果如图2所示：

Figure 2. Schematic diagram of two-dimensional path planning using A-star algorithm

图2. 使用A-star算法进行二维路径规划的示意图

根据上文的算法原理，本文采用的全局路径规划的步骤如下：

1) 定义OPEN和CLOSE集合，初始化各结点指针，将各个结点指针设置为NULL；

2) 初始化OPEN集合，将起点括入OPEN集合中，将当前节点的父指针指向起点；

3) 初始化CLOSE集合，将当前节点括入CLOSE集合中；

4) 搜索当前节点附近所有可行节点，按照公式(12)计算各个节点的代价函数。比较OPEN集合中的节点，如果存在，就比较各自的g(k)，如果该节点的值更小，就更新该节点的g(k)和f(k)，并将存储该节点的父指针指向该节点。如果OPEN集不存在该节点，就把该节点加入了OPEN集。如果目标节点被加入OPE集，就执行6)，否则执行5)；

5) 从OPEN集选取最小f(k)的节点，跳转至4)；

6) 从目标节点开始，通过父结点指针确定最终路径，路径规划结束，确定最终路径。

3.2. 结合人工势场法的A-Star算法

本文选择激光雷达作为飞行轨迹上障碍物的探测。激光雷达可以判断目标点与视觉传感器之间的距离，进而计算出距离值。因此，使用激光雷达可以有效地测量障碍物与无人机之间的距离，实现对飞行轨迹上障碍物的探测。本节提出了一种无人机路径规划方法，该方法基于A-star算法，通过节点和节点的几何距离来规划无人机的路径。实际飞行过程中，会存在动态障碍物影响飞行的情况，因此引入了人工势场法。此方法将势场函数加入到A-star的估价函数中，以引导无人机的运动，实现路径规划。估价函数为：

$f\left(n\right)=g\left(n\right)+h\left(n\right)+U\left(n\right)$ (13)

同时，本文采用了引力场和视觉传感器相结合的方式，判断无人机与前方目标之间的距离并执行规避操作，如图3所示。

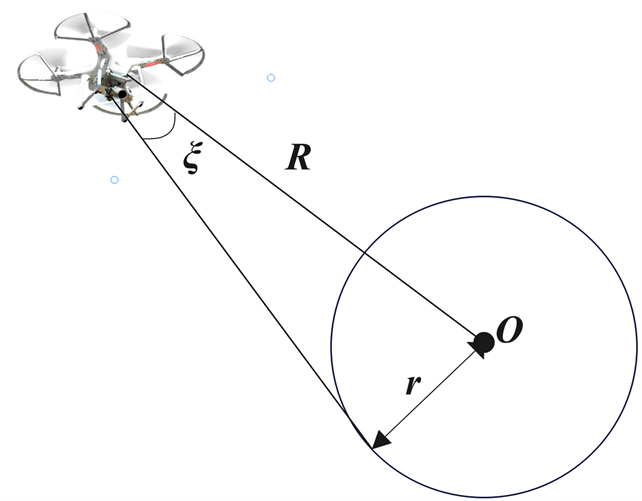
Figure 3. Schematic diagram of artificial potential field method

图3. 人工势场法示意图

该方法将无人飞行器与障碍物视为质点，提出了描述无人飞行器与无人飞行器间距离的两个重要参量R、r，并用来描述无人飞行器与无人飞行器间距离的两个参量。当无人飞行器的航迹满足R= r，则无人飞行器进入了一个临界势场范围。无人机的转动角为临界转动角，且此转动角满足：

$\sin \left(\xi \right)=\frac{r}{D}$ (14)

当无人机与障碍物的相对角度小于临界转动角时，表明无人机进入势场，此时认为碰撞风险。此时估价函数为公式12；当无人机与障碍物的角度大于时，表明无人机此时尚未进入势场，此时认为无碰撞风险，此时估价函数为公式8。在该策略中，当无人机接近障碍物时，障碍物对无人机的斥力就会增大，反之，则会减小。这种策略可以促使无人机远离障碍物，并确保其安全飞行。无人机在飞行过程中，所受的整体排斥力为各障碍物排斥力之代数之和，而整体排斥力的大小又决定了无人机在飞行过程中的运动方向。对于人工势场方法中存在的局部极小值、目标不可达等问题，本文采用A-star算法对目标进行二次定位，从而实现对目标的精确控制。在受到力较小或为0的情况下，无人机会进入局部极小状态，这时，依据障碍物的分布特征，利用A-star算法，在减小引力场的同时，对飞行路径进行再规划，使其脱离最小状态。本文拟将A-star算法与人工势场方法相结合，以A-star算法为研究对象，将人工势场方法引入到无人机路径规划中，并将其应用于无人机路径规划，以解决无人机飞行中存在的局部极小问题，同时保障飞行安全。改进后的算法流程图如图4所示：

Figure 4. Algorithm flowchart

图4. 算法流程图

4. 实验结果与分析

4.1. 仿真平台环境

本研究采用了基于PX4技术的机器人仿真软件Gazebo，对无人机进行了仿真。具体来说，可以在Gazebo中创建一个无人机模型，并将其与PX4连接，在ROS中启动各种机器人相关的功能和工具，例如传感器数据处理、导航算法、路径规划等，并编写控制程序，将控制指令发送给PX4，控制无人机在Gazebo中飞行。通过这种方式，三者协作起来形成了一个完整的无人机仿真系统。通过这种方式，Gazebo提供了一个真实的仿真环境，ROS提供了各种机器人相关的功能和工具，PX4提供了无人机的飞行控制和导航功能，三者协作起来形成了一个完整的无人机开发者平台。包括Gazebo在内的所有仿真器都使用MAVLink API与PX4进行通信。该API定义了一组MAVLink消息，用于向PX4提供来自仿真环境的传感器数据。图5的(a)、(b)展示了仿真环境下飞机起飞和降落的示意图。

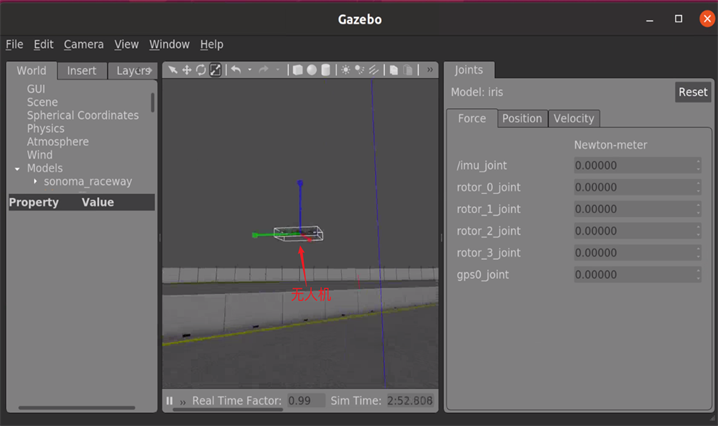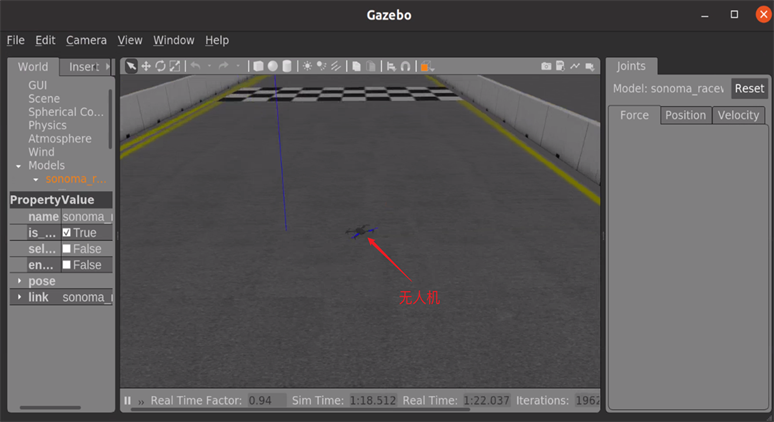(a) (b)

Figure 5. Simulation environment diagram. (a) Take-off diagram; (b) Landing diagram

图5. 仿真环境图。(a) 起飞示意图；(b) 降落示意图

4.2. 可视化显示平台

为了实时显示ROS中的消息内容，本文旋转Rviz作为无人机飞行实验的可视化平台。为了符合飞行实验的要求，需要对Rviz进行重新设计。Rviz是一款对 ROS消息进行可视化处理的软件，它支持多种数据类型。

本文按照以下步骤对Rviz界面进行设计和开发：

a) 添加一个Fixed Frame：Fixed Frame是Rviz的参考坐标系，用于指定可视化数据的基准坐标系。本文选择惯性测量单元(IMU)下的跟随坐标系或者世界坐标系，然后在Rviz的左下角添加一个Fixed Frame，并将其设置为所选坐标系。

b) 添加TF数据：TF是ROS中的一个重要功能模块，用于管理坐标变换。本文将自定义的TF数据通过ROS传输到Rviz，然后将其可视化。为此，可以使用ROS中的tf2_web_republisher package，将TF数据转换成Websocket格式，然后在Rviz中加载visualization_marker_array节点来显示所需的坐标系和其间的变换。

c) 添加无人机模型：本文将无人机的模型加载到Rviz中以便查看其位置和姿态。可以使用ROS中的robot_model包，将模型文件转换为URDF格式，并加载到Rviz中。此外，还可以使用ROS中的mavros包，将无人机的状态数据与Rviz相连，实现无人机模型的实时更新。

d) 添加无人机轨迹：本文需要在Rviz中显示无人机的轨迹，以便分析其飞行情况和测试结果。可以使用ROS中的visualization_msgs，发布一系列离散点的轨迹信息，并在Rviz中加载trajectory消息。

e) 添加参考指令：本文需要在Rviz中显示通过板载计算机下发的参考指令。可以在ROS中发布所需的参考指令，并在Rviz中加载visualization_marker消息，以在Rviz界面上显示参考指令。

通过以上步骤的实现，就可以在Rviz中实时显示无人机的飞行状态，方便进行测试和分析，如图6所示。

4.3. 导航实验分析

4.3.1. 可行性实验

实验以无人机导航系统中的行为线程集为研究对象，对其优势进行研究。在该试验中，我们使用了控制变量法，来观察该系统是否实现了无人机的导航功能。其中，第一组实验没有添加行为线程，设置了障碍物，实验结果表明该应用程序能够正常工作，但是无法完成导航功能。第二组实验中，增加了行为线程同时设置了障碍物，测试表明该应用程序可以正常工作，同时导航功能也可以实现。第三组实验

Figure 6. Simulation environment diagram

图6. 仿真环境图

没有设置障碍物，同时没有添加行为线程，测试的结果表明，该软件能够正常工作，但是其导航功能并没有得到满足。第四组实验中，添加了行为线程，但同时去除了障碍物，此时程序可以正常执行，导航功能也可实现。实验结果如表1所示。

Table 1. Feasibility test results

表1. 可行性实验结果

基于上文的实验结果表明，行为线程不影响应用的正常运行，即应用程序不会因为行为编程的加入而影响。这证明了行为编程理论应用到无人机导航系统是完全可行的。

4.3.2. 性能试验

实验一共进行了500次，采用Shell脚本触发运行，根据仿真系统记录的日志对性能指标进行统计，得出了表2。

Table 2. Performance test results

表2. 性能实验结果

通过对表2的数据分析，可以得出：与其他编程方法相比，基于行为线程的编程方法具有较短的平均导航时间和较快的平均仿真完成时间，从而表明其更为高效。就CPU占比而言，行为编程方法更高。这说明行为线程可以充分利用自身天然多线程的优势，如在加载GUI时同时检测障碍物位置，两者互不干扰。而剔除了行为编程方法以后，无法充分利用多线程，导致了仿真时间更长，同时也无法充分利用CPU，导致CPU的利用率不高。就仿真成功率而言，行为编程方法也更具优势。就两者的平均里程计数据而言，说明应用了行为编程的导航系统更加高效。

5. 结论

本文在无人机导航系统中引入了行为编程，并采用行为编程对无人机导航系统进行了设计与实现，将其划分为导航控制线程和路径规划线程。同时，本文将A-star全局路径规划算法和人工势场局部路径规划算法相结合，以充分利用各自的优缺点。使用行为编程方法，成功降低了导航系统的耦合度，从而方便了新功能的添加和维护。本文通过仿真环境的测试实验，验证了行为线程的可行性和性能优势。