1. 引言
汽车的轻量化对于节能环保具有重要的意义。欧洲铝业协会根据大量的研究数据进行分析,得出以下结论:当汽车的整车重量下降20%时,汽车油量的消耗可以减少20%,能源的效率将会升高10%~18%,尾气的污染物排放量会减弱10%~12% [1] 。此外,汽车质量每减少100 kg,每升油可多行驶1 km。而白车身是汽车的基础,质量占整车的40%左右,因此对白车身展开轻量化研究已经成为当今汽车行业的重要研究课题。安徽理工大学的王小睿通过结构优化设计白车身的轻量化方案,减少了部分零件的料厚,优化部分零件的形状、尺寸,基本实现了减重目标 [2] 。重庆理工大学的王权局部采用结构尺寸设计、平台CMAN选型设计、安装结构轻量化设计使白车身减重,并基于灵敏度分析对白车身板件进行尺寸优化 [3] 。天津科技大学的李义东首先确定哪些板件对白车身动态特性的修改最为有效,根据灵敏度分析结果确定以20个相对敏感的板件作为优化对象。然后通过尺寸优化及牛顿法获得板件最优厚度值。最终提升白车身一阶扭转模态频率的同时降低白车身总质量 [4] 。Duan Li Bin提出了一种基于厚度的子域混合元胞自动机(T-SHCA)算法来解决侧面碰撞下白车身的轻量化设计,并基于高效的全局优化算法对某白车身厚度进行了优化,验证了其收敛性和高效性 [5] 。
近似模型拟合方法是通过将试验设计得到的样本点输入与响应输出拟合成为高精度的数学模型,来逼近设计变量与响应的关系。由于白车身轻量化需要考虑模态、刚度等多个性能,而直接调用有限元模型进行迭代分析,需要耗费大量时间。因此本文采用代理模型技术和有限元分析相结合的方法。首先采用灵敏度分析方法来分析车身板件厚度对质量、弯曲刚度、扭转刚度、一阶弯扭频率的灵敏度程度,由此计算相对灵敏度并进行排序,从而选择优化设计变量。进而通过HyperStudy软件,通过哈默斯雷采样法采样,并进行拟合,最后通过拟合的响应模型结合GRSM优化算法多次迭代获得Pareto最优解集,从而得到最优轻量化方案。
2. 白车身建模及性能分析
2.1. 车身有限元建模
本文基于HyperMesh建立某车型白车身有限元模型,如图1所示。车身板件采用以四边形为主的壳单元进行网格划分,焊点采用ACM单元,胶体采用实体单元。整个有限元模型单元总数为784,267,节点数为896,790,总重量为0.3645吨。本文的主要研究目的是通过尺寸优化达到白车身的轻量化目的,所以白车身钣金件材料都赋予普通钢材。其车身主要材料及其对应参数如下表1所示。
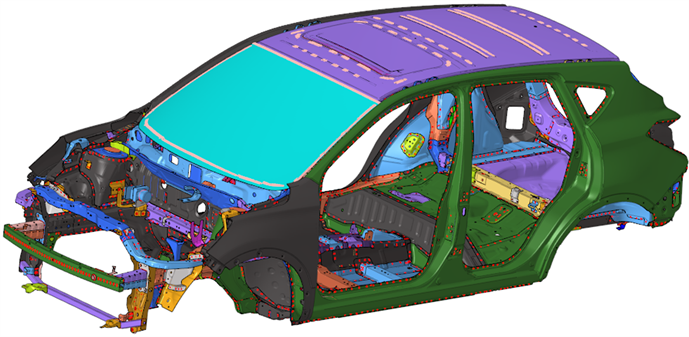
Figure 1. Body in white finite element model
图1. 白车身有限元模型
2.2. 自由模态分析
对车身的模态分析是指通过研究整车及车身局部零部件的振型及各阶固有频率 [6] ,进而对局部结构进行修改,以改变其振型,避免汽车在使用过程中产生共振,起到降低噪声提高舒适度的作用 [7] 。白车身结构模态分析要求计算模型不添加任何约束和加载,分析结果得到的是自由模态。本文采用optistruct求解器研究其模态振型,由于对白车身振动响应的影响较大的激励多集中在低频域,故本文仅研究前6阶模态。其振型图如图2~图7所示,其振型和频率数值如表2所示。
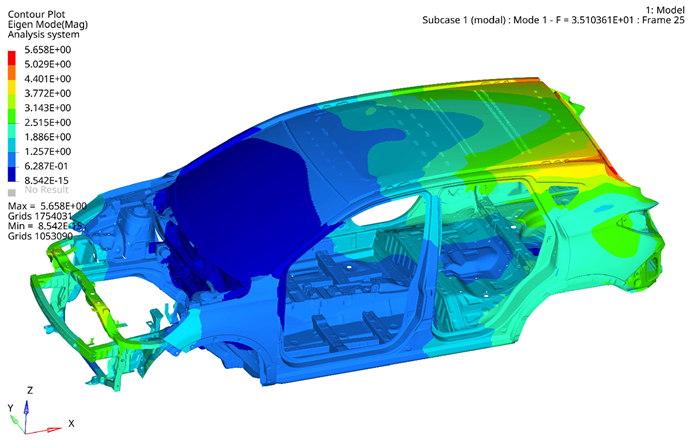
Figure 2. Body-in-white first-order modality
图2. 白车身一阶模态
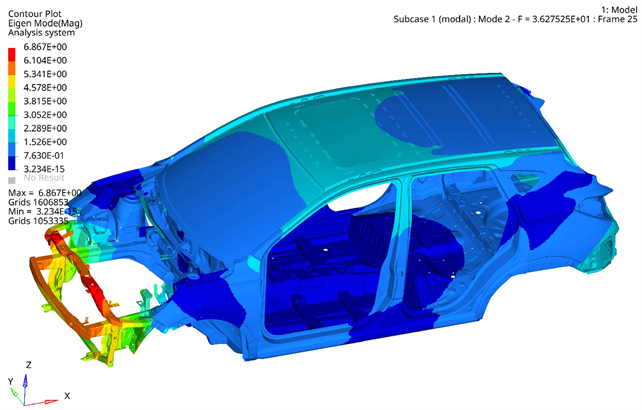
Figure 3. Body-in-white second-order modality
图3. 白车身二阶模态
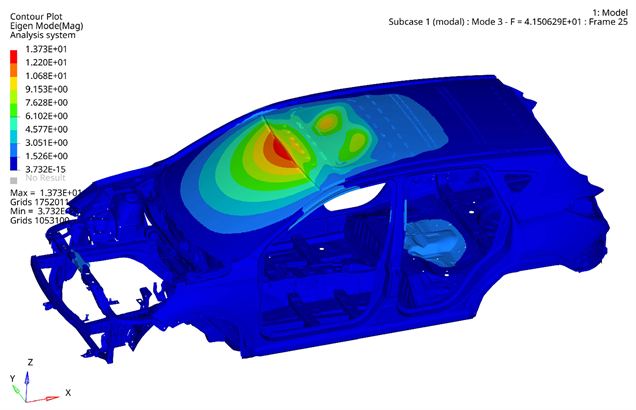
Figure 4. Body-in-white third-order modality
图4. 白车身三阶模态

Figure 5. Body-in-white fourth-order modality
图5. 白车身四阶模态

Figure 6. Body-in-white fifth-order modality
图6. 白车身五阶模态

Figure 7. Sixth-order mode of body-in-white
图7. 白车身六阶模态

Table 2. Free mode shape and frequency
表2. 自由模态振型及频率
2.3. 白车身弯曲刚度分析
白车身弯曲刚度体现了车身抵抗垂向载荷作用下发生弯曲变形的能力 [8] 。在有限元模型中弯曲工况边界条件为:约束左前减震塔中心点Y向、Z向平动自由度,约束右前减震塔中心点Z向平动自由度,约束左后减震塔中心点X向、Y向、Z向平动自由度,约束右后减震塔中心点X向、Z向平动自由度 [9] 。载荷条件为:在前后减震塔中心线对应的门槛梁上各施加Z向负1000 N的力。白车身的弯曲刚度Kb通常用车身收到的总载荷F与加载点在受力方向上的最大位移Zmax的比值来表示,其计算公式如式
(1)
根据加载后的位移云图如图8得到加载点的位移分别为−0.173 mm和−0.177 mm,并由此计算出最大位移Zmax为−0.175 mm,代入式(1)可得弯曲刚度为11428.5714 N/mm。
2.4. 白车身扭转刚度分析
白车身扭转刚度是衡量车身抵御垂直反向载荷作用下发生结构扭转变形的能力,是车身扭转性能的体现。在有限元模型中扭转工况边界条件为:约束左后减震塔中心点X向、Y向、Z向平动自由度,约束右后减震塔中心点X向、Z向平动自由度,约束前保险杠中间点Z向平动自由度。载荷条件为:根据扭矩值Mr为2000 N∙m,左右减震塔的中心距离L为1181.937 mm,在前处左右减震塔分别施加Z向相反方向的1692.138 N的力。白车身的扭转刚度Kt通常用车身所加载荷的扭矩值Mr与轴间相对扭转角θ的比值来表示,其计算公式如式(2)所示:
(2)
轴间相对扭转角θ的计算公式如(3)所示
(3)
式中,d1、d2分别是左右减震塔加载点的Z向位移,L是左右减震塔的距离。
根据加载后的位移云图如图9,得到加载点的位移分别为1.227 mm和−1.232 mm,将数值代入式(2)式(3)中,得到了扭转角为0.1192˚和扭转刚度为16778.5235 N∙m/˚。
3. 白车身灵敏度分析
灵敏度是指某一个响应的数值随着某一设计变量变化的比率。在工程中,为了准确衡量车身某个板件对整个车身的性能参数的重要程度,从而做到为了某一目标合理选择变量进行调整,常常在优化前引用灵敏度分析进行筛选变量。
由于整个白车身是由数百个板件连接而成,而对其全部部件都纳入轻量化研究要开展的工作量巨大,因此选择灵敏度分析找出对车身结构性能影响小、质量影响大的部件进行优化,可以有效提高效率。本文通过HyperMesh设置,研究板厚对白车身质量、弯曲刚度、扭转刚度、一阶弯曲频率、一阶扭转频率的灵敏度值。
由于本文中灵敏度分析的结果类型较多,不能准确直观的筛选出需要的变量。因此,根据灵敏度分析结果分别计算各响应的相对灵敏度。一阶弯扭频率、弯曲刚度、扭转刚度的相对灵敏度计算公式如下 [10]
(4)
(5)
(6)
(7)
式中,S为相对灵敏度函数,L为灵敏度函数,f1、f3、Kb、Kt、m分别为一阶扭转频率、一阶弯曲频率、弯曲刚度、扭转刚度、质量 [11] 。
各板件的相对灵敏度如表3所示。相对灵敏度的绝对值越大,表示增加同样的板厚,质量增加的同时,白车身性能受到的影响越大,反之则越小。相对灵敏度的数值为正,则质量与白车身性能为正相关,反之则为负相关。本文的研究目的是使白车身在自身性能满足要求的同时,达到质量最小。因此根据相对灵敏度计算的结果,选择弯曲刚度相对灵敏度绝对值小的部件,并且去除部分弯曲扭转频率、扭转刚度相对灵敏度绝对值大的部件,最终筛选出前15组变量。

Table 3. The relative sensitivity of each plate
表3. 各板件的相对灵敏度
4. 基于响应面的白车身多目标优化
4.1. 试验设计
试验设计(Design of Experiment, DOE),也称为实验设计,是通过在设计空间中选取一定数量的样本点进行研究的方法。想要建立近似模型,首先就需要用DOE方法采取一定数量的样本点,从而构建样本点数据。因此,选择合适的DOE采样方法是得到理想试验结果和构建高精度近似模型的前提。目前常见的试验设计方法有可扩展格栅序列法、拉丁超立方法、哈默斯雷采样法等。
考虑到白车身研究是非线性问题,而哈默斯雷采样适用于响应面为高度非线性的情况,是采用伪随机数值发生器均匀地在一个超立方体中进行抽样,可以在k维立方体上取得较好的均匀分布,因此本文采用哈默斯雷采样法。哈默斯雷采样法最少的采样次数是
,N为设计变量的个数。针对上节中灵敏度分析筛选出的15个厚度变量,本文采样150次。设置上下限为初始厚度的±0.3,对某些下限超过0.5的,由于一般制造工艺要求钣金件最小尺寸为0.6,将下限值修改为0.6。优化设计变量表如表4所示:
4.2. 响应面拟合
通过近似模型拟合方法可以将试验设计得到的样本点拟合成高精度的数学模型,来逼近设计变量与响应的关系。从而达到通过拟合模型来代替真实模型,直接改变设计变量快速获得响应的估计值,而不需要耗费大量资源去重新计算真实模型 [12] 。而选择合适的拟合算法是拟合模型的关键。
常见的拟合算法有最小二乘法(LSR)、移动最小二乘法(MLSM)、径向基函数(RBF)、HyperKriging等。本文采用HyperStudy集成的FAST (Fit Automatically Selected By Training)功能,自动从LSR、MLSR、RBF等中选择对各响应拟合精度最好的方法进行拟合。最后各个响应采用的拟合方法如下表5。
完成拟合的模型需要通过查看各个响应的复相关系数R-Square (R2)来评价模型的精度,R2越接近1,说明模型越准确。本模型的各个响应的R2如下表6所示,都大于0.9且无限接近1,证明拟合精度非常好,可用于后续的计算 [13] 。

Table 5. Response variable fitting method
表5. 响应变量拟合方法

Table 6. Response surface accuracy evaluation table
表6. 响应面精度评价表
选择任意两个设计变量和单个响应可以通过三维图表达三者的响应面关系。本文的设计变量和响应参数过多,无法直接观察到所有参数的响应面关系,因此仅选择其中两个变量为例观察其响应面模型。如图10~图14所示,x轴为变量var_440的厚度变化范围,y轴为变量var_441的厚度变化范围,z轴为对应的各响应值的变化范围。
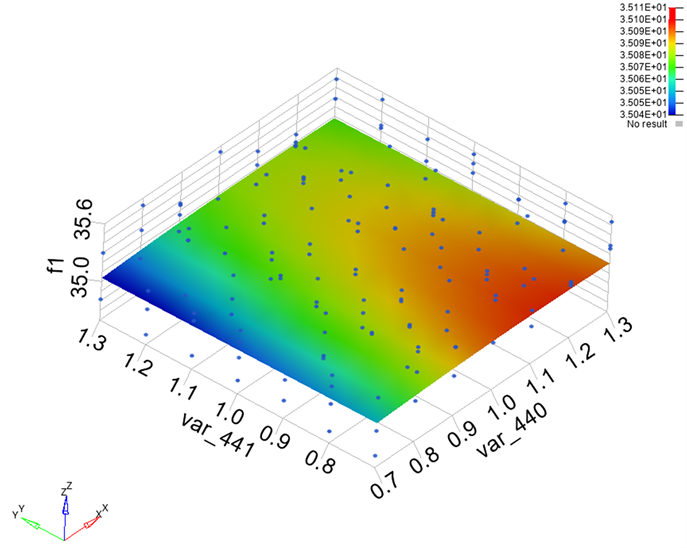
Figure 11. First-order torsional frequency response surface model
图11. 一阶扭转频率响应面模型
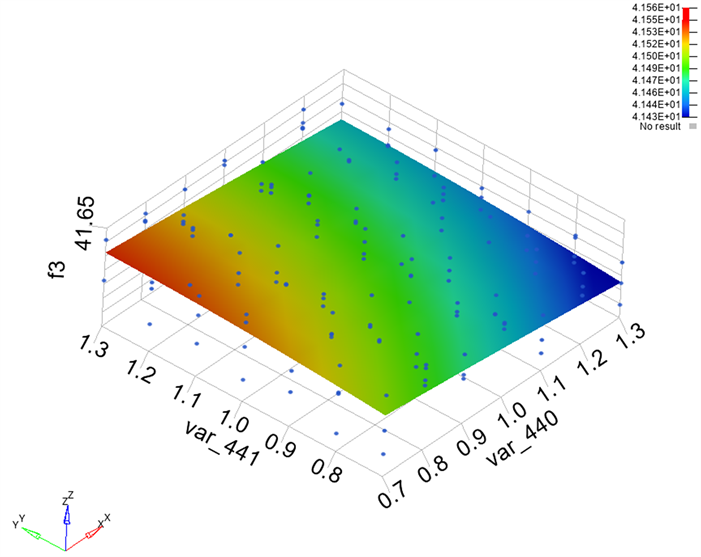
Figure 12. First-order bending frequency response surface modelsurfaceforce
图12. 一阶弯曲频率响应面模型
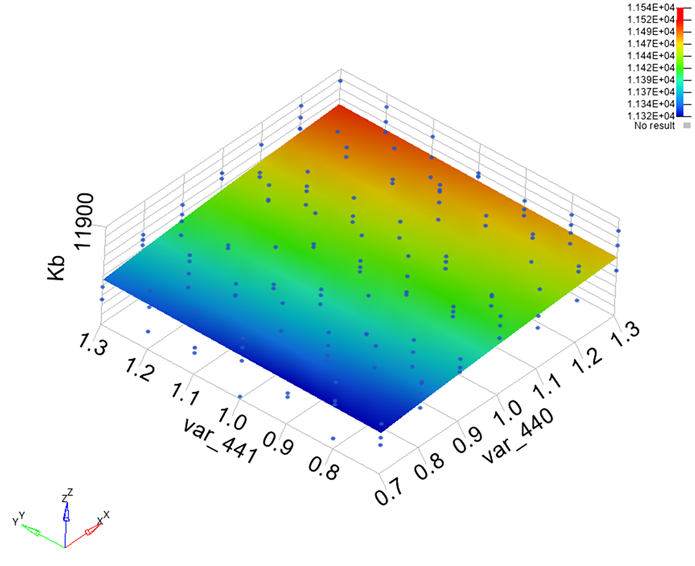
Figure 13. Model of the bending stiffness response
图13. 弯曲刚度响应面模型
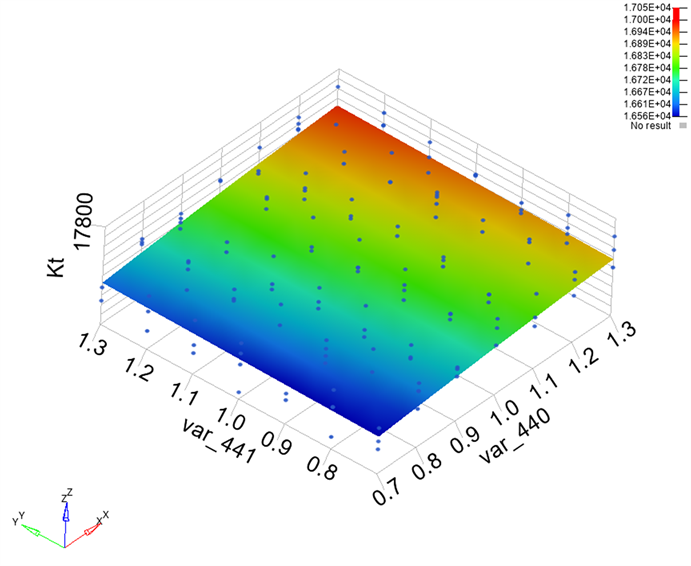
Figure 14. Torsional stiffness response surface model
图14. 扭转刚度响应面模型
4.3. 多目标优化
常见的优化算法可以分为三类:基于梯度的算法、基于响应面的算法、探索性算法。基于响应面的算法在迭代中不断构建和更新响应面,利用响应面来寻找最优解,主要有ARSM-自适应响应面法、GRSM-全局响应面法、SRO-系统可靠性优化。其中GRSM-全局响应面法是一种在优化过程种不断进化的算法,它是多目标优化问题的默认算法,具有全局搜索的能力,因此在很多优化问题上表现不错,尤其在设计变量的个数较多时效率较高 [14] 。
本文以车身质量最小,弯曲刚度最大为目标函数,以一阶弯扭频率和扭转刚度为约束,采用GRSM算法对白车身进行轻量化设计,构建数学模型如下:
(8)
式中:m为白车身质量,Kb为弯曲刚度,Kt为扭转刚度,f1为一阶扭转频率,f3为一阶弯曲频率,var_440、var_441,……var_454为部件厚度。
在HyperStudy中设置相应参数,经过500次寻优迭代,得到其Pareto解图如图15所示。
从Pareto解图可以看出,白车身质量和弯曲刚度这两个目标是矛盾的,白车身整体弯曲刚度越高的方案对应的白车身质量也随之而增加,而如果想要大幅减小车身质量,必然会导致整体的弯曲刚度大幅减小。因此综合考虑车身轻量化要求,选取第312次迭代结果为最优解。其各个变量参数如表7所示,可以看出优化后各个板件的厚度都有了不同的变化,后期将对优化后的变量值重新提交计算,验证轻量化方案。

Table 7. Comparison of values of variables before and after optimization
表7. 优化前后变量数值对比
4.4. 轻量化方案性能验证
按照迭代最优结果中各变量的数值进行修改有限元模型,再次计算白车身的质量、模态、弯曲刚度、扭转刚度。将优化前后的结果进行对比得到表8所示。

Table 8. Comparison of results before and after optimization
表8. 优化前后结果对比
5. 结论
本文采用了灵敏度分析方法来筛选出合适的变量进行优化,避免了变量选择的盲目性。综合考虑了白车身的多种性能指标,基于HyperStudy建立了高精度的响应面模型,用简单的响应面模型代替真实有限元模型。在保证刚度、一阶弯扭频率性能的前提下,进行了白车身质量最小化弯曲刚度最大化的多目标优化,最终获得了Pareto最优解集。根据优化目标选择一个较为合适的设计方案,在刚度、模态等性能参数满足要求的同时,实现白车身减重3.7%,基本实现轻量化目标。本文的研究方法和研究思路可以大大减少白车身所需要的开发时间和成本,为白车身轻量化研究提供指导意义。
NOTES
*通讯作者。