1. 引言
持续荷载作用下,混凝土在初始变形的基础上,随着时间推移会产生新的变形增加(徐变)。徐变有自由、约束徐变。纯混凝土静定结构产生的是自由徐变。结构中混凝土,受到钢筋或钢材约束,产生的是约束徐变。徐变除受时间(加载龄期、计算龄期)、混凝土自身因素(如水胶比、骨料)的影响,还受钢筋或钢材等约束的影响。
为简化计算,工程中常用混凝土弹性模量折减一半的方法考虑徐变 [1] ,这种处理方式简便易行,但较为粗糙,没有考虑钢筋或钢材约束的影响,对早龄期加载、环境干燥、持荷时间长等情况偏于不安全,而情况相反时又偏于保守,因此须有更精确的简化计算方法。这对徐变敏感结构尤为重要,如斜拉桥悬臂法施工过程中收缩徐变的影响 [2] ;高层建筑结构收缩徐变引起混凝土核心筒与外部钢框架之间的竖向变形差问题 [3] ,在施工过程中楼层重力荷载逐步加载,可能出现数值分析迭代不收敛等难题。若要精确计算徐变较为复杂,目前研究主要采用数值方法 [4] 。文献 [5] 基于徐变积分本构给出了一种随着时间逐步迭代计算较为精确的数值方法,文献 [6] 给出了钢筋混凝土轴心、偏心受压柱收缩徐变对最小配筋率影响的数值方法。为此,本文考虑配钢影响,以及混凝土受常量、变量荷载作用,对徐变换算弹性模量的设计参数开展了解析法研究,基于徐变微分本构关系推导了徐变调整系数ψ的计算公式,为ψ的进一步简化提供了理论依据。
2. 纯混凝土的徐变换算弹性模量
2.1. 考虑滞后弹性应变的修正
自1937年Dischinger [7] 首次应用以来,采用徐变微分本构关系在工程结构中应用广泛,其优点是能够推导出各种徐变问题的解析解,将徐变非线性有限元数值分析转化为弹性分析。Dischinger法仅需一条徐变系数曲线(母曲线),便可得到不同加载龄期的全部曲线。换句话说,Dischinger法中徐变系数时间自变量仅有计算时间(t),省去了加载龄期(t0)。
通常徐变系数模型包括t、t0两个自变量,如按照MC2010 [8] 徐变系数模型,假定加载龄期分别为28、60天,可以得到两条曲线,1000天徐变系数分别为1.47、1.2 (见图1),可将其设定为精确解(因为MC2010是在实验数据回归分析后得到的模型,经历了30多年各种版本的修正,在世界范围内获得了较多的认可)。然而在实际工程中,结构中的混凝土应力总是不断变化,应力增量对应的加载龄期在不断变化,徐变系数与加载龄期之间是非线性关系,解析分析难度大。如果将加载龄期省去,则可以推导出各种徐变效应的解析解,由此Dischinger法应用具有重要意义。如图1所示,将加载龄期28天的MC2010曲线作为母曲线,向下平移,得到龄期60天的Dischinger法曲线。
显然,Dischinger法曲线低估了晚龄期加载混凝土的徐变。应用叠加原理时,如果应力递减变化,Dischinger法会高估徐变,如果应力递增变化则会低估徐变。
为此,Rüsch对此进行了改进,考虑滞后弹性应变对弹性模量和徐变系数进行了修正 [9] 。Rüsch依据混凝土徐变的卸载试验结果,将徐变分为滞后弹性应变和徐塑应变两个部分,滞后弹性徐变系数为0.4,徐塑徐变系数与Dischinger法相同。这样,将Dischinger法曲线向上平移0.4,便得到了Rüsch法曲线,如图1所示。从图1可以看出,Rüsch法曲线与MC2010曲线吻合较好。MC2010曲线是基于试验数据回归得到的模型,应用广泛,精度较高。因此,有必要推导基于Rüsch法的混凝土弹性弹性模量和徐变系数的修正后的公式。
滞后弹性应变发展较快,一般在3个月内完成,如图1所示90天之后,Rüsch法曲线与MC2010曲线几乎重合。因此,在力学分析时可将滞后弹性应变与瞬时弹性应变合并计算,剩下的徐塑应变按照徐变微分本构计算 [10] 。
滞后弹性应变约为0.4倍瞬时弹性应变(
, t0为加载龄期),合并后弹性应变为
,这相当于将混凝土弹性模量(Ec)进行了折减,折减修正后混凝土弹性模量
(1)
徐变是混凝土在压应力作用下随着时间发展所增加的变形,徐变后混凝土应变(
)与时间(t)之间的关系为:
(2)
其中,φ为徐变系数。
则考虑滞后弹性应变修正后徐变系数为
(3)
2.2. 常量荷载情况的有效弹性模量
钢筋混凝土桥梁等结构自重较大,恒载徐变计算是最重要的一种工况。将混凝土徐变构件等效为一种弹性材料,是工程结构实用计算的重要方法。用徐变换算弹性模量表示等效后的材料特性,则可以按照弹性方法计算应变,当荷载为常量时应变表示为
(4)
其中,徐变换算弹性模量
,徐变折减系数
,N0为轴力,Ac为横截面面积,如图2所示。
需要说明的是,式(4)也就是有效模量法,由此说明有效模量法的假定有:① 荷载为常量;② 对象是没有考虑配钢的纯混凝土。本文是在有效模量法的基础上进一步考虑变量荷载和配钢的影响。
2.3. 考虑变量荷载的弹性模量修正
结构中的混凝土除了受到恒载作用,还受随时间变化的荷载作用。荷载随着时间单调递增变化是一种重要的工况,如逐步增加的楼层重力荷载、超静定结构徐变引起的次内力。此工况如图3所示可以假定与徐变系数成线性关系,即
(5)
其中,系数k是常量。
应变与荷载和徐变系数两个变量有关,按照徐变微分本构,应变的微分增量为荷载的微分增量与徐变系数的微分增量之和,即有
(6)
按照定解条件(
,
)得
(7)
因此,弹性模量折减系数
(8)
其中,弹性模量调整系数ψ反映了荷载单调递增变化对折减系数的影响。
3. 考虑配钢的弹性模量修正
3.1. 常量荷载的情况
钢筋或钢材是影响徐变的主要因素。混凝土在应力作用下产生徐变,钢不产生徐变,混凝土徐变受到钢的阻碍产生相互约束力。仅考虑轴向徐变时截面配钢可进行如图4所示的简化。配钢系数为对称钢筋混凝土与型钢混凝土的统一模式。
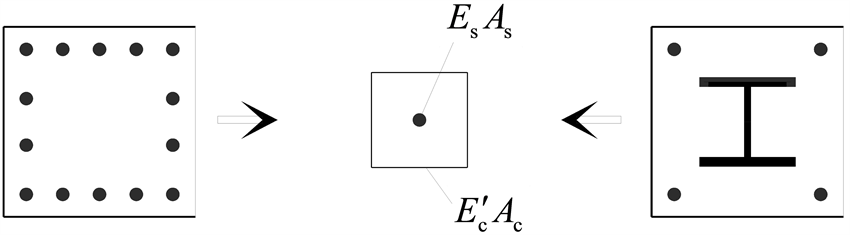
Figure 4. Simplified diagram of section steel arrangement
图4. 截面配钢简化图
按照徐变微分本构关系,有
(9)
其中,混凝土重分布轴力Ncr与钢重分布轴力Nsr是一对相互作用力,
,混凝土徐变前轴力
,钢徐变前轴力
,配钢系数
。
按照定解条件(
,
)得
(10)
混凝土徐变后轴力
,则有
(11)
又,弹性模量折减系数
(12)
则,反映配钢影响的徐变调整系数为
(13)
3.2. 变量荷载的情况
考虑荷载单调递增变化(式(3)),式(7)改写为
(14)
混凝土徐变后轴力
(15)
则,考虑配钢、荷载单调递增变化两个因素之后的徐变调整系数为
(16)
4. 算例
已知某混凝土柱,截面40 cm × 40 cm,徐变系数为2。混凝土弹性模量Ec = 3 × 104 N/mm2,钢弹性模量Es = 2.1 × 105 N/mm2。考虑滞后弹性应变,修正后弹性模量
,修正后徐变系数
。考虑配钢筋(8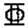 25, As = 39.27 cm2)和配型钢(HW-250 × 250 × 9 × 14, As = 92.18 cm2)两种情况。
25, As = 39.27 cm2)和配型钢(HW-250 × 250 × 9 × 14, As = 92.18 cm2)两种情况。
如果不考虑配钢,常量荷载情况的弹性模量折减系数为0.47 (按照式(4)计算),变量荷载为0.64 (按照式(8)计算)。考虑配钢,从表1知弹性模量折减系数均小于0.5,变量荷载工况、含钢率大情况折减更为显著。
对应ψ和γ,常量荷载与变量荷载相差较大,如果按照常量荷载得到的ψ和γ计算,会低估徐变影响,结果偏于不安全。因此在徐变换算弹性模量进一步简化中,须考虑变量荷载和配钢的影响。
5. 结语
结构中混凝土应力随着时间变化差异大,而徐变系数模型基于的是常应力徐变实验,有效模量法假定也是常量荷载工况。而结构中混凝土应力随着时间变化较大,尤其是预应力混凝土结构按照常量荷载工况偏差较大。另外,钢和混凝土具有不同的流变力学弹性,钢符合胡克定律,混凝土除了弹性应变,还有随着时间变化的徐变和收缩,结果将产生随时间变化的应力和变形。因此,在有效模量法的基础上进一步考虑变量荷载和配钢的影响,推导了修正后的弹性模量公式。相比现有弹性模量直接折减一半方法或者有效模量法,考虑了配钢和变量荷载工况,补充了一种更为精确的简化计算方法。
将滞后弹性应变从徐变中剥离出来,与瞬时弹性应变合并考虑,与试验结果吻合,修正之后按照徐变微分本构推导了徐变换算弹性模量设计参数(ψ, γ)的计算式。计算结果表明对于轴向徐变,不考虑配钢和变量荷载,结果偏于不安全。
基金项目
国家自然科学基金地区科学基金项目“预应力连续组合梁收缩徐变效应的计算方法研究”(项目编号:51868034)。
NOTES
*通讯作者。